19
A Weekend to Remember
Weekends don’t count unless you spend them doing something completely pointless.
—Bill Watterson
Programming constructs and algorithmic paradigms covered in this puzzle: Graph representation using dictionaries. Recursive depth-first graph traversal.
You have gotten into trouble with some of your, shall we say, difficult friends because they have realized they are not being invited to your house parties. So you announce you are going to have dinners on two consecutive nights, Friday and Saturday, and every one of your friends will be invited on exactly one of those days. You are still worried about pairs of your friends who intensely dislike each other, and you want to invite them to different days.
To summarize:
- Each of your friends must attend exactly one of the two dinners.
- If A dislikes B or B dislikes A, they cannot both be in the same dinner party.
Now, you are a bit worried because you don’t know if you can pull this off. If you had a small social circle like the following example, it would be easy. Recall that in this graph, the vertices are friends, and an edge between a pair of vertices mean that the two friends dislike each other and cannot be invited to the same party.

For dinner 1 you could invite Bob, Don, and Cleo. And for dinner 2 you could invite Alice and Eve. There are other possibilities as well. Unfortunately, that social circle was from many moons ago, and you have moved on. Your social circle now looks like this:

Can you invite all your friends A through I above, following your self-imposed rules? Or will you have to go back on your word, and not invite someone?
You’re hosed. If you look at the graph carefully, you will see that you have three friends F, G, and H, each of whom can’t be invited with the other two. You will need three separate days to host each of them.
Okay, let’s say you convince G and H not to cause a ruckus if they see each other. So your social graph now looks like this.

What about now?
Finding a Partition
With some work, you probably figured out that you could invite B, D, G, H, and I to dinner 1, and A, C, E, and F to dinner 2. Phew!
Your social circle is volatile, and you might have to do this analysis week after week. You would like to quickly know if you can make an announcement any given week, such as “party on both nights, everyone gets to come to exactly one,” with confidence that it will be a boisterous but friendly weekend. You want to write a program to check if there is some way you can “partition” (i.e., split) your friends across two nights, so that if you look at the social circle graph, all the dislike edges will be across the partition, and none within either side.
The partition we found looks like this.

This is simply a redrawing of your social circle graph. It turns out the graph above has a name—it is a bipartite graph. A bipartite graph is a graph whose vertices can be divided into two independent sets, U and V, such that every edge (u, v) either connects a vertex from U to V or a vertex from V to U. We can also say that no edge connects vertices of the same set. In the above example, U = {A, C, E, F} and V = {B, D, G, H, I}.
A graph is bipartite if it can be colored using two colors, such that no two vertices that are adjacent (i.e., share an edge) have the same color. This is, of course, a restatement of our original problem, with colors substituted for dinner nights. We will sometimes refer to the coloring constraint as the adjacency constraint.
You might think that a bipartite graph can’t have cycles. It is possible to color a graph with cycles comprising an even number of vertices using two colors: Shaded and Hatched. For example, see the graph below.

U = {A, C, E} and V = {B, D, F}, and we can invite members of U on one day, and members of V on the second. However, it is not possible to color a graph with two colors if it has a cycle involving an odd number of vertices. Consider F, G, and H in our second example, which has nine vertices. There, G and H have an edge between them. F, G, and H are in a 3-cycle, so that graph is not bipartite. The 5-cycle in the graph below renders it non-bipartite.
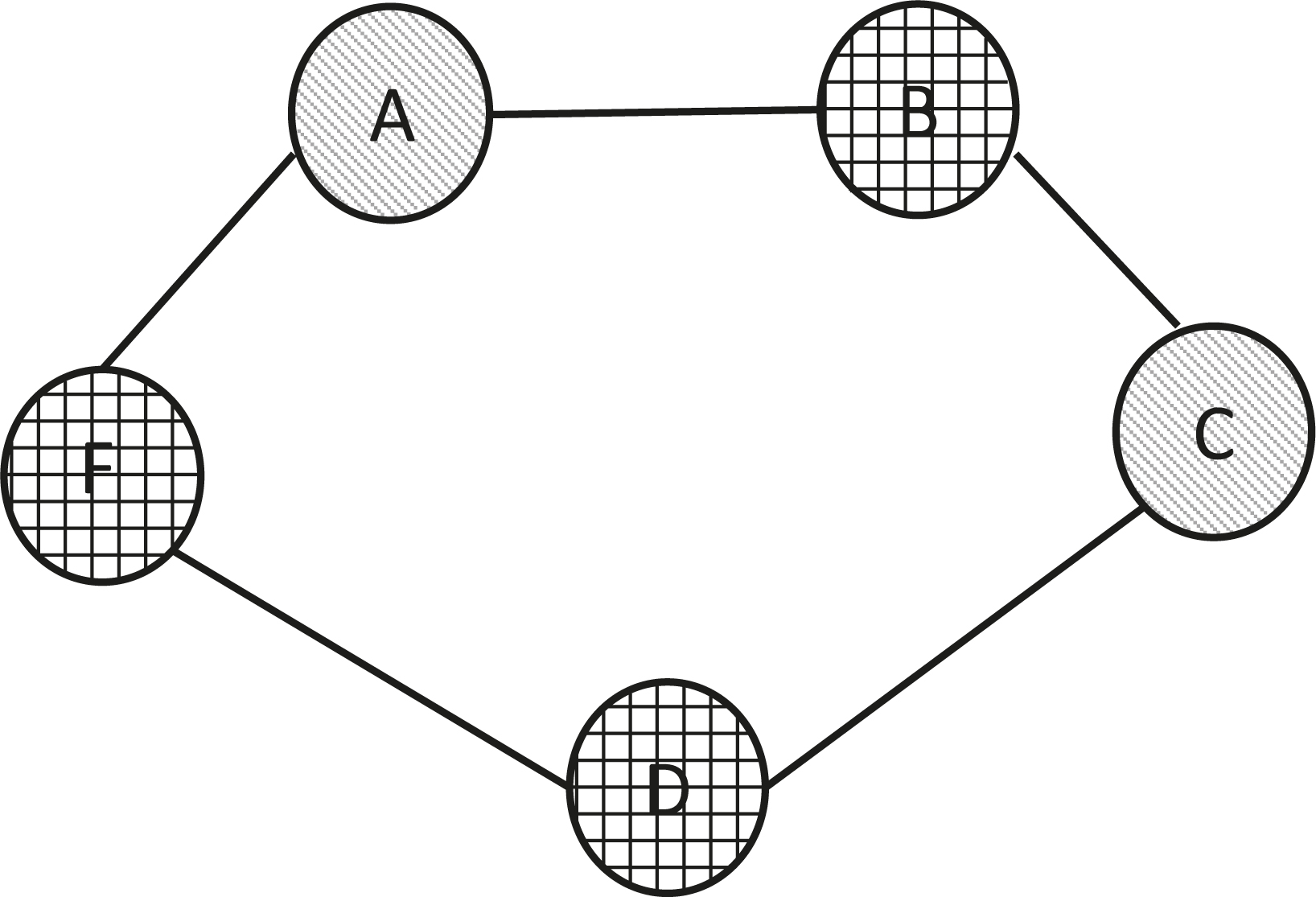
Changing the color of A to Hatched is not going to help. B and F need to be Shaded, and then C and D need to be Hatched, which violates an adjacency constraint.
Checking If a Graph Is Bipartite
We need an algorithm that successfully colors a graph’s vertices with two colors, obeying the adjacency constraint if the graph is bipartite, or telling us that the graph is not bipartite. One color will correspond to the set U, and the other to the set V. Here’s a possible algorithm that uses a technique called depth-first search.
- color = Shaded, vertex = starting vertex w.
- If w has not yet been colored, color vertex w with color.
- If w has already been colored with a different color than color, the graph is not bipartite. Return False.
- If w has already been colored with the correct color, return True and the (unmodified) coloring.
- Flip color: Shaded to Hatched, or Hatched to Shaded.
- For each neighbor v of w, recursively call the procedure with v and color (i.e., go to step 2 with w = v). If any of the recursive calls return False, then return False.
- The graph is bipartite. Return True and return the coloring.
Let’s run this algorithm on an example graph (shown below), beginning with coloring vertex B Shaded. C is the only vertex connected to B and is colored next. From C we go to D, since B is already colored. Once we color D, since C is already colored, we have the choice of coloring E or F, and we color E first.

Since E has no neighbors other than D, we next move to F, which is a neighbor of D. We color the neighbors of F in the order G, H, I (see the following graph).

You may have noticed that our example above omitted vertex/friend A, which was in the social circle we presented earlier. This is because A is not connected to any of the other vertices—it does not have any neighbors. Of course, A could be colored either Shaded or Hatched.
We’ll assume our input graph is such that we can reach all vertices from a specified start vertex. One exercise at the end of the puzzle chapter will deal with the general case of possibly disconnected components in the input graph.
Graph Representation
Before we dive into coding the algorithm, we have to choose a data structure for our graph. The data structure should allow us to perform the operations we need for the algorithm: Take a vertex, find its neighbors, then the neighbors’ neighbors, and so on. Here’s a graph representation, based on Python dictionaries, that will serve our needs. It represents the graph we just looked at.
graph = {'B': ['C'],
'C': ['B', 'D'],
'D': ['C', 'E', 'F'],
'E': ['D'],
'F': ['D', 'G', 'H', 'I'],
'G': ['F'],
'H': ['F'],
'I': ['F']}
The dictionary represents graph vertices and edges. We use strings to represent graph vertices: B in the graph picture is 'B', and so on. Each of the vertices is a key in the dictionary graph. Each line corresponds to a key-value pair, where the value is a list of edges from the vertex key. The edge is simply represented by the destination vertex of the edge. In our example, B has a single edge to C, and thus we have a single-item list for the value of the 'B' key. On the other hand, vertex key 'F' has a four-item list corresponding to its four edges.
We have undirected graphs in this puzzle, meaning that each edge is undirected. This means that if we can traverse an edge from vertex B to vertex C, we can traverse the edge in the opposite direction, from vertex C to vertex B. For our dictionary representation, this means that if a vertex key X has a vertex Y in its value list, then vertex key Y will also have vertex X in its value list. Check the dictionary graph above for this symmetry condition.
You have seen dictionaries in our anagram problem of puzzle 17 and the coin row problem of puzzle 18. They are essentially lists with more general indices that can be strings, as they are in graph. Here, we will use a few other operations on dictionaries that show you how powerful dictionaries are.
It is important to note that we do not want to depend on any particular order of the keys in the dictionary. The code we write should discover that the following graph representation graph2 corresponds to a bipartite graph, and color it properly. If we start with the same vertex and color for input graph and graph2, we should get the exact same coloring.
graph2 = {'F': ['D', 'G', 'H’, ‘I’],
'B': ['C'],
'D': ['C', 'E', 'F'],
'E': ['D'],
'H': ['F'],
'C': [‘B’, 'D'],
'G': ['F'],
'I': ['F']}
The execution of the algorithm shown in the eight diagrams above corresponds to either dictionary graph or graph2. The order in which vertices are colored does depend on the ordering of the value lists. This is why, for example, after vertex D is colored, G is colored before H, which is colored before I.
The code for bipartite graph coloring, below, closely follows the pseudocode presented earlier.
1. def bipartiteGraphColor(graph, start, coloring, color):
2. if not start in graph:
3. return False, {}
4. if not start in coloring:
5. coloring[start] = color
6. elif coloring[start] != color:
7. return False, {}
8. else:
9. return True, coloring
10. if color == 'Sha':
11. newcolor = 'Hat'
12. else:
13. newcolor = 'Sha'
14. for vertex in graph[start]:
15. val, coloring = bipartiteGraphColor(graph,\
15a. vertex, coloring, newcolor)
16. if val == False:
17. return False, {}
18. return True, coloring
The arguments to the procedure are the input graph (represented as a dictionary), the vertex start that we will color first, another dictionary coloring that stores the mapping from vertices to colors, and finally, the color that we will apply to the start vertex (color).
On line 2 we check that the dictionary graph has the vertex key start in it, and if not, we return False. Note that it is possible that during the recursive search, we encounter a vertex 'Z' in the neighbor list of a vertex, but 'Z' does not exist in the graph representation as a key. Here’s a simple example:
dangling = {'A': ['B', 'C'],
'B': ['A', 'Z'],
'C': ['A']}
Line 2 checks for cases like the one above.
Lines 4–9 correspond to steps 2–4 of the algorithm. If this is the first time we are encountering this vertex start, the dictionary coloring will not have the vertex in it. In this case, we color the vertex with color and add it to the dictionary (step 2). If the dictionary already has start in it, then we have to compare the existing color of the vertex with the color we would like to give it. If the colors are different, the graph is not bipartite and we return False (step 3). Otherwise, thus far the graph is bipartite (we might discover it is not later). We therefore return, for this call, True and the current coloring (step 4).
Lines 10–13 flip the color in preparation for the recursive calls. We represent Shaded as 'Sha' and Hatched as 'Hat'. On line 14, we iterate through the vertices in graph[start], which returns the list of neighbors of start. Line 15 makes the recursive calls for each neighbor vertex, updated coloring, and the flipped color. If any of the calls returns False, the graph is not bipartite, and we return False. If all the recursive calls return True, we return True and the coloring.
If we run:
bipartiteGraphColor(graph, 'B', {}, 'Sha')
This corresponds to the start vertex B, an empty coloring, and the color Shaded chosen for vertex B. It returns:
(True, {'C': 'Hat', 'B': 'Sha', 'E': 'Hat', 'D': 'Sha', 'H': 'Sha', 'I': 'Sha', 'G': 'Sha', 'F': 'Hat'})
The coloring is returned as a dictionary, and the order of keys in the dictionary is computer-platform-specific and run-specific, meaning that it may change if you run the program again with the same input. Even though vertex B is colored first, the key associated with vertex C appears first. Dictionaries make no guarantees that keys that are inserted first appear first when you print the dictionary, or when you generate all the keys using dictname.keys() for dictionary dictname. For example, our dictionary graph has 'B' listed first in the representation. If we print graph.keys(), which returns a list, we could get ['C', 'B', 'E', 'D', 'G', 'F', 'I', 'H']. Similarly, graph.values() generates all the values in the dictionary, which could produce [['B', 'D'], ['C'], ['D'], ['C', 'E', 'F'], ['F'], ['D', 'G', 'H', 'I'], ['F'], ['F']].
Graph Coloring
A coloring of a graph using at most k colors is called a (proper) k-coloring. While we have shown an efficient way of checking whether a graph can be colored using two colors, the same problem for three colors is a hard problem. That is, any known algorithm that can do this (correctly determine whether an arbitrary graph can be colored using at most three colors) could require, for some graphs, a number of operations that grows exponentially in the number of vertices in the graph.
The first results about graph coloring dealt almost exclusively with a special class of graphs called planar graphs, which arise from the coloring of maps. A planar graph is a graph that can be drawn so that no edges cross each other. Below is an example of a planar and a non-planar graph.
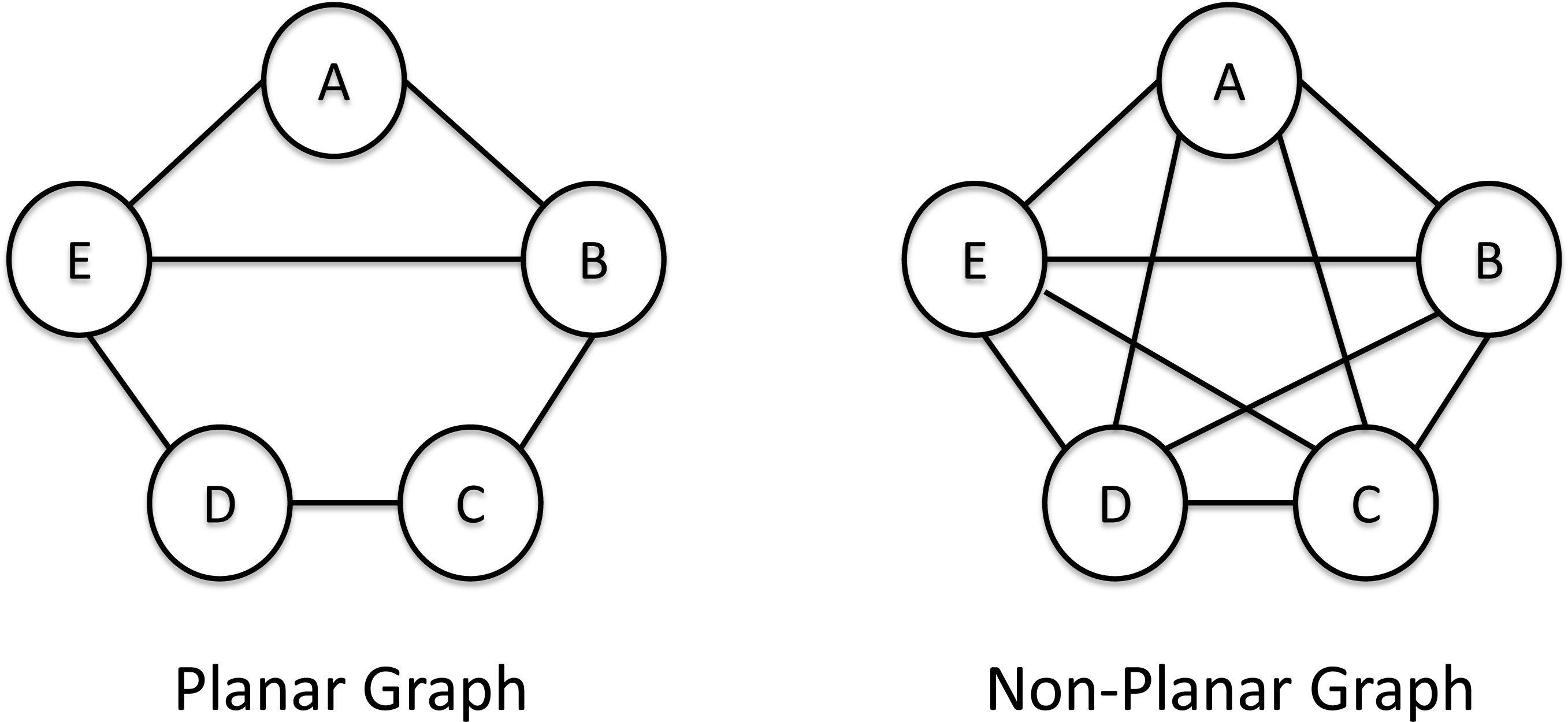
While trying to color a map of the counties of England, Francis Guthrie conjectured that four colors were sufficient to color any map so that no regions sharing a common border received the same color. This is famously called the four-color conjecture for planar graphs.
In 1879, Alfred Kempe published a paper that claimed to establish the result. In 1890, Percy John Heawood pointed out that Kempe’s argument was wrong and also proved the five-color theorem using the ideas of Kempe. The five-color theorem shows that every planar map can be colored with no more than five colors. After many attempts, the four-color theorem for planar graphs was finally proved in 1976 by Kenneth Appel and Wolfgang Haken using techniques very different from Kempe’s. The proof of the four-color theorem is also noteworthy for being the first major computer-aided proof.
Exercises
Exercise 1: The bipartite graph checker assumes that the graph is connected. Your social circle may contain disconnected components, as in the following example—a variant of the earlier example.

Modify the code so it works on the above type of graph. The current code will only color two vertices A and B in the graph if the start vertex argument to bipartiteGraphColor is A or B, and will leave C through I uncolored.
Create a parent procedure that invokes bipartiteGraphColor on the input graph with some starting vertex. Then check that all vertices in the input graph are colored. If not, begin with an uncolored vertex and run bipartiteGraphColor starting with this vertex. Continue till all vertices in the input graph are colored. Once you have colored all the vertices in each of the components, output dinner invitations, provided all the components are bipartite.
Exercise 2: Modify the procedure bipartiteGraphColor so it prints a cyclic path from the start vertex that cannot be colored using two colors, if such a path exists. Such a path will exist if the graph is not bipartite, and will not otherwise. The cycle may not include the start vertex, but will be reachable from the start vertex in the case where the graph is not bipartite. Suppose you are given the graph below:
graphc = {'A': ['B', 'D' 'C'],
'B': ['C', 'A', 'B'],
'C': ['D', 'B', 'A'],
'D': ['A', 'C', 'B']}
Your modified procedure should output:
Here is a cyclic path that cannot be colored ['A', 'B', 'C', 'D', 'B']
(False, {})
Exercise 3: The procedure bipartiteGraphColor embodies depth-first search. The code below makes recursive calls following a sequence of vertices.
14. for vertex in graph[start]:
15. val, coloring = bipartiteGraphColor(graph,\
15a. vertex, coloring, newcolor)
Rather than coloring the graph, suppose we wish to find paths between pairs of vertices. Write a function findPath that finds and returns a path from a start vertex to an end vertex if such a path exists, and returns None if it does not. If we run findPath on the dictionary graph, with start vertex 'B' and end vertex 'I', it should find the path ['B', 'C', 'D', 'F', 'I'].
Puzzle Exercise 4: A vertex in an undirected connected graph is an articulation point if removing it (and edges through it) disconnects the graph. Articulation points are useful for designing reliable networks because they represent vulnerabilities in a connected network—single points whose failure would split the network into two or more disconnected components. Below are graphs whose articulation points are shaded.

Design and code an algorithm that will determine whether a given graph has an articulation point or points, and report all such vertices if they exist.