Foreword

Sanjoy K. Mitter

The first edition of Norbert Wiener’s book, Cybernetics, or Control and Communication in the Animal and the Machine, was published in 1948. Interestingly enough, so was Claude Shannon’s seminal paper, “A Mathematical Theory of Communication.”1 William Shockley’s paper on the transistor followed in 1949.2 These texts, combined with Alan Turing’s “On Computable Numbers, with an Application to the Entscheidungsproblem” (1937) and the work of John von Neumann (e.g., his 1958 book, The Computer and the Brain), comprise the foundations of the Information Revolution, with the invention of the transistor forming the technological foundation of this revolution.3 Cybernetics is concerned with the role that the concept of information plays in the sciences of communication, control, and statistical mechanics. It is at once philosophical and technical, the contrasting points of view interspersed throughout the book. Thus, the first chapter is centered on Newtonian and Bergsonian time, which plays a role in the evolution of physics from Newtonian physics to statistical mechanics, reversibility to irreversibility, and finally to quantum mechanics. It ends with a discussion of machines in the modern age. Wiener suggests that there should be an identification of theory of automata with that of the nervous system:

To sum up: the many automata of the present age are coupled to the outside world both for the reception of impressions and for the performance of actions. They contain sense organs, effectors, and the equivalent of a nervous system to integrate the transfer of information from the one to the other. They lend themselves very well to description in physiological terms. It is scarcely a miracle that they can be subsumed under one theory with the mechanisms of physiology.4

Chapter VIII, “Information, Language, and Society,” provides a discussion of the potential of Wiener’s ideas on communication and control to social sciences, and offers a word of caution.

I mention this matter because of the considerable, and I think false, hopes which some of my friends have built for the social efficacy of whatever new ways of thinking this book may contain. They are certain that our control over our material environment has far outgrown our control over our social environment and our understanding thereof. Therefore, they consider that the main task of the immediate future is to extend to the fields of anthropology, of sociology, of economics, the methods of the natural sciences, in the hope of achieving a like measure of success in the social fields. From believing this necessary, they come to believe it possible. In this, I maintain, they show an excessive optimism, and a misunderstanding of the nature of all scientific achievement.5

Wiener was broadly interested in the informational aspects of the field of communication as well as its relationship to control, computation, and the study of the nervous system, in contrast to Shannon’s probabilistic definition of communication, which is defined in his 1948 paper cited earlier (figure 0.1). Shannon introduces the concept of mutual information and defines the concept of channel capacity as maximizing the mutual information between the input and output to the channel. Mutual information, expressed as

Figure 0.1

Shannon’s model of a communication system.

Source: Based on Claude E. Shannon, “A Mathematical Theory of Communication,” Bell System Technical Journal 27, no. 3 (July–October 1948): 381, figure 1.

is a measure of the average probabilistic dependence between two random variables. The main result is Shannon’s noisy-channel coding theorem, which states that if the message is transmitted through coding at a rate lower than the capacity of the channel, then there exists a coding scheme and a method of decoding the channel’s output such that the probability of error can be made to tend to zero, provided the coder-decoder is permitted to have infinite delay. If transmission is at a rate below capacity, however, no such coding-decoding scheme exists. This result is asymptotic and akin to proceeding toward a thermodynamic limit in statistical mechanics. The concept of entropy enters Shannon’s work in relation to compressing data without losing information by means of the source coding theorem. Thus, Wiener’s interests in the science of communication are broad and Shannon’s narrower.

Wiener made seminal contributions to the field of mathematics. His fundamental work on the definition of Brownian motion established a probability measure, the Wiener measure, on the space of trajectories. The Wiener measure plays an important role in modern theories of filtering and stochastic control, stochastic finance, and, indeed, in any physical situation where the net effect of a huge number of tiny contributions from naturally independent sources is observed.6 This theory plays an important role in the main technical part of the book: chapter III, “Time Series, Information, and Communication,” which is concerned with the problems of optimal filtering and predication of signals from noisy observation and the information-theoretic connections between the two. Among his other contributions, let me cite Wiener’s work on generalized harmonic analysis, which forms the basis of Wiener’s work on linear filtering and prediction.7 It is called generalized harmonic analysis since this theory would handle both periodic phenomena and signals composed of a continuum of frequencies.

Wiener was interested in defining the concept of information and the fundamental role it plays in communication, control, and statistical mechanics, both conceptually and mathematically. His views are captured in the introduction to the second edition of Cybernetics:

In doing this, we have made of communication engineering design a statistical science, a branch of statistical mechanics. ... The notion of the amount of information attaches itself very naturally to a classical notion in statistical mechanics: that of entropy. Just as the amount of information in a system is a measure of its degree of organization, so the entropy of a system is a measure of its degree of disorganization; and the one is simply the negative of the other.8

Wiener’s definition of information was in terms of the concept of entropy. The entropy of a discrete random variable P is given by

and by

for a continuous random variable with density p(x). Note that Wiener uses a + sign—entropy is a measure of order, hence Wiener’s definition. This is studied in the context of the problem of communication, that is, recovering the information contained in the message corrupted by noise. The message as well as the noise are both modeled as a stationary time series. Brownian motion, or white noise, plays an important part as a building block in the modeling of the message and measurement as stationary time series.

Wiener Filtering

Consider the problem of estimating a stochastic process Z(·) at time t given noisy observation

(0.1)

by using a time-invariant linear filter h(·), such that

(0.2)

and

(0.3)

is a minimum.

Let Z(·) and v(r) be a zero-mean jointly stationary stochastic process. It can be shown that the optimum filter satisfies

and that φ_zy and φ_yy are cross-correlation and autocorrelation functions. Taking Fourier transforms, and assuming signal and noise are uncorrelated, we get

When the observations y(·) are restricted to the past and the noise is white with covariance R, we have to solve the Wiener–Hopf equation

The solution of the Wiener–Hopf equation is given by

where ψ(ω) is the canonical factor of Φ_zz(ω).

The ideas presented here relate to the development of chapter III of this book, notably equations (3.914) and (3.915), which represent the mean-square filtering error. An expression for the total amount of information in the message is given in equations (3.921) and (3.922). For a modern treatment of the additive white Gaussian channel with or without feedback, the main computation is the mutual information between the message and the received signal.9

As mentioned earlier, Wiener made fundamental contributions to the theory of Brownian motion and, indeed, provided the rigorous definition of the Wiener measure. Together with Paley, he gave a definition of stochastic integration of a deterministic function. The theory of Markov processes and their connections to partial differential equations were well understood through the work of Kolmogorov and Feller.10 The theory of stochastic differential equations was developed by Ito in 1944 in his fundamental paper. These developments must have been known to Wiener. Surprisingly, Wiener did not use any of these developments in his work on filtering and prediction. It was left to R. E. Kalman to formulate the optimal filtering and prediction problem as a problem in the theory of Gauss–Markov processes.11 Relative to the Wiener formulation, Kalman made an assumption that the Gauss–Markov processes are finite dimensional. In terms of modeling, the signal and noise as stationary processes would be equivalent to assuming that the spectral density of the processes are rational.

For the representation of the signal as a linear function of a Gauss–Markov process (state-space representation), and linear observation in white noise,

(0.4)

the best linear estimate of the state, given the observations, can be derived

(0.5)

where is the best linear estimate given the noisy observations from the time 0 to t and P(t) is the error covariance. This is the celebrated Kalman–Bucy filter. The problem of prediction can be solved using essentially the same methods.12

Wiener and Control

Wiener also suggested that his ideas for the design of optimal filters can be applied to the design of linear control system compensators.14 Finally, these Wiener–Kalman ideas culminate in the linear quadratic Gaussian problem and in the separation theorem, the separation being between optimal filtering and optimal control.15

Wiener was interested in the concept of feedback and its effects on dynamical systems. His ideas on information feedback are particularly interesting:

Another interesting variant of feedback systems is found in the way in which we steer a car on an icy road. Our entire conduct of driving depends on a knowledge of the slipperiness of the road surface, that is, on a knowledge of the performance characteristics of the system car-road. If we wait to find this out by the ordinary performance of the system, we shall discover ourselves in a skid before we know it. We thus give to the steering wheel a succession of small, fast impulses, not enough to throw the car into a major skid but quite enough to report to our kinesthetic sense whether the car is in danger of skidding, and we regulate our method of steering accordingly.

This method of control, which we may call control by informative feedback, is not difficult to schematize into a mechanical form and may well be worthwhile employing in practice. We have a compensator for our effector, and this compensator has a characteristic which may be varied from outside. We superimpose on the incoming message a weak high-frequency input and take off the output of the effector a partial output of the same high frequency, separated from the rest of the output by an appropriate filter. We explore the amplitude-phase relations of the high-frequency output to the input in order to obtain the performance characteristics of the effector. On the basis of this, we modify in the appropriate sense the characteristics of the compensator.16

Wiener and Statistical Mechanics

Wiener’s most interesting ideas about statistical mechanics are those related to the Maxwell demon.

A very important idea in statistical mechanics is that of the Maxwell demon. ... We shall actually find that Maxwell demons in the strictest sense cannot exist in a system in equilibrium, but if we accept this from the beginning, and so not try to demonstrate it, we shall miss an admirable opportunity to learn something about entropy and about possible physical, chemical, and biological systems.

For a Maxwell demon to act, it must receive information from approaching particles concerning their velocity and point of impact on the wall. Whether these impulses involve a transfer of energy or not, they must involve a coupling of the demon and the gas. Now, the law of the increase of entropy applies to a completely isolated system but does not apply to a non-isolated part of such a system. Accordingly, the only entropy which concerns us is that of the system gas-demon, and not that of the gas alone. The gas entropy is merely one term in the total entropy of the larger system. Can we find terms involving the demon as well which contribute to this total entropy?

Most certainly we can. The demon can only act on information received, and this information, as we shall see in the next chapter, represents a negative entropy.18

Current work on the Maxwell demon and non-equilibrium statistical mechanics is very much in this spirit. Ideas about optimal control and information theory are linked to this development. A classical expression of the second law states that the maximum (average) work extractable from a system in contact with a single thermal bath cannot exceed the free-energy decrease between the system’s initial and final equilibrium states. As illustrated by Szilard’s heat engine, however, it is possible to break this bound under the assumption of additional information available to the work-extracting agent. To account for this possibility, the second law can be generalized to include transformations using feedback control. In particular, the work of Henrik Sandberg and colleagues shows that under feedback control the extracted work W must satisfy

, (0.6)

where k is Boltzmann’s constant, T is the temperature of the bath, and I_c is the so-called transfer entropy from the system to the measurement.19 Note that in equation (0.6) we have assumed there is no decrease in free energy from the initial to the final state. An explicit finite time counterpart to equation (0.6) characterizing the maximum work extractable using feedback control in terms of the transfer entropy from the system to the measurement is presented. To see this, consider the system shown in figure 0.4:

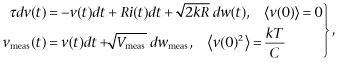(0.7)

with v(0), unit Gaussian; w and mw_meas, standard Brownian motion; w and w_meas, independent; V_meas, the intensity of the measurement noise; and τ = RC.

It can be shown that the maximum extractable work is given by

. (0.8)

Here, T_min(t) can be interpretated as the lowest achievable system temperature after t time units of continuous feedback control, assuming an initial equilibrium of T_min(0) = T. The transfer entropy, or mutual information, I_c(t) measures the amount of useful information transmitted to the controller from the partial observations:

. (0.9)

Equation (0.8) can be considered as a generalization of the second law of thermodynamics. The result in equation (0.8) uses the theory of optimal control and the separation theorem of the linear quadratic Gaussian problem.20

Wiener and Non-linear Systems

Wiener’s approach to non-linear systems is related to his work on homogeneous chaos and the representation of L² functions of Brownian motion (white noise) as an infinite sum of multiple Wiener integrals.21 In contrast to Wiener’s definition, the multiple Wiener integral as defined by Kiyosi Ito renders integrals of different orders orthogonal to each other.22 Wiener’s approach to learning views a non-linear input map in terms of the above representation, and estimates the coefficients using least-squares optimization. We can do no better than cite Wiener on this approach:

While both Professor Gabor’s methods and my own lead to the construction of non-linear transducers, they are linear to the extent that the non-linear transducer is represented with an output which is the sum of the outputs of a set of non-linear transducers with the same input. These outputs are combined with varying linear coefficients. This allows us to employ the theory of linear developments in the design and specification of the non-linear transducer. And in particular, this method allows us to obtain coefficients of the constituent elements by a least-square process. If we join this to a method of statistically averaging over the set of all inputs to our apparatus, we have essentially a branch of the theory of orthogonal development. Such a statistical basis of the theory of non-linear transducers can be obtained from an actual study of the past statistics of the inputs used in each particular case.

I ask if this is philosophically very different from what is done when a gene acts as a template to form other molecules of the same gene from an indeterminate mixture of amino and nucleic acids, or when a virus guides into its own form other molecules of the same virus out of the tissues and juices of its host. I do not in the least claim that the details of these processes are the same, but I do claim that they are philosophically very similar phenomena.23

Wiener used these ideas for the study of brain waves. It is worth pointing out that Wiener was well aware of the issues related to sampling—he analyzes the sampling theorem for stochastic inputs in chapter X, “Brain Waves and Self-Organizing Systems”:

I now wish to take up the sampling problem. For this I shall have to introduce some ideas from my previous work on integration in function space.24 With the aid of this tool, we shall be able to construct a statistical model of a continuing process with a given spectrum. While this model is not an exact replica of the process that generates brain waves, it is near enough to it to yield statistically significant information concerning the root-mean-square error to be expected in brain-wave spectra such as the one already presented in this chapter.25

Neuroscience and Artificial Intelligence

Wiener seems to have been interested in problems that continue to affect interactions between neuroscience and artificial intelligence, such as understanding the functioning of the sensorimotor system, brain–machine interfaces, and computation through neural circuits. Let me cite some of his ideas related to the vision system. Wiener emphasized that the process of recognition of an object needs to be invariant under an appropriate group of transformations, for example, the Euclidean group. He then considers the process of scanning the Euclidean group by defining a measure on the transformation group.

Voluntary movement is a result of signals transmitted through a communication channel that links the internal world in our minds to the physical world around us. What is the nature of this communication? What is “intention” in this context? These questions remain quite unanswered today.

In conclusion, Cybernetics, or Control and Communication in the Animal and the Machine attempts to create a comprehensive statistical theory of communication, control, and statistical mechanics. The book is a challenging mix of mathematics and prose, but it contains deep conceptual ideas and the patient reader will gain much from it.