Chapter 1: Basic Mathematics

Basic mathematics includes an understanding of fundamental arithmetic and algebra. Arithmetic deals with the concepts and operations of numbers, while algebra deals with the concepts and operations of symbols. Knowledge of arithmetic is essential in business, finance, and real estate. However, algebra is not always thought to be essential since many individuals are said to have succeeded in various forms of business and investment with very little knowledge of algebra. The author of this book begs to differ with that assumption. Knowledge of algebra is essential to the success of business, finance, and real estate; however, some successful individuals have relied on others to manage their affairs where such knowledge was required. In businesses and investments of all sizes and compositions, simple problems will arise that can be readily solved with the application of arithmetic operations and algebraic principles. In many instances, only a fundamental knowledge is necessary. This chapter includes a comprehensive review of basic arithmetic operations and algebraic principles.

Our number system is thought to have derived from the number of fingers on one’s hand. The term digit is derived from the Latin term digitus, which means hand. The number ten was established as the highest counting number, with additional numbers added to it. Numbers were identified as ten-and-one, ten-and-two, and so forth, which are known today as eleven, twelve, and so forth. Our number system incorporates both a real number system and an imaginary number system. The real number system includes integers, rational numbers, and irrational numbers. Integers include positive and negative whole numbers, such as -3, -2, -1, 0, 1, 2, 3. Rational numbers are any numbers that may be represented as one integer divided by another, such as 1/2, 3/4, 5/8, and so on. Irrational numbers are those numbers for which it is impossible to find any two integers that may be divided to represent it, such as � or √3. The imaginary number system is derived from taking the square root of negative numbers and is beyond the scope of this particular book.

The real number system is base ten using the digits 1, 2, 3, 4, 5, 6, 7, 8, 9, and 0. A digit is a single number. The real number system includes principles of position or place value. The value of a number depends on two factors: the particular digits used in stating it and the position of the digits when expressing it. In whole numbers, the rightmost digit indicates the unit digit and the second rightmost digit indicates tens, as shown below. Each digit’s position is assigned a value ten times greater than the one preceding it. The most commonly used digit positions are as follows:

quadrillions	hundred trillion	ten trillions	trillions	hundred billions	ten billions	billions	hundred millions	ten millions	millions	hundred thousand	ten thousands	thousands	hundreds	tens	units
8,	3	2	9,	6	9	4,	1	5	2,	8	7	0,	6	1	3

The number shown above is read: 8 quadrillion, 329 trillion, 694 billion, 152 million, 870 thousand, 6 hundred, and 13.

Arithmetic

Arithmetic is the study of numbers. The four arithmetic operations, addition, subtraction, multiplication, and division, require an understanding of whole, rational, and irrational numbers. The set of rational and irrational numbers is called decimal numbers. Before the advent of computers and calculators, various methods were developed to simplify and verify arithmetic operations with such numbers. Methods included columnar arithmetic, developing tables, casting out numbers, and the like. Today, one needs only to acquire a low cost calculator to perform such operations.

The four major arithmetic operations may be expressed as follows:

Addition	Addend + Addend = Sum
Subtraction	Minuend – Subtrahend = Difference
Multiplication	Multiplicand * Multiplier = Product
Division	Dividend ÷ Divisor = Quotient

Integer Values

Integers are the set of whole numbers which includes positive numbers and negative numbers, as well as zero. With most positive values, no symbol is used to denote that a value is positive. The positive sign of the value is implied. Most negative values, on the other hand, are denoted with a minus sign, documented in red font, enclosed in parenthesis, or denoted with some combination of the above. When dealing in monetary systems, the sign of a value is of great importance since it determines whether an amount is added or subtracted from another value. It may signify an account debit or a credit, or it may signify whether an amount has been paid or is outstanding. In the arithmetical statement, 8 + 9 = 17, the implication is +8 +9 = +17. Likewise, in the arithmetical statement, 8 – 9 = -1, the implication is +8 –9 = -1.

Factoring

The ability to factor whole numbers and to recognize those factors will assist in the understanding of many arithmetic and algebraic operations, particularly those involving fractions and the reduction of equations, which will be discussed later in this chapter. Factors of whole numbers are the exact divisors of those whole numbers. There are two types of factors: prime factors and composite factors.

Prime factors exist for prime numbers, which are numbers that are exactly divisible by only one and themselves. The prime numbers that are less than 20 include the following: 1, 2, 3, 5, 7, 11, 13, 17, and 19. These numbers are only divisible by one and by themselves. For example, 19 is only divisible by 1 and by 19.

19	= 19
1
19	= 1
19

A composite factor exists for composite numbers, which are
numbers that are exactly divisible by numbers other than one and itself. The composite numbers that are less than 20 include the following: 4, 6, 8, 9, 10, 12, 14, 15, 16, and 18. As an example, the number 18 is exactly divisible by 2, 3, 6, and 9 since the following are true:

2 * 9 = 18
2 * 3 * 3 = 18
6 * 3 = 18

Some general rules apply to factors, and they include the following:

• 2 is a factor of any even integer. The numbers 2, 4, 6, 8, 10, 12, and so on have 2 as a factor.

• 5 is a factor of any integer ending in zero or five. The numbers 5, 10, 15, 20, 25, and so on have 5 as a factor.

• 3 is a factor of any integer where the sum of the digits is exactly divisible by three.

Examples:

The number 9 has only a single digit, and it is divisible by 3. As such, 3 is a factor of 9.

The number 18 includes the two digits 1 and 8, which have a sum of 1 + 8 = 9. The sum, 9, is divisible by 3. As such, the number 18 has 3 as a factor since 6 * 3 = 18 and 2 * 3 * 3 = 18.

The number 741 includes the three digits 7, 4, and 1, which have the sum 7 + 4 + 1 = 12. The sum, 12, is divisible by 3. As such, the number 741 has 3 as a factor since 3 * 247 = 741.

• Any integer where the last digit of the integer is the same as the divisor and the other digits, from left to right, are singly exactly divisible or exactly divisible in pairs by the divisor, is itself divisible by the divisor and has the divisor as a factor.

Examples:

The number 8 is a factor of 248 since the last digit of 248 is an 8 and the other digits (from left to right), 24, are also exactly divisible by 8.

The number 7 is a factor of 63,217 since the last digit of 63,217 is a 7 and the other digits, 6321, are exactly divisible by 7, both singly and as the pairs 63 and 21. It is true that 6321 = 7 * 903. It is also true that 63 = 7 * 9 and 21 = 7 * 3.

The process of factoring numbers, like many other mathematical operations, looks more complicated than it really is. Outside practice exercises, one would not normally have to document each step of the process as is done here. The demonstrated steps are usually done in one’s head once the process is practiced and understood. With practice and one’s elementary education in multiplication and division, it should become intuitive, for example, that 6 and 3 are factors of 18.

Square Root

A square root is a more complicated form of division where the divisor is equal to the quotient. When a value is multiplied by itself, such as 5 * 5 = 25, the value is considered squared. Conversely, a square root defines the squared number. For example, the square root of 25 is 5. The square of any whole number is considered to be a perfect square.

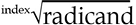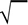The notation for square root is . The symbol is called a radical sign. When no index is specified in the notation, it indicates a square root of the radicand. If a value is specified as the index, it indicates the nth root of the radicand. If, for example, the number 3 is expressed as the index, the third root (or cubic root) is specified. The cubic root of 27, for example, is expressed as 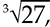since 3 * 3 * 3 = 27.

Absolute Value

Another concept that is used in arithmetic, as well as algebra, is that of an absolute value. The absolute value has application when interpreting directional numbers, such as those used in graphical methods. In most graphical methods, the number of units measured to place a point is determined relative to the origin, which is usually designated as zero. Negative numbers are then positioned in the negative direction (to the left) of the origin. Likewise, positive numbers are positioned in the positive direction (to the right) of the origin. A typical line used in graphical methods is shown below.

The number of units in any given direction is the absolute value of that number. The absolute value is expressed as two vertical bars that enclose a number. The absolute value of 4 is expressed as | 4 | and the absolute value of -4 is expressed as | -4 |. Both expressions are equal to 4.

| 4 | = 4
| -4 | = 4

Whether movement is four units from the origin in the positive direction or four units in the negative direction, the absolute number of units moved is four.

Division by Zero

Any real number may be added to, subtracted from, or multiplied by zero, but division by zero is undefined, except when zero is divided by itself. In this case:

0	= 0
0
5	= 0
0
x	= 0
0

For those who choose to automate calculations using spreadsheets or other means of digital computing, exceptions must be incorporated in the development of their chosen algorithms to avoid any division by zero. In the early days of computer programming, division by zero was cause for a variety of errors and failures, as various computer operating systems and software systems handled the division in differing ways. Some systems provided for division by zero to be set to zero; others drew a random number from somewhere in memory. In both instances, the resulting calculations were wrong. Other systems that were designed to recognize the undefined operation created a system crash, often supplemented with appropriate error messages.

Fractions

There are two basic types of fractions: common fractions and improper fractions. Fractions are expressed as follows:

numerator	= quotient
denominator

numerator ÷ denominator = quotient

Common fractions are parts of numbers that are represented as the quotient of two whole numbers, such as 1/3 and 1/8. Common fractions are also referred to as proper fractions Proper fractions are fractions in which the numerator is less than the denominator.

An improper fraction is a fraction in which the numerator is greater than the denominator, such as 11/3 or 36/9. An improper fraction may be converted to a mixed number, which is a combination of an integer and a fraction. The improper fraction 11/3 is converted to a mixed number by performing the implied division as follows:

11	= 3	2
3		3

Fractions with differing denominators cannot be added or subtracted unless they are converted to fractions with a common denominator. In such instances, the least common denominator (LCD) should be sought. The LCD is the lowest number for which all the denominators are factors. The LCD may be found by expressing each denominator in terms of its prime factors. As an example, the fractions 4/5, 5/12, 6/15, 1/18, and 7/24 are to be added. The prime factors of each of the denominators is as follows:

5	= 1 * 5
12	= 2 * 2 * 3
15	= 5 * 3
18	= 2 * 3 * 3
24	= 2 * 2 * 2 * 3

The lowest common multiple of the denominators must now be found. This implies finding the prime factors that are expressed the greatest number of times. In our example:

• 1 is expressed only once as a factor of 5.

• 2 is expressed once as a factor of 18, twice as a factor of 12, and three times as a factor of 24.

º As such, 2 is expressed the most number of times as a factor of 24.

• 3 is expressed once as a factor of 24, 15, and 12, and twice as a factor of 18.

º As such, 3 is expressed the most number of times as a factor of 18.

• 5 is expressed only once as a factor of 5 and 15.
So, 1 (1’s), 3 (2’s), 2 (3’s) and 1 (5’s) = 1 * 2 * 2 * 2 * 3 * 3 * 5 = 360.

º Thus, the LCD is 360.

This process of factoring prime numbers is another process that looks more complicated than it really is. Again, with practice and knowledge of multiplication and division, the process of factoring a value becomes intuitive.

Common Denominators

A common denominator may always be found by multiplying all the denominators together, but this may not result in the LCD. The operative word is “least.” A common denominator for 2/6 and 3/9 may be found by multiplying the denominators, 6 * 9 = 54. Though 54 is a common denominator, it is not the LCD. The prime factors of the denominators provide the LCD. The prime factors of 6 and 9 are as follows:

6	= 2 * 3
9	= 3 * 3

Since 1 (2’s) and 2 (3’s) implies 2 * 3 * 3 = 18, the LCD is 18.

The ability to determine the common denominator of fractional numbers is also necessary for comparing fractional numbers. One may find it difficult to determine if 7/16 is greater than 5/12 until both fractions are expressed with a common denominator. When both fractions share a common denominator, the numerators may then be used to determine which fractional number is greater. As an example, the values 7/16 and 5/12 have a LCD of 48, such that

7	=	21
16		48
5	=	20
12		48

It is clear from the conversion that 7/16 is greater than 5/12 since 21 is greater than 20.

Rules for Addition and Subtraction of Fractions

The addition and subtraction of common fractions should follow these simple rules:

• Express the fractions with a common denominator, preferably the LCD.

• Add or subtract the numerators.

• Convert the resulting sum or difference to lowest terms.

Example:

	2	–	1
	3		4
=	8	–	3
	12		12
	=	8 - 3
		12
	=	5
		12

Addition and Subtraction of Mixed Number Fractions

Rules for the addition and subtraction of mixed number fractions are as follows:

• Add or subtract the integer portions of the mixed numbers.

• Add or subtract the fractional portions of the mixed numbers following the rules outlined above.

• Combine the sums or differences.

• In subtraction, if the minuend is less than the subtrahend, 1 must be subtracted from the integer part of the minuend and added to the fractional part of the minuend to form a new, yet equal, statement.

Example:

In the statement 27 – 22(11/16), 27 is an integer with fractional part = 0/0. As such, the fractional part of the minuend is 0 and the fractional part of the subtrahend is 11/16. Since there is no fractional part of the minuend, one must be taken from the integer part of the minuend and added to the fractional part as follows:

27	=	27	0	=	26	16
			0			16

A new statement is formed and solved as follows:

	27	–	22	11
				16
=	26	16	–	22	11
		16			16
=	26	–	22	+	16	–	11
					16		16
=	4	+	5
			16
=	4	5
		16

Rules for Multiplication of Fractions

Multiplication involving common fractions may include multiplying an integer by a fraction (or vice versa) or multiplying a fraction by a fraction. In the multiplication of an integer by a fraction, or vice versa, the integer value should be converted into a fraction before completing the operation. After the fractional numbers are expressed, the numerators should be multiplied together and the denominators should be multiplied together to form a new fraction. The new fraction should then be reduced to the lowest terms.

Example:

The product of 5 * 3/4 is solved by first converting the integer into a fraction as follows:

5 = 5/1

A new statement is then formed and solved as follows:

	5	*	3
	1		4
=	5	*	3
	1	*	4
=	15
	4
=	3	3
		4

In the multiplication of common fractions, factors common to both the numerators and denominators may be sought to create cancellation and simplify the multiplication process. Numerators and denominators should be reduced to prime factors to create candidates for cancellation as follows:

7	*	9	*	4
12		16		21
=	7 * 9 * 4
	12 * 16 * 21
=	7 * 1 * 3 * 3 * 2 * 2
	3 * 2 * 2 * 2 * 2 * 2 * 2 * 7 * 3
=	1
	2 * 2 * 2 * 2
=	1
	16

Multiplication of Mixed Number Fractions

Rules for the multiplication of fractions when one of the fractions is a mixed number may be accomplished by one of two methods.

Method 1:

• Convert the mixed numbers to improper fractions.

• Multiply the resulting fractions.

Example 1:

The product of 48(1/2) * 3(2/3) is found as follows:

Convert the mixed numbers to improper fractions:

48(1/2) = 97/2 and 3(2/3) = 11/3

So,

	97	*	11
	2		3
=	97 * 11
	2 * 3
=	1067
	6
=	177	5
		6

Method 2:

• Multiply the integer part of the first value by the integer part of the second value, if one exists.

• Multiply the integer part of the first value by the fractional part of the second value, if it exists.

• Multiply the fractional part of the first value by the integer part of the second value, if it exists.

• Multiply the fractional part of the first value by the fractional part of the second value, if it exists.

• Add the partial products.

Example 2:

Using the same example as above, 48(1/2) * 3(2/3), the product is found as follows:

48	*	3	+	48	2	+	3	1	+	1	*	2
					3			2		2		3
=	144	+	32	+	3	+	2
					2		6

The rules for addition of mixed number fractions is used to find the sum of the partial products. Since 6 is the LCD of the fractional partial products, the sum becomes:

144	+	32	+	9	+	2
				6		6
=	176	+	9 + 2
				6
=	176	+	11
			6
=	176	+	1	5
				6
=	177	5
		6

Rules for Division of Fractions

In the multiplication of common fractions, it is understood that

	8	*	1
			2
=	8	*	1
	1	*	2
=	8
	2
=	4

The fraction 1/2 is the reciprocal of 2. The reciprocal of a number is 1 divided by that number. As such, the product of a number and its reciprocal is always equal to one. The product of 8 and its reciprocal is one.

8	*	1	=	1
		8

In division, the quotient obtained by dividing one number by another is equivalent to multiplying the numerator by the reciprocal of the denominator.

Example 1:

	8
	2
=	8	*	1
			2
=	8	*	1
	1	*	2
=	4

If the numerator and denominator of a fraction are interchanged, a reciprocal is formed. This interchange of terms is known as inverting a fraction. The product of multiplying a fraction by its reciprocal is always equal to one. The reciprocal of 2/8 is 8/2. The product 2/8 * 8/2 = 16/16 = 1.

The division of common fractions makes use of this method of reciprocals such that the division of common fractions involves multiplication. Division involving common fractions may include dividing an integer by a fraction (or vice versa) or dividing a fraction by a fraction. In the division of an integer by a fraction, or vice versa, the fraction should be multiplied by the reciprocal of the integer before completing the operation. The new fraction should then be reduced to the lowest terms.

Example 2:

The quotient 3/4 ÷ 5 is solved by first converting the integer into its reciprocal as follows:

The reciprocal of 5 is 1/5.

A new statement is then formed and solved as follows:

	3	*	1
	4		5
=	3	*	1
	4	*	5
=	3
	20

In the division of two fractions, the divisor must be inverted to create a multiplication operation. Inverting the divisor has the effect of creating a multiplication operation in which the dividend is multiplied by the reciprocal of the divisor.

Example 3:

The quotient of 5/6 ÷ 4/5 is solved as follows:

		5
		6
		4
		5
=	5	*	5
	6		4
=	5	*	5
	6	*	4
=	25
	24
=	1	1
		24

Division of Mixed Number Fractions

To divide fractions when one of the fractions is a mixed number, the mixed number is converted into an improper fraction and the rules for the division of common fractions are followed.

Example:

	5	1
		3
	1	3
		5
=		16
		3
		8
		5

=	16	*	5
	3		8
=	16	*	5
	3	*	8
=	80
	24
=	10
	3
=	3	1
		3

Division is the process of determining how many times one number is contained in another. If the divisor is not a factor of the dividend, the result of the division process includes a remainder. This remainder may be expressed as either a fraction of the dividend or a decimal value.

Decimals

Most calculations in business, investment, and real estate are not as reliant on integers or fractions as they are on decimal values. Integers are seldom used because integers provide poor units of measure. Integers, for example, cannot provide the precision necessary to determine whether a measured distance is 4 feet or 4.5 feet. Fractions are seldom used because fractional numbers, particularly those with large numerators or denominators, can be awkward and are best understood when converted to decimal form. A measurement is more likely to be presented as 0.0255 rather than 5/196. Prices are stated in dollar and cents, which are decimal values. Decimal values include amounts that are less than a single unit (or 1), such a fifty cents ($0.50).

When a fraction is converted to decimal form, it is considered a pure decimal. When a mixed number is converted to decimal form, it is considered a mixed decimal. The addition, subtraction, multiplication, and division of decimal numbers are carried out similarly to that of whole numbers. Care must be taken, however, to properly place the decimal point.

Decimal numbers may be presented with differing levels of accuracy so that results from one calculation may differ somewhat from other calculations, though they are in actuality the same. When accuracy is specified to a certain number of significant digits, this means that all the digits may be read directly, except the last digit. The last digit is an interpolation or rounding. In most businesses and other activities that involve money, the precision of decimal numbers is usually limited to two decimal places beyond the decimal point.

Interpolation

Interpolation is a method for estimating a value when values greater than and less than an unknown value are known. Interpolation involves proportions. The proportional units between known values must first be determined, and the interpolated value is then computed within those same proportions. It is important to remember that an interpolated value is not exact, but an estimate or approximation.

Example:

The return on five investment accounts is released every two weeks as follows:

	Account A	Account B	Account C	Account D	Account F
Week 2	16.3%	18.5%	19.5%	17.5%	16.9%
Week 4	15.8%	16.7%	17.4%	17.2%	15.9%
Week 6	15.7%	15.5%	15.0%	16.2%	15.4%
Week 8	12.4%	13.2%	14.2%	15.1%	15.3%

Between weeks 4 and 6, Account D decreased from 17.2% to 16.2%. We want to estimate the return at week 5. From the data, we know that, between weeks 4 and 6, the difference was 1%.

2	1	Week 4	17.2%	x%	1%
		Week 5
		Week 6	16.2%

The time difference between week 4 and week 5 is 1 and between week 4 and week 6 it is 2. The difference in returns between week 4 and week 5 is what we are attempting to define and the difference between week 4 and week 6 is 1%. The proportion is as follows:

1 wks	=	x%
2 wks		1%
x%	=	1%	*	1 wks
				2 wks
=	1	*	1
			2
=	1
	2
=	0.5%

Since x = 0.5%, we may either subtract 0.5% from the return for week 4 or add 0.5% to the return for week 6 to arrive at the estimated return for week 5. At week 5, the return is estimated to be:

17.2% – 0.5%
= 16.7%
or
16.2% + 0.5%
= 16.7%

The estimated return for week 5 is 16.7%.

Decimal Multiplication

In the multiplication of two decimal values, the resulting product should include the placement of the decimal point as many places to the right as there are places in the multiplicand and multiplier. In the product 38.274 * 5.43 = 207.82782, the total number of decimal places is 3 (in the multiplicand) + 2 (in the multiplier) = 5.

When multiplying a decimal value by a value that is a power of 10, such as 100 (100 = 102), the decimal point of the decimal value must be moved as many places to the right as there are zeros in the value that is a power of 10.

2.4586 * 10 = 24.586
2.4586 * 100 = 245.86
2.4586 * 1000 = 2458.6
2.4586 * 10,000 = 24,586
2.4586 * 100,000 = 245,860
2.4586 * 10,000,000 = 2,458,600

In the product of two decimal values, the decimal point may be moved the same number of places, in opposite directions, without affecting the proper calculation of the product.

Example:

The product: 18.62 * 3.8 = 70.8
and so too is the product: 186.2 * 0.38 = 70.8
and the product: 1.862 * 38 = 70.8

Decimal Division

In the division of two decimal values, the decimal point of either the divisor or dividend may be moved the same number of places, in the same direction, without affecting the proper calculation of the quotient.

Example:

The quotient: 18.62 ÷ 3.8 = 4.9
and so too is the quotient: 186.2 ÷ 38 = 4.9
and the quotient: 1.862 ÷ .38 = 4.9

Locating the decimal point in the quotient of decimal division is fundamental. If the divisor is a whole number, the decimal point should be placed as many places to the right as there are places in the dividend. If the divisor is not a whole number, the decimal point of the divisor should be moved to the right of the last digit in the divisor, and the decimal point of the dividend should be moved an equal number of places to the right. This has the effect of converting the divisor to a whole number. If the dividend does not have enough digits to accommodate the decimal placement, zeros should be added. The decimal point of the quotient is then placed as many places to the right as there are places in the dividend.

Significant Digits

Whole numbers are exact numbers, whereas decimal and fractional numbers are approximated values. No measurement or decimal value is absolutely correct. These types of approximated values are known to be correct only to some number of significant digits.

The number zero has particular importance as a significant digit. Zeros are significant digits if they occur between two nonzero digits or if the zero is the final digit to the right of a decimal point. As examples, the values 130.08 and 130.80 have 5 significant digits. A zero used to locate a decimal point is not significant. For example, the values 0.08 and 0.8 have only one significant digit.

Values have the same precision if they are given the same number of decimal places. The value 0.08 has the same precision as the value 130.08, which has 5 significant digits. The significance of a digit is dependent on the application for which it is being used. The value 2,500 may have two, three, or four significant digits if it is used as a measure of distance, but if it is used as a count of money ($2,500) it has four significant digits. Two rules apply to significant digits as follows:

• In multiplication and division, the number of significant digits in a product or quotient is the same as that in the least significant of the values used to calculate the product or quotient. As an example, the product 16 * 35.6 = 569.6, has only two significant digits since 16 is the least significant of the values used in forming the product. The product should be written 16 * 35.6 = 57. However, if it were predetermined that 16 was an integer good for an infinite number of decimal places, the product would have three significant figures based on the value 35.6. The product would be correctly written as 16 * 35.6 = 570.

• In addition and subtraction, the number of significant digits is the same as that of the least accurate value used in the calculation.

Percentages

The principles of fractions and decimals have application in real estate and other disciplines that deal with percentages. When two things are compared with one another, that comparison is oftentimes expressed as a percentage. Percent is expressed by the symbol % and is synonymous with the concept of rate.

Percentages provide another way of expressing fractional or decimal values. The percent symbol is merely a substitute for the decimal point in a decimal value or the quantity, 100, in the denominator of a fraction. As such, 75% = 0.75 = 75/100. To express a fraction as a percent, the fraction must first be converted to a decimal value by performing the required division. After the division is performed, the decimal point is moved two places to the right and the % symbol is affixed as follows:

7 ÷ 15 = 0.4666… = 46.6…% = 46.6%

The precision used in dealing with percentages is dependent upon the individual or system making use of the values. In monetary systems, precision to one or two decimal places is usually sufficient.

To convert a percent to a fraction, the % symbol must be removed and one of the following procedures must be followed. Allow the percentage to become the numerator of the fraction with a denominator of 100 or, if the percentage is expressed as a fraction, multiply the denominator by 100. Then, reduce the newly acquired fraction to its lowest terms.

Example 1:

46.6%	46.6	=	23.3
	100		50

Example 2:

2	%	=	2	=	2	=	1
3			3 * 100		300		150

There are three basic types of percentage calculations, which include finding the percentage rate, finding the percent of a number, and finding the base number when the percentage is known.

Finding the Percentage Rate

Finding the percentage rate involves finding what percent one number is of another. As an example, one may need to answer the query, 20 is what percent of 60? In other words, 20 are how many hundredths of 60? The query is answered as follows:

20 ÷ 60 = 0.333…
rounding to 2 decimal places,
0.333… = 0.33 = 33%

Finding the Percent of a Number

Finding the percent of a number equates to the multiplication of two numbers, the base number and the percentage rate. In the query, what is 20% of 60, 20% is the percentage rate and 60 is the base number. The query is answered as follows:

20% * 60 = .20 * 60 = 12.0 = 12%

Finding the Base Number

Finding the base number when the percentage and percentage rate are known involves a division operation. The percentage is divided by the percentage rate. In the query, 20 is 60% of what number, 20 is percentage and 60% is the percentage rate. The query is answered as follows:

20	=	20	=	33.3...	=	33.3
60%		.60

Common Fractional Equivalents

Fractional equivalents are used to simplify the mathematics of fractions. Some fraction equivalents are used more often in science and business than others. Some commonly used fractional equivalents are shown in Table 1.

Table 1: Common Fractional Equivalents
Fraction	Percent		Fraction	Percent		Fraction	Percent
1/8	= 12(1/2)%		1/25	= 4%		7/8	= 87(1/2)%
1/6	= 16(2/3)%		1/24	= 4(1/6)%		2/3	= 66(2/3)%
1/5	= 20%		1/18	= 5(5/9)%		3/4	= 75%
1/4	= 25%		1/16	= 6(1/4)%		5/6	= 83(1/3)%
1/3	= 33(1/3)%		1/15	= 6(2/3)%		5/12	= 41(2/3)%
1/2	= 50%		1/12	= 8(1/3)%		7/12	= 58(1/3)%
1/75	= 1(1/3)%		1/9	= 11(1/9)%		5/16	= 31(1/4)%
1/40	= 2(1/2)%		3/8	= 37(1/2)%		9/16	= 56(1/4)%
1/30	= 3(1/3)%		5/8	= 62(1/2)%

Aliquant Parts

An aliquant part is a fractional part. The equivalents shown in Table 1 are aliquant parts of 100%. If an aliquant part is known, any other aliquant part can be found by multiplying the initial aliquant part by the numerator of the new aliquant part. As an example:

If it is known that 16(2/3)% = 1/6 of 100%
then 3/6 of 100% is calculated as follows:
3 * 16(2/3)%
= 48(6/3)% = 50%

As another example: 5/24 of 100% is calculated as follows:

(5/24) = 5(1/24)

from Table 1, 1/24 is 4(1/6)% of 100%

then

5 * 4(1/6)%

= 20(5/6)%

Elementary Algebra

One of the first requisites for finding solutions to problems is the ability to express relationships in algebraic symbols. To be able to express such relationships, an understanding of the most elementary arithmetic and algebraic relationships and their significance is necessary. Various types of algebraic relationships are used in business, finance, and real estate to solve problems involving relationships between variables, percentages, proportions, discounts, rates of return, and so on.

Literals

In arithmetic, operations are performed on Arabic numbers. In algebra, letters of the alphabet replace Arabic numbers. These letters may have different numerical values assigned to them. These letters are called literal numbers or literals. Literal numbers are symbols used in algebra to represent numbers and to perform operations on those numbers. Literals make it easier to state mathematical definitions in a generalized form. The literal statement, a > b signifies that, on a number scale, the value represented by a is greater than the value represented by b. In algebra, when a literal symbol is used to represent a value that may vary, the literal symbol is known as a variable. If the literal symbol is used to represent the same value throughout a discussion or problem, the literal symbol is called a constant.

Algebraic Terms

Literal numbers, such as a, b, and c, as well as products such as 2a and 3bx, are called algebraic terms. Since 2a represents a product of 2 and a, both 2 and a are factors of 2a. These factors are called coefficients of the algebraic term. Since 2 is an Arabic numeral, it is considered a numerical coefficient of a. Since a is a literal, it is considered a literal coefficient of 2. Algebraic terms with the same literal coefficient are called like or similar terms. The algebraic terms, 4a and 24a, are considered like terms. Like terms can be added together or subtracted from one another. Unlike terms cannot.

4a + 6a – 2a = 8a
4a + 6b – 2a = 2a – 6b

Equations

When algebraic terms are combined with mathematical operators such as +, -, or >, the combination is called an algebraic expression or algebraic statement. An algebraic expression of one term is called a monomial. An algebraic statement of two terms is called a binomial. An algebraic statement of two or more terms is called a polynomial.

Monomial:	2x
Binomial:	2x + 3y
Polynomial:	2x + 3y + 4z

The algebraic statement of x + x = 2x holds true for all values assigned to x. The value of the letter x is considered to be variable. Such equality between two expressions is known as an equation. An equation that holds true for all values of a variable is called an identical equation. An equation that is true for only a certain value or an equation that is true for a specific set of values is called a conditional equation. The values are called unknowns. Any value that is substituted for the unknown in an equation reduces both sides of the equation to the same value. The substituted value is known as the root of the equation and is said to satisfy the equation. To solve an equation is to find the root of the equation that reduces both sides of the equation to the same value.

Axioms of the equality of equations are as follows:

If equals are added to equals, the sums are equal.	If a+b=x, then a+b+c=x+c
If equals are subtracted from equals, the differences are equal.	If a+b=x, then a+b-c=x-c
If equals multiply equals, the products are equal.	If a÷b=x, then (a÷b)c=xc
If equals divide equals, the quotients are equal.	If a÷b=x, then (a÷b)÷c=x÷c

Equations also follow the rule of transposition, which dictates that any term of an equation may be moved from one side of the equation to the other as long as the algebraic sign of the term is changed. The following equations are equal:

a + b = c – d
and
a + d = c – b

Monomials and Polynomials

To multiply two monomials, the product of the numerical coefficients and the product of the literal coefficients must be found. If the literal coefficients are the same, the exponent of their product is the sum of the exponents of the coefficients. Only like literal coefficients may be combined. As an example, the monomials 5x2 and 4x are to be multiplied. The process is as follows:

The numerical coefficients are multiplied: 5 * 4 = 20
The literal coefficients that are the same are multiplied:
x2 * x = x(2+1) = x3
Therefore
5x2 * 4x = 20x3

The product of a monomial and a polynomial is found by multiplying each term of the polynomial by the monomial as follows:

3ab (5ab2 + 8a2b – 4)
= 15a2b3 + 24a3b2 – 12ab

The product of two binomials is found by multiplying each term of one quantity by each term of the other and adding the results as follows:

(3x + 4y) * (3x – 4y)
= 3x * 3x + 3x * (-4y) + 4y * 3x + 4y * (-4y)
= 9x2 – 12xy + 12xy – 16y2
= 9x2 – 16 y2

This particular problem represents a common algebraic relationship: the product of the sum and difference of two numbers. This product is always equal to the square of the first number minus the square of the second number.

(x + y) * (x - y)
= x2 - y2

Another commonly used relationship is the multiplication of a sum or difference by itself. This product is called a perfect square. The products always take on the following common forms:

(x + y)2		(x - y)2
= (x + y) * (x + y)		= (x - y) * (x - y)
= x2 + 2xy + y2		= x2 - 2xy + y2

Factoring

The process of factoring involves determining the factors that are common to an algebraic expression. When examining equations to factor, the first objective is seeking common forms of equations. Some common products are specified above. In examining an equation, such as 9x2 + 6x + 1, a perfect square is recognized since the middle term is equal to twice the product of the square root of the first and third terms, i.e., 9 = 32 , 1 =12, and 6 = 2 (3 * 1). The statement represents the square of x + 1.

9x2 + 6x + 1
= (3x + 1)2

Another common algebraic relationship specifies that if every term of an algebraic expression contains a common factor, that factor may be removed to create a new expression. In the expression ax = ay, a is common to both terms of the expression, and the expression takes on the following form:

ax + ay = a (x + y)

In examining the expression, 5x2 + 10x2y – 20x2y3, it is apparent that both 5 and x2 are factors of each term of the equation, and the factor 5x2 may be factored out to create a new expression as follows:

5x2 + 10x2y – 20x2y3
= 5x2 ( 1 + 2y – 4y3 )

Solving Equations

In solving algebraic equations, words and expressions have the same meaning as they do in arithmetic. The sum of 6 and 9 may be stated algebraically as 6 + 9. Likewise, the sum of x and y may be stated as x + y. Certain ideas may be expressed easily with an algebraic equivalent. Some common equivalents are as follows:

Three more than x	x + 3
x increased by 3	x + 3
The sum of x and 3	x + 3
Three greater than x	x + 3
Three less than x	x – 3
The excess of x over 3	x – 3
x reduced by 3	x – 3
Three more than twice x	3 + 2x
3 more than one-half of x	½x + 3
3 less than twice the product of x and y	2xy – 3
The sum of x and y	x + y
The sum of x and y, squared	(x + y)2
The sum of squares of x and y	x2 + y2
The value of x in pennies	0.01x
The value of x apples at y cents per apple	0.01xy
The value of x bags of apples at $2 per bag	$2x

After an appropriate algebraic equation is defined, the equation must then be solved. In business, if a problem occurs frequently with variation only in the numbers used, the most time saving method of solving the problem is to develop a chart of possible solutions. The method may be used by anyone whether or not they understand how the computations for the chart were derived. Charts showing sales taxes, income taxes, logarithms, and other data unique to a need have been developed for use. This method of charting data precludes that all possible solutions are accounted for. Usually this is not the case. A better alternative method for solving these problems involves developing an equation that properly defines the problem and allows one to calculate solutions.

Equations Versus Formulas

A formula is any statement of principle or rule involving magnitudes, expressed in the form of an equation. A formula may be solved for any given unknown; however, formulas often contain operations that cannot be fully carried out. When no particular value is assigned to unknown quantities, a formula cannot be solved.

The relationship between the base (B), rate (R), and percent (P) in percent problems may be stated algebraically as the formula, BR = P. This formula may be easily solved for any of the three unknowns as follows:

B = R/P

R = P/B

P = BR

An amount A is defined by the relationship A = B + P. The formula for A could then be devised as follows:

A = B + P
Since P = BR, then
A = B + BR
A = B (1 + R)
and,

B	=	A
		1+R

Though a valid formula is established, the mathematical operations cannot be carried out until values are assigned to the unknown variables of the formula.

Laws of Algebra

The fundamental laws of algebra include the cumulative, associative, and distributive laws. The commutative law applies to addition and multiplication. This laws dictates that it does not matter in which order two numbers are added or multiplied; the respective sum or product is the same. As such, 4 + 6 = 10 and 6 + 4 = 10. Likewise, 4 * 6 = 24 and 6 * 4 = 24. The associative law also applies to addition and multiplication. The associative law dictates that the sum or product of three or more numbers is the same regardless of how the numbers are grouped. As such, 2 + (4 + 6) = 12 and (2 + 4) + 6 = 12. Likewise, 2 * (4 * 6) = 48 and (2 * 4) * 6 = 48. The distributive law dictates that the product of one number and the sum of two or more other numbers is equal to the products of the number and each of the numbers of the sum. As such, 4 (3 + 5) = 4 * 3 + 4 * 5. The following literal statements are used to express the fundamental laws of algebra:

Commutative law of addition:	a + b = b + a
Commutative law of multiplication:	ab = ba
Associative law of addition	a + ( b + c) = (a + b) + c
Associative law of multiplication	a(bc) = (ab)c
Distributive law	a(b + c) = ab + ac

Laws of Signs

The laws of signs apply to all real numbers: integers, rational numbers, and irrational numbers, and govern the operations of addition, subtraction, multiplication, and division. The laws of signs are as follows:

Add two real numbers with like signs	Add their absolute values and affix the common sign.
Add two real numbers with unlike signs	Subtract the absolute value of the smaller value from the absolute value of the larger value and affix the sign of the number with the larger absolute value.
Subtract two real numbers	Change the sign of the number to be subtracted, add their absolute values, and affix the sign of the number with the larger absolute value.
Multiply or divide two real numbers with like signs	Calculate the product or quotient of their absolute values.
Multiply or divide two real numbers with unlike signs	Calculate the negative of the product or quotient of their absolute values.

Exponents

In multiplication, it is often times necessary to multiply a number by itself several times. Rather than actually expressing this redundant operation, the notation an is used, where a is the base number and n is the exponent that represents the number of times that “a” appears in a product. The expression is termed the nth power of a. The fifth power of 3 is represented as follows:

35 = 3 * 3 * 3 * 3 * 3 = 243

Certain operations with exponents are of particular importance. They include the following:

a0 = 0
a1 = a
an * am = an+m		a3 * a5 = a3+5 = a8
an ÷ am = an – m, m > 0 and a ≠ 0		a3 ÷ a5 = a3 – 5 = a-2
an ÷ am = 1 ÷ am – n, m > 0 and a ≠ 0		a3 ÷ a5 = 1÷ a5 – 3 = 1÷ a2
(an)m = anm		(a3)5 = a3*5 = a15
(ab)n = an bn		(ab)3 = a3 b3
(a ÷ b)n = an ÷ bn, b ≠ 0		(a ÷ b)3 = a3 ÷ b3

Extracting a Root

When the process of squaring a number is reversed, the process is called extracting the square root. When a value is squared, as in x2, the value of x can be found by taking the square root of x2:

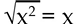
The notation 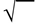indicates that the value of x may be either a positive or negative value. The arithmetic process to extract the square root of a number involves separating the number into groups of two digits, starting at the decimal point. The number of two digit groups defines the number of digits in the square root. If a number less than ten is squared, there will be only two digits to the left of the decimal point. If the number is more than ten, but less than 100, there will be two sets of two digit numbers to the left of the decimal point. The rest of the process to manually extract a square root is cumbersome and will not be detailed here. A scientific calculator provides the best method of calculating square. The partial process outlined above may be used in assessing the correctness of any digitally computed square root.

In finding the root of an exponential number, the root must divide the exponent. Since any number, a, is presumed to have an exponent of 1 (a = a1), the square root of a is:

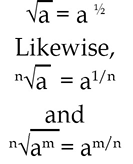
When the index (n) is greater than two, the process of extracting the roots requires the use of logarithms. The process of extracting roots using logarithms is known as evolution. Evolution involves dividing the logarithm of the number by the index of the root and then finding the antilogarithm of the quotient. The manual use of logarithms and antilogarithms in arithmetic processes is too detailed and cumbersome to present here. Such operations are more easily and accurately carried out with some method of digital computation, such as with the use of a scientific calculator or computer software.

Logarithms

A logarithm is the converse of an exponent in the same sense that addition is the converse of subtraction. A logarithm, also called the log of a number, is the exponent of a value expressed as an, where a is the base number and n is the exponent. The base may be any number, but a base of 10 is of particular importance since the logarithm of any number to base 10 can be computed using methods of computing the logarithm of numbers between 1 and 10. As such, the logarithm is the exponent to which the number 10 must be raised to express a number. The power of 10 in the expression 103 is 3, and 3 is a logarithm. For any value of the form 10x, the logarithm of 10 is x. This is expressed:

log 10x = x

Before the days of digital computing, individuals performed mathematical operations by hand and used charts and tables to document the results of the more complex and repetitive operations. In the calculation of logarithms, an apparatus known as a slide rule was used, along with tables of logarithms. Tables of logarithms are used to calculate the log of any decimal value. Since it was not practical or possible to create a table of logarithms for every single decimal value, tables were devised to provide solutions for every integer and the mantissa of every decimal value. This book will not provide a discussion of the use of slide rules or tables of logarithms since their use is outdated. However, specific properties of logarithms, including the characteristic and mantissa, will be introduced. It should be noted that tables of logarithms are available for use in the absence of digital computing methods.

Scientific Notation and Standard Position

A number is expressed in standard notation, also called scientific notation, when that number can be expressed as the product of a number between 1 and 10 and a power of 10. Since any decimal number can be expressed as the product of a number between 1 and 10 and a power of 10, any decimal number can be written in scientific notation. Any number expressed in scientific notation can also be expressed in what is called standard position. Standard position is a decimal expression where the decimal point immediately follows the first digit on the left. The decimal value 234.56 is expressed in standard position as 2.3456 * 102.

To express any number in scientific notation, move the decimal point to the standard position and multiply the resulting number by a power of 10. The exponent of 10 will be equal to the number of places the decimal point was shifted. If the decimal point is moved to the left, the exponent will be positive. If the decimal point is moved to the right, the exponent will be negative. As an example, the value .0029487 is expressed in scientific notation as 2.9487 * 10-3. When numbers are expressed in scientific notation, the same series of digits appear in the expressions. The numbers only differ in the power of 10 used.

The decimal point is understood to exist at the far right of any integer value. As such, the value 56 is understood to be 56., but the decimal point is not usually written. When converting a number to scientific notation, if the decimal point is moved only 1 place to the right, the exponent is 1. However, an exponent of 1 is often not written since any number raised to the first power is equal to itself and 101 = 10. The number 56 expressed in scientific notation is 5.6 * 101, expressed as simply 5.6 * 10.

Properties of Logarithms

Certain operations with logarithms are of importance. They include the following:

log 10a	= a log 10
log (a * b)	= log a + log b
log (a ÷ b)	= log a – log b

When the logarithm of a value is sought, the problem is interpreted as finding the exponent of a number when the number is expressed in scientific form. As such, the logarithm of 154.81 is calculated as follows:

log 154.81
converting the value to scientific form
= log (1.5481 * 102 )
= log 1.5481 * log 102
= log 1.5481 + (2 * log 10)
= log 1.5481 + (2 * 1)
= log 1.5481 + 2

Since 101 = 1 and log 10 = 1, it stands to reason that the log of any number less than 10 must be a decimal, which is a value that is less 1. Further, any value that can be expressed in standard notation can be expressed as a multiple of that decimal and an exponent applied to 10. As an example, the value .056 is less than 10 and can be expressed in standard notation as 5.6 * 10-2. The log of .056 is calculated as follows:

log .056
= log (5.6 * 10-2)
= log 5.6 * log 10-2
= log 5.6 + (-2 * log 10)
= log 5.6 + (-2 * 1)
= log 5.6 – 2

Antilogarithms

The mathematics of logarithms provides methods to compute the log of a value and, conversely, methods of determining the value itself. In the statement log .056 = 1.251811973, the value .056 corresponding to the logarithm is known as the antilogarithm of 1.251811973.

Example:

In the equation (x-a)n = b, we want to solve for n using logarithms.

log (x – a)n = log b
n log (x – a) = log b

log (x-a)	=	log b
		n
x - a =	antilog (	log b	)
		n
x = antilog (	log b	) + a
	n

Characteristic and Mantissa

It can be seen from the two examples above that a solution of a logarithm may result in two terms: a logarithm and a whole number. The term that is a whole number is called the characteristic. The characteristic is equal to the power of the number when the number is expressed in scientific form. The term that is a logarithm is called the mantissa. The mantissa is equal to the logarithm of the number between 1 and 10. In the value log (5.6 * 10-2), the characteristic is -2 and the mantissa is log 5.6. As such:

log .056
= log 5.6 – 2,
as was calculated in the example above

The purpose in converting the logarithm of a number into an expression that includes a logarithm of a number is that the logarithm in the new expression seeks the logarithm of a number whose value falls between 1 and 10. As such, the value of the logarithm can be found in a table of logarithms. A much easier method of computing logarithms is to use a calculator or other method of digital computing. The process of using a table of logarithms becomes complicated when the characteristic is negative.

In higher levels of mathematics and engineering than are presented here, logarithms and exponents have application in complex computing, particularly when the notation e is used. This book does not extend to that level of sophistication and, as such, will not delve any further into the complexities of how and why logarithms work. The important thing to know about logarithms and exponents is that they are the methods necessary to solve problems involving square and other roots. In the absence of digital computing, even a low cost scientific calculator provides more timely and accurate results than manual computations.

Linear Equations

A single equation with two unknowns is known as a linear equation. The term linear is used since the geometry of lines dictates that any line can be defined by at least two points .The value of one unknown can be stated in terms of the other unknown. As an example, 2x + y = 48 is a linear equation with unknowns x and y. The value of x may be stated as follows:

2x + y = 48
2x = 48 – y
x = (48 – y) ÷ 2
Likewise, the value of y may be stated as follows:
2x + y = 48
y = 48 – 2x

Thus, for each x, there is a corresponding y to form pairs of solutions.

x =	0	1	-1	2	-2	3	-3	…
y =	48	46	50	44	52	42	54	…

When these pairs of solutions are plotted on a chart, they form a straight line as follows:

The equation of a line is y = mx+b, where x and y are coordinate points, m is the slope of the line, and b is the distance above or below x = 0 where the line crosses the y-axis. The line defined by y = -2x + 48 has a slope of -2, and it crosses the y-axis at x = 0 and y = 48.

Simultaneous Linear Equations

When two or more linear equations are satisfied by the same set of values, the equations are called simultaneous linear equations.

Example:

An investor invests $40,000 in three different properties that yield $1,494 in profit in the first year. The distribution of the profits was 3(½)%, 3(¾)%, and 4%. One-fourth of the investment amount was invested in the property that yielded the least amount of profit. We want to determine how much was invested in the other two properties.

Let x = the amount invested in property x at 3(½)%
Let y = the amount invested in property y at 3(¾)%
Let z = the amount invested in property z at 4%

Since the total investment was distributed among the three properties, the relationship between the individual properties and the investment amount is defined as:

x + y + z = $40,000

¼ of the investment amount was invested in property x, so

x = ¼ * $40,000
= $10,000

and the relationship is redefined as:

$10,000 + y + z = $40,000
y + z = $30,000

Since the total profit was acquired from all three properties, the relationship between the properties and profit is defined as:

3(½)%x + 3(¾)%y + 4%z = $1,494

Using the table of equivalents, we know that

½% = 50% and
3(½)% = 3.5%
also,
¾% = 75% and
3(¾)% = 3.75%

The relationship is redefined as:

.035x + .0375y + .04z = $1,494
(.035 * $10,000) + .0375y + .04z = $1,494
350 + .0375y + .04z = $1,494
.0375y + .04z = $1,144

We now have two simultaneous linear equations with two unknowns:

y + z = $30,000
.0375y + .04z = $1,144

To solve such equations, we must eliminate one of the unknowns and find the value of the remaining unknown. Once the value of this unknown is found, it is substituted in either of the original equations to find the value of the other unknown.

If the numerical coefficients of one unknown are the same and have like signs, subtracting one equation from the other eliminates the unknown in those equations. If the numerical coefficients are the same but have different signs, adding the two equations eliminates the unknown. If the numerical coefficients are not the same, decide which unknown is to be eliminated. Multiply the first equation by the coefficient of the unknown to be eliminated in the second equation, and multiply the second equation by the coefficient of the unknown to be eliminated in the first equation.

y + z = $30,000
.0375y + .04z = $1,144

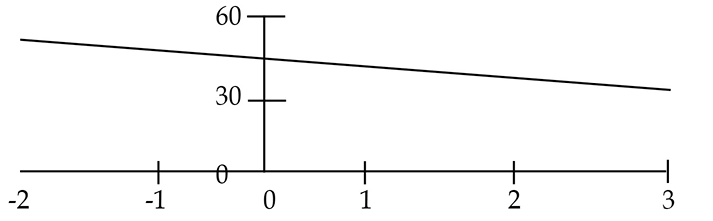
The coefficients of the unknowns are not the same. A decision is made to eliminate z using the coefficient 0.4 in the second equation to cancel z in the first equation.

0.4 * (y + z = $30,000)
0.4y + 0.4z = $30,000

We now have two equations with the same numerical coefficients of the unknown and like signs. The equations are subtracted to eliminate z:

Substituting the value of y in the first equation, we solve for z:

y + z = $30,000
$22,400 + z = $30,000
z = $30,000 – $22,400
z = $7,600

The investor invested $22,400 in property y at 3(3/4)% and $7,600 in property z at 4%.

An alternative method of finding a solution involves solving for one unknown in terms of the other unknown in one of the equations and then substituting the calculated value for the same unknown in the other equation. This creates an equation in one unknown, which can be solved. When one of the equations is solved, the result is substituted in the other equation to solve for the second unknown. Using the previous example:

y + z = $30,000
.0375y + .04z = $1,494

Solve for y in the first equation:

y + z = $30,000
y = $30,000 – z

Substitute this value of x in the second equation:

.0375y + .04z = $1,144
.0375 * ($30,000 – z) + .04z = $1,144
$1,125 – .0375z + .04z = $1,144
$1,125 – .0025z = $1,144
.0025z = $19
z = $7,600

Substitute this value in the first equation:

y + z = $30,000
y + $7,600 = $30,000
y = $22,400

Linear Equations in More Than Two Unknowns

When a system of linear equations involves more than two unknowns, the process of solving for unknowns is the same. Whether there are three equations in three unknowns or four equations in four unknowns, the objective is to eliminate one of the unknowns in favor of the others and to continue this procedure until there are only two equations in two unknowns. The values for the other unknowns are then found by substituting the values in the original equations. Though this is a lengthy process, it is not complex.

Example:

Jack assumes the role of property manager and records show that, over the past three years, purchases of supplies were made from a specific wholesaler. The records show discounts applied to bulk purchases, but it does not show the discount applied to the individual items. Jack needs to itemize the cost of each item to access the discount applied to each item purchased.

Year	Number of Items Purchased			Discount
	Hinges	Keys	Locks
1	10,000	5,000	2,000	$8,400
2	8,000	6,000	3,000	$7,900
3	9,000	4,000	4,000	$6,500

(1) 10,000x + 5,000y + 2,000z = $8,400
(2 ) 8,000x + 6,000y + 3,000z = $7,900
(3) 9,000x + 4,000y + 4,000z = $6,500

Each of these equations could be reduced by dividing each term by 100 to eliminate two zeros from each term of each equation.

(1) 100x + 50y + 20z = $84
(2) 80x + 60y + 30z = $79
(3) 90x + 40y + 40z = $65

It is determined that z will be the first term to be eliminated. We did not have to choose z; we could just as well have chosen x or y to be eliminated first. To eliminate z, equation (1) will be multiplied by 2 and subtracted from equation (3). Multiplying equation (1) by 2 ensures that the coefficient of z in equation (1) is the same as the coefficient of z in equation (3). Since the signs of the terms involving z are the same, equation (1) is subtracted from equation (3).

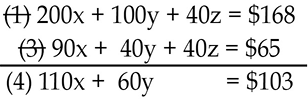
Now, to eliminate z in equation (2), equation (2) will be multiplied by 4, and equation (3) will be multiplied times 3 and then subtracted from equation (2).

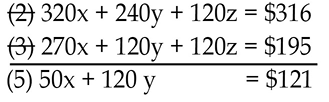
We have eliminated the unknown, z, and created two new equations in two unknowns, namely equations (4) and (5). We now need to eliminate one of the other unknowns. Using the equations that were generated in eliminating z, we have two equations in two unknowns, x and y. Once we solve for one of these unknowns, we can apply substitution to find the other unknown. We choose to eliminate the unknown y. Equation (4) will be multiplied by 2 and subtracted from equation (5):

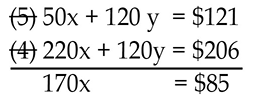
and x = $0.5 = 50 cents

We have now eliminated the unknown y, and we have a value for the unknown, x = $0.5. Substituting x in equation (4), we obtain the following value for y:

110x + 60y = $103
110($0.5) + 60y = $103
60y = $103 – $55
y = $48 ÷ 60
y = $0.8 = 80 cents

Substituting x and y in equation (1), we obtain the following value for z:

10,000x + 5,000y + 2,000z = $8,400
10,000($0.5) + 5,000($0.8) + 2,000z = $8,400
2,000z = $8,400 –$4,000 - $5,000
2,000z = –$$600
z = -$0.3 = -30 cents

The discount per item is:

X = 50 cents per hinge
Y = 80 cents per lock
Z = -30 cents per key

The wholesaler does not provide a discount on keys.

Quadratic Equations

A quadratic equation is an equation in which, in its simplest form, the highest power of any unknown term is in the form of a square (as in x2). Quadratic equations are also called equations of the second degree. The equation 4x2 + 9 = 3x2 – 15 is a quadratic equation, since the highest power of any unknown is a square. Since all unknowns of the equation are square, the equation is considered a pure or incomplete quadratic. The equation, x2 + x + 4 contains both a square and a power of the first degree. This equation is considered a complete quadratic.

An incomplete quadratic equation is solved for the unknown using the following steps:

• Simplify the equation to the form ax2 – b = 0.

• Isolate the unknown term (x2) to one side of the equation.

• Extract the square root of both sides of the equation.

The square root calculation results in roots as solutions that may be either positive or negative since the square root of x2 = ±x. Each of these roots must be substituted in the equation to determine which root actually satisfies the equation. As an example, the solution to 4x2 + 9 = 3x2 – 15 is calculated as follows:

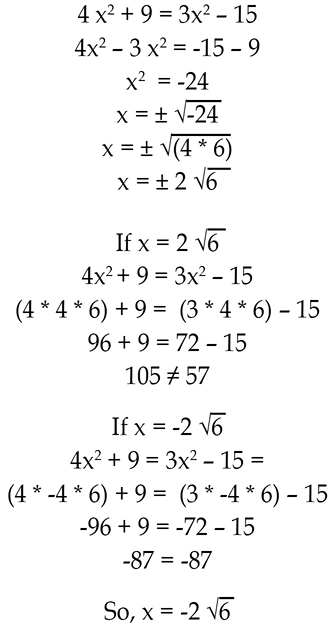
Complete quadratic equations may be solved by factoring. The process is as follows:

• Move all terms of the equation to the left hand side of the equation and set the equation equal to zero.

• Factor the left hand side of the equation.

• Let each term containing an unknown be set equal to zero.

• Solve each of the resulting equations.

As an example, the solution for the complete quadratic equation 4x2 – 2x = 3x2 + 8 is as follows:

4x2 – 2x = 3x2 + 8
4x2 – 2x – 3x2 – 8 = 0
x2 – 2x – 8 = 0
(x + 2) (x – 4) = 0

Let x + 2 = 0, then
x = -2
and substituting x = -2 in the original equation yields:
4(4) + 4 = 3(4) + 8
16 + 4 = 12 + 8
20 = 20

Let x – 4 = 0, then
x = 4
and substituting x = -4 in the original equation yields:
4(16) + 8 = 3(16) + 8
64 + 8 = 48 + 8
72 ≠ 56

So, x = -2 and x ≠ 4.

The Quadratic Formula

Any quadratic equation may be expressed by the quadratic formula ax2 + bx + c = 0, where a is the coefficient of the quadratic term, b is the coefficient of the linear term, and c is not unknown.

The solution to any quadratic equation is solved using the following quadratic formula:

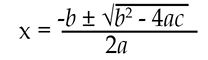
The equation x + 3 = 72 ÷ (x – 3) can be expressed as a quadratic equation as follows:

x + 3 =	72
	x - 3

(x + 3)(x – 3) = 72
x2 – 3x + 3x – 9 = 72
x2 – 81 = 0
The term involving x is equal to 0, such that b = 0.

The equation is solved as follows:

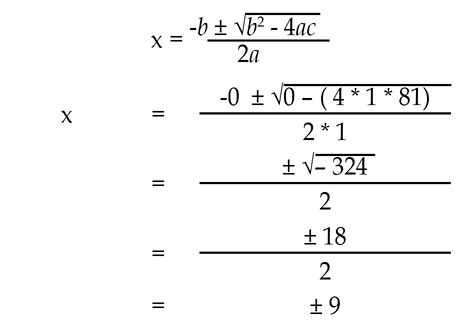
Measurements

Physical measurements have many applications in real estate and are essential in identifying properties and assessing the property value.

Measuring Surface and Space

Problems involving measurements are an integral part of real estate. Computations of acreage, footage, and other such measurements are necessary. Some of the most commonly used units of measure include inches, feet, and yards. Some of the less familiar units of measure may include chain, rod, and mile. Units used in measuring surfaces and space and their equivalents are as follows:

1 foot	= 12 inches
1 yard	= 3 feet
1 chain	= 66 feet
1 rod	= 16(1/2) feet
1 mile	= 5,280 feet

Linear Measures

The measurement of space may include linear measurements, area measurements, or volume measurements. Linear measurements measure the distance from one point to another. Linear measurements may be expressed using any of the units of measure indicated above.

3-D Linear Measures

An investment may involve property or some other commodity that occupies surface and space. The amount of surface or space that is occupied is usually identified by coordinates or by volume. Coordinates of a coordinate system are used to measure the length, width, and height of an object. Length is often assigned the value of x, width is often assigned the value of y, and height is often assigned the value of z. However, this assignment of coordinates is not absolute. Different individuals may define coordinates differently. The point is that an object must have at least two coordinate points to able to be defined on a surface and at least three coordinate points to be defined in space. Land is often measured by its width and length since its height is often defined as all space above and below the area defined by measured coordinates. In most land measurements, the z coordinate is equal to infinity. However, any structure placed on a parcel of land is likely to have some defined vertical measurement (or z coordinate).

Area Measures

Area measurement involves the measurement of surfaces. Some of the most commonly used units of area measurement and their equivalents include the following:

1 square foot	= 1 foot * 1 foot = 144 square inches
1 square yard	= 9 square feet = 3 feet * 3 feet
1 square mile	= 1 mile * 1 mile
1 acre	= 160 yards = 43,560 square feet
1 square mile	= 640 acres = 1 section
1 section	= 640 acres
1 township	= 36 sections

Areas are expressed in square feet. The formulae for determining area are as follows:

The area of any square or rectangle

= L * W

L = Length

W = Width

The area of any triangle

= ½ * B * Alt

B = Base
Alt = Altitude

The area of any circle

= � * R2

� = pi
R2 = radius squared

The area of any trapezoid

=	a + b	*	h
	2

a = length of one side
b = length of other side
h = height

Volume Measures

Volume measures are an extension of area measures. Volume measures add dimension and height (or depth) to area measurements. Some common units of volume measures and their equivalents are as follows:

1 cubic foot	= 1 foot * 1 foot * 1 foot = 1,728 cubic inches
1 cubic yard	= 27 cubic feet = 3 feet * 3 feet * 3 feet

The formulae for determining volume are as follows:

The area of any rectangle or cube	= Length * Width * Height	= L * W * H
The area of any triangular or cylindrical object	= Area * Height	= A * H
The area of any prism	= 1/2 (Base * Height * Width)	= 1/2 (B * H * W)

Directional Measures

Circles are the basis for directional measurements.

Circle	= 360 degrees
1 degree	= 60 minutes
1 minute	= 60 seconds
1 quadrant	= 90 degrees

Measuring Time

There are instances when periods of time will need to be measured. By expressing the beginning date and ending date of a time period in terms of year, month, and day, the elapsed period of time may be calculated. For example, the date of June 16, 1982 is expressed as 82-6-16. The date of March 25, 2006 is expressed as 06-3-25. The two dates should then be written with the earlier date placed beneath the later date as follows:

2006	3	25
1982	6	16

The earlier date is then subtracted from the later date. However, in our example, 6 months cannot be subtracted from 3 months. So, we take one from the year 2006 and add it to the months, such that the number of months is changed from 3 to 3 + 12 = 15, and the year changes from 2006 to 2005. The subtraction proceeds as follows:

The calculated time period is 23 years, 9 months, and 9 days.

Solving Problems

Problems in business and finance are not necessarily algebraic equations, but certain relationships are established from known facts. These relationships can then be stated as algebraic equations with the use of symbols, such as “x” or “a” to represent an unknown quantity. After a problem has been defined by equations, it is possible to readily solve the problem.

The ability to express algebraic relationships assists in developing an individual’s capacity for business reasoning and the understanding of business processes. While an individual that is not able to develop algebraic relationships may be quite capable of applying a specific formula, the individual that understands the wider implications of the procedures involved in the formula may be better capable to find a quicker solution or find a solution when the problem differs, however slight, from the problem for which a formula was designed to address.

Percentage Problems

The three basic arithmetic percentage problems discussed under “Arithmetic” may be easily expressed as equations when presented in certain form. Recall that the three basic percentage problems include finding the rate, percent of a number, and base. Using a substitution of mathematical terms for English terms, such problems may be expressed as algebraic equations. The substitutions are as follows:

• Convert the term “is” to the mathematical symbol “=”

• Convert the term “what” to the unknown variable “x”

• Convert the term “of” to the mathematical symbol “*”

• Convert the term “percent” to the mathematical symbol “%”

These substitutions are applied to problem statements to form mathematical equations as shown in Table 2.

Table 2: Converting Percentage Problems into Mathematical Equations
Basic Percentage Problems	English Problem Statement	Mathematical Equation
Finding the Rate	20 is what percent of 60?	20 = x% * 60
Finding the Percent of a Number	What is 20% of 60?	x = 20% * 60
Finding the Base	20 is 60% of what?	20 = 60% * x

Not all conversions from word problems to equations are so simple. Most conversions will require more thought. A clear understanding of the problem and the possible mathematical interpretations of the problem are necessary.

Percentage problems are of importance since the real world problems for which they are used are often confusing. The problem stems from determining the proper relationships between the base, rate, and the number under consideration. If any two of these values are known, the other value may be found once an appropriate problem statement is formed and substitutions are made.

Example 1:

We seek to find the percent of profit for an item that cost $100 and is then sold for $110. Some people are likely to indicate 10% since there is a profit of $10. However, profit and the percent of profit are two differing mathematical concepts. Profit is the amount made over and above the cost. Profit is expressed as a dollar amount. However, the percent of profit is that part of the cost that is profit. Percent of profit is expressed as a percentage. Recall that :

Is	implies	=
What	implies	x
Of	implies	*
Percent	implies	%

The problem statement is:

What percentage of the cost is the profit?

Substituting mathematical terms for English terms, the problem becomes:

x% * the cost = the profit
x% = the profit ÷ the cost
= $10 ÷ $100
= 0.1
= 10%
The profit is 10% of the cost.

Example 2:

If instead the problem involved determining what part of the selling price was the cost, the problem statement would be:

What percent of the selling price is the cost?

x% * the selling price = the cost
x% = the cost ÷ the selling price
= $100 ÷ $110
= 0.909
= 90.9%

The cost is 90.9% of the selling price.

Example 3:

If the problem involved determining what part the selling price was of the cost, the problem statement would be:

What percent of the cost is the selling price?

x% * the cost = the selling price
x% = the selling price ÷ the cost
= $110 ÷ $100
= 1.1
x = 110%

The selling price is 110% of the cost.

Clearly, one must first be able to properly define the relationship of the variables to develop a problem statement and then solve the mathematical statement. Making the same type of substitutions of English terms for mathematical terms the solutions to the previous three examples may be easily checked as follows:

The profit is 10% of the cost.

$10 = 10% * $100
$10 = .10 * $100
$10 = $10

The cost is 90.9% of the selling price.

$100 = 90.9% * $110
$100 = .909 * 110
$100 = $100

The selling price is 110% of the cost.

$110 = 110% * $100
$110 = 1.1 * 100
$110 = $110

The substitutions are applicable to any problem involving percentages. Other examples are as follows:

Example 4:

A home was listed for $175,000 and sold for 90% of the list price. We want to determine the sale price of the home.

The problem statement is:

90% of $175,000 is what?

.90 * 175,000 = x
x = $157,500

The sale price of the home is $157,500.

Example 5:

A firm’s top selling salesperson sold 132 of the 486 homes sold last year. We want to determine the percent of sales by the top selling salesperson. The problem statement is:

132 is what percent of 486?

132 = x% * 486
x% = 132 ÷ 486
x% = 0.271
x = 27.1%

Proportion Problems

Proportion is a measure of the equality of two ratios. A ratio is simply a fraction. A commonly used proportion is the reduction of a fraction to its lowest terms. As an example, the ratio, 25 ÷ 15 = 5 ÷ 3, is a proportion involving four terms: 25, 15, 5, and 3. A proportion always involves four terms. Using a substitution of mathematical terms for English terms, proportion problems may be expressed as algebraic equations. The substitutions are as follows:

• Convert the phrase “is to” to the mathematical symbol “÷”

• Convert the phrase “as” to the unknown variable “=”

These substitutions are applied to the problem statement to form mathematical equations as shown in Table 3.

Table 3: Converting Proportion Problems into Mathematical Equations
Basic Proportion Problem	English Problem Statement	Mathematical Equation
Find the proportion	a is to b as c is to d	a ÷ b = c ÷ d

The relationship among proportions provides for any one of the four terms to be determined if any three of the four terms is known. If it is known that the value 4 is to the value 13 as the value 200 is to some unknown value, then let the unknown term be assigned the value x. The value of x may be calculated as follows:

4	=	200
13		x
x	*	4	=	200
		13
x	=	200	*	13
				4
x	=	650

Example 1:

It took 9 men one day to dig 24 cubic yards of dirt to create the foundation for the basement of a house. A new house is being built that requires 80 cubic yards to be dug in two days. We need to determine how many men are necessary.

9 men are to 24 cubic yards as x men are to 80 cubic yards.

The proportion is solved as follows:

9	=	x
24		80
x	=	9	(80)
		24
x	=	30	men

This proportion is based on only one day. The dirt for the new house is to be dug in two days. As such, we assign the value x1 to the number of men required for 1 day and x2 be the number of men required for two days. We then divide x1 by 2.

x2 = x1 ÷ 2
x2 = 30 ÷ 2
x2 = 15 men

Example 2:

A lot is divided into three parts. 1/3 of the lot is used for building development, 1/8 of the lot is cultivated, and the remaining 125 acres is unused. We want to determine the total acreage of the lot.

The total acreage of the lot is 100% of the lot. Using the equivalences at Table 1, we determine that 1/3 of the lot is 33(1/3)% and 1/8 is 12(½)% of the lot. The remaining percentage is:

100% – 33(1/3)% – 12(1/2)%
100% – 33.3% – 12.5%
= 54.2%

Since 125 acres is 54.2% of the lot, we need to determine the acreage of the remaining 45.8% of the lot.

The proportion is:

125 acres is to 54.2% as x acres is to 45.8%

125	=	x
54.2%		45.8%
x	=	125	(.458)
		.542

x = 105.6 acres

The total acreage of the lot is:

105.6 acres + 125 acres
= 230.6 acres

Continued Proportion

Proportions are not always expressed as a ratio. If a proportional relationship involves more than two numbers, the method of distribution must be stated in the form of a continued proportion, such as 2:4:8. A continued proportion allows an amount to be distributed in a series of proportions. The 2:4:8 notation indicates that 2 parts are to be distributed to one member, 4 parts are to be distributed to another member, and 8 parts are to be distributed to a final member. The method for distributing an amount in proportion to a given series of numbers is as follows:

• Find the sum of the numbers in the series.

• Divide the amount by this sum.

• Multiply each number in the series by the resulting quotient.

Example 1:

Three partners decide to distribute profits according to the proportion 5:3:4. The profit of $14,400 is to be distributed to partner X in 5 parts, to partner Y in 3 parts, and to partner Z in 4 parts. The profit must be divided into 12 parts since 5 + 3 + 4 = 12.

$14,400 ÷ 12 = $1,200
Partner X’s share = 5 * $1,200 = $6,000
Partner Y’s share = 3 * $1,200 = $3,600
Partner Z’s share = 4 * $1,200 = $4,800

Elementary Statistics

Statistics provide a method of describing findings, making estimations, and making decisions. Statistics is the collection, classification, presentation, and interpretation of numerical data. All statistics are based on a population, which is a collection or set of individuals, objects, or measurements. Any subset of the population is known as a sample. Characteristics of a population are known as parameters and numerical characteristics of a sample are called statistics.

Average

There are many situations where the average (or mean) of some quantity will be sought. The arithmetic average of a series of values is calculated by adding all the values together and then dividing the sum by the total number of values. If the number of values in the series is represented as n and x1 represents the first value in the series, x2 represents the second value in the series,… and xn represents the last value of the series, then the average is calculated as:

avg = ( x1 + x2 + x3 … + x3 ) ÷ n

The sum of all the data points is denoted as ∑x. The average is denoted as follows:

avg = ∑x ÷ n

Example:

The average of the five values 98, 76, 45, 78, and 48 is calculated as follows:

98 + 76 + 45 + 78 + 48 = 345
345 ÷ 5
= 69

Measures of Dispersion

In statistics, several different measures are used to specify the spread or dispersion of data. The range, average deviation, variance, and standard deviation provide differing measures of dispersion that assist in describing a population of data.

Range

The range of data is a measure of the dispersion that measures the difference between the largest value and the smallest value in a set of data. These large and small values are also called the high and low values. Using the preceding example, the range is calculated as follows:

Range = H – L
= 98 – 45
= 53

The range indicates that the five values fall with 53 units, if measured on a number line.

Average Deviation

The average deviation is a measure of the dispersion of data about the average value. The dispersion of data about the average value is simply a measure of how far data points are from the average value, as measured on a number line. An individual data point is assigned the value x. The value of x deviates from the average value by an amount equal to xD = x – avg. The deviation is 0 if the data point happens to be equal to the average value. The data point is positive if it is greater than the average value and negative if it is less than the average value. Using the same data sample, the deviation (xD) of each individual data point is calculated by subtracting the average value from the value of the data point.

xD = x – avg, for all x

x	avg	xD
98	- 69 =	29
76	- 69 =	7
45	- 69 =	-24
78	- 69 =	9
48	- 69 =	-21
∑ ( x –avg) =		0

The sum of all deviations should equal zero. However, the sum of the absolute values of all the individual deviations provides an average deviation from the average value as follows:

| x – avg |, for all x

|29| = 29
|7| = 7
|-24| = 24
|9| = 9
|-21| = 21
∑ |x-avg| = 90

The average deviation from the average value is:

(∑ | x – avg | ) ÷ n
= 90 ÷ 5
= 18

Variance

The average deviation is rarely used, but it indicates the average distance that each data point is located from the average value. The more widely used measure of dispersion is variance. The variance provides a measure of the spread of all the data about the average value. The variance (s2) is calculated as:

s2	=	∑ (x – avg)2
		n –1

x - avg	(x - avg)2
29	841
7	49
-24	576
9	81
-21	441
∑ (x - avg)2 =	1988

s2 = ∑ (x – avg)2 ÷ ( n –1)
= 1,988 ÷ 4
= 497

The variance may also be expressed as follows:

s2 =	n∑x2 - (∑x)2
	n (n-1)

x	x2
98	9604
76	5776
45	2025
78	6084
48	2304
∑x = 345	∑x2 = 25793

=	5(25793) - (345)2
	5(5 - 1)
=	128965 - 119025
	20
=	9940
	20
=	497

The variance is a statistic that is used to compare one set of data with another. The larger the variance, the more dispersed the data.

Standard Deviation

Another widely used measure of dispersion is the standard deviation. The standard deviation is the positive square root of the variance, calculated as follows:

s = √( s2)
= √497
= 22.29

The standard deviation is also used to compare sets of data with one another. It also forms the basis for two important statistical principles: Chebyshev’s theorem and the empirical rule. Chebyshev’s theorem dictates that the proportion of any distribution of data, which lies within k standard deviations of the mean, is at least 1 – (1÷ k2), where k is any positive number greater than 1. From our example with k = 22.29, this theorem provides that:

1 – (1 ÷ k2)
= 1 – [1 ÷ (22.29)2]
= 1 – (1 ÷ 497)
= 1 –.002012
= 0.997988

At least 99.8% of the data falls within 22.29 standard deviations of the mean.

When data from a population is plotted on a histogram bar chart and the data is bunched around the mean and dispersed in both directions, the data is said to have an approximately normal distribution. The data points become more dispersed the further they are away from the mean. The empirical rule dictates that, if a variable is normally distributed, approximately 68% of the data will fall within one standard deviation of the mean; approximately 95% of the data will fall within two standard deviations of the mean, and about 99.7% of the data will fall within three standard deviations of the mean.

Probability

Probability is the relative frequency with which an event can be expected to occur. The probability that an event will occur may be measured empirically, theoretically, or subjectively. The empirical measure is based on experimentation or an observed relative frequency. Theoretical measures are based on the likelihood that one event is just as likely to occur as another. Subjective measures are based on intelligence and prior knowledge.

Empirical Measures

The probability P(A) of an event A occurring in n trials is determined using the formula:

P(A) =	nA
	n

where nA is the number of times that event A actually occurred.

Example 1:

In tossing a coin, the number of times for which heads will turn up and the number of times for which tails will turn up may be observed. In an experiment, a single coin is tossed and heads turned up in 104 out of 200 tosses. The observed empirical probability for the occurrence of heads is:

P(heads) = number of heads ÷ number of trials
= 104 ÷ 200
= 0.52
= 52%

Example 2:

A jar contains a red (R), yellow (Y), and green (G) marble. Two marbles are drawn from the jar and the probability of drawing a red marble is defined as P(R). The possible outcomes are called a sample space. The sample space includes six possibilities as follows:

RY	RG
YR	YG
GR	GY

P(R) = number of times that R was drawn ÷ sample size
= 4 ÷ 6
= 2/3

If the jar contains a mixture of red (R), yellow (Y), and green (G) marbles and two marbles are drawn from the jar, the probability of drawing a red marble is based on nine possible outcomes as follows:

RR	RY	RG
YY	YR	YG
GG	GR	GY

P(R)
= 5/9

In the preceding example, it is assumed that the jar had more than three marbles to choose from and that one colored marble was just as likely to be selected as the other.

Theoretical Measures

If the jar in the preceding example contained exactly 20 red marbles, 10 yellow marbles, and 15 green marbles, one particular colored marble is not as likely to be drawn from the jar as another. Since there are more red marbles than yellow or green, a red marble is more likely to be drawn. Likewise, since there are less yellow marbles than red or green, a yellow marble is less likely to be drawn. The theoretical probability of drawing the different colored marbles is calculated as:

P(any one color) = number of marbles of a particular color ÷ total number of marbles
P(R) = 20/45
P(Y) =10/45
P(G) = 15/45

Subjective Measures

Subjective measures are used to measure probability when equally likely events do not occur and no experiment has been or can be performed. The precipitation given in a weather forecast, for example, is a subjective probability where events are not equally likely to occur and no experiment can be performed to assign probability. Subjective probability is assigned based on personal judgment. The accuracy of such subjective probability is dependent upon one’s ability to correctly evaluate a situation.

In subjective probability, such personal judgment is expressed as a likelihood where the probability is assigned a numerical value between zero and one, with zero indicating that an event cannot or will not occur and one indicating that the event occurs every time. Further, the probability of all possible outcomes is equal to one.

0 ≤ P(A) ≤ 1
∑ P(A) = 1 for all outcomes

Example:

A weather forecaster indicates from personal judgment that it is eight times more likely to snow as to not snow. The sample space includes the probability of events: snow P(s) and no snow P(ns). The probability of all likely outcomes must be equal to one. So,

P(s) + P(ns) = 1

The subjective probability as defined by the forecaster is:

P(s) = 8 * P (ns)
Since P(s) + P(ns) = 1, we substitute for P(s), such that:
P(s) + P(ns) = 1
8 * P(ns) + P(ns) = 1
9 P(ns) = 1
P(ns) = 1/9

Substituting the value of P (ns) in the original equation, we find the P(s):

P(s) = 8 * P(ns)
= 8 * 1/9
= 8/9

The total sample space P(s) + P(ns) = 1 and (1/9) + (8/9) = 9/9 = 1.

Compound Probabilities

Compound probability combines several events. They include complementary events, mutually exclusive events, independent events, and dependent events.

Complementary Events

The complement of the event A is the set of samples in a sample space that do not belong to event A. The complement of event A is denoted as A’ and the probability of event A’ is denoted as P(A)’. For any given event, the following holds true:

P(A)’ + P(A) = 1
and
P(A)’ = 1 – P(A)

Example:

The probability of a selling a home in a newly established development within the next month is determined to be 76%. The probability of a sale is represented as P(A) = 0.76. As such, the probability of not selling is represented as P(A)’ and is calculated as follows:

P(A)’ = 1 – P(A)
= 1 – 0.76
= 0.24

Mutually Exclusive Events

Mutually exclusive events are events where one event precludes the occurrence of other events. In short, if one event occurs, others cannot occur. For example, if the event is the pulling of a ball from a hat, only one ball is selected. It cannot be both red and some other color at the same time. The probability of selecting a red ball and the probability of selecting a green ball are mutually exclusive events.

The compound probability of event A or event B occurring is represented as P(A or B), where A and B are mutually exclusive events. The probability is determined as:

P(A or B) = P(A) + P(B)
and
P( A or B or …or G) = P(A) + P(B) + … + P(G)

Independent and Dependent Events

Independent events are events where the occurrence, or non-occurrence, of one event does not affect the probability of the other. The compound probability that events A and B will occur is represented as P(A + B), where A and B are independent events.

P(A and B) = P(A) * P(B)
and
P(A and B and …and G) = P(A) * P(B) * … * P(G)

The lack of independence is dependence. The relationship between mutually exclusive, independent, and independent events is summarized as follows:

• If two events are mutually exclusive, they are also
dependent events.

• If two events are independent, they are not mutually exclusive.

• If two events are not mutually exclusive, they may be either dependent or independent.

• If two events are dependent, they may be either mutually exclusive or not mutually exclusive.

Conditional Probability

The compound probability that A will occur given that event B has occurred is represented as P(A|B) if A and B are independent events.

P(A|B) = P(A)
and
P(A|B) = P(A and B) ÷ P(B)

If A and B are dependent events, then

P(A and B) = P(A) * P(B|A)
or
P(A and B) = P(B) * P(A|B)

If A and B are not mutually exclusive, then

P(A or B) = P(A) + P(B) – P(A and B)

Example:

An investor wants to purchase hazard insurance for his personal residence and his rental property. Historical data suggests that the probability of filing a claim is 4/10 for the rental property and 5/100 for his personal residence. The probability of claims, given that these are independent events, is as follows:

The probability of a claim at both properties is:

= P(A and B)
= P(A) * P(B)
= 0.4 * 0.05
= 0.02

The probability of a claim at neither property is:

= P(A and B)’
= P(A)’and P(B)’
= 0.6 * 0.95
= 0.57

The probability of a claim at one of the properties:

P(A or B)
= P(A) + P(B)
= 0.4 + 0.05
= 0.405

Symbolic Logic

Logic is a branch of mathematics that is often overlooked. Logic is concerned with developing one’s ability to reason, and reasoning is fundamental to problem solving. Logic is concerned with arguments, which result from inference. Arguments of logic are not to be confused with fighting arguments. An argument in logic is any group of propositions, one of which is claimed to follow from the others, and the others are regarded as providing support or grounds for the truth of the other. Arguments are expressed as statements, and logic presumes that every statement is either true or false. As such, every statement has a truth-value that is either true or false. Further, there are two types of statements: simple and compound. A simple statement is a statement that does not include any other statement. A compound statement is a statement that contains other statements. “The wagon is red,” is a simple statement. “The wagon is red and the wagon rolls,” is a compound statement.

Symbolic logic provides methods of representing statements of argument with symbols and then determining the truth-value of such statements. Simple statements are either true or false, based on one’s perception or interpretation. As such, “The wagon is red” is true if the color of the wagon is red. However, the statement is false if the color of the wagon is blue.

Compound statements can be more complex and require the techniques of symbolic logic to symbolize statements. There are four primary types of compound statements. They include conjunctions, negations, disjunctions, and conditional statements. In symbolizing statements, one cannot merely rely on the placement of words in a statement. One must be capable of interpreting what the statement means and then restate that meaning in symbolic terms.

Arguments

“While poverty exists, the world is not perfect” is a compound statement that may be interpreted to mean, “If the world were perfect, there would be no poverty.” Assuming the original statement is true, the following statements are also true:

Either the world is perfect or poverty exists.

Unless poverty does not exit, the world cannot be perfect.

Several statements may be combined to form a valid argument, or a valid conclusion may be drawn from several given statements. The statements are called premises (or hypotheses) and a statement of result is called the conclusion. The process of going from premise to conclusion is called deduction. Sometimes the deduction of an argument is simple and other times it is not. A direct argument makes for the simplest type of deduction.

Example:

Hypothesis: All single-family homes are real property.

Hypothesis: All real property is real estate.

Conclusion: Then all single-family homes are real estate.

This may be easily demonstrated in a diagram.

Deduction is proof, but sometimes such proof is not available and indirect proof must be sought. Using indirect proof of a statement insists that all except a particular one must be false.

Conjunction

A conjunction is a compound statement that contains at least two statements, called conjuncts, and the word, “and.” A conjunction with statements, p and q, joined by the word “and” is true if and only if both of its conjuncts are true.

If p is true and q is true	then p and q are true
If p is true and q is false	then p and q are false
If p is false and q is true	then p and q are false
If p is false and q is false	then p and q are false

These statements form the basis for what is called a truth table. A truth table provides a method of representing the truth-values: true and false. The symbol used to represent the term “and” is *. The truth table for a conjunction is as follows:

p	q	p * q
T	T	T
T	F	F
F	T	F
F	F	F

Example:

We are given the statements:

The investor has an income property.

The investor has two properties.

We want to symbolize the argument, “The investor has two income producing properties.”

The argument must first be restated to form a compound statement. We only know that one property is income producing. We know nothing about the other property except that it exists. We restate and symbolize the argument as follows:

Let p = the investor has two properties = T

Let q = both properties are income producing = F

Therefore, the investor has two properties and both properties are income producing.

From the truth table, we see that:

p * q
= T * F
= F

Negation

A negation is a statement with the word “not” in it. The negation of a statement may be expressed by prefixing the statement with the phrases, “It is not” or “It is not the case that.” The negation of statement p is represented as ~p. The truth table for negation is as follows:

P	~p
T	F
F	T

Example:

Given the statement p = The investor has an income producing property.
We symbolize the statement: The investor does not have an income producing property, as:
~p

Disjunction

A disjunction, also called an alternation, is a compound statement with statements joined by the term the ”or.” A disjunction is true if at least one conjunct is true. The symbol used to represent the term “or” is v. The truth table for disjunction is as follows:

p	q	p v q
T	T	T
T	F	T
F	T	T
F	F	F

Example:

We are given the statements:

The investor owns an apartment building.

The investor owns a single-family home.

We symbolize the argument: The investor owns neither an apartment building nor a single-family home.

Let p = the investor owns an apartment building = T

Let q = the investor owns a single-family home = T

Therefore, the investor does not own an apartment building nor a single-family home. From the truth table, we see that:

= ~(T v T)
= ~T
=F

Deductive Reasoning

If A and B represent statements that are true and X and Y represent statements that are false, symbolic logic is used to deduce whether the relationships between the statements are true or false. The following examples make use of truth tables to determine whether the relationship between A, B, and C or A, B, X, and Y are true.

Example:

[ A v ( B v C) ] * [ ( A v B) v C]
= [ T or (T or T) ] and [ (T or T) or T]
= (T or T) and (T or T)
= T and T
= T

~ (A v Y ) * (B v X)
= not (A or Y ) and (B or X)
= not (T or F ) and (T or F)
= not (T and T)
= not T
=F

Conditional Statements

Conditional statements are compound statements of the form:

If antecedent then consequent

In a conditional statement, an antecedent (or implican) is expressed between the terms “if” and “then” and the consequent (or implicate) follows the term “then.” A conditional statement asserts that the antecedent implies the consequent. It does not assert that the antecedent is true. However, if the antecedent is true, it follows that the consequent is also true. Likewise, a conditional statement does not assert that the consequent is true. However, the consequent is true if the antecedent is true.

The symbolism used for conditional statements is כ, the horseshoe. The conditional statement “if p then q” is represented as p כ q. The truth table for conditional statements is as follows:

Example:

Argument: If the number 2 is less than the number 6, then any number less than 2 is less than 6.

Argument restated: If any number is less than 2, then that number is also less than 6.

Symbolism: If (x < 2) then (x < 6)

This equation is true for any value of x as follows:

	Statement	Truth Value
x = 1	If (1 < 2) then (1 < 6)	T כ T = T
x = 2	If (2 < 2) then (2 < 6)	F כ T = T
x = 3	If (3 < 2) then (3 < 6)	F כ T = T
x = -1	If (-1 < 2) then (-1 < 6)	T כ T = T

Inference

Inference involves testing an argument of form for proof of validity or invalidity. The statement p * g is a statement of form because, when statements are substituted for the variables p and q, a statement is formed. This discussion assumes that simple statements are neither logically false nor logically true. When one agrees with the premise of an argument and disagrees with the conclusion, for example, the argument is judged as invalid. Invalidity is proved by the method of logical analogy. If an argument is judged to be invalid, it does not mean there is no formal proof of validity, but a failure to discover formal proof of validity.

This book will not delve into further detail regarding the mathematics of logic, reasoning, and inference. We emphasize, however, that individuals involved in real estate need to have a certain level of reading comprehension to be able to interpret real estate contracts and property listings in order to formulate relevant problem statements and then find solutions to them. Some problems will require numeric computations to find solutions; other problems will require logic and reasoning, while others will involve both disciplines.

Example:

A partial property listing reads as follows:

The house is two-story, of brick construction, located in a residential subdivision of similar homes, built by the same builder at about the same time. There are four large bedrooms on the second floor, plus two bathrooms. There are hardwood floors throughout the first floor except the kitchen, which has a vinyl covering. The entire second floor, including stairs and baths, is carpeted. Owners have added a large below ground swimming pool, plus a bath house containing a sauna, and have had the grounds professionally landscaped at a cost of several thousand dollars. There is an automatic washer and electric dryer in the utility area.

Example 1:

We want to determine if all the bedrooms contain more than 90 square feet.

Let:

p = All rooms of the property are more than 90 square feet.

q = There are 4 large bedrooms.

Therefore, there are 4 large bedrooms, and the rooms are more than 90 feet.

The first premise is true because it may be concluded that 90 square feet represents a small room since 90 ft2 represents a room that is about 9 x 10 ft in size, which is a small room by any standard. The second premise is true since it is taken directly from the listing.

So, p = T, q = T and we determine p*q from the truth tables:

p * q
= T and T
= T

Example 2:

Let p = improvements total several thousand dollars

Let q = thousands of dollars is an over-improvement

Therefore, the property is over-improved.

p = T, q = F
from the truth tables:
p *q
T * F
= F

The argument is invalid since there is no information presented to indicate that thousands of dollars is an over-improvement. The invalidity of the argument does not mean the property is not over-improved, but that there is a failure to prove that it is.

Example 4:

Let p = appliances are included in the list price.

Let q = there is an automatic washer and dryer in the utility room.

Therefore, a washer and dryer are included in the list price.

p = F, q = T
from the truth tables:
p *q
F * T
= F

There is no information to suggest that the washer and dryer are included in the list price, even though the washer and dryer are appliances on the premises, and appliances located on the premises are often included in the list price. There is no information presented to indicate that it is or is not the case that the appliances are included in the price.

Table of Contents