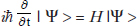Chapter VII

CONSTRUCTION OF THE ATOM IN THE TWENTIETH CENTURY

Yet the full account of the revolutionary developments in the twentieth century still has not been related, such as the inquiries leading to a more precise conception of the interior structure of the atom. In England one of the first attempts was the “plum pudding” model of J. J. Thomson that consisted of a positively charged mushy sphere on which the negatively charged electrons were embedded, like plums in a pudding, so that their exterior negative charges balanced the positive charge of the mushy interior producing a neutrally charged atom. Among the obvious faults of this model was his attributing the mass of the atom not to the interior substance, but to the exterior electrons, which would prove to be the reverse of the actual structure.

Rutherford, who began his research under Thomson and later would succeed him as Director of the Cavendish Laboratory, having left Cambridge for Montreal, now accepted a position in Manchester, England, were he conducted his own more sophisticated experiments to investigate the interior of the atom. Working in an excellent laboratory and aided by two talented assistants—Hans Geiger, who would invent the Geiger counter for measuring radiation, and Ernest Marsden, who had emigrated from New Zealand to study with his famous compatriot—Rutherford, decided to use his discovered α particles with their positive charge, large mass, and great velocity to probe the interior of the atom.

Instructing his assistants to radiate α particles at thin gold foil and measure the percentage of deflections striking a scintillating screen set at various angles, they found that most of the particles passed directly through the thin foil with a few deflected at slight angles by the presumed existence of the interior atoms. He then suggested that Marsden alter the angle of the screen to see if any of the α particles would be deflected at a greater angle and was astonished when Marsden reported that a few had actually been deflected straight backward to the eyepiece, as if they had been repelled by some massive component within the interior of the gold foil. As an indication of his astonishment, Rutherford described his reaction as “quite the most incredible event that has ever happened to me in my life. It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you.”⁷⁹

Undeterred by his astonishment, he began experiments to find a more precise explanation of the cause. Based on the measurements of the percentages of deflections at various angles, he devised a formula for measuring the angles of deflection, the velocity of the particles, and their charges. He also conceived of the nucleus as consisting of particles of a certain mass, along with a positive charge calculated by his formula indicating the atomic number of the element. Accordingly, he defined two of the properties of the nucleus, the atomic mass and the atomic number, that were independently confirmed by J. J. Thomson and H. G. J. Moseley based on X-ray emissions from the atom.

Apparently, from these X-ray emissions it was inferred that the atomic nucleus was surrounded by the negatively charged electrons, which are relatively massless, about 9 × 10^-28 g, or 1,836 times less than that of the proton, but whose shells occupy most of the volume of the atom confirming an earlier conjecture by Jean-Baptiste Perrin in 1901 that the structure of the atom might resemble the solar system:

Each atom might consist . . . of one or more positive suns . . . and small negative planets. . . . If the atom is quite heavy, the corpuscle farthest from the centre . . . will be poorly held by the electrical attraction . . . . The slightest cause will detach it; the formation of cathode rays [electrons] will become so easy that [such] matter will appear spontaneously “radioactive. . . .”⁸⁰

Indicative of how much progress was being made in explaining the structure of the atom Segrè states that the

new science of X-ray spectroscopy not only allows the study of deep electron shells and elementary chemical analysis on an unprecedented level of sensitivity and certainty: it also opens the way to the exploration of crystalline lattices and, more generally the architecture of solids and of molecules.⁸¹

It was decided that electrons in the outer shell cause the visible spectra, while the electrons in the inward shell are the source of the X-ray spectra. Apparently, it was Moseley’s and Thomson’s induced X-ray spectra that provided the evidence for the electron shells and Moseley who determined that the electron shells are related to the nuclear charge, thus providing independent evidence of the atomic number.

Becoming convinced that the experimental evidence supported his calculations, Rutherford presented his results first to the Manchester Literary and Philosophical Society in March 1911—the same society to which Dalton had submitted his atomic theory—and then sent a more detailed account in May to the Philosophical Magazine followed by another article entitled “The Structure of the Atom” in February 1914. Though he was unable to explain the exact causes of either atomic stability or radioactive instability, his conception of the composition of the nucleus and structure of the electron orbits was sufficient to enable physicists to formulate a clearer notational designation of the nuclear components and properties of the atom. For example, depicting the charge as plus or minus e and the number of the charged units as Z, then +Ze stood for the total charge of the nucleus with –Ze representing the total charge of the number of electrons in a particular atom.

Thus if there is an equal number of +Zes and –Zes, the charge of the atom is neutral, while ionization consists of the loss or gain of electrons and radioactive transmutations as a change in the nuclear number due to the emission of α, β, or γ rays. As Ne’eman and Kirsh state:

While emitting an alpha particle, the nucleus loses electric charge of +2e and a mass of about 4 amu. The process, which is also called alpha decay, or disintegration, lowers the atomic number Z by 2, and the mass number A by 4. The equation representing the alpha decay of uranium 238, for example, is: ₉₂U²³⁸ → ₉₀ Th²³⁴ + ₂He⁴.⁸²

Since the number of –Ze represents the number of electrons in the atom, which accounts for the chemical properties, it also indicates its place in Mendeleev’s Periodic Table. Since in neutral atoms the number of +Zes equals the number of –Zes, isotopes are atoms with identical chemical properties but different atomic weights. Yet while the chemical properties were attributed to the electrons, it still was not known what accounted for the nuclear numbers and weights. In 1919 Rutherford had discovered that when an a particle interacts with a hydrogen atom a hydrogen nuclear particle is ejected, but did this mean that atomic nuclei were all hydrogen nuclei?

After a number of experiments probing the nuclei of other atoms produced the ejection of the same entity, physicists decided they had discovered the first nuclear particle, naming it “proton,” after the Greek word protos meaning “first.” But they were still puzzled by the fact that the number of the nuclear particles of an atom did not match its mass or atomic weight. However, when James Chadwich, at the Cavendish Laboratory, probed the nuclei of lighter elements, such as beryllium, he discovered that a new particle was ejected that was quite massive but neutral in charge. Determining the mass of the particle to be nearly that of the proton and finding that it had a neutral charge, for obvious reasons he named it a “neutron” and received the Nobel Prize in 1935 for his discovery. Thus the discovery of subatomic particles was resolving many problems at a stroke, as Ne’eman and Kirsh affirm.

The discovery of the neutron is a classical example of the way in which the addition of a new building block clarifies as if by magic many previously inexplicable facts. For example, it became clear that the mass number A is just the total number of protons and neutrons in the nucleus. The fact that the atomic mass is always quite close to an integral number of amu found simple explanation: the masses of both the proton and the neutron are close to 1 amu. Different isotopes of an element are atoms the nuclei of which have the same number of protons but not the same number of neutrons. (p. 18)

Following his success in detecting the proton, deciding to eject α particles into the air Rutherford succeeded in producing nuclear disintegration. In an article titled “Collision of Alpha Particles with Light Atoms,” published in the June 1919 issue of the Philosophical Magazine, he describes in the fourth part “An Anomalous Effect in Nitrogen” in which the

nitrogen atom is disintegrated under the intense forces developed in a close collision with a swift alpha particle, and that the hydrogen atom which is liberated formed a constituent part of the nitrogen nucleus. . . . The results . . . suggest that if α particles—or similar projectiles—of still greater energy were available for experiment, we might expect to break down the nucleus structure of many of the lighter atoms.⁸³

Yet the model was mainly due to the great Danish physicist from Copenhagen, Niels Bohr (1885–1962), whom most physicists consider, along with Einstein and Rutherford, one of the three greatest physicists of the new era. Along with Einstein, he was a dominant influence on the development of theoretical physics in the first half of the twentieth century due to his own contributions and those of his famous Institute of Theoretical Physics in Copenhagen at which all the famous physicists of the era, such as Hendrik “Hans” Kramer, Wolfgang Pauli, Werner Heisenberg, Erwin Schrödinger, and Paul Dirac, etc., at one time attended.

The Cavendish Laboratory under the direction of Thomson being the most outstanding research center in physics, Bohr decided to do his postgraduate study there under the supervision of Thomson. However, having studied Thomson’s model of the atom carefully and found some faults in it, during their very first meeting after his arrival in the fall of 1911, he had the temerity to point them out to the famed physicist. Apparently not being accustomed to being corrected by a twenty-six-year-old graduate student who barely spoke English, Thomson did not appreciate the criticisms so the relationship, though not hostile, was not friendly.

Fortunately, however, in November Bohr met Rutherford in Manchester and then heard him lecture in Cambridge on his developing theory of the atom. These encounters led to his amicable departure from the Cavendish to study in Rutherford’s laboratory in Manchester where his association with Rutherford flourished to the extend that he considered him a kind of surrogate for his father who had died earlier. They remained close friends and admirers until Rutherford’s death in 1937.

Arriving in Manchester in March 1912, Bohr took courses in radioactivity and then, at the suggestion of Rutherford, began his own experiments investigating the nucleus with α particles. Realizing, however, that these nuclear experiments were not conducive to his primary theoretical interest in locating the electrons in the atom he decided to forego them. At the suggestion of two other research associates, Gorge von Hevesy, who was to become famous for his ingenious research in radioactivity, and Charles Darwin, the grandson of the famous evolutionist, who was experimenting on the effects of α particles on electrons, Bohr also began to investigate the impact of α particles on clusters of electrons to determine their placement within the atom.

In the summer of 1912 he prepared a draft article “On the Constitution of Atoms and Molecules,” known as the “Rutherford Memorandum” (which he showed to Rutherford), containing his criticisms of Thomson’s conception of the atom. First among the criticisms was the static placement of the electrons in the plum pudding model that Bohr thought untenable, yet, according to classical electrodynamics, if they revolved around the nucleus they would continue to radiate energy and eventually spiral into the nucleus, which also was unacceptable. Second, they could not rotate in the same shell because on classical principles that, too, would prove unstable. Third, on Thomson’s model the atom’s radius was not determined by the rotating electrons, but by the mushy positive interior, another apparent misconception.

Concluding that it would be “hopeless” to try resolving these problems in terms of classical mechanics, Bohr decided to incorporate Planck and Einstein’s quantification of radiation in his calculations. Like others at the time, initially he conceived the electrons as “atomic vibrators” that radiated according to Planck’s quantum of action as Bohr wrote in one of his famous articles published in 1913:

According to Planck’s theory of radiation . . . the smallest quantity of energy which can be radiated out from an atomic vibrator is equal to vk, where v is the number of vibrations per second and k (we now called it h) is Planck’s constant. Thus did the quantum theory enter the interior of the atom for the first time.⁸⁴

But the difficulty was acquiring the empirical data that would contribute to solving the problem. During the short time Bohr was at the Cavendish Laboratory he probably met John Nicholson, a gifted young researcher who in 1911 “associated spectral lines with various modes of vibration of electrons around their equilibrium orbits in the field of a central charge.”⁸⁵ In another article he proposed that the angular momentum of a revolving electron could be calculated from the mass, velocity, and the radius of its orbit. As Pais states: “If, therefore, the constant h of Planck has . . . an atomic significance, it may mean that the angular momentum of an atom can only rise or fall by discrete amounts when electrons leave or return” (p. 199).

But it was a suggestion of a student friend that led Bohr to consider the possible effect of electron orbits (rather than atomic oscillations) on the spectral emissions that produce the frequencies, especially in connection with Johann Balmer’s radiational formula introduced in 1885. The latter depicts the related mathematical frequencies of light emitted by hydrogen into a small number of series that provide the crucial insight. As Bohr recalled many years later: “As soon as I saw Balmer’s formula the whole thing was immediately clear to me. . . .”⁸⁶

What Bohr immediately realized was that Planck’s constant of action h at 6.62 × 10^-27 erg-seconds was the key to solving the problem of the orbits of electrons if he included it in his formula. Because h has a fixed value, by inserting it meant that the electron’s orbits could only take on specified values that were multiples of Planck’s constant. In addition, this indicated that any change from one orbit to another would require an exchange of energy: the absorption of energy if the electron jumped to a higher orbit or a discharge of energy if the electron dropped to a lower orbit. Furthermore, he inferred that since the exchange of energy came in a predetermined amount, it must be a form of electromagnetic radiation and also that E = hv meant the radiation involved definite frequencies since v stands for frequencies.

Thus Bohr’s solar model of the atom consisted of electrons surrounding the nucleus in a series of orbits called “stationary states” whose locations were dictated by Planck’s constant but whose orbital trajectories were determined by their angular momentum and energy or frequency. The emissions originated from a spaceless “jump” of the atomic electrons from one orbital or energy level to another. This also showed that not all transmutations originate in the nucleus as previously believed.

But there remained the original problem of why, according to classical physics, the electron at the lowest orbital state was not drawn into the nucleus by the electrostatic force eventually overcoming the energy of its angular momentum. This was solved by Bohr simply declaring that the “ground state is stable,” which Pais describes as “one of the most audacious postulates ever seen in physics.”⁸⁷

Bohr’s explanation was also “audacious” because it incorporated classical and quantum mechanics in an unorthodox way: he described the energy or frequencies of the particles’ angular momentum in terms of classical mechanics, while the optical frequencies of the ejected photons were described wholly in terms of quantum mechanics. This use of two conflicting mechanistic explanations, although related to different kinds of frequencies, is the first evidence of the two principles that would guide Bohr’s interpretation of quantum mechanics: the “correspondence principle” and the “principle of complementarity.”

Where the magnitudes of the frequencies of the electrons in the successive orbits resemble classical magnitudes the calculations tend to “correspond,” but where the magnitude of the optical frequencies of the ejected photons is much greater they tend to be “complimentary.” While unorthodox, the solution is similar in physics where relatively slow velocities are computed in terms of Newtonian mechanics and the greater optical velocities are computed by Einstein’s relativity theory.

Despite his model being largely theoretical, the derivations Bohr was able to infer from them were amazing, such as Balmer’s formula, Rydberg’s constant, deducing the radius of the bound state of the stable hydrogen atom (called the “Bohr’s radius”), and especially demonstrating that a series of stellar spectral lines that had been attributed to hydrogen were in fact the spectral lines of ionized helium.

In addition to these computational achievements, he was able to devise a number of new theoretical explanations of spectral emissions using such theories as blackbody radiation, the photoelectric effect, nuclear radioactivity, electron radiation, and spectroscopy. Also, by dividing the electron orbits into outer and inner shells he could attribute visible spectra to the outer electron shells while X-rays he explained were due to an electron being ejected from an inner shell. Beta rays, later identified as electrons, he correctly attributed to radioactive decay in the nucleus.

Although the above is just a cursory summary it does convey something of the magnitude of his accomplishments. Similar to Einstein’s five publications in 1905, at the early age of twenty-five, that revolutionized Newtonian mechanics, Bohr’s three publications in 1913 when he was twenty-eight years old on the orbital structure and function of electrons revolutionized atomic physics. Pais summarizes Bohr’s accomplishments:

The very existence of line (and band) spectra suggests, he noted, that electrons move in discrete stationary orbits inside atoms and molecules. Spectra (including X-ray spectra) arise because of quantum jumps between these states. . . . The quantitative confirmation of these ideas by his treatment of hydrogen and ionized helium mark a turning point in the physics of the twentieth century and the high point in Bohr’s creative career. The insistence on the role of the outermost ring of electrons as the seat of most chemical properties of the elements, in particular their valencies, constitutes the first step toward quantum chemistry. The sharp distinction between atomic/molecular and nuclear physics begins with his realization that β-rays emanate from the nucleus.⁸⁸

The response to these innovations, called the “Copenhagen interpretation,” were diverse with Rutherford, Arnold Sommerfeld, and Moseley favorable, while Otto Stern and Max von Laue declared, after reading Bohr’s 1913 article that, “if by chance it should prove correct, they would quit physics” (though they later changed their minds). It was Einstein who paid the most eloquent tribute becoming a close friend and admirer of Bohr despite his strong aversion later to quantum mechanics.

That this insecure and contradictory foundation was sufficient to enable a man of Bohr’s unique instinct and tact to discover the major laws of the spectral lines and the electron shells of the atoms together with their significance for chemistry appeared to me like a miracle—and appears to me as a miracle even today. This is the highest form of musicality in the sphere of thought.⁸⁹

But Bohr, aware of its ad hoc nature was somewhat uncertain of his theory of the hydrogen spectra, yet because of the general agreement of his solar model of the atom with the experimental evidence and consistency with other quantitative derivations, he accepted it as a provisional theory despite knowing that, due to the uncertain nature of the measurements, it lacked a definitive internal structure and firm independent reality. Still, as Pais indicates, his achievements were exceptional.

As the year 1913 began, almost unanimous consensus had been reached, after much struggle, that atoms are real. Even before that year it had become evident that atoms have substructure, but no one yet knew by what rules their parts moved. During that year, Bohr, fully conscious that these motions could not possibly be described in terms of classical physics, but that it nevertheless was essential to establish a link between classical and quantum physics, gave the first firm and lasing direction toward an understanding of atomic structure and atomic dynamics. In that sense he may be considered the father of the atom.⁹⁰

Although at the time Bohr’s solar model of the atom was mainly conjectural, its authenticity was reinforced by the supporting discoveries it engendered, to which we now turn. Among the things he could not explain was the reason that electrons in the hydrogen atom were restricted to their particular orbits and why their angular momentum was an integral multiple of Planck’s constant h, or depict the atomic spectra of atoms with an electronic structure more complex than hydrogen. This awaited the discoveries of the “new quantum theory,” in contrast to Bohr’s “older quantum theory,” begun in 1923 as a result of the successive contributions mainly of A. H. Compton, Louis de Broglie, Werner Heisenberg, Paul Dirac, and Erwin Schrödinger, along with Wolfgang Pauli, Pascual Jordan, and Max Born.

One of the first to begin the transition was Prince Louis de Broglie who, assisting his older brother Duke Maurice in his experiments on the dual properties of light, presented in 1923 his doctoral dissertation to the French Academy of Sciences on “The Connection between Waves and Particles.” Recall that to explain blackbody radiation Planck had introduced in 1900 the concept of the “quantum of energy” to designate the discontinuous or discrete exchange of energy caused by the light waves striking the oscillating electrons within the metal to produce the ejected electrons, but he had restricted it solely to the interaction occurring within the metal. In contrast, in 1905 Einstein explained the photoelectric effect as not due to light waves striking the metallic surface but to a stream of light particles colliding with the electrons within the metal, which light particles were later named “photons.”

Having no mass, in order to eject the electrons from within the metal the light particles had to possess a certain quantity of energy that Einstein defined as hf (Planck’s constant h times the light frequency f) per particle. So, though light produced diffraction patterns characteristic of waves when injected through a tiny aperture, it also displayed the properties of particles when reflected on metals causing an interaction with the inner vibrating electrons. This duality of contrary properties introduced one of the two main paradoxes of quantum mechanics, the other being the uncertainty of the measured properties.

The duality was further evidenced when in 1922 the American physicist Arthur Compton discovered that when paraffin was irradiated with X-rays a portion of the emerging waves had longer wavelengths than the entering ones. Compton believed the effect was not explainable by the usual wave theory of electromagnetic radiation but could be explained if light consisted of quanta of energy some of which was transmitted to the electrons in the paraffin due to the collisions. So even if the light quanta do not have mass, they do have momentum owing to the energy.

His experiment showed that “a photon of electromagnetic radiation of wavelength λ carries momentum whose value is p = h/λ, where h is Planck’s constant, λ the wave length, and p the momentum. Compton explained that in the collision with an electron the photon loses momentum, and therefore its wavelength increases by the scattering.”⁹¹ Thus the explanation of blackbody radiation, the photoelectric effect, and Compton’s experiment reinforced the validity of the dualism of light despite the paradoxical contradiction of properties.

Intrigued by light having particle properties, de Broglie decided to investigate as his dissertation subject whether the converse was true, that particles could have wave properties. Ne’eman and Kirsh summarize his revolutionary theory as follows.

Every moving particle has an associated wave of definite wavelength and frequency determined by the mass and velocity of the particle. The laws of motion of small particles cannot be understood unless the wave nature of the particles is taken into account, just as the photoelectric effect and black body radiation cannot be understood without resort to the particle properties of light.

The mathematics of this model was simple. De Broglie assumed that the equations E = hf and p = h/λ were valid for material particles as for photons. Thus, the wavelength, λ, of the particle is given by λ = h/p where p is its momentum. The faster the particle moves, the shorter is its wavelength. (pp. 39–40)

De Broglie’s dualistic theory contributed to Bohr’s orbital model of the atom by explaining that if electrons possessed wave properties, the circumference of the orbital circle would have to be an integral number of wavelengths, otherwise they would interfere and destroy. He also calculated the angular momentum of the circular orbits of the electrons that could be observed in a cloud chamber. Yet other questions pertaining to Bohr’s model were still unexplained: why the electrons in the hydrogen atom were restricted to their particular orbits? what accounts for their orbital jumps? and what were the atomic spectra of atoms that had an electronic composition more complex than hydrogen?

Furthermore, there was the paradox that while the path of an electron is determined by Newton’s mechanistic laws its stability within the atom required the laws of quantum theory. Since the latter laws did not conform with Newtonian laws a new set of laws and theoretical framework had to be formulated, named “quantum mechanics,” to describe this new system of subatomic particles. The initially proposed explanations were the “matrix mechanics” of Werner Heisenberg (1901–1976) and the contrasting “wave mechanics” of Erwin Schrödinger (1887–1961).

If one would like to know of a readable account of the turmoil facing young physicists in the early twentieth century owing to Bohr’s introduction of the solar model of the atom, the dualism between the wave and the particle properties of electrons, and the necessity of using both Newtonian and quantum laws, I know of no more fascinating book than Heisenberg’s biographical account, Physics and Beyond: Encounters and Conversations (1971), recounting his intellectual development and outstanding contributions to the current revolutionary developments in physics quoted earlier.

Owing to his decisions to study atomic physics, enroll at the University of Munich, and attend the lectures of Arnold Sommerfeld from 1920 to 1922, he was privileged to have been invited by Sommerfeld to hear the lectures by Bohr, then age thirty-seven, in the summer of 1922 at what has come to be known as the “Göttingen Bohr Festival” at Göttingen’s famous school of mathematics. Having been introduced to Bohr by Sommerfeld and then, during the question period following a lecture titled “Advanced Objections,” to Hendrik “Hans” Kramer’s speculations on quantum mechanics discussed by Bohr during the lecture, Bohr was so impressed by Heisenberg’s comments that at the end of the discussion period he asked Heisenberg to join him on a walk that afternoon over the Hain Mountain. As Heisenberg wrote: “This walk was to have profound repercussions on my scientific career, or perhaps it is more correct to say that my real scientific career only began that afternoon.”⁹²

During their walk Bohr began the conversation by indicating what initially had been his main concern in physics, saying that it was not what one might think, the inner structure of atoms, but the “stability of nature,” an insight also as to how a great scientist thinks. Giving examples to show that classical Newtonian science took for granted the normal stability and uniformity of nature in formulating the laws and mathematical equations that describe the causal connections and inner structure of the Newtonian ­corpuscular-mechanistic worldview, Bohr’s basic motivation was not merely to describe their stability and uniformity but to explain what accounts for it.

As quoted by Heisenberg, Bohr stated:

My starting point was not at all the idea that an atom is a small-scale planetary system and as such governed by the laws of astronomy. I never took things as literally as that. My starting point was rather the stability of matter, a pure miracle when considered from the standpoint of classical physics. (p. 39)

He then explained what he meant by the stability, persistence, and recurrence of the physical and chemical properties of the elements in terms of their combining in definite proportions to constitute the molecular structures of certain substances while retaining their original properties when decomposed, which forms the basis of the classifications in Mendeleev’s Periodic Table. Still, the connection between the stability in nature and Bohr’s fascination with atomic structure is revealed in a statement he made, again quoted by Heisenberg:

The existence of uniform substances, of solid bodies, depends on the stability of atoms; that is . . . quite inexplicable in terms of the basic principle of Newtonian physics, according to which all effects have precisely determined causes, and according to which the present state of a phenomenon or process is fully determined by the one that immediately preceded it. This fact used to disturb me a great deal when I first began to look into atomic physics. (p. 39)

This also reveals the radical distinction between the scientific orientation of Bohr and Einstein, despite their close friendship and enduring admiration for each other, the latter searching for a formula that would describe a four-dimensional space-time field that would precisely unify all the laws and structure of the universe while the former was trying to determine the nature of the subatomic structures that produce the underlying probabilistic causal interactions in nature. Accordingly, Bohr describes all the developments in the past few decades that led to the realization of the limitations of classical physics and the need to replace or supplement it by an understanding, however tenuous, of the deeper subatomic realm (pp. 39-40).

Bohr then presents his position that seems to have had a lasting effect on Heisenberg. This position affirms that since classical physics deals with our familiar macroscopic world it can provide visual or verbal representations of that world while subatomic or quantum physics investigates a domain that is so unique that it does not allow such ordinary descriptions. As Bohr clearly states in a quotation by Heisenberg:

We know from the stability of matter that Newtonian physics does not apply to the interior of the atom; at best it can occasionally offer us a guideline. It follows that there can be no descriptive account of the structure of the atom; all such accounts must necessarily be based on classical concepts which, as we saw, no longer apply. You see that anyone trying to develop such as theory is really trying the impossible. For we intend to say something about the structure of the atom but lack a language in which we can make ourselves understood. (p. 40)

In response to these skeptical reflections, Heisenberg bluntly asks Bohr what was the point of his introducing “all those atomic models” in his lectures and what did he expect to show by them, to which Bohr replies: “These models have been deduced, or if you prefer guessed, from experiments, not from theoretical calculations. I hope that they describe the structure of the atoms as well, but only as well, as is possible in the descriptive language of classical physics” (p. 41).

Heisenberg next asks how can we ever expect to understand the nature of atoms if a description of their inner structure is not clearly defined? Hesitating momentarily, Bohr replies, “I think we may yet be able to do so. But in the process we may have to learn what the word ‘understanding’ really means” (p. 41). His answer foretells the eventual “uncertainty” in the conception of the interior structure of the atom as well as those inherent in quantum mechanics in general.

Impressed by the conversation with Heisenberg, Bohr invited him to Copenhagen to attend Bohr’s Institute, but finding Bohr’s attempt to construct the inner structure of atoms on the experimental evidence unappealing, Heisenberg decided instead to go to Göttingen in the fall of 1924 to study with Max Born whose approach to atomic physics was based more on the mathematical calculations. Owing to his father being a professor of Greek at the University of Munich, Heisenberg had learned to read the Greek classics in the original when he was just sixteen years old. Thus, like Kepler, he became attracted to atomic physics by reading Plato’s Timaeus, which equated the four basic elements of fire, earth, air, and water, along with the cosmos, to the five Pythagorean geometric solids. Despite his realization that the endeavor seemed to be “wild speculation,” Heisenberg “was enthralled by the idea that the smallest particles of matter must reduce to some mathematical form (p. 8).

Suffering from a severe attack of hay fever in Munich the following summer, Heisenberg sought shelter in the small island of Heligoland on the North Sea where the sea breeze dispersed any pollen-laden air. It was there he began writing a paper on “electron states” based entirely on the measured light frequencies absorbed or emitted by the atom that was published in Zeitschrift für Physik (Writing on Physics) in September 1925. As he indicated, despite rejecting any attempt to visualize the interior structure of the atom, like Plato he seemed to find in the numbers a kind of abstract mathematical reflection of its interior.

Within a few days . . . it had become clear to me what precisely had to take the place of the Bohr-Sommerfeld quantum conditions in an atomic physics working with none but observable [or measurable] magnitudes. . . . The energy principle had held for all the terms, and I could no longer doubt the mathematical consistency and coherence of the kind of quantum mechanics to which my calculations pointed. At first, I was deeply alarmed. I had the feeling that, through the surface of atomic phenomena, I was looking at a strangely beautiful interior, and felt almost giddy at the thought that I now had to probe this wealth of mathematical structures nature had so generously spread out before me. (p. 61; brackets added)

The paper did contain peculiar mathematical functions when the matrices were added, subtracted, and especially when multiplied, unlike those of traditional mathematics, that he was unable to explain. But given the fact that such famous mathematicians as David Hilbert, Richard Courant, and Max Born were among his colleagues at Göttingen University, when shown to Born the latter recognized the incongruities, especially the violation of what is known as the commutative law. The law states that when multiplying two numbers the order of the numbers is irrelevant: 9 × 8 = 8 × 9, but Heisenberg did not find this to be true of his calculations.

When shown the paper Born was not perplexed because he recognized it as an example of matrix mechanics. As authors Crease and Mann state:

Born was one of the few physicists in Europe—perhaps the only one—with a good knowledge of matrix mathematics. He realized that Heisenberg’s quantum-theoretical series were nothing more, nothing less, than awkward manipulations of frequency matrices. . . . Born was delighted. Rewriting Heisenberg’s equations as matrices led to a whole new world of applications he could explore.⁹³

Yet it still required some interpretation as the continuing quotation indicates:

The first thing he figured out was that the matrix q for position and the matrix p for momentum are noncommutative in a very special way: that is, pq is not only different from qp, but the difference between pq and qp is always the same amount, no matter what p or q you chose. Mathematically he wrote this pq - qp = ħ/i, where ħ, as usual, is Planck’s constant divided by twice pi, and i is the special symbol mathematicians use for the square root of minus one. (p. 50)

But still not satisfied Born, with the aid of Pascual Jordan (who wrote most of the article because Born had suffered a nervous collapse), published a paper also in the Zeitschrift für Physik that described the basic mathematics of what later became known as matrix mechanics. As described by Ne’eman and Kirsh:

They arranged the measurable quantities in square arrays of numbers (such arrays are called “matrices”) and by defining mathematical operations between these matrices, they created a consistent quantum mechanical theory. This version of quantum mechanics, which has been known as matrix mechanics, succeeded in explaining certain experimental facts in atomic physics and even predicted unknown phenomena which were verified later experimentally.⁹⁴

For their contributions Heisenberg won the Nobel Prize in 1932, when he was only thirty-one years old; Dirac, together with Schrödinger, in 1933; and Born in 1954. Ne’eman and Kirsh add that the “number of important contributions” Heisenberg “made to physics exceeded that of any other physicist in the twentieth century, except Einstein” (p. 44). I would state, and Bohr.

As an indication of how intriguing the mathematics of quantum mechanics was in those early days, Paul Dirac, a close friend of Heisenberg with whom he had discussed atomic theory in their student days, and who collaborated with Born in writing several articles, also favored a mathematical construction of the interior of the atom rather than Bohr’s solar model. After receiving a copy of Heisenberg’s paper and studying it for little over a week, he “sat down and wrote an alternative formulation, which presented quantum mechanics as a coherent axiomatic theory” (p. 44).

In my discussion I may have quoted statements that gave the impression that Heisenberg remained very satisfied with his introduction of matrices in place of Bohr’s pictorial electron orbits, but later I read a statement by him quoted by Crease and Mann that apparently shows his misgivings in working with a purely numerical system such as matrices despite its earning him the Nobel Prize. It was written to Pauli after Heisenberg wrote his famous article in collaboration with Jordan and Born published in the Zeitschrift für Physik.

I’ve taken a lot of trouble to make the work physical, and I’m relatively content with it. But I’m still pretty unhappy with the theory as a whole and I was delighted that you were completely on my side about [the relative roles] of mathematics and physics. Here I’m in an environment that thinks and feels exactly the opposite way, and I don’t know whether I’m just too stupid to understand the mathematics. Göttingen is divided into two camps: one, which speaks, like [the prominent mathematician David Hilbert] (and [another mathematical physicist, Herman Weyl ], in a letter to Jordan), of the great success that will follow the development of matrix calculations in physics; the other, which, like [physicist James Franck], maintains that the matrices will never be understood. I’m always annoyed when I hear the theory going by the name of matrix physics. For awhile, I intended to strike the word “matrix” completely out of the paper and replace it with another [term] — “quantum-theoretical quantity,” for example.⁹⁵ (italics, brackets, and parentheses are in the original)

How different his present dissatisfaction with matrices is from his youthful intention of replacing physical objects with mathematical symbols.

But as might be expected, not all the physicists at the time were disdainful of visual model building, the Viennese-born Erwin Schrödinger (1887–1961) being an outstanding example. Attracted to de Broglie’s discovery that particles also have wave properties that are physical and observable, he was the physicist Einstein consulted when asked by the committee examining de Broglie’s doctoral dissertation of its credibility, but also being undecided Einstein did not give his approval until Schrödinger assured him that the thesis had merit.

Schrödinger, influenced by Einstein’s belief that fields should replace material particles as the fundamental reality along with de Broglie’s discovery that particles have wave properties, decided to see if a complete wave theory could be formulated to replace Bohr’s electronic solar model. De Broglie had shown that although mass and momentum were considered properties of particles, they also could be depicted as functions of waves. Such equivalences had previously been discovered: Einstein showing the equivalence of mass and energy (E = mc²) and Planck that energy could be equated with frequency (e = hv). Since waves have energy and energy has mass, it was possible that material particles could be depicted as waves as well as particles.

Starting with the classical wave equation that describes the spatial properties of electromagnetic waves, Schrödinger began investigating whether a wave equation could be found to describe the wave properties of subatomic particles, one that would supplement the equations of Newtonian mechanics. In four papers he presented his new theory of “wave mechanics” that appeared in Annalen der Physik (Annals of Physics) from January to April 1926 with the title “Quantization as an Eigenvalue Problem.”

Among his publications he proposed that waves should be considered the basic reality and introduced what is now known as the “celebrated” Schrödinger’s wave equation 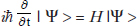that contains the famous scalar wave function Ψ(psi), along with the Hamiltonian H, “which is simply the observable corresponding to the energy of the system under consideration.”⁹⁶ As explained by Pais, in replacing particles with waves he

suggested that waves are the basic reality, particles are only derivative things. In support of this monistic view he considered a wave packet made up out of linear harmonic oscillator wavefunctions . . . a superposition of eigenfunctions so chosen that at a given time the packet looks like a blob localized in a more or less small region. . . . He examined what happened to his packet in the course of time and found: “Our wave packet holds permanently together, does not expand over an ever greater domain in the course of time.” This result led him to anticipate that a particle is nothing more nor less than a very confined packet of waves, and that, therefore, wave mechanics would turn out to be a branch of classical physics, a new branch, to be sure, yet as classical as the theory of vibrating strings or drums or balls.⁹⁷

According to the equation, between measurements the state vector known as the “wave function” moves in an undisturbed, regular way as described in classical physics until it is measured, which then causes it to collapse into an eigenvalue or single value that produces the observation. Thus its state is uncertain until measured. Owing to its being an extension of classical wave theory, formulated in a mathematics more familiar than matrix mechanics, and providing a visualizable explanation, it was acclaimed by most physicists. As described by Crease and Mann,

the mathematics Schrödinger used was much easier for physicists to understand. . . . If it was hard to imagine how a solid object like an atom could really be made out of waves—what was making the waves?—many physicists had confidence that Schrödinger, a clever fellow, would figure out the answer.⁹⁸

Moreover, as also explained by Crease and Mann, Schrödinger even proposed an explanation as to how particles could be considered as waves.

A particle was in reality nothing but “a group of waves of relatively small dimensions in every direction,” that is, a sort of tiny clump of waves, its behavior governed by wave interactions. Ordinarily, the bundle of waves was small enough that one could think of it as a dot, a point, a particle in the old sense. But in the microworld, Schrödinger argued, this approximation broke down. There it became useless to talk about particles. At very small distances, “we must proceed strictly according to the wave theory, that is, we must proceed from the wave equation, and not from the fundamental equation of mechanics, in order to include all possible processes.” (p. 56)

Unfortunately, these expectations turned out to be illusory. Instead of determinate or distinct portrayals of the electron states of the atom, the solutions to Schrödinger’s wave equation produced small cloudlike images reminding one of Rorschach ink blots. Yet even Born, who contributed to the article creating matrix mechanics, after reading Schrödinger’s first paper wrote that he was drawn to the traditional aspects of Schrödinger’s wave mechanics, a view that angered Heisenberg.

But then, surprisingly, on April 12, 1926, after a very careful perusal of both matrix mechanics and Schrödinger’s wave mechanics,

Pauli sent a lengthy letter to Jordan in which he proved that the two approaches were identical [or more accurately stated mathematically equivalent]. Schrödinger himself proved the same thing, a little less completely, a month later. . . . In the equivalence paper, Schrödinger mentions pro forma, that it was really impossible to decide between the two theories—and then went on to argue fiercely the merits of wave mechanics. (p. 57; brackets added)

Yet despite his attraction to the more traditional approach of Schrödinger’s wave mechanics compared to matrix mechanics, during his investigations Max Born made a discovery described in two papers titled (in translation), “Quantum Mechanics of Collision Phenomena,” published in the Zeitschrift für Physik in June and July of 1926 that challenged Schrödinger’s claim that wave mechanics, based on measurements of actual waves, was closer to classical physics than matrix mechanics, which dealt only with abstract numerical matrices. The June paper discovered an indeterminacy or uncertainty in Schrödinger’s method of determining the position of alleged particles by measuring the density of wave packets.

Calling it the “measurement problem,” Born found that the impact of the measurement would actually produce a “scattering” of the waves in the “wave packet” causing an indeterminacy in the measurement. Producing an unavoidable uncertainty or probability in the measurements in wave mechanics contrary to the strict causality and determinism in classical mechanics, he concluded that this showed it was not closer to traditional physics as Schrödinger claimed. According to Pais: “It is the first paper to contain the quantum mechanical probability concept.”⁹⁹ In his June paper Born described the scattering by a wave function Ψ_mn’ where the label n symbolizes the initial beam direction, while m denotes some particular direction of observation of the scattered particles. At that point Born introduced quantum mechanical probability: “Ψ_mn determines the probability for the scattering of the electron . . . into the direction [m].” (p. 286)

In the second paper, published in July, he interpreted Schrödinger’s wave function |Ψ|² as the probability for locating the “particle” at the point of greatest density in the wave packet, adding to the measuring probability the probability of quantum states. Although Born had originally believed that Schrödinger’s wave mechanics led back to a more traditional interpretation of subatomic physics, his probabilistic interpretations convinced him otherwise. As stated in his autobiography:

Schrödinger believed . . . that he had accomplished a return to classical thinking; he regarded the electron not as a particle but as a density distribution given by the square of his wave function |Ψ|^2.. He argued that the idea of particles and of quantum jumps be given up altogether; he never faltered in this conviction. . . . I, however, was witnessing the fertility of the particle concept every day in . . . brilliant experiments on atomic and molecular collisions and was convinced that particles could not simply be abolished. A way had to be found for reconciling particles and waves.¹⁰⁰

Just as Newton’s conception of absolute space and time that were based on measurements made by rods and clocks that were unaffected by the relatively slight velocities of the earth had to be revised when Einstein discovered that when approaching the velocity of light measuring rods contract, clocks slow down, and mass increases (to account for the invariant velocity of light), so measurements of the subatomic or quantum world, assuming that they would follow the same Newtonian calculation method, when actually measured, would have to be radically revised.

As usual, physicists were confounded when they encountered the wave-particle duality, the statistical nature of quantum mechanics, and the uncertainty principle due to the interacting measurements at the subatomic level of inquiry that refuted the Newtonian assumption of the universality of the laws of nature at all levels or scales of inquiry. Here again we encounter a further aspect of the third radical revision in our conceptions of reality at different dimensions or levels of inquiry. The bewilderment decreased somewhat when it was discovered that the formalisms of Dirac’s theory, Schrödinger’s wave mechanics, and Heisenberg’s matrix mechanics were equivalent: according to Emilio Segrè, “[f]or all three the essential relation that produces the quantification is pq – qp = h/2πi . . . [while] for Heisenberg p and q are matrices; for Schrödinger q is a number and p the differential operator p = h/2πi ∂/∂q . . . [and] for Dirac p and q are special numbers obeying a noncommutative algebra. . . .”¹⁰¹ But the dispute continued with Bohr inviting Schrödinger to his Institute in Copenhagen on October 27, 1926, to discuss their theoretical differences with such intensity that Schrödinger became ill from the tension during the exchange, even though Bohr had the reputation of being a “very considerate and friendly person by nature.” Yet no resolution was reached.

After Schrödinger left Copenhagen Bohr carried on his dispute with the same intensity with Heisenberg, who was an associate at his Institute at the time. Trying to resolve their differences with Bohr defending the view that the solution depended on forging the correct conceptual framework and Heisenberg insisting, as usual, that the resolution would depend upon devising the correct mathematical formalism, they, too, arrived at an impasse. Frustrated and exhausted by these intense discussions, Bohr decided to take a skiing trip to Norway to relax leaving Heisenberg at the Institute to pursue his investigation.

Concentrating on his measurement problem, as a result of his discussion with Bohr, Heisenberg decided to investigate the difficulty involved in measuring the position and momentum of a particle under a gamma ray microscope. The latter is used because its short wavelength provides great accuracy in determining the position, but according to Planck’s formula ε = hv, a short wavelength also has a high frequency with high energy such that the interaction between the wave and the particle adversely affects the precision of the momentum measurement. To reduce the inaccuracy of the latter a longer wavelength is required, but that produces less certainty in the position measurement.

Rather than trying to remove the discrepancy, by the end of February 1927, Heisenberg had decided to accept it as unavoidable and devise a formula to state what initially came to be known as the famous “uncertainty or indeterminacy relations.” An appreciation of the radical change involved is seen if contrasted with what was taken for granted in classical mechanics as stated by Pierre-Simon Laplace in 1886.

An intellect which at a given instant knew all the forces acting in nature, and the position of all things of which the world consists . . . would embrace in the same formula the motions of the greatest bodies in the universe and those of the slightest atoms; nothing would be uncertain for it, and the future, like the past would be present to its eyes.¹⁰²

It was this assurance that nature is governed by exact laws that would disclose a final knowledge of the universe at all dimensions that Heisenberg was rebutting. Having accepted the conjugate indeterminacy, Heisenberg sought a mathematical formula that would describe the resultant uncertainty. Although the conditions necessary for measuring the conjoined values of the conjugate magnitude’s position and momentum, along with energy and time, could not be precisely measured, either of the dimensions alone could be exactly determined, but the more precise the measurement of one the less precise the measurement of the other. As Heisenberg expressed this mathematically: if the uncertainty in accuracy of the measurement of each of the interdependent conjugate attributes is represented by the delta symbol (Δ), then the product of the conjoined magnitudes momentum p and position q cannot be reduced to less than Planck’s constant barred, Δp × Δq must be equal to or greater than ħ. The second uncertainty states that in the time interval Δt the energy can only be measured with an accuracy equal to or greater than ħ.

Heisenberg published the results in the April 1927 issue of the Zeitschrift für Physik. Having received the proofs of the article, Bohr sent a copy to Einstein “adding in an enclosed letter that it ‘represents a most significant . . . exceptionally brilliant . . . contribution to the discussion of the general problems of quantum theory.’”¹⁰³ What makes it exceptional is not just the calculated mathematical equation, as significant as that is, but that it reversed the age-old assumption that for the mathematics to be correct it must accurately represent the experimental results. Heisenberg affirmed that it is the mathematics that limits or sets the possible experimental outcome! As he states:

Instead of asking: How can one in the known mathematical scheme express a given experimental situation? the other question was put: Is it true, perhaps, that only such experimental situations can arise in nature as can be expressed in the mathematical formalism? The assumption that this was actually true led to limitations in the use of the concepts that had been the basis of classical physics since Newton.¹⁰⁴

As an indication of the influence Heisenberg’s paper had on Bohr, when a famous article by Einstein, Podolsky, and Rosen (known as the EPR article), titled “Can Quantum Mechanical Descriptions of Physical Reality Be Considered Complete?” was published in the Physical Review in 1935,¹⁰⁵ claiming that although Heisenberg’s formalism was consistent with all the known quantum data it was “incomplete” because it did not allow precise measurements of the conjugate attributes’ position and momentum and energy and time, Bohr had a ready reply.

In the following issue of the Review, in an article with exactly the same title, he replied that in quantum mechanics

we are not dealing with an incomplete description characterized by the arbitrary picking out of different elements of physical reality at the cost of sacrificing other elements, but . . . the impossibility, in the field of quantum theory, of accurately controlling the reaction of the object on the measuring instruments. . . . Indeed we have . . . not merely to do with an ignorance of the value of certain physical quantities, but with the impossibility of defining these quantities in an unambiguous way.¹⁰⁶

In the draft of a paper in July 10, 1927, Bohr had used the term ‘complementarity’ for the first time that became a famous designation for the conjugate uncertainty measurements. Then in a collection of articles published later in his life, there is a clear statement of how he believed quantum mechanics has changed our method and understanding of the subatomic quantum domain in contrast to the macroscopic and atomic level of experience, an explanation that had assumed that a precise description and definite explanation of the external world was always possible, even if out of reach at the time:

Within the scope of classical physics, all characteristic properties of a given object can in principle be ascertained by a single experimental arrangement. . . . In quantum physics, however, evidence about atomic objects obtained by different experimental arrangements exhibits a novel kind of complementary relationship. Indeed, it must be recognized that such evidence which appears contradictory when combined into a single picture is attempted, exhausts all conceivable knowledge about the object. Far from restricting our efforts to put questions to nature in the form of experiments, the notion of complementarity simply characterizes the answers we can receive by such inquiry, whenever the interaction between the measuring instruments and the objects forms an integral part of the phenomena.¹⁰⁷

Just as we found that our sensory system modifies what we observe, so we have learned that what unobservable properties the world discloses experimentally at a certain dimension also partially reflects the methods and instruments used in investigating it. This realization that all experience and knowledge is due to an inter­action with the world, not just an immediate awareness or disclosure of it as usually appears to be the case, brought about a radical transformation in our conception of reality and how we come to know it—a reversion especially imposed by Heisenberg’s discovery of the “uncertainty principle” and Bohr’s “Copenhagen interpretation” that has been a crucial feature of the third scientific transformation of our conception of reality.

What is surprising is that Einstein, in his article with Podolsky and Rosen, did not realize that the uncertainties encountered when investigating a deeper domain of particle physics did not permit the same exact measurements as those made on a larger scale was analogous to his special theory of relativity. His theory also claimed that the exact measurements of space, time, and motion made within the lesser velocities of ordinary experience cannot be made when the velocities are so extreme they effect the measuring devices such that the measurements are relative to the velocities of the measurer rather than being absolute as Newton claimed.

For millennia humans believed that the picturesque world as ordinarily experienced was the actual world. Even as late as the nineteenth century Ernst Mach declared that “Atoms cannot be perceived by the senses . . . they are things of thought” implying they did not exist. Yet at the beginning of modern classical science, with the introduction of the telescope and the microscope, scientists began to realize that the existence of the ordinary world, as objective, determinate, and independent as it appears to be, really depends on very complex, unseen underlying conditions. With every discovery of a new dimension of the world the assumption usually has been that this must be the final reality, not just another level of inquiry.

But even if all existence and knowledge is conditional, it is equally erroneous to infer that we do not know anything about the world or that it has any objective properties as concluded in the article by Einstein, Podolsky, and Rosen if the quantum mechanical worldview were accepted. But were their view true, how could we account for the corrective and progressive advances in scientific knowledge and its extraordinary technological consequences before and since their time?

Supposing that whatever knowledge of the universe and human existence we acquire depends upon the physical conditions within which they exist, along with the method of investigation used, this does not preclude their being actual within those conditions, otherwise we would have to deny that the ordinary world we live in exists and that the independent subatomic world does not have any of the physical properties it has because their existence is dependent on a more extensive background physical context. Consider water existing as vapor or ice under different conditions.

What we have to realize is that the meaning of ‘existence’ has changed with the acquisition of greater knowledge, just as Bohr argued that the meaning of ‘understanding’ has changed. Just because particles are so minute that they prevent the measuring of certain conjugate properties does not mean that these properties do not exist in the object conjointly—that the particle does not have a simultaneous position and momentum or energy and time just because the conditions prevent their being measured conjointly. How could it exist without these conjugate properties?

As added evidence of this conception of “contextual realism” that I referred to in a previous book bearing that title and again in this book, I’ll continue the review of additional scientific discoveries showing the limits, not necessarily the negation, of Newton’s corpuscular-mechanistic view of reality at a deeper level of inquiry, along with illustrating that additional physical or quantitative properties of subatomic particles have been discovered despite their existence being dependent upon the type of measurement used to identify them.

The first is the property of spin. It is common knowledge that microscopic particles are not defined by sensory qualities, but by their primary properties of mass, charge, energy, and momentum. At about the time the previously described quantum mechanical discoveries were being made, two physics students in their mid-twenties from the University of Leyden in Holland, Samuel S. Goudsmit and George E. Uhlenbeck, suggested that on Bohr’s model, electrons like planets, in addition to having an orbital motion around the nucleus, also revolve on their axes with an invariant angular momentum called “spin,” whose value is ½h/2π. This value remains constant “even when the electron is outside the atom, and is totally independent of the linear speed or environment of the electron,”¹⁰⁸ indicative of its inherent though conditional nature. Furthermore, because the electron is electrically charged and follows the laws of quantum mechanics, it has two additional properties.

First, having an electrical charge it acts as a tiny magnet whose movement creates a magnetic moment that creates an electromagnetic field. Second, in quantum mechanics an entity with the properties of angular momentum has just two possible spin orientations: “If we perform any measurement whatsoever to determine the angle between the direction of the electron spin and any given direction in space, we find that the angle is always either 0⁰ or 180⁰—in other words, the spin is either parallel or antiparallel to the chosen direction” (pp. 53, 55). Moreover, the spin of certain pairs of subatomic particles are such that measuring the spin of one particle will instantly cause its twin particle to begin spinning in the opposite direction at the same rate, however great the distance between them, a discovery made by John Stewart Bell and published in the Review of Modern Physics in 1966. Given these perplexing features of quantum mechanics, it has been claimed that the concept of spin as an actual rotary motion of the electron should not be taken literally: “it is more accurate to say that the electron has an intrinsic angular momentum of ½h/2/π, called spin, as if it were rotating about its axis” (p. 57). But how is it possible to use “as if states” in scientific theorizing?

For example, the concept of spin is considered an additional important property of electrons and other particles, having explanatory as well empirical consequences that have been experimentally confirmed. The electric charge along with its spin gives the electron its magnetic moment that helps explain the emission and reabsorption of photons. In addition, the two possible spin orientations imply two energy states that help explain “the peculiar pattern of close lines or doublets in the Balmer series of the hydrogen spectrum.” Called quantum electrodynamics or QED for short, the theory measured the magnetic moment of the electron “in a unit called the Bohr magneton, denoted µ_e” that has “a very great accuracy . . . found to be 1.001 159 652 µ_e” (p. 58).

As another example of the remarkable influence Bohr’s Institute had on the development of quantum mechanics, during the time that Schrödinger and Heisenberg were at the Institute, Paul Dirac also was present doing postdoctoral work from September 1926 to February 1927. Like Schrödinger, he hoped to reconcile quantum mechanics and relativity theory by incorporating Einstein’s concept of the field and reformulating Heisenberg’s quantum mechanics, along with incorporating the Hamiltonian, the operator corresponding to the total energy of a system. As described by Crease and Mann:

Using Heisenberg’s quantum mechanics, Dirac was able to come up with the Hamiltonian for the atom from quantum mechanics. Dirac was thus able to say that the Hamiltonian for the entire process could be found by adding up the separate Hamiltonians for the atom, the field, and the interaction. . . . The result was the first quantum field theory. Because it linked quantum theory with the dynamics of electromagnetic fields, Dirac called it quantum electrodynamics.¹⁰⁹

He submitted his results in an article to the Proceedings of the Royal Society toward the end of January 1927, just three weeks before Heisenberg conveyed his uncertainty principle to him. In succeeding papers he published his well-known relativistic wave equation, which has come to be known as the “Dirac equation” that Pais says “ranks among the highest achievements of twentieth-century science.”¹¹⁰ In 1928 he devised “a relativistically invariant equation for an electron” whose mathematics “introduced a new internal degree of freedom of the particle. This degree of freedom turns out to have all the properties of the electron spin, starting from its value h/4π. It also has a magnetic moment of value eh/ 4πmc.”¹¹¹

As proof of its validity, these properties of spin and magnetic moment were not introduced ad hoc but as properties predicted by the equations. Along with sharing the Nobel Prize with Schrödinger in 1933, in the previous year, as an acknowledgment of his outstanding achievements, Dirac was appointed to Newton’s chair of Lucasian Professor of Mathematics at Cambridge University that was occupied by the famous cosmologist Stephen Hawking until his recent retirement.

Yet like medicines that have wonderful curative powers but also unexpected side effects, Dirac’s equation produced very puzzling outcomes. For instance, his equation predicted that when the electromagnetic field was quantized and included Heisenberg’s uncertainty principle space was no longer empty, but filled with bizarre entities and occurrences, as described by Crease and Mann:

The spaces around and within atoms, previously thought to be empty, were now supposed to be filled with a boiling soup of ghostly particles. From the perspective of the quantum field theory, the vacuum contains random eddies in space-time: tidal whirlpools that occasionally hurl up bits of matter, only to suck them down again. Like the strange virtual images produced by lenses, these particles are present, but out of sight; they have been named virtual particles. Far from being an anomaly, virtual particles are a central feature of quantum field theory, as Dirac himself was soon to demonstrate.¹¹²

But as peculiar as these predictions were, there was another just as weird. When the Hamiltonian (energy) of a single electron was predicted from his equation it showed two possible values, one negative and one positive. The existence of positive energy was of course well-known, but no one had ever encountered negative energy. Also, when using his improved Wilson cloud chamber to detect cosmic waves Carl D. Anderson observed tracks of what appeared to be light particles. On further investigation to determine whether they were negatively or positively charged, he found they were positive. Thus he accidentally discovered a new particle with a mass comparable to an electron but with an opposite positive charge that he named ‘positron,’ after the electron. Given their opposite charges, when they interact they annihilate thereby producing two photons. Consequently, he had discovered a new kind of matter called “antimatter.” According to Crease and Mann:

From an embarrassment the negative energy states were transformed into a triumph for quantum electrodynamics, the first time in history that the existence of a new state of matter had been predicted on purely theoretical grounds. Dirac won the Nobel Prize in 1933; Anderson went to Sweden three years later. (p. 90)

In the following decades Dirac’s quantum electrodynamics (QED), consisting of six quarks, six leptons, and five bosons, was developed into what became known as “the standard model” independently identified by three physicists: the Japanese born Sinitiro Tomonaga and two Americans, Richard Feynman and Julian Schwinger, all three receiving the Nobel Prize for their achievement in 1965. (I believe it was on July 4 or the 5, 2012, that the scientists at the European Organization for Nuclear Research (CERN) in Geneva announced the discovery of the Higgs boson, or “God particle” as it is now called.) Applying quantum mechanics to electromagnetic fields and to electrons (with the wave function of the electron also considered a field), they treated the fields not as a continuum but composed of discrete quanta.

According to Chris Quigg at the Fermi National Accelerator Laboratory (Fermilab):

QED is the most successful of physical theories. Using calculations . . . developed in the 1940s by Richard P. Feynman and others, it has achieved predictions of enormous accuracy, such as the infinitesimal effect of the photons radiated and absorbed by the electron on the magnetic moment generated by the electron’s innate spin. Moreover, QED’s descriptions of the electromagnetic interaction have been verified over an extraordinary range of distances, varying from less than 10^-18 meter to more than 10⁸ meters.¹¹³

Continuing research on the magnetic moment, in 1933, after enhancing the original Stern-Gerlach experiment, Stern found that the magnetic moment of the proton was three orders smaller than that of the electron and that of the neutron, and despite being neutral has a “negative magnetic electric charge” similar to the proton. As typical of scientific inquiry, these “facts hinted that the neutron (and also the proton) have an internal structure which includes positive and negative charges, because magnetism always involves the motion of charges.”¹¹⁴

Additional contributions were made by Wolfgang Pauli that include the introduction of the “exclusion principle,” the hypothesis of the “neutrino,” and the importance of spin in determining which particles and in what number can occupy an atomic orbit. An Austrian physicist with an unusually critical and acerbic manner who occasionally signed his communications with “The Wrath of God,” Pauli nonetheless was a gifted scientist who gained the esteem of his colleagues. His major contribution, “the exclusion principle” introduced in February 1925, added to Bohr’s earlier explanation of the limitation of the kinds and numbers of electrons that could occupy the successive stationary orbits in his solar model of the atom. For this he was awarded the Nobel Prize in physics in 1945.

In due course it was found and proven theoretically that the Pauli exclusion principle is valid for any particle whose spin is not integral, i.e., [whose spin is] [1/2, 3/2, 5/2, etc. The laws of behavior of these particles are embodied in “Fermi-Dirac statistics.” . . . These are the statistics characterizing distinguishable objects. The particles themselves are called fermions. . . . Protons and neutrons are also fermions (spin ½) and thus in a nucleus they populate different energy levels just as the electrons in the atom do. (p. 60; brackets added)

In contrast, particles with integral spin or whole numbers are called “bosons” (after the Indian physicist S. N. Bose who, along with Einstein, identified them) and are not affected by Pauli’s exclusion principle. Not being distinguishable by the four quantum numbers, they are governed by another kind of statistics named the “Bose-Einstein statistics” and since they are capable of having the same quantum numbers an unlimited amount can be located in a particular region of space. “It can be shown that the difference between fermions and bosons is related to the connection between the spin and the symmetry of the wave function of the particles” (p. 60).

Along with the discovery of the spin vector and quantum numbers, physicists were attempting to determine the sizes of the various particles that the wave-particle duality with its contrasting properties, along with the uncertainty principle with its obscurity, made particularly difficult. In the thirties physicists tried to measure the diameter of the electron and “arrived at the formula r = e²/mc² where e and m are the charge and mass of the electron and c the speed of light. This gave a value of 3 × 10^-13 centimeters for the radius” (p. 61). But calculations made within the system QED, where the electron is considered a mere point, showed a more miniscule value of 10^-16 centimeters while experiments on protons and neutrons “show that their mass and charge concentrated in a region with a diameter of about 1.2 × 10^-13 centimeters (p. 61).

I shall now endeavor to present as lucidly and comprehensively as possible the subsequent discoveries of the major subatomic particles and forces that culminates the third revolutionary scientific development that not only extended or replaced Newtonian classical science, but also led to the creation of the contemporary conception, called “Quantum Chromodynamics,” of the inner composition of the subatomic particles previously mentioned. This proved exceedingly difficult because of the illusiveness and vagueness of the experimental evidence and the much greater reliance on mathematics. As a result the two major contributors to the new “Standard Theory,” Richard Feynman and Murray Gell-Mann, were at times in agreement and at times quite opposed, though it was Gell-Mann’s interpretation that usually prevailed. His contributions to particle physics were extraordinary: the property of strangeness,V-A, the Eightfold Way, quarks (although for a long time he wavered as to whether they were real or just artifacts to preserve the mathematical symmetry), quantum chromodynamics (QCD), along with many others discoveries too numerous to cite.

The succeeding decades of the twentieth century following the Second World War, owing to the creation of the atomic bomb and the increasingly powerful atomic accelerators, such as the Large Hadron Collider at CERN, near Geneva; the Fermi National Accelerator Laboratory (FNAL) in Batavia, Illinois; the Brookhaven National Laboratory; and the Stanford Linear Accelerator (SLAC) produced the detection of a deeper domain of subatomic particles and forces by accelerating and colliding a deeper level of particles. Created out of the mass-energy equivalence stated in Einstein’s formula E = mc², they were predicted and/or discovered by such outstanding scientists as Eugene Wigner, Richard Feynman, Murray Gell-Mann, Julian Schwinger, Steven Weinberg, Sheldon Glashow, Hideki Yukawa, Samuel Ting, Burton Richter, Harald Fritzsch, and many others.

Such a mélange of new particles have been discovered along with the previously mentioned basic particles, such as the proton and neutron, that they have been compared to a zoo and required the creation of a new periodic table composed of hadrons with the hadrons further divided into baryons and mesons. Two new forces were added to gravity and electromagnetism, a strong force binding the nucleons and a weak force explaining the radio­activity within the nucleus that only acts within short distances. Furthermore, previous forces acting at a distance were superseded by an exchange of “virtual particles,” photons in electromagnetism, gluons in strong interactions, and the vector bosons W^-, W⁺, and Z^o in weak interactions. While hadrons react to both strong and weak forces, leptons only respond to the weak force consisting of the exchange of three bosons and photons.¹¹⁵

As usual, at first it was thought that the hadrons and leptons, along with the photons and hypothesized gravitons completed the list of basic particles, but in 1964 Murray Gell-Mann and George Zweig introduced further particles accounting for the structure of the hadrons that Gell-Mann whimsically named “quarks” (taken from a passage in James Joyce’s Finnegans Wake, “Three quarks for Muster Mark!”), that caught on! They do not have integral charges but fractional charges of plus two-thirds or minus one-third. And like the ancient “minima” of Epicurus, they never exist separately but are conjoined as pairs or triplets to form hadrons, a quark and an anti-quark comprising mesons and three quarks forming a baryon. Although originally they were just conjectures to explain the interactions of the hadrons, their depicted combinations into hadrons have been verified.

Continuing the discoveries endowed with fanciful names, two new charges were postulated, one called “strangeness” by Gell-Mann and another referred to as “charm” by Glashow, enabling physicists to account for hadrons and their interactions based on combinations of quarks classified as “flavors”: up (u), down (d), charm (c), strange (s), bottom/beauty (b), and top/truth (t) (pp. 291–95). Thus matter was classified into two groups, one consisting of six leptons and another of six quarks. Then a new quantum theory analogous to quantum electrodynamics (QED), based on the Yang-Mills gauge theory and group theory, was conceived and named “quantum chromodynamics” (QCD for short) by Gell-Mann (p. 291). It was so named because it consisted of a strong force or charge called “color” that binds the quarks within the hadrons.

Further unifications occurred when Glashow combined the weak and electromagnetic forces into an “electroweak theory” and Stephen Weinberg introduced the concept of “symmetry breaking” by the (postulated) Higgs boson introduced to explain how Glashow’s W and Z particles acquired mass, the existence of which has been recently confirmed to the great satisfaction of nuclear physicists. The unification continued when in 1969 the Dutch physicist Gerardus ‘t Hooft discovered that Cartan’s group theory could be applied to gauge theories that allowed Weinberg in 1973, utilizing the color charge, to create “a gauge field theory of strong forces,” the basis of QCD (pp. 278–79).

But the weak forces were still unaccounted for. Thus Glashow and James Bjorken wrote a paper in which they suggested that a new quark called “charm” could link QCD with the electroweak theory, despite the difficulty of its confirmation because quarks do not exist independently, but only in self-enclosed couplets or triplets within the hadrons. Yet their existence was eventually confirmed. And so the discoveries continued with the detection by Samuel Ting at Brookhaven and Burton Richter at SLAC of a new particle called “J” by Ting and “psi” by Richter, now known as the “J/Y particle.” They were awarded the Nobel Prize in 1976 for their discovery, and Glashow, Weinberg, and Salem shared the prize in 1979 for contributing to the theory of electroweak and electromagnetic interactions between elementary particles. And as a kind of culmination, Carlo Rubbia and Simon Van der Meer were awarded the Nobel Prize in 1984 for their confirmation at CERN of the existence of the W^-, W⁺, and Z⁰ particles. Feynman, Schwinger, and Tomonaga had been awarded the Nobel Prize in 1963 while six years later in 1969 Gell-Mann was the single recipient of the prize for his numerous outstanding contributions to physics.

Despite these significant advances, the attempt to unify the strong and weak forces had just begun. Glashow and Howard Georgi advanced the effort toward unification in a series of papers published in 1973–1974, one of which carried the impressive title “Unity of All Elementary-Particle Forces.” If successful, their Grand Unified Theory (GUT as it came to be called) would combine quarks and leptons into one family, owing to their decaying into one another, while a “superweak force” was introduced to unify strong and electroweak interactions. Later in the same year Georgi, Weinberg, and Helen Quinn wrote a paper declaring that at very high temperatures or energies, such as existed at the time of the Big Bang, all the forces were unified. While not yet confirmed, at least the initial framework of a Grand Unified Theory was constructed.

In an Atlantic Monthly article published in 1984 with the bold title “How the Universe Works,” Crease and Mann summarized these achievements as follows:

The result is a ladder of theories. Firmly on the bottom is SU(3) [a Family of eight baryons Gell-Mann again fancifully designated the “eightfold way” after Buddha] × SU(2) × SU (1) [the SU stands for special unity group based on Cartan’s group theory], whose predictions have been confirmed (“to the point of boredom,” Georgi says). . . . The W and Z particles were discovered at CERN . . . but the theory was so well established by then the event was . . . anticlimactic.

The GUTS proposed by Georgi and Glashaw and other physicists, that fully unite the strong, weak, and electromagnetic forces, are the next rung on the ladder. Although as yet unconfirmed . . . these theories are considered compelling by most physicists. Finally, at the top of the ladder, in the theoretical stratosphere, are supersymmetry and its cousins, which are organized according to a principle somewhat different from SU(5), though, like that model, they put apparently different particles together in groups. Supersymmetry groups are large enough to include gravity, but are so speculative that many experimenters doubt they can ever be tested.¹¹⁶ (brackets added)

Although published many years ago and therefore somewhat dated, the quotation presents an excellent summary of developments up to that time showing how radically different the scientific framework had become since the time of Newton. Not only is the world no longer completely deterministic and limited to the atomic domain, the recent advances in physics have become so dependent on the mathematical formalism that it is impossible to render it intelligible in more familiar, pictorial, or visualizable concepts. Perhaps an exaggeration, but in 1992 Weinberg skeptically claimed like Einstein in the EPR article that

quantum mechanics by itself is not a complete physical theory. It tells us nothing about the particles and forces that may exist. Pick up any textbook on quantum mechanics; you find as illustrative examples a weird variety of hypothetical particles and forces, most of which resemble nothing that exists in the real world, but all of which are perfectly consistent with the principles of quantum mechanics. . . . Most of these theories can be logically ruled out because they would entail nonsense like infinite energies or infinite reaction rates.¹¹⁷

Yet perhaps influenced by the constant references to the experimental confirmation of new discoveries and explanations, I found that most of the physicists at the time were reminiscent of John Trowbridge who had discouraged students at the beginning of the twentieth century from pursuing graduate work in physics believing that nearly everything of importance had been explained. In the latter decades of the century most physicists thought that the final answers would be found in the near future. As Harald Fritzsch, a coworker of Gell-Mann’s, wrote in 1943 in the original German then translated into English in l983 with no retraction:

Today we can state unequivocally that the physics of the atom is understood. A few details need to be cleared up, but that is all. . . . Important and fascinating discoveries have been made in high energy physics, especially since 1969, and today it appears that physicists are about to take the important leap toward a complete understanding of matter.¹¹⁸

Also in his inaugural lecture in April 1980, titled “Is the End in Sight for Theoretical Physics?” when he assumed the Lucasian Chair in physics at Trinity College at Cambridge University, Stephen Hawking, the world’s most famous cosmologist, had the following read (because he has amyotrophic lateral sclerosis):

In this lecture I want to discuss the possibility that the goal of theoretical physics might be achieved in the not-to-distant future, say, by the end of the century. By this I mean that we might have a complete, consistent, and unified theory of the physical interactions which would describe all possible observations. Of course one has to be very cautious about making such predictions. . . . Nevertheless, we have made a lot of progress in recent years and . . . there are some grounds for cautious optimism that we may see a complete theory within the lifetime of those present here.¹¹⁹

In fairness, owing to developments in physics since then, he has lately rescinded his statement. In his recent book previously referred to, The Grand Design, written with Leonard Mlodinow, Hawking describes the cosmological theory of “multiuniverses,” which would contain a vast number of alternate universes whose laws of nature would be very different from ours, thus making a final theory extremely difficult or unlikely.¹²⁰ Still, as Johnson states in Strange Beauty:

Whatever one’s philosophical inclinations, it was hard not to be in awe of the Standard Model. Discovery or invention, it was a work of art. Whether it was the art of nature or the art of human kind could never be known for sure. But it was pleasing to think that humans, on their tiny planet, with their blinkered senses and animal brains, could weave observation and imagination into such a powerful theory. (p. 296)

Before concluding this discussion of the accomplishments of the second revolution I should mention the accurate discovery of the age of the universe since the Big Bang. Hubble had detected the recession of the galaxies from the earth thereby indicating the expansion of the universe, and devised an equation to calculate the rate of the recession as “Ho = v/d (where Ho is the constant, v is the recessional velocity of a flying galaxy, and d its distance away from us).”¹²¹ Based on his formula he calculated the age of the universe to be “about two billion years old.” It wasn’t until “February 2003 that NASA and the Goddard Space Flight Center, using a new type of satellite called the Wilkinson Microwave Anisotropy Probe, announced the age of the universe as 13.7 billion years . . .” (pp. 169–70). Just recently the European Space Agency, using their Planck telescope, determined the age of the universe to be 13.8 billion years. It was in l953, after many other unsuccessful efforts, that Clair Patterson by measuring the amount of radioactive decay of uranium to lead in ancient earth rock crystals, determined the age of the earth to be about “4,550 million years (plus or minus 70 million year)—a figure that stands unchanged 50 years later . . .” (p. 157).