CHAPTER FIVE
HEALTH INEQUALITIES: MEASUREMENT AND DECOMPOSITION
Sam Harper and John Lynch
Since the prior edition of this chapter (Harper and Lynch 2006), the literature on measuring and monitoring health inequalities has exploded. The combination of new data sources, particularly in low- and middle-income countries (e.g., Hosseinpoor 2013; de Walque and Filmer 2013), and widespread international concern regarding social determinants of health (WHO Commission on Social Determinants of Health 2008) has led to a wealth of new studies providing quantitative estimates of social inequalities in health. The raft of new studies suggests continued research and policy interest in understanding and reducing health inequalities. We maintain the basic premise of our earlier chapter that reliable and valid measurement of progress toward reducing health inequalities, if it is to be of value in research and policy-making, requires a framework for conceptualizing and measuring inequalities in health (Sen 2002; Asada 2007).
In this chapter we focus on reviewing ways of measuring health inequalities—that is, observable differences in health among individuals of different social groups. We also show that measures of inequality inherently reflect, to a greater or lesser extent, different ethical and value judgments about what aspects of health inequality are important to capture. Thus it is worthwhile to restate that any choice of health inequality statistic implicitly or explicitly reflects a choice about what is important to measure (Sen and Foster 1997; Asada 2007), the consequences of which can strongly affect conclusions about the magnitude of, and trends in, health inequalities (Harper et al. 2010). It is therefore important to understand the advantages and disadvantages of different methods for measuring health inequalities and how the measures chosen reflect ethical conceptualizations and concerns about what constitutes health inequality and which aspects of inequality we are trying to capture. This chapter does not address the important and fundamental question of how we should measure the social position of individuals, a question dealt with in detail elsewhere in this volume.
Issues
Choosing a measure (or measures) of health inequality necessarily involves the consideration of a number of important conceptual, pragmatic, and technical issues—various measures of inequality differ in how they incorporate the issues outlined in this section, and users and consumers of health inequality statistics should strongly consider what aspects of inequality they consider to be important. More importantly, it should be emphasized that many measures of inequality contain implicit assumptions about certain aspects of inequality (how different individuals or social groups are weighted, for example), and these implicit assumptions can have important consequences for estimating the magnitude of inequality and how it may change over time (Sen and Foster 1997; Harper et al. 2010).
Total Inequality versus Social Group Inequality
One important distinction is between measuring total inequality, or total variation in health, and measuring inequality between social groups. The former involves measuring the univariate distribution of health or disease across all individuals in a population without regard for any other characteristic, whereas the latter involves measuring average health differences between individuals from different social groups. Arguments for measuring total inequality largely focus on its utility for cross-national comparisons where social group definitions may not be standard or transportable across environments (Murray, Gakidou, and Frenk 1999; Gakidou, Murray, and Frenk 2000). This may seem at odds with our notion of why we are measuring health inequality in the first place, as a great deal of attention is focused on inequality between normatively important social groups (Braveman, Krieger, and Lynch 2000). However, a deeper understanding of the overall task of measuring variation in population health requires an appreciation of the concept of total health inequality. It is likely that the amount of health inequality between social groups that we often seek to measure is relatively small compared with the total inequality that exists between individuals in a population (Davey Smith 2011).
Figure 5.1 shows the average body mass index (BMI) for three education groups in the 1988–94 US National Health Nutrition and Health Examination Survey (NHANES). It is clear that there is a gradient of decreasing BMI with increasing education when we compare average BMI across education groups; however, the kernel density plots of BMI in each education group show that there is far greater variation in BMI within education groups than between them. Thus, basing our measure of health inequality on between-group average differences will not capture very much of the total health inequality among individuals. This is not in itself problematic, but it should be understood, and is the reason indicators of total health inequality can be informative. For example, a focus on interventions on the “high-risk” social group (those with the lowest education) will, in practice, only target a very small proportion of those at high risk, because high-risk individuals exist in every educational group. However, it is also true that measures of total health inequality may mask substantial social group inequalities (Asada and Hedemann 2002), and there is no necessary relationship between the extent of total inequality and the extent of between-social-group inequality. Thus far, the evidence seems to indicate that total inequality and social group inequality measure different aspects of population health (Houweling, Kunst, and Mackenbach 2001), where total inequality contains a large stochastic component driven by individual variations but social group inequality captures systematic social group differences in health experience, albeit with large variations within those social groups.
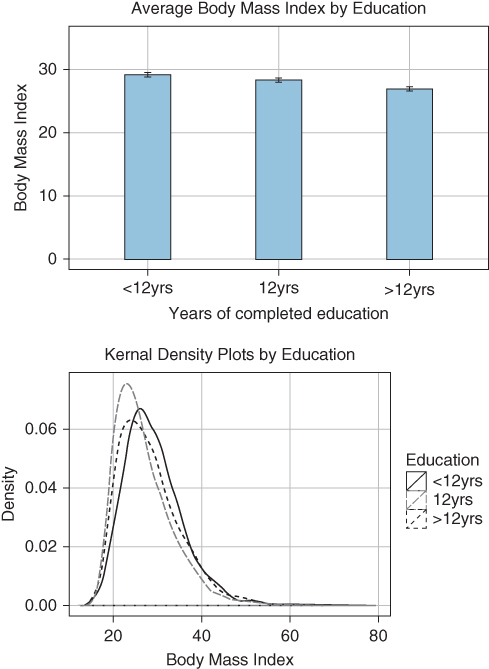
FIGURE 5.1 AVERAGE BODY MASS INDEX AND KERNAL DENSITY ESTIMATES BY YEARS OF COMPLETED EDUCATION FOR WOMEN AGED 25 TO 64
Source: Authors' calculations from US National Health and Nutrition Examination Survey, 1988–1994.
Simple versus Complex Inequality Measures
As we will try to emphasize throughout this chapter, there is often no single “best” choice for a measure of inequality. Researchers should consider the question at hand and the potential audience for results. One consideration should be the potential trade-off between simplicity and depth of assessment. In some cases there may be little benefit to using a complex summary measure of inequality. Figure 5.2 shows the proportion of eight US race-ethnic groups under age 65 with health insurance from 1998 to 2009. Consider the inequality in health insurance coverage between non-Hispanic blacks and whites in 2000 and 2009. Has there been progress? We could calculate the difference between the two groups in 2000, which was 7 percentage points, and compare that to the difference in 2009, which was 8 percentage points. The gap therefore increased by 1 percentage point (ignoring precision). For just two groups, tracking inequality is relatively straightforward.
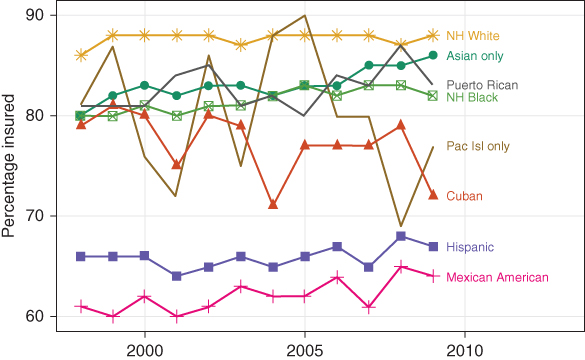
FIGURE 5.2 PROPORTION OF INDIVIDUALS UNDER AGE 65 WITH HEALTH INSURANCE, 1998–2009, BY RACE-ETHNICITY
Source: Authors' calculations from US National Health Interview Surveys.
However, we may want to know how much health inequality exists across all race-ethnic groups and how this has changed over time. If we consider data more representative of US diversity, the sheer number of comparisons makes using simpler measures much more difficult. For example, if we tried to use pairwise measures of inequality, this leads to a large number of indicators to track over time. The large number of possible comparisons hinders effective communication and makes summary measures of inequality appealing.
Absolute and Relative Inequalities
Inequality is an inherently relational concept (Temkin 1993) and one important consideration is scale. Normally we discuss inequality measurement on a relative or absolute scale, but really both are relative measures—one scale expresses the relation between the two quantities being compared through the algebra of division, the other through subtraction. The use of different scales (e.g., relative risk ratios or absolute risk differences) is important because they can provide different perspectives, especially when monitoring changes over time. Figure 5.3 shows the percentage of children under 5 with stunted growth in the richest and poorest quintiles across several Latin American countries (Belizán et al. 2007). Which country has the largest rich–poor inequality in childhood stunting? If we take the relative ratio of poor to rich, then Brazil has the largest inequality 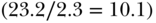 but if we consider the absolute difference then Guatemala has the largest inequality
but if we consider the absolute difference then Guatemala has the largest inequality 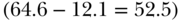 . Clearly, both measures are correct and the answer depends on whether we emphasize relative or absolute aspects of inequality.
. Clearly, both measures are correct and the answer depends on whether we emphasize relative or absolute aspects of inequality.
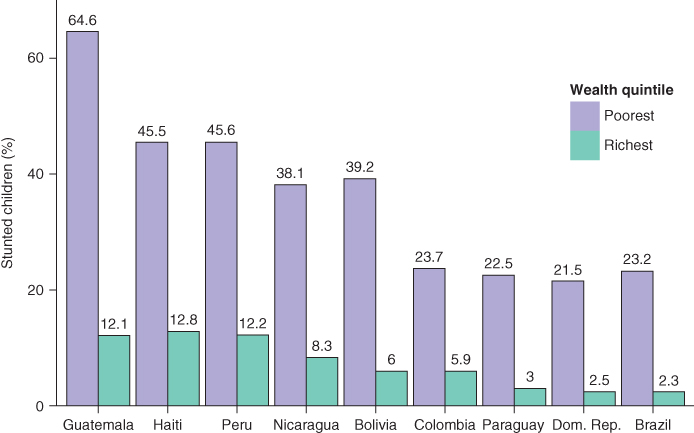
FIGURE 5.3 PERCENTAGE OF STUNTED CHILDREN FOR POOREST AND RICHEST WEALTH QUANTILES, SELECTED COUNTRIES
Source: Belizán et al. (2007)
Figure 5.3 illustrates the possibility that one might arrive at different conclusions about the magnitude of “inequality” depending on the measure selected, and this issue becomes particularly important in the context of monitoring inequality trends. Because there are often factors other than social group status that influence trends in health for the whole population, relative and absolute inequalities may diverge over time. There are many examples of how this can happen (e.g., Moser, Frost, and Leon 2007; Houweling et al. 2007; Ramsay et al. 2008; Regidor et al. 2009; Harper et al. 2010; Charafeddine et al. 2013), and Figure 5.4 shows two situations where simple absolute and relative measures of inequality will (indeed, must) diverge. In the left panel outcomes decrease at the same absolute rate for both advantaged and disadvantaged groups. Because the same absolute decline will be proportionally smaller in a group with higher baseline levels, absolute inequality will be identical but relative inequality will increase. Similarly, the same relative decline in two groups with different starting positions will necessarily lead to decreasing absolute inequality and constant relative inequality. Both relative and absolute measures are “correct” and authors would do well to report both measures, though it appears that most social epidemiology studies continue to privilege relative inequality measures (King, Harper, and Young 2012).
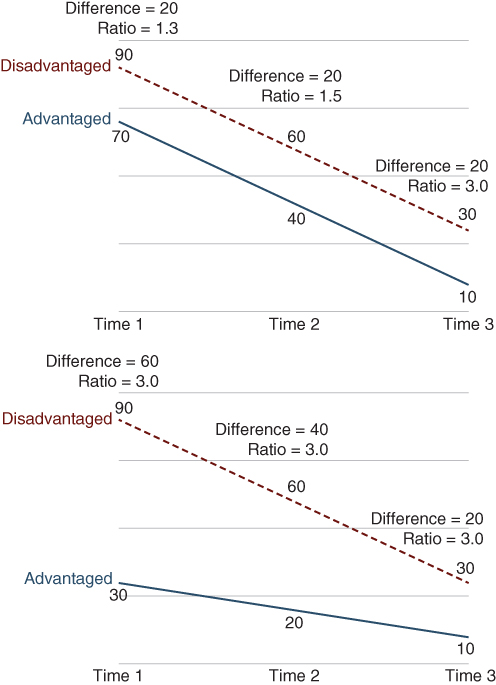
FIGURE 5.4 DIVERGING SCENARIOS FOR ABSOLUTE AND RELATIVE INEQUALITY TRENDS
Reference Groups
Inequality—defined literally as “difference”—implies a comparison group (that is, different from what?). Thus, another important issue in choosing inequality measures is defining the reference group. Different definitions of inequality often imply different comparison groups, and thus the answer one would get about the extent and patterning of inequality may differ depending on the groups compared. For example, in Figure 5.3, should we compare the poor in Guatemala to the poor in Dominican Republic? Or to the rich in Guatemala? Or the rich in Brazil? Or to the average within each country, or across all countries? There is no “correct” reference group, but several choices are possible, and it is perhaps most important to make the rationale for the choice of reference group clear.
One logical reference group might be the population average, where the inequality measure reflects the gap between the health of different social groups and the population average. Although one potential disadvantage of using the population average is the fact that it changes over time, it is an intuitive and often explicit norm used when discussing health inequalities. One might also measure inequality as a difference between each social group compared with the healthiest group. This is similar to the concept of shortfalls (Sen 1992; Erreygers 2009a), where it is implicitly assumed that every social group has the potential to achieve the health of the best-off group. One potential problem with this approach is when the “best-off” group is a small proportion of the population; rates in that group can be unstable, so wide swings in inequality could be recorded that are simply due to the instability of the rate in the comparison group (Keppel, Pearcy, and Kleen 2004). It is also possible to measure inequalities by comparison with all those individuals or groups better off than a particular group or person. The prior three reference groups are inherently relative as they change over time, which may make assessments of trends in inequalities challenging if using pairwise comparisons. One other possibility would be to use a fixed target or goal as the reference point from which to measure difference. One advantage of a fixed or target rate is that the reference level does not change over time unless a new target is adopted. More recent work has aimed to develop indicators that may be invariant to which reference group is chosen Talih (2013).
Number of Social Groups
Many empirical studies measure health inequality by comparing the extreme groups, but it is worth asking whether the measure of inequality should include information from all social groups (that is, the entire population), especially when the two groups at the extreme ends of the social distribution may only reflect the health of a small fraction of the total population. Additionally, although there are good reasons for focusing attention on specific comparisons (e.g., to investigate racial discrimination), such pairwise comparisons do not quantify the inequality across all social groups, which is precisely the goal of initiatives to reduce or eliminate health inequalities. Despite the utility of measuring inequalities between two groups, pairwise comparisons may conceal important heterogeneity and make the situation in other social groups invisible, thus providing a limited view in monitoring progress toward eliminating health inequalities across all social groups.
Population Size
Should the inequality measure incorporate the size of the groups being compared? Should it matter that some social groups comprise a very small proportion of the population? Although this may seem relatively non-controversial, it has important implications for monitoring inequalities and is another case where a statistical choice reflects an ethical choice (Firebaugh 2003). For example, Figure 5.5 shows two hypothetical societies with three social groups that have identical levels of health, but vary widely in their sizes. In Society 1 all three groups are identical in size, but in Society 2 the group with the lowest health (B) is a much larger fraction of the population. If we measure the inequality in health and ignore population size, these two societies will have identical inequality and Group B individuals in Society 2 will receive less weight than individuals in Groups A or C. It is thus important to ask whether we want this unequal weighting of individuals reflected in our inequality measure. On the one hand, weighting groups by population size allows for consideration of social group changes over time, and we also typically count individuals equally when measuring average health. On the other hand, there may be a good reason to argue that, regardless of the number of individuals, each of these social groups is normatively important, and one should not discriminate against a particular group simply because it is small. As with some of the other issues discussed above, there is no right or wrong answer to these questions, but they can have strong implications for measurement. For example, whether life expectancy inequality across US counties is increasing or decreasing depends on whether or not we weight counties by population size (Ezzati et al. 2008; Harper et al. 2010).
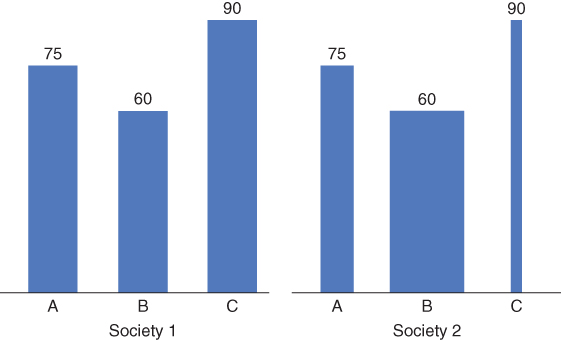
FIGURE 5.5 HYPOTHETICAL LIFE EXPECTANCY FOR THREE SOCIAL GROUPS WITH VARYING POPULATION SIZES IN TWO DIFFERENT SOCIETIES
Distributional Sensitivity
One of the major reasons for the increasing focus on health inequalities is that some kinds of individuals or the members of some social groups are healthy, whereas other kinds are sick. It is the normative distinction between the kinds of healthy or unhealthy individuals that drives concern about health inequalities. For instance, we may be particularly concerned about ill-health in some socially disadvantaged groups (e.g., the homeless or the unemployed) more than in others (Sen 2002; Wagstaff 2002). Not all inequality measures are able to reflect this ethical position. Similarly, all else being equal, if we would prefer a 10% improvement among those with the worst health rather than the same improvement among those with average health, then it would be advantageous if our measure of inequality could reflect this. This relates to the idea of the “principle of transfers” (Pigou 1912; Dalton 1920; Shorrocks and Foster 1987; Sen and Foster 1997). The idea maintains that, ceteris paribus, a transfer of income from a richer to a poorer person should result in a decrease in the inequality measure. Health is obviously not directly transferrable, but in the context of evaluating measures of health inequality one may consider that if the health of every individual remains the same, but a single “healthier” person becomes less healthy and a previously “less healthy” person's health improves, the measure of health inequality should decrease (Illsley, Le Grand, and Williams 1986). The extent to which different inequality measures reflect this principle differs, and analysts should consider the implications of such differences when evaluating inequality.
Decomposability
Decomposability as a property of statistical measures is common to both economics and epidemiology. In economics this typically refers to the ability to decompose a measure of inequality by income source, or by population subgroup (Sen and Foster 1997; Fortin, Lemieux, and Firpo 2011), which allows one to garner information about the sources of total inequality differences across two populations. In public health, decomposition often is used to capture differences in summary rates (Kitagawa 1955), but a number of recent papers have extended the idea of decomposition toward understanding health inequalities (e.g., Wagstaff, van Doorslaer, and Watanabe 2003; O'Donnell et al. 2007).
Positive versus Negative Outcomes
Somewhat related to the issue of absolute versus relative inequality is the nature of the outcome variable. Certainly a variety of continuous, categorical, or (commonly) binary outcomes may be of interest, but when the health variable under consideration is bounded (e.g., between 0 and 1, or 5 ordered categories), it is consequential for measuring inequality whether we focus on attainments versus shortfalls. For example, Figure 5.3 uses “% stunted” as the outcome but one could just as equivalently use “% not stunted.” How might this change our conclusions about which country has the largest poor–rich inequality? As above, using a shortfall measure (% stunted) Brazil has the largest relative inequality and Guatemala the largest absolute inequality. If we use a measure of attainment (% not stunted) Guatemala still has the largest absolute inequality, since 87.9% of the rich are not stunted compared to 35.4% of the poor (absolute difference = 52.5%); however, rather than Brazil having the largest relative inequality (97.7/76.8 = 1.27), Guatemala also has the largest relative inequality (87.9/35/4 = 2.48). Moreover, when one considers the percentage of those not stunted all of the relative measures are lower in magnitude because the absolute proportions are much higher. This point has been made many times (Scanlan 2000; Keppel et al. 2005; Houweling et al. 2007; Kjellsson, Gerdtham, and Petrie 2015), but the consequences of this choice, especially for measuring relative inequality, continue to be underappreciated.
Measures
Here we provide a detailed description of a number of measures of health inequality, with a focus on inequality measures that allow for some kind of between-group decomposition. A few additional measures are described in the Appendix.
Measures of Total Inequality
A measure of “total inequality” in health summarizes measured health differences across a population of individuals. Measures of total health inequality do not account for social grouping (e.g., Illsley, Le Grand, and Williams 1986; Gakidou, Murray, and Frenk 2000; Edwards and Tuljapurkar 2005; Nau and Firebaugh 2012) and typically focus on inequality in life expectancy or age at death (e.g., Smits and Monden 2009). They are an important first step in understanding the scope of health variation in a population and have some advantageous properties for monitoring trends, particularly for cross-country comparisons where social groups may not be comparable. They do not, however, inform us about systematic variation in health among population subgroups, which is inherent in many, if not most, ethical concerns about health inequalities (Navarro 2000; Braveman, Krieger, and Lynch 2000; Braveman et al. 2001).
Range
The range simply measures the spread of the entire distribution of health and is easily calculated as:
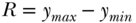
where y is a measure of health. While R clearly captures the spread of the entire distribution of health, it has obvious limitations since it may be heavily influence by extreme values and says nothing about the shape of the distribution between the extremes.
Variance
Rather than simply look at the extremes of the distribution, another class of inequality measures essentially compares each individual's health to the population average, and summarizes some function of those differences as a measure of inequality, commonly known as the variance (V ):
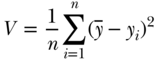
where yi is a measure of health status for individual i,  is the mean health of the population, and n is the number of individuals in the population. One could also take the logarithm of the measure of health, in which case the measure is called the variance of logarithms (VarLog), or one can normalize the health measure by the mean, in which case it is called the squared coefficient of variation (CV 2). More generally, one could consider V to be a special case of a larger group of individual mean difference (IMD) measures given by Gakidou, Murray, and Frenk (2000).
is the mean health of the population, and n is the number of individuals in the population. One could also take the logarithm of the measure of health, in which case the measure is called the variance of logarithms (VarLog), or one can normalize the health measure by the mean, in which case it is called the squared coefficient of variation (CV 2). More generally, one could consider V to be a special case of a larger group of individual mean difference (IMD) measures given by Gakidou, Murray, and Frenk (2000).
Gini Coefficient
Rather than comparing each individual to average health, the Gini summarizes differences in health between all individuals for the entire population. The basic formula for the Gini is given as
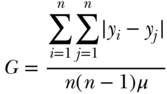
where yi is individual i's health, yj is individual j's health, μ is the mean health of the population, and n is the number of individuals in the population. Formally, the Gini coefficient is derived from the Lorenz curve, which plots the cumulative proportion of population health against the cumulative proportion of the population ranked by health (Figure 5.6 shows a hypothetical Lorenz curve). If health is equally distributed (e.g., the least healthy 50% of the population account for 50% of cumulative health) the curve will be a 45-degree line. Deviations from the “line of equality” increase inequality. For example, the curve shown in Figure 5.6 indicates that the least healthy 67% of the population only account for 50% of the population's health. Equation (3) is equivalent to the ratio of the area between the line of equality and the Lorenz curve to the total area of the triangle beneath the line of equality (Sen and Foster 1997; Hao and Naiman 2010). The Gini ranges from 0 (no inequality) to 1 (where the Lorenz curve is the entire triangle beneath the line of equality).
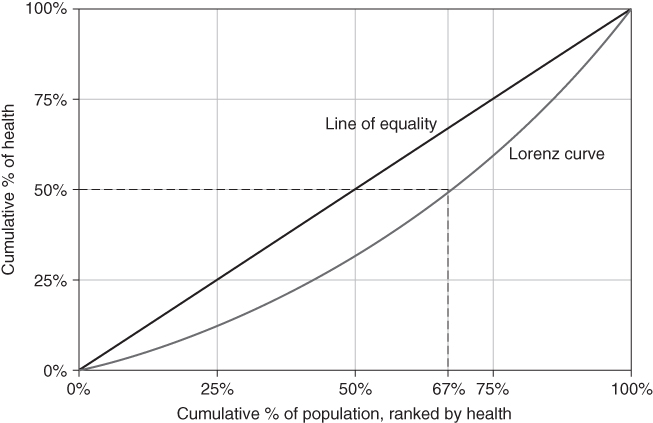
FIGURE 5.6 GRAPHICAL EXAMPLE OF A LORENZ CURVE FOR HEALTH
It should also be noted that Gakidou, Murray, and Frenk (2000) derived a more general measure of inequality that includes the Gini, based on the concept of interindividual differences (IID).
An absolute Lorenz curve may also be drawn using the cumulative absolute contribution to health on the y-axis rather than the cumulative share of health. The absolute Gini has recently been used to demonstrate that relative and absolute global income inequality trends have been diverging (Bourguignon, Levin, and Rosenblatt 2004; Atkinson and Brandolini 2010).
Measures of Entropy
Another class of inequality measures are based on the concept of entropy, derived from information theory (Theil, 1967). Generalized measures of entropy incorporate a parameter that allows for differential sensitivity of the resulting index to different parts of the health distribution (Hao and Naiman, 2010; Cowell, 2011):
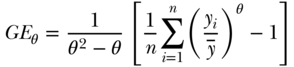
where yi, 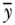 , and n are defined as in Equation (2) above and the inequality aversion parameter θ can be any real number. Two common indices of inequality that are part of the class of entropy-based measures are the Theil index (θ = 1) and the mean log deviation (θ = 0). For individual-level data, total inequality in health/disease y measured by the Theil index and Mean Log Deviation can be written (Hao and Naiman 2010), respectively, as
, and n are defined as in Equation (2) above and the inequality aversion parameter θ can be any real number. Two common indices of inequality that are part of the class of entropy-based measures are the Theil index (θ = 1) and the mean log deviation (θ = 0). For individual-level data, total inequality in health/disease y measured by the Theil index and Mean Log Deviation can be written (Hao and Naiman 2010), respectively, as
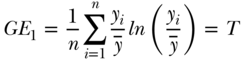
and
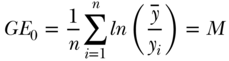
Because the sensitivity parameter θ reflects how sensitive the measure is to the upper tail of the health distribution, the Theil index will be more “top-sensitive” than will M. Both T and M are positive numbers, and values of 0 indicate perfect equality.
Atkinson's Index
The Atkinson index has been used in a number of income and health inequality applications (e.g., Le Grand 1987; Levy, Chemerynski, and Tuchmann 2006; Leibler, Zwack, and Levy 2009; Erreygers 2013), in part because it has many desirable features, including subgroup decomposability and an explicit inequality aversion parameter. The overall index may be written as:
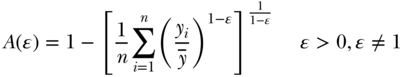
where again 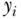 ,
, 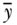 , n are, respectively, individual i's health, average health, and the number of individuals, and ϵ represents an inequality aversion parameter (higher values indicate a stronger preference for equality). Atkinson's index is based on an implied social welfare function, and one of the conceptual ideas inherent in A is “equally distributed equivalent” income, which in our case refers to a measure of health or disease. The index starts with calculating the per capita level of health/disease that would achieve the same equivalent total health as the actual distribution if it were distributed equally to all persons. The index expresses this as a proportion and has an upper bound of 1 (maximum inequality) and a lower bound of 0 whenever outcomes are equally distributed. As with other inequality measures that contain aversion parameters, researchers should recognize the impact of placing additional weight to transfers at the bottom of the distribution when measuring inequality in a “health” variable versus a “disease/risk” variable.
, n are, respectively, individual i's health, average health, and the number of individuals, and ϵ represents an inequality aversion parameter (higher values indicate a stronger preference for equality). Atkinson's index is based on an implied social welfare function, and one of the conceptual ideas inherent in A is “equally distributed equivalent” income, which in our case refers to a measure of health or disease. The index starts with calculating the per capita level of health/disease that would achieve the same equivalent total health as the actual distribution if it were distributed equally to all persons. The index expresses this as a proportion and has an upper bound of 1 (maximum inequality) and a lower bound of 0 whenever outcomes are equally distributed. As with other inequality measures that contain aversion parameters, researchers should recognize the impact of placing additional weight to transfers at the bottom of the distribution when measuring inequality in a “health” variable versus a “disease/risk” variable.
Kolm–Pollack Index
Apart from the variance and the absolute version of the Gini, most other commonly used measures of total inequality focus on relative inequality and the variance does not specifically incorporate an inequality aversion parameter. Though infrequently used in epidemiology, Pollack (1971) and Kolm (1976) derived a measure of absolute inequality that does allow for various levels of inequality aversion. The overall index may be written as
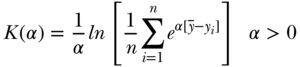
where the parameter 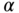 represents the level of inequality aversion (higher levels of
represents the level of inequality aversion (higher levels of 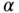 indicate greater aversion to inequality). Like the Atkinson index, the Kolm–Pollack index is a measure based on a social welfare function and the concept of equally distributed equivalents. Maguire and Sheriff (2011) have recently proposed using the Kolm index to measure inequalities in environmental risks, but in general the Kolm–Pollack index has several desirable qualities that merit consideration for measuring health inequalities on the absolute scale.
indicate greater aversion to inequality). Like the Atkinson index, the Kolm–Pollack index is a measure based on a social welfare function and the concept of equally distributed equivalents. Maguire and Sheriff (2011) have recently proposed using the Kolm index to measure inequalities in environmental risks, but in general the Kolm–Pollack index has several desirable qualities that merit consideration for measuring health inequalities on the absolute scale.
Empirical Example
Below we provide a short example using fictitious data to illustrate the differential sensitivity of measures of total inequality to different aspects of inequality. We start with a normally distributed continuous variable (e.g., BMI) with a mean of 27 and a standard deviation of 3.0. We then shift this distribution in several ways to make clear how measures of total inequality respond to distributional changes. We use four alternative distributions: (1) absolute shift (decrease all BMIs by 4 units); (2) proportionate shift (decrease all BMIs by 10%); (3) left-skew shift (greater proportionate shifts at lower BMIs); and (4) right-skew shift (greater proportionate shifts at higher original BMIs) (see Table 5.1). Note that all of the measures of relative inequality (G, T, M, A) are identical for an equal proportionate shift, whereas the measures of absolute inequality (R, V, K) are identical for an equal absolute shift in health. Measures that contain an inequality aversion parameter (A, K) are larger when the inequality aversion parameter increases, and the measures that are distribution sensitive (G, T, M, A, K) respond differently to left- versus right-skew shifts. For example, since V weights deviations equally on either side of the mean, inequality is reduced by similar amounts for left- and right-skew shifts. On the other hand, K is reduced more for right-skew shifts since it places greater weight on transfers from lower to higher levels of health.
TABLE 5.1 IMPACT OF SHIFTS IN THE DISTRIBUTION OF HEALTH ON SELECTED MEASURES OF INEQUALITY
| Measure | Original | Absolute | Proportionate | Left-skew | Right-skew |
Mean 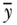 |
27.0 | 23.0 | 24.3 | 24.0 | 29.0 |
| Std Dev. √V | 3.00 | 3.00 | 2.67 | 2.24 | 2.24 |
| Range R | 26.07 | 26.07 | 23.45 | 17.47 | 16.26 |
| Variance V | 8.85 | 8.85 | 7.17 | 5.04 | 5.01 |
| Gini G | 0.0621 | 0.0729 | 0.0621 | 0.0526 | 0.0434 |
| Theil T | 0.0061 | 0.0084 | 0.0061 | 0.0045 | 0.0030 |
| MLD M | 0.0062 | 0.0086 | 0.0062 | 0.0046 | 0.0029 |
| Atkinson A(0.5) | 0.0031 | 0.0043 | 0.0031 | 0.0023 | 0.0015 |
| Atkinson A(2.0) | 0.0125 | 0.0173 | 0.0125 | 0.0094 | 0.0058 |
| Kolm K(0.5) | 2.213 | 2.213 | 1.792 | 1.458 | 1.038 |
| Kolm K(2.0) | 7.532 | 7.532 | 6.364 | 4.887 | 2.090 |

Common Measures of Social Group Inequality
The measures of total variation described in the preceding section have a number of merits, but, for the practicing social epidemiologist, many analyses are specifically focused on social group differences in health, as indeed are many initiatives to reduce health inequalities. Below we provide detail for measures (some of which are based on measures of total inequality) commonly used in the epidemiologic literature. Many of the measures described below are calculated (along with bootstrapped and Taylor series standard errors) by free software available from the US National Cancer Institute (National Cancer Institute, 2013).
Pairwise Comparisons
Simple comparisons of some health indicators between two groups in a population (so-called pairwise comparisons) are one of the most straightforward ways to measure health inequalities. Pairwise comparisons continue to be the workhorse of much of the social epidemiology literature, but in many cases such analysts are interested in adjusting for factors such as age or gender. This may be done straightforwardly using stratified tabular analysis, but most modern analyses use regression modeling, for example, some specification such as
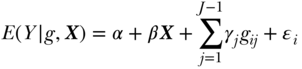
where E(Y ) is the expected outcome, i indexes individuals, j indexes social groups, X is a vector of covariates, 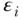 an individual error term, and the coefficient γj expresses the difference between group gj and the reference group. Equation (9) is a linear model and would provide estimates of absolute differences on the linear scale, but non-linear transformations of Equation (11) (e.g., binomial, logistic) would typically yield exponentiated coefficients
an individual error term, and the coefficient γj expresses the difference between group gj and the reference group. Equation (9) is a linear model and would provide estimates of absolute differences on the linear scale, but non-linear transformations of Equation (11) (e.g., binomial, logistic) would typically yield exponentiated coefficients 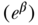 that measure relative inequality (ratios of risks/odds/prevalences).
that measure relative inequality (ratios of risks/odds/prevalences).
Average Social Group Differences
Given a set of measures of health or disease across a set of J social groups, several measures have been derived for summarizing those differences (Hosseinpoor 2013), in addition to those measures of total inequality that also allow for between- and within-group decomposition (discussed below). The main choices for analysts in this case are: (1) whether to measure absolute or relative differences; (2) how to weight the differences; and (3) the reference group. The basic formula for the absolute mean difference of group rates is
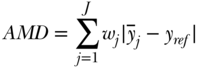
where j indexes social groups, wj is the weight attached to group j, 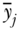 is the average health/disease in group j, and yref is the rate of health/disease in the reference group. For a population-weighted index the weight wj is defined as the population share pj = nj/n, and for an unweighted index one just takes the simple average of differences (i.e., wj = 1/J). The reference population can take on any value, but common values include the population average (yref =
is the average health/disease in group j, and yref is the rate of health/disease in the reference group. For a population-weighted index the weight wj is defined as the population share pj = nj/n, and for an unweighted index one just takes the simple average of differences (i.e., wj = 1/J). The reference population can take on any value, but common values include the population average (yref = 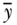 ), the group with the best health, or even a fixed reference value. For example, Hosseinpoor and colleagues (2012) used AMD to study shortfalls in life expectancy across countries from 1950 to 2010.
), the group with the best health, or even a fixed reference value. For example, Hosseinpoor and colleagues (2012) used AMD to study shortfalls in life expectancy across countries from 1950 to 2010.
Equation (10) summarizes absolute differences in group rates, but one may easily calculate a relative version using ratios, which we will call the relative mean difference:
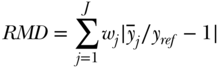
The RMD idea dates back to Dalton (1920), but is generally criticized as an inequality measure because the index is not sensitive to transfers at different parts of the distribution. More recently, Pearcy and Keppel (2002) introduced the index of disparity (ID), which is similar to RMD but is not weighted by group size (i.e., wj = 1/J) and uses the group with the best health as the reference population.
Between-Group Variance
The variance can also be easily decomposed into between-group and within-group components. The between-group part is calculated by assigning individuals within each group (e.g., rich and poor) the average health of their respective groups, and taking the variance of that distribution of groups (this is essentially equivalent to what the variance would be if there was no inequality within social groups); and the within-group part is calculated by calculating the variance separately for each social group (e.g., rich and poor) and taking a weighted average of those variances, with the weights equal to the share of total observations in each group (Sen and Foster 1997; Chakravarty 2001; Hao and Naiman 2010):
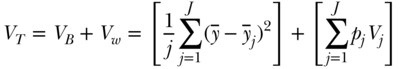
where VB and VW are, respectively, the between-group and within-group variance, 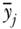 is the mean health of the jth group, and pj and Vj are, respectively, the population fraction and within-group variance for each social group j. In the context of analyses focused only on estimating the magnitude of inequality between groups, the first bracketed term on the right-hand side of Equation (12) may be used to measure inequality between groups and is sometimes called the between-group variance (e.g., Harper et al. 2008). The Variance does not have an explicit inequality aversion parameter, but it does incorporate an implicit weighting by squaring differences and therefore placing a greater weight on larger differences from the average. Some relative forms of the variance, such as the squared coefficient of variation, are also additively decomposable inequality measures, but require adjustments to the weighting scheme for the within-group inequality component (Sen and Foster 1997; Levy, Chemerynski, and Tuchmann 2006; Hao and Naiman 2010).
is the mean health of the jth group, and pj and Vj are, respectively, the population fraction and within-group variance for each social group j. In the context of analyses focused only on estimating the magnitude of inequality between groups, the first bracketed term on the right-hand side of Equation (12) may be used to measure inequality between groups and is sometimes called the between-group variance (e.g., Harper et al. 2008). The Variance does not have an explicit inequality aversion parameter, but it does incorporate an implicit weighting by squaring differences and therefore placing a greater weight on larger differences from the average. Some relative forms of the variance, such as the squared coefficient of variation, are also additively decomposable inequality measures, but require adjustments to the weighting scheme for the within-group inequality component (Sen and Foster 1997; Levy, Chemerynski, and Tuchmann 2006; Hao and Naiman 2010).
Entropy-Based Measures
When the population of individuals is arranged into J groups, entropy-based measures of inequality may be expressed as the exact sum of two parts: between-group inequality and a weighted average of within-group inequality. For the Theil index we have
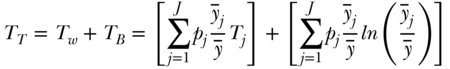
where TB is the between-group Theil index, 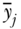 is the average health in group j, TW is the total within-group Theil index, and Tj is the inequality in health within group j. The within-group component (the first term on the right-hand side of Equation (13)) is effectively weighted by group j's share of total health, since
is the average health in group j, TW is the total within-group Theil index, and Tj is the inequality in health within group j. The within-group component (the first term on the right-hand side of Equation (13)) is effectively weighted by group j's share of total health, since 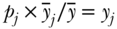 (where yj is the share of total health in group j). The above decomposition of TT also makes it clear that it is possible to calculate between-group inequalities in health without having data on each individual's health status. The only data needed are the proportions of the population in each social group
(where yj is the share of total health in group j). The above decomposition of TT also makes it clear that it is possible to calculate between-group inequalities in health without having data on each individual's health status. The only data needed are the proportions of the population in each social group 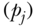 and the ratio of the group's health to that of total population (
and the ratio of the group's health to that of total population (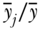 ). As noted above, using the Theil index involves a choice among the various generalized measures of entropy. Thus, an explicit inequality aversion parameter is involved in the selection process, with the statistical formulation of the Theil index placing greater weight at the upper end of the distribution.
). As noted above, using the Theil index involves a choice among the various generalized measures of entropy. Thus, an explicit inequality aversion parameter is involved in the selection process, with the statistical formulation of the Theil index placing greater weight at the upper end of the distribution.
To decompose total M into within-group (MW) and between-group (MB) components the following formula may be used:
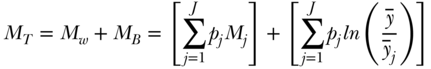
where Mj is the inequality in health within group j and pj is again the social group proportion of the population. The main difference between TB and MB is differential sensitivity to different parts of the health distribution, with the former being more sensitive to the upper (healthier) part of the health distribution and the latter the lower (less healthy) part of the distribution. Additionally, TB is weighted by shares of health in each social group, whereas MB is weighted by shares of population. Thus TB will be somewhat more influenced by groups with larger health ratios (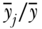 ) whereas MB will be somewhat more influenced by groups with large population shares (pj). It should also be noted that a “symmetrized” between-group entropy index has been developed (Borrell and Talih 2011) to measure between-group inequality that is effectively a weighted average of TB and MB.
) whereas MB will be somewhat more influenced by groups with large population shares (pj). It should also be noted that a “symmetrized” between-group entropy index has been developed (Borrell and Talih 2011) to measure between-group inequality that is effectively a weighted average of TB and MB.
Atkinson Index
The Atkinson index is not strictly additively decomposable. However, it may be usefully decomposed into a between-group component, a within-group component, and a residual term that is minus the product of the between and within components (Levy, Chemerynski, and Tuchmann 2006; Hao and Naiman 2010). By replacing each individual's health with the average of the value for their social group, one can use the Atkinson index to measure between-group inequality:
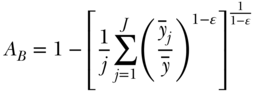
where 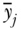 now represents the average health of group j. The formula for the within-group component is somewhat more complicated than for the entropy-based measures above, and is given by Cowell (2011, p. 159).
now represents the average health of group j. The formula for the within-group component is somewhat more complicated than for the entropy-based measures above, and is given by Cowell (2011, p. 159).
Kolm Index
Kolm's index of absolute inequality may also be decomposed into within- and between-group components (Blackorby, Donaldson, and Auersperg 1981). Parker (1999) gives the formula as
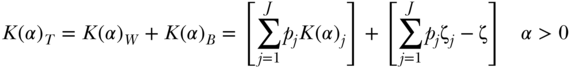
where again 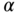 is a non-negative inequality aversion parameter. The between-group component is based on the sum of social group-weighted equally distributed health for each subgroup
is a non-negative inequality aversion parameter. The between-group component is based on the sum of social group-weighted equally distributed health for each subgroup 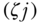 and the overall equally distributed health
and the overall equally distributed health 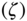 . The formula for the overall equally distributed equivalent income for the Kolm–Pollack index is given by
. The formula for the overall equally distributed equivalent income for the Kolm–Pollack index is given by
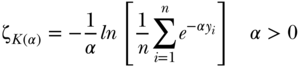
Population Impact Measures
The population attributable risk (PAR) and its relative analog, the PAR% (sometimes called the population attributable fraction, or PAF), are epidemiologic measures used to quantify the population health burden associated with differential health between groups. Although typically applied to groups defined by their exposure status (for example, comparing smokers with non-smokers), they have also been applied to social groups as a measure of health inequality. These measures attempt to quantify how much the health of the total population would improve if all social groups had the rates of health in the best-off social group, an empirical expression of a common argument for reducing health inequalities (Galea et al. 2011; Charafeddine et al. 2013). Because a number of assumptions underlie the interpretation of attributable fractions (Levine 2007), not the least of which is causality, analysts should be clear that such measures are descriptive. Moreover, care should be taken when calculating adjusted impact measures (Miettinen, 1974; Benichou 2001) as the epidemiologic literature is full of examples of the inappropriate use of adjusted estimators (Rockhill, Newman, and Weinberg 1998; Darrow and Steenland 2011; Flegal 2014).
Socioeconomic Rank-dependent Measures of Inequality
For ordinal measures of social status (whether individual or group level), several other measures of health inequality have been developed and are now used extensively in monitoring socioeconomic inequalities in health. All of the indices below rely on ranking individuals (or groups) across the dimension of socioeconomic position. Below in Table 5.2 we show how the ranking variable is calculated using grouped data (it is analogous for individual data, but individual-level measures of socioeconomic position are less common). For a population of 1000 individuals and five education groups, one first calculates the range that each group occupies in the cumulative distribution. The rank variable is then calculated as the midpoint of this range for each group. It should be noted that this kind of ranking variable will be insensitive to the qualitative nature of the grouping. Thus users should be clear that such measures are based on relative rankings. However, one advantage of this relative ranking method is that the rank-dependent measures easily incorporate changes in the distribution of the socioeconomic variable over time, which may be valuable in the context of measuring trends.
TABLE 5.2 CALCULATION OF GROUP-BASED RANKING IN THE CUMULATIVE DISTRIBUTION OF EDUCATION
| Group | Population (%) | Cumulative (%) | Range | Midpoint (rank) |
| None | 0.12 | 0.12 | 0.00–0.12 | 0.06 |
| <Primary school | 0.15 | 0.27 | 0.12–0.27 | 0.19 |
| Primary school | 0.27 | 0.54 | 0.27–0.54 | 0.40 |
| Secondary school | 0.16 | 0.70 | 0.54–0.70 | 0.62 |
| >Secondary | 0.30 | 1.0 | 0.70–1.00 | 0.85 |
Concentration Index
The Concentration Index (Kakwani, Wagstaff, and van Doorslaer 1997) is conceptually similarly to the Gini index, but it results from a bivariate distribution of health and social group ranking, and thus is not a measure of total inequality but measures the relationship between socioeconomic ranking and health (Wagstaff and van Doorslaer 2004). The Concentration Index is derived from a concentration curve, where the population is first ordered by social group status (rather than by health status, as for the Gini index) and the cumulative percentage of the population is then plotted on the x-axis against health or ill-health on the y-axis. When the y-axis is the share of ill health, this results in the relative concentration curve; however, an absolute concentration curve may also be derived by plotting the cumulative share of the population against the cumulative amount of ill-health (i.e., the cumulative contribution of each subgroup to the mean absolute level of health in the population). Figure 5.7 shows relative and absolute concentration curves for current smoking for Brazil and Dominican Republic in 2002. Notice that the absolute curves reflect the fact that smoking is more common in Brazil.
FIGURE 5.7 RELATIVE AND ABSOLUTE HEALTH CONCENTRATION CURVES FOR DAILY SMOKING IN BRAZIL AND DOMINICAN REPUBLIC, 2002
Source: Authors' calculations from the World Health Surveys.
A substantial number of theoretical and empirical papers have been written on the Concentration Index (C) since the first edition of this chapter. In particular, Erreygers (Erreygers 2009b, 2009c; Erreygers and Van Ourti 2011b) and Wagstaff (2009, 2011) have had a spirited and productive debate on the technical aspects of what can and cannot be measured using the concentration index. If we consider a population of n individuals who have a continuous, unbounded, ratio-scale measure of health y (e.g., height), we can write the mean health of the population as 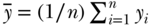 . For individual data the concentration index can be written as
. For individual data the concentration index can be written as
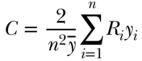
where Ri is the relative rank of person i in the cumulative distribution of the population ranked by the socioeconomic variable (as in Table 5.2). This is a measure of relative inequality, and C ranges from +1 (health completely concentrated among the rich) to –1 (health completely concentrated among the poor), with 0 indicating no inequality (note that the signs would be reversed when measuring disease instead of health). C does not have a straightforward interpretation, but Koolman and van Doorslaer (2004) have shown that multiplying C by 75 gives the proportion of the outcome that would need to be linearly redistributed from the rich to the poor (in the case of pro-rich inequality) in order to arrive at a value of 0 for C. As noted above, C measures relative inequality, but multiplying C by the mean of the health variable (y) leads to an absolute (sometimes called a “generalized”) version of the index:
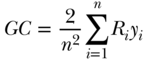
Equations (18) and (19) are written in the context of individual level measures of socioeconomic position, but it is more common to have measures at the group level. In the context of group data, one can also write C as
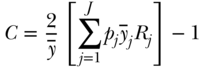
where again  is average health, pj is the proportion of the population in group j,
is average health, pj is the proportion of the population in group j, 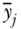 is group j's health, and Rj is the group's average socioeconomic rank, calculated as
is group j's health, and Rj is the group's average socioeconomic rank, calculated as 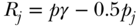 , where
, where 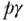 is the cumulative proportion of the population up to and including group j. It should be noted that when group measures of socioeconomic position are used, the value of C may be affected by how the health variable is sorted, and random sorting within socioeconomic groups prior to calculation is recommended (O'Donnell et al. 2007; Chen and Roy 2009).
is the cumulative proportion of the population up to and including group j. It should be noted that when group measures of socioeconomic position are used, the value of C may be affected by how the health variable is sorted, and random sorting within socioeconomic groups prior to calculation is recommended (O'Donnell et al. 2007; Chen and Roy 2009).
A number of important limitations to C have been reported in a series of recent papers. Most important for health researchers is probably the fact that the bounds of C may differ depending on the nature of the health variable under investigation. Wagstaff (2005) first noted that when the health variable is binary, the bounds of C are constrained by the mean, and rather than ranging from 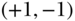 , instead range from
, instead range from 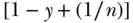 to
to 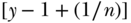 . Thus, for example, if the overall prevalence of a binary outcome is 0.4, the minimum and maximum values of C are effectively (0.6, –0.6). More generally, for an outcome variable that takes on respective maximum and minimum values of bx and ax, Wagstaff (2009) recommended a measure of relative inequality that essentially divides C by its feasible maximum:
. Thus, for example, if the overall prevalence of a binary outcome is 0.4, the minimum and maximum values of C are effectively (0.6, –0.6). More generally, for an outcome variable that takes on respective maximum and minimum values of bx and ax, Wagstaff (2009) recommended a measure of relative inequality that essentially divides C by its feasible maximum:
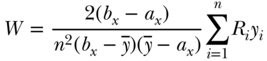
and Erreygers (Erreygers 2009b; Erreygers and Van Ourti 2011a) derived a formula for measuring absolute inequality in the context of bounded outcomes:
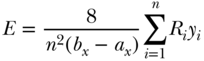
A second issue is that in the case of bounded variables the calculation of relative inequality will be affected by whether we talk about inequality in health (h) versus its complement (1 − h). That is, for C and W the measure of inequality will differ whether our outcome is the presence versus absence of disease. Methods for calculating standard errors for C are given by Kakwani, Wagstaff, and van Doorslaer (1997) and O'Donnell et al. (2007), and the latter authors also give a very practical guide (including Stata code) to the calculation and estimation of C using regression.
Finally, like some other inequality measures, the concentration index contains an implied weighting scheme that gives more weight to the health of lower- versus higher-ranked individuals (Wagstaff, 2002). For grouped data one may write the extended formula as
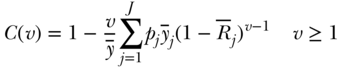
where ν is a parameter that increases the weight placed on the health of lower-ranked groups and the other parameters are defined as in Equation (20). The “standard” index has ν = 2 and leads to respective weights of 2, 1.5, 1, 0.5, and 0 for the health of individuals at the 0th, 25th, 50th, 75th, and 100th percentile of the cumulative distribution according to socioeconomic position. This of course implies a value judgment and users should be aware of the implicit values that come with the use of the “standard” index. Moreover, Erreygers, Clarke, and Van Ourti (2012) have noted that the weighting scheme in Equation 28 is not symmetric with respect to those ranked above versus below the median (except for 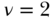 ) and have proposed an alternative “extended” index with symmetric weights. Recently Talih (2015) has also developed a new rank-based index that also includes an inequality aversion parameter.
) and have proposed an alternative “extended” index with symmetric weights. Recently Talih (2015) has also developed a new rank-based index that also includes an inequality aversion parameter.
Slope and Relative Index of Inequality
Another set of rank-based indices are the Slope and Relative Index of Inequality—SII and RII, respectively (Preston et al. 1981; Pamuk 1985). SII and RII are regression-based measures and may be derived by regressing the socioeconomic rank variable (Ri for individuals or 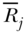 for groups) on the measure of health. The SII, which was introduced by Preston et al. (1981), may be obtained via regression of the mean health variable on the mean relative rank variable:
for groups) on the measure of health. The SII, which was introduced by Preston et al. (1981), may be obtained via regression of the mean health variable on the mean relative rank variable:
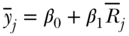
Since the ranking variable varies from 0 to 1, a one-unit change in the ranking variable represents moving from the bottom to the top of the socioeconomic distribution if ranked from low to high, or from the top to the bottom if ranked high to low. Often the latter is more easily interpretable, and both measures are based on the estimated value of health at the bottom versus the top of the distribution, so that 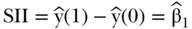 and
and 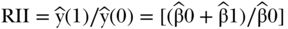 . This version of RII was developed by Kunst and Mackenbach (1995), but Pamuk (1985) earlier defined a version of RII based on dividing SII by the mean health in the population (e.g.,
. This version of RII was developed by Kunst and Mackenbach (1995), but Pamuk (1985) earlier defined a version of RII based on dividing SII by the mean health in the population (e.g., 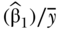 ). Both are valid measures of relative inequality.
). Both are valid measures of relative inequality.
Figure 5.8 shows the observed data and predicted slope for the income-related inequality (based on the income-to-poverty ratio) in current smoking for the United States in 2002. Note that the location of the data points on the x-axis is based on the group's relative rank, whereas the size of each point reflects each group's population share. Because the SII uses the midpoint of the cumulative social group distribution and, because it is based on grouped data and is a weighted index, the weights are the share of the population in each social group. By weighting social groups by their population share, the SII thus is able to incorporate changes in the distribution of social groups over time that affect the population health burden of health inequalities.
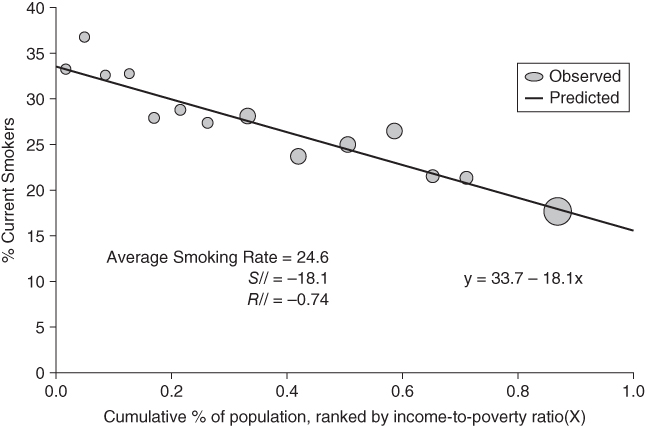
FIGURE 5.8 INCOME-BASED SLOPE AND RELATIVE INDEX OF INEQUALITY IN CURRENT SMOKING
Source: US National Health Interview Survey 2002.
The coefficient 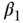 in Equation (24) is the SII, which is interpreted as the absolute difference in health status between the bottom and top of the social group distribution. Thus, the regression equation in Figure 5.8 shows that the absolute difference in the prevalence of smoking across the entire distribution of income is −18.1 percentage points. The RII can be estimated as 2.16, which is the ratio of smoking at the bottom (33.7) versus the top (33.7 – 18.1 = 15.6), or as a 74% proportionate decline. The same regression may also be run on individual data, where Ri would be an individual's relative rank in the social group distribution. In this case the data would be self-weighting and could be estimated by ordinary least squares. Equation (24) is a linear model, but in many cases analysts may prefer to use non-linear models for incidence rates. Additionally, in many cases it may be useful to adjust for other covariates (e.g., age). Recently, Moreno-Betancur et al. (2015) have clarified and formalized the SII and RII models for cohort-based studies. In the context of aggregate event rate data they recommend using multiplicative and additive Poisson models to estimate RII and SII, respectively. For individual-level time-to-event data the RII may be estimated using Cox regression, such as
in Equation (24) is the SII, which is interpreted as the absolute difference in health status between the bottom and top of the social group distribution. Thus, the regression equation in Figure 5.8 shows that the absolute difference in the prevalence of smoking across the entire distribution of income is −18.1 percentage points. The RII can be estimated as 2.16, which is the ratio of smoking at the bottom (33.7) versus the top (33.7 – 18.1 = 15.6), or as a 74% proportionate decline. The same regression may also be run on individual data, where Ri would be an individual's relative rank in the social group distribution. In this case the data would be self-weighting and could be estimated by ordinary least squares. Equation (24) is a linear model, but in many cases analysts may prefer to use non-linear models for incidence rates. Additionally, in many cases it may be useful to adjust for other covariates (e.g., age). Recently, Moreno-Betancur et al. (2015) have clarified and formalized the SII and RII models for cohort-based studies. In the context of aggregate event rate data they recommend using multiplicative and additive Poisson models to estimate RII and SII, respectively. For individual-level time-to-event data the RII may be estimated using Cox regression, such as
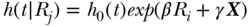
and the estimate of RII given as 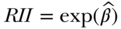 . Again, this expresses the ratio of estimated health for a 1-unit change in the relative ranking variable, conditional on the baseline hazard
. Again, this expresses the ratio of estimated health for a 1-unit change in the relative ranking variable, conditional on the baseline hazard 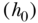 and a vector of covariates X. The SII can also be estimated using an additive hazards model:
and a vector of covariates X. The SII can also be estimated using an additive hazards model:
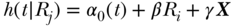
where α0 is an unspecified baseline hazard, X a vector of covariates, and the index is estimated directly as 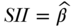 .
.
Decomposition of Inequalities
In many cases we may want to go further than simply measuring inequalities to asking questions such as how much of total inequality occurs between social groups or what factors contribute most to levels or changes in inequality? These are questions about the composition of inequality, and there are several techniques for decomposing inequalities. More detailed treatments of inequality decomposition are provided elsewhere (Mookherjee and Shorrocks 1982; Jenkins 1995; Wagstaff, van Doorslaer, and Watanabe 2003; O'Donnell et al. 2007; Fortin, Lemieux, and Firpo 2011), but we describe below the basic concepts and show some applied examples.
Decomposing Total Inequality by Social Group
For social epidemiologists, decomposition analyses may be interesting for understanding how much of total inequality is “due” to social group status. These decomposition techniques use information on the health of population subgroups, typically by social or demographic characteristics, to decompose the total amount of inequality into “between-group” and “within-group” components. We provide here a brief example of total inequality decomposition using data on BMI by education. We use three education groups (<12 years, 12 years, >12 years) and, to demonstrate how within- and between-inequality can move in different directions, we compare the BMI inequality decomposition in the early 1960s to that from the mid-2000s.
Table 5.3 shows the within/between decomposition of total inequality in BMI for five inequality measures. As is well known, mean BMI increased substantially in the latter twentieth century, as reflected in the mean increase from 25.2 to 28.2 kg/m2. Notably, all of the measures of total inequality increased from the early 1960s to the mid-2000s, both in absolute (V, K) and relative (T, M, A) terms. One can also see the benefit of assessing decomposable inequality measures. Total inequality increased, but this was entirely due to increases in BMI inequality within rather than between education groups. Between-group inequality was roughly 2% of total inequality in the early 1960s, but since has declined to roughly 0.25%. This suggests that the determinants of the increase in BMI inequality are likely to be shared characteristics of all education groups rather than differentially distributed between education groups. Studies using pairwise comparisons or rank-based measures of socioeconomic inequality have also found between-group educational inequalities to be decreasing (Zhang and Wang 2004, 2007; An 2015).
TABLE 5.3 TOTAL, WITHIN- AND BETWEEN-GROUP INEQUALITY IN BODY MASS INDEX BY EDUCATION AND GENDER
| Education | Inequality decomposition | ||||||
| 1959-62 | <12y | 12y | >12y | Total | Within | Between | %Between |
| Population share | 31.6 | 50.2 | 18.2 | ||||
| Mean | 26.2 | 24.8 | 24.5 | 25.2 | |||
| Variance | 26.55 | 21.54 | 15.51 | 22.50 | 22.03 | 0.4820 | 2.14 |
| Theil | 0.019 | 0.017 | 0.013 | 0.017 | 0.017 | 0.0004 | 2.25 |
| Mean Log Deviation | 0.018 | 0.016 | 0.012 | 0.016 | 0.016 | 0.0004 | 2.26 |
| Atkinson(0.5) | 0.009 | 0.008 | 0.006 | 0.008 | 0.008 | 0.0002 | 2.41 |
| Kolm(0.5) | 3.94 | 3.11 | 2.66 | 3.31 | 3.29 | 0.0151 | 0.46 |
| 2004–05 | |||||||
| Population share | 28.6 | 22.0 | 49.4 | ||||
| Mean | 28.7 | 29.4 | 28.6 | 28.8 | |||
| Variance | 55.20 | 46.02 | 44.89 | 48.17 | 48.09 | 0.0810 | 0.17 |
| Theil | 0.029 | 0.026 | 0.026 | 0.026 | 0.027 | 0.0001 | 0.24 |
| Mean Log Deviation | 0.027 | 0.025 | 0.025 | 0.026 | 0.026 | 0.0001 | 0.23 |
| Atkinson(0.5) | 0.014 | 0.013 | 0.013 | 0.013 | 0.013 | 0.0000 | 0.23 |
| Kolm(0.5) | 5.73 | 6.04 | 5.41 | 5.64 | 5.64 | 0.0046 | 0.08 |
Source: Authors' calculations of the 1959–1962 and 2005–2006 US National Health and Nutrition Examination Surveys.
Decomposing Social Group Inequality by Risk Factors
It may also be of interest to understand how social group inequalities in health may be influenced by other factors. For example, we may want to know how much social group inequality may be “explained” by the social distribution of other risk factors for the outcome. Below we provide brief examples of two methods for decomposing social group differences by risk factor.
Decomposing Average Differences Between Social Groups
One question of interest to social epidemiologists is how much of the observed difference in health between two groups is due to particular factors such as demographic differences, risk factors, health service utilization, and so on. Methods for “unpacking” average differences between groups date back to at least Kitagawa (1955), but more formal treatments were given in the early 1970s (Oaxaca 1973; Blinder 1973). Although there are non-parametric methods for decomposing differences between groups (see Fortin, Lemieux, and Firpo 2011), a large literature using regression models has developed. Much of this literature began with trying to quantify the role that discrimination may play in generating wage differences between social groups (Jones and Kelley 1984). Were average wages higher for whites than blacks because whites earned more from a given set of endowments (education, for example) or because blacks and whites differed in the set of factors that were highly predictive of wages? One way of understanding this gap was to estimate a prediction equation for the two groups separately, and then use counterfactual predictions to determine how much of the “gap” was due to differences in average determinants (means) versus differences in the effects of determinants on outcomes (coefficients).
For example, Figure 5.9 shows that hypothetical regression lines fit separately for exposed and unexposed groups, and visually one can see that the average difference in outcome y is potentially a function of both the different slopes and differences in the average values of determinants (xs).
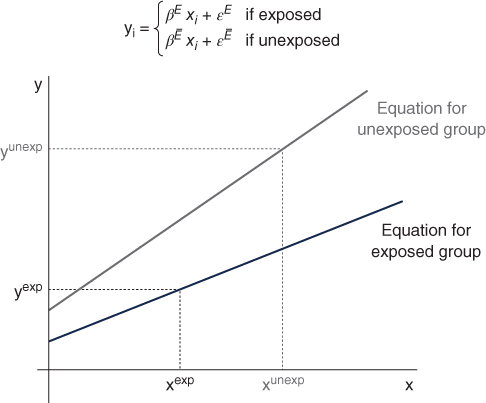
FIGURE 5.9 GRAPHICAL DEPICTION OF BLINDER–OAXACA DECOMPOSITION
These decompositions thus express average differences between groups as a function of differences in coefficients, differences in mean covariates, and an interaction term. Importantly, these can be expressed in several equivalent ways (Jones and Kelley 1984). One can use the coefficients and average covariates of the unexposed group:
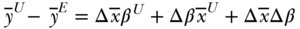
where  is the difference operator and the superscripts U and E refer to unexposed and exposed groups. The first term estimates the component of the health gap that would be diminished if the unexposed group had the average covariates of the exposed group. The second part estimates how much the health of the unexposed group would change if it had the coefficients of the exposed group. The third component estimates how much health would change for the unexposed group if they had the average covariate values of the exposed group and if those covariates impacted health the way they do for the exposed group. The interpretation in Equation (28) is taken from the perspective of the unexposed group, but one could equally use the means and coefficients of the exposed group as the standard:
is the difference operator and the superscripts U and E refer to unexposed and exposed groups. The first term estimates the component of the health gap that would be diminished if the unexposed group had the average covariates of the exposed group. The second part estimates how much the health of the unexposed group would change if it had the coefficients of the exposed group. The third component estimates how much health would change for the unexposed group if they had the average covariate values of the exposed group and if those covariates impacted health the way they do for the exposed group. The interpretation in Equation (28) is taken from the perspective of the unexposed group, but one could equally use the means and coefficients of the exposed group as the standard:
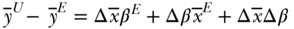
Since these decompositions are simply weighted combinations of coefficients and covariates, other formulations are possible, including using average values of both groups for the covariates, average values of the coefficients for both groups, or using coefficients pooled across both groups (Fortin, Lemieux, and Firpo 2011). In the case where pooled coefficients are used, the interaction component drops out:
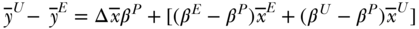
where 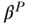 are coefficients from the pooled regression, the first right-hand side term represents the “explained” part due to covariate differences and the second term (in brackets) is often referred to as the “unexplained” part. Because these methods were derived from trying to explain wage discrimination, it is not clear that any set of coefficients for the effect of covariates on health can be considered “standard.” It is generally considered good practice to evaluate the robustness of the decomposition results to alternative weighting schemes. See O'Donnell et al. (2007) and Fortin, Lemieux, and Firpo (2011) for additional details.
are coefficients from the pooled regression, the first right-hand side term represents the “explained” part due to covariate differences and the second term (in brackets) is often referred to as the “unexplained” part. Because these methods were derived from trying to explain wage discrimination, it is not clear that any set of coefficients for the effect of covariates on health can be considered “standard.” It is generally considered good practice to evaluate the robustness of the decomposition results to alternative weighting schemes. See O'Donnell et al. (2007) and Fortin, Lemieux, and Firpo (2011) for additional details.
We provide a simple example of Blinder–Oaxaca decomposition using mean differences in weight for white and black Americans, based on the 1988–1994 NHANES survey. Average weight (kg) was 74.4 for whites, 78.8 for blacks, a difference of 4.4 kg. How much of this differences is accounted for by demographic, socioeconomic, and other behavioral factors?
Table 5.4 shows some evidence of differences between blacks and whites in both covariate means and the association of demographic and risk factors for weight. Table 5.5 shows results of the decomposition analysis, using three possible sets of coefficients (we used Jann's (2008) oaxaca command for Stata, but several other packages are available). The main results show that only a minority (roughly 15–30%) of the black–white difference in weight is attributable to differences in mean covariates between the two groups, the largest component of which is height. Also note that these are “net” effects: both height and age increase weight, so the black excess in height and the black deficit in age contribute in opposite directions. Obviously, the extent to which one may “explain” social group differences hinges on the quality of the regression, and unmeasured factors will of course contribute to the “unexplained” part of the decomposition. A number of other technical details need consideration for any Blinder–Oaxaca decomposition (e.g., the choice of omitted categories can influence results, effect measure modification). In addition, we have focused on linear decomposition but extensions to non-linear models (Fairlie 2005), time-to-event outcomes (Powers and Yun 2009), and quantile regression (Machado and Mata 2005) have been established in recent years.
TABLE 5.4 MEANS AND REGRESSION COEFFICIENTS FOR WEIGHT (kg) FOR COVARIATES
| Covariate means | Regression coefficients | |||||||
| White | Black | White | Black | |||||
| Variable | 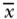 |
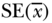 |
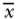 |
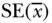 |
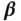 |
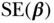 |
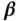 |
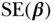 |
| Age | 43.69 | 0.17 | 39.89 | 0.23 | 0.14 | 0.01 | 0.19 | 0.02 |
| Height (cm) | 166.26 | 0.10 | 168.77 | 0.13 | 0.79 | 0.02 | 1.01 | 0.04 |
| Male | 0.48 | 0.00 | 0.45 | 0.01 | 0.85 | 0.41 | −7.58 | 0.73 |
| Education <12y | 0.41 | 0.00 | 0.37 | 0.01 | 0.97 | 0.31 | −0.32 | 0.56 |
| Married | 0.67 | 0.00 | 0.43 | 0.01 | 2.78 | 0.32 | 2.68 | 0.55 |
| Ever smoked | 0.51 | 0.00 | 0.47 | 0.01 | −0.68 | 0.30 | −3.52 | 0.55 |
| Intercept | −65.22 | 3.55 | −94.72 | 6.49 | ||||
Source: Authors' calculations from US National Health and Nutrition Examination Survey, 1988–1994.
TABLE 5.5 COMPONENTS OF THE MEAN DIFFERENCE IN WEIGHT (kg) FOR BLACKS AND WHITES
| Black | Black | White | Pooled | |||
| Weight (kg) | Est. | SE | Est. | SE | Est. | SE |
| White | 74.37 | 0.17 | 74.37 | 0.17 | 74.37 | 0.17 |
| Black | 78.79 | 0.28 | 78.79 | 0.28 | 78.79 | 0.28 |
| Difference | −4.41 | 0.33 | −4.41 | 0.33 | −4.41 | 0.33 |
 due to: due to: |
||||||
| Covariate Means | −1.48 | 0.22 | −0.71 | 0.17 | −0.96 | 0.16 |
| Age | 0.72 | 0.09 | 0.55 | 0.05 | 0.58 | 0.05 |
| Height (cm) | −2.53 | 0.19 | −1.98 | 0.14 | −2.14 | 0.15 |
| Male | −0.19 | 0.07 | 0.02 | 0.01 | −0.04 | 0.02 |
| Education <12y | −0.01 | 0.02 | 0.04 | 0.01 | 0.03 | 0.01 |
| Married | 0.66 | 0.14 | 0.68 | 0.08 | 0.68 | 0.07 |
| Ever smoked | −0.13 | 0.04 | −0.02 | 0.01 | −0.06 | 0.02 |
| Coefficients | −3.70 | 0.32 | −2.93 | 0.35 | −3.45 | 0.31 |
| Age | −1.82 | 0.79 | −1.99 | 0.86 | −1.85 | 0.76 |
| Height (cm) | −37.05 | 7.52 | −36.49 | 7.41 | −36.88 | 7.66 |
| Male | 3.80 | 0.38 | 4.01 | 0.40 | 3.87 | 0.38 |
| Education <12y | 0.48 | 0.24 | 0.53 | 0.27 | 0.49 | 0.25 |
| Married | 0.04 | 0.27 | 0.07 | 0.43 | 0.05 | 0.32 |
| Ever smoked | 1.34 | 0.30 | 1.45 | 0.32 | 1.38 | 0.31 |
| Intercept | 29.50 | 7.40 | 29.50 | 7.40 | 29.50 | 7.50 |
| Interaction | 0.76 | 0.21 | −0.76 | 0.21 | ||
Source: Authors' calculations from US National Health and Nutrition Examination Survey, 1988–1994.
Decomposing Socioeconomic Inequalities in Health
Methods for decomposing the (relative) Concentration Index were laid out by Wagstaff, van Doorslaer, and Watanabe (2003) and described more fully by O'Donnell et al. (2007). McKinnon, Harper, and Moore (2011) also show a similar decomposition for the absolute/generalized index. Wagstaff, van Doorslaer, and Watanabe (2003) first described the decomposition of C, noting that for any health outcome yi one could write a regression function for the average health in the population as
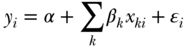
where k represents potential determinants of the outcome (e.g., health behaviors, other socioeconomic factors) and 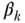 the regression coefficient for each factor. Substituting the determinants of yi in Equation (30) into the equation for the C, one can estimate the contribution of each of several potential determinants via the following equation:
the regression coefficient for each factor. Substituting the determinants of yi in Equation (30) into the equation for the C, one can estimate the contribution of each of several potential determinants via the following equation:
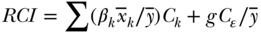
where now 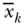 is the mean of xki,
is the mean of xki, 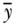 is still the population average health, and Ck is the relative C for determinant k. Equation (31) shows that the overall C can be decomposed into an “explained” part that is due to factors that affect the outcome and are differentially distributed by the socioeconomic ranking variable, and an “unexplained” part. The first component of the explained part
is still the population average health, and Ck is the relative C for determinant k. Equation (31) shows that the overall C can be decomposed into an “explained” part that is due to factors that affect the outcome and are differentially distributed by the socioeconomic ranking variable, and an “unexplained” part. The first component of the explained part 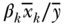 is the determinant's elasticity with respect to the outcome: it measures the percentage change in y for a 1% change in xk. The second component (Ck) is the association between the determinant and the socioeconomic ranking variable, as measured by the relative concentration index.
is the determinant's elasticity with respect to the outcome: it measures the percentage change in y for a 1% change in xk. The second component (Ck) is the association between the determinant and the socioeconomic ranking variable, as measured by the relative concentration index.
As an example, Table 5.6 shows the decomposition of socioeconomic inequalities for physical activity (measured using total metabolic equivalents) using data from the World Health Surveys on men in the Americas region. The overall relative concentration index for total physical activity using an asset-based index of socioeconomic position (Ferguson et al. 2003) was –0.127 (95% CI –0.06, –0.20), indicating that greater total physical activity expenditure is more concentrated among men with fewer assets. Education and urban location make the largest proportional contributions to overall socioeconomic inequality. Table 5.6 also makes clear that important contributors to overall C must be both strong determinants of the outcome and associated with the measure of socioeconomic position.
TABLE 5.6 DETERMINANTS OF SOCIOECONOMIC INEQUALITY IN PHYSICAL ACTIVITY AMONG MEN IN THE AMERICAS REGION
| Elasticity | Relative Conc | Contribution | Percentage | |
| (βkxk/y) | Index (Ck) | to C | contribution | |
| Age | −0.86 | 0.03 | −0.026 | 20.1 |
| BMI | −0.49 | 0.02 | −0.012 | 9.5 |
| Urban | −0.35 | 0.09 | −0.033 | 26.1 |
| Single | −0.11 | −0.04 | 0.005 | −3.6 |
| Divorced/Widowed | −0.03 | −0.19 | 0.007 | −5.1 |
| Current smoking | 0.01 | −0.15 | −0.001 | 1.1 |
| Low Alcohol | −0.05 | 0.06 | −0.003 | 2.3 |
| Moderate/High Alcohol | −0.01 | −0.09 | 0.001 | −0.4 |
| Low Fruit/Vegetable | −0.03 | −0.07 | 0.002 | −1.5 |
| Self-Rated Health: Good | −0.02 | 0.03 | −0.001 | 0.4 |
| Self-Rated Health: Moderate | 0.03 | −0.06 | −0.002 | 1.3 |
| Self-Rated Health: Bad/Very Bad | −0.02 | −0.15 | 0.003 | −2.5 |
| Education | −0.28 | 0.18 | −0.052 | 40.7 |
| Permanent Income | −0.09 | 0.06 | −0.005 | 4.2 |
| Residual | −0.009 | 7.4 | ||
| Total | −0.127 | 100.0 |
Source: Authors' calculations from the World Health Survey, 2002.
Empirical examples of socioeconomic inequality decomposition are now numerous in the literature (e.g., van Doorslaer and Koolman 2004; Hosseinpoor et al. 2006; Costa-Font and Gil 2008; McKinnon, Harper, and Moore 2011), including decomposition of changes in socioeconomic gradients using a Blinder–Oaxaca-type method (O'Donnell et al. 2007; Maika et al. 2013), and methods for implementing decomposition analysis using common statistical software are also available (O'Donnell et al. 2007; Speybroeck et al. 2010).
Conclusions
Measuring health inequality involves a number of ethical, conceptual, and pragmatic issues. Even for simple pairwise comparisons, issues such as the scale of measurement can lead to qualitatively different results depending on the measure chosen. Analysts have a large number of possible choices, and we would argue that it makes sense for analysts to first focus on which aspects of inequality they deem most relevant for the question at hand and to provide sound arguments for their choices. Clearly the literature on health inequality measurement is thriving and we hope to see additional research into new measures of health inequality. However, given the inherent value judgments involved (Harper et al. 2010) it seems unlikely that any single measure of inequality will be able to capture all of the dimensions of a concept so fraught with philosophical and ethical ambiguity (Temkin, 1993).
References
- An, R. (2015) Educational disparity in obesity among U.S. adults, 1984–2013. Annals of Epidemiology, 25 (9), 637–642.e5.
- Asada, Y. (2007) Health Inequality: Morality and Measurement, University of Toronto Press, Toronto.
- Asada, Y. and Hedemann, T. (2002) A problem with the individual approach in the WHO health inequality measurement. International Journal for Equity in Health, 1 (1), 1.
- Atkinson, A.B. and Brandolini, A. (2010) On analyzing the world distribution of income. World Bank Economic Review, 24 (1), 1–37.
- Belizán, J.M., Cafferata, M.L., Belizán, M., and Althabe, F. (2007) Health inequality in Latin America. Lancet, 370 (9599), 1599–1600.
- Benichou, J. (2001) A review of adjusted estimators of attributable risk. Statistical Methods in Medical Research, 10, 195–216.
- Blackorby, C., Donaldson, D., and Auersperg, M. (1981) A new procedure for the measurement of inequality within and among population subgroups. Canadian Journal of Economics, 14 (4), 665–685.
- Blinder, A.S. (1973) Wage discrimination: reduced form and structural estimates. Journal of Human Resources, 436–455.
- Borrell, L.N. and Talih, M. (2011) A symmetrized Theil index measure of health disparities: an example using dental caries in U.S. children and adolescents. Statistics in Medicine, 30 (3), 277–290.
- Bourguignon, F., Levin, V., and Rosenblatt, D. (2004) Declining international inequality and economic divergence: reviewing the evidence through different lenses. Economie Internationale, 100, 13–25.
- Braveman, P., Krieger, N., and Lynch, J. (2000) Health inequalities and social inequalities in health. Bulletin of the World Health Organization, 78 (2), 232–234.
- Braveman, P., Starfield, B., Geiger, H.J., and Murray, C.J.L. (2001) World Health Report 2000: how it removes equity from the agenda for public health monitoring and policy commentary: comprehensive approaches are needed for full understanding. British Medical Journal, 323 (7314), 678–681.
- Chakravarty, S.R. (2001) The variance as a subgroup decomposable measure of inequality. Social Indicators Research, 53 (1), 79–95.
- Charafeddine, R., Demarest, S., Van der Heyden, J., et al. (2013) Using multiple measures of inequalities to study the time trends in social inequalities in smoking. European Journal of Public Health, 23 (4), 546–551.
- Chen, Z. and Roy, K. (2009) Calculating concentration index with repetitive values of indicators of economic welfare. Journal of Health Economics, 28(1), 169–175.
- Costa-Font, J. and Gil, J. (2008). What lies behind socio-economic inequalities in obesity in Spain? A decomposition approach. Food Policy, 33 (1), 61–73.
- Cowell, F.A. (2011) Measuring Inequality, 3rd edn, LSE Perspectives in Economic Analysis, Oxford University Press, Oxford.
- Dalton, H. (1920) The measurement of the inequality of incomes. The Economic Journal, 30 (119), 348–361.
- Darrow, L.A. and Steenland, N.K. (2011) Confounding and bias in the attributable fraction. Epidemiology, 22 (1), 53–58.
- Davey Smith, G. (2011) Epidemiology, epigenetics and the “gloomy prospect”: embracing randomness in population health research and practice. International Journal of Epidemiology, 40 (3), 537–562.
- de Walque, D. and Filmer, D. (2013) Trends and socioeconomic gradients in adult mortality around the developing world. Population and Development Review, 39 (1), 1–29.
- Edwards, R.D. and Tuljapurkar, S. (2005) Inequality in life spans and a new perspective on mortality convergence across industrialized countries. Population and Development Review, 31 (4), 645–674.
- Erreygers, G. (2009a) Can a single indicator measure both attainment and shortfall inequality? Journal of Health Economics, 28 (4), 885–893.
- Erreygers, G. (2009b) Correcting the concentration index. Journal of Health Economics, 28 (2), 504–515.
- Erreygers, G. (2009c) Correcting the concentration index: a reply to Wagstaff. Journal of Health Economics, 28 (2), 521–524.
- Erreygers, G. (2013) A dual Atkinson measure of socioeconomic inequality of health. Health Economics, 22 (4), 466–479.
- Erreygers, G., Clarke, P., and Van Ourti, T. (2012) “Mirror, mirror, on the wall, who in this land is fairest of all?”—distributional sensitivity in the measurement of socioeconomic inequality of health. Journal of Health Economics, 31 (1), 257–270.
- Erreygers, G. and Van Ourti, T. (2011a) Measuring socioeconomic inequality in health, health care and health financing by means of rank-dependent indices: a recipe for good practice. Journal of Health Economics, 30, 685–694.
- Erreygers, G. and Van Ourti, T. (2011b) Putting the cart before the horse. A comment on Wagstaff on inequality measurement in the presence of binary variables. Health Economics, 20 (10), 1161–1165.
- Ezzati, M., Friedman, A.B., Kulkarni, S.C., and Murray, C.J.L. (2008) The reversal of fortunes: trends in county mortality and cross-county mortality disparities in the United States. PLoS Medical, 5 (4), e66.
- Fairlie, R.W. (2005) An extension of the Blinder–Oaxaca decomposition technique to logit and probit models. Journal of Economic and Social Measurement, 30 (4), 305–316.
- Ferguson, B.D., Tandon, A., Gakidou, E., et al. (2003) Health systems performance assessment: debates, methods and empiricism, in Estimating Permanent Income Using Indicator Variables, World Health Organization, Geneva, pp. 747–760.
- Firebaugh, G. (2003) The New Geography of Global Income Inequality, Harvard University Press, Cambridge, MA.
- Flegal, K.M. (2014) Bias in calculation of attributable fractions using relative risks from nonsmokers only. Epidemiology, 25 (6), 913–916.
- Fortin, N., Lemieux, T., and Firpo, S. (2011) Decomposition Methods in Economics, vol. 4A of Handbook of Labor Economics, Elsevier, San Diego and Amsterdam, pp. 1–102.
- Gakidou, E.E., Murray, C.J., and Frenk, J. (2000) Defining and measuring health inequality: an approach based on the distribution of health expectancy. Bulletin of the World Health Organization, 78 (1), 42–54.
- Galea, S., Tracy, M., Hoggatt, K.J., et al. (2011) Estimated deaths attributable to social factors in the United States. American Journal of Public Health, 101 (8), 1456–1465.
- Hao, L. and Naiman, D.Q. (2010) Assessing Inequality. Quantitative Applications in the Social Sciences, Sage, Thousand Oaks, CA.
- Harper, S., King, N., Meersman, S.C., et al. (2010) Implicit value judgements in the measurement of health inequalities. Milbank Quarterly, 88 (1), 4–29.
- Harper, S. and Lynch, J. (2006) Measuring Health Inequalities, 1st edn, Methods in Social Epidemiology, Jossey-Bass, San Francisco, pp. 134–168.
- Harper, S., Lynch, J., Meersman, S.C., et al. (2008) Trends in area–socioeconomic and race–ethnic disparities in breast cancer incidence, stage at diagnosis, screening, mortality, and survival, 1987–2004. Cancer Epidemiology Biomarkers and Prevention, 18 (1), 121–131.
- Hosseinpoor, A. (2013) Handbook on Health Inequality Monitoring—With a Special Focus on Low- and Middle-Income Countries, World Health Organization, Geneva.
- Hosseinpoor, A.R., van Doorslaer, E., Speybroeck, N., et al. (2006) Decomposing socioeconomic inequality in infant mortality in Iran. International Journal of Epidemiology, 35 (5), 1211–1219.
- Hosseinpoor, A.R., Harper, S., Lee, J.H., et al. (2012) International shortfall inequality in life expectancy in women and in men, 1950–2010. Bulletin of the World Health Organization, 90 (8), 588–594.
- Houweling, T.A.J., Kunst, A.E., Huisman, M., and Mackenbach, J.P. (2007) Using relative and absolute measures for monitoring health inequalities: experiences from cross-national analyses on maternal and child health. International Journal on Equity Health, 6 (1), 15.
- Houweling, T.A.J., Kunst, A.E., and Mackenbach, J.P. (2001) World Health Report 2000: inequality index and socioeconomic inequalities in mortality. Lancet, 357 (9269), 1671–1672.
- Illsley, R., Le Grand, J., and Williams, A. (1986) The Measurement of Inequality in Health, London: Macmillan Press, London, pp. 12–36.
- Jann, B. (2008) The Blinder–Oaxaca decomposition for linear regression models. The Stata Journal, 8 (4), 453–479.
- Jenkins, S.P. (1995) Accounting for inequality trends: decomposition analyses for the UK, 1971–86. Economica, 62 (245), 29–63.
- Jones, F.L. and Kelley, J. (1984) Decomposing differences between groups—a cautionary note on measuring discrimination. Sociological Methods and Research, 12 (3), 323–343.
- Kakwani, N., Wagstaff, A., and van Doorslaer, E. (1997) Socioeconomic inequalities in health: measurement, computation, and statistical inference. Journal of Econometrics, 77 (1), 87–103.
- Keppel, K., Pamuk, E., Lynch, J., et al. (2005) Methodological issues in measuring health disparities. Vital Health Statistics, 2 (121), 1–16.
- Keppel, K.G., Pearcy, J.N., and Klein, R.J. (2004) Measuring Progress in Healthy People 2010. Technical Report 25, National Center for Health Statistics.
- King, N.B., Harper, S., and Young, M.E. (2012) Use of relative and absolute effect measures in reporting health inequalities: structured review. British Medical Journal, 345, e5774.
- Kitagawa, E.M. (1955) Components of a difference between two rates. Journal of the American Statistical Association, 50 (272), 1168–1194.
- Kjellsson, G., Gerdtham, U.-G., and Petrie, D. (2015) Lies, damned lies, and health inequality measurements: understanding the value judgments. Epidemiology, 26 (5), 673–680.
- Kolm, S.C. (1976) Unequal inequalities: 1. Journal of Economic Theory, 12 (3), 416–442.
- Koolman, X. and van Doorslaer, E. (2004) On the interpretation of a concentration index of inequality. Health Economics, 13 (7), 649–656.
- Kunst, A.E. and Mackenbach, J.P. (1995) Measuring Socioeconomic Inequalities in Health, World Health Organization, Regional Office for Europe, Copenhagen.
- Le Grand, J. (1987) Inequalities in health: some international comparisons. European Economic Review, 31 (1–2), 182–191.
- Leibler, J.H., Zwack, L.M., and Levy, J.I. (2009) Agreement with inequality axioms and perceptions of inequality among environmental justice and risk assessment professionals. Health, Risk and Society, 11 (1), 55–69.
- Levine, B.J. (2007) What does the population attributable fraction mean? Prevalent Chronic Diseases, 4 (1), 1–5.
- Levy, J.I., Chemerynski, S.M., and Tuchmann, J.L. (2006) Incorporating concepts of inequality and inequity into health benefits analysis. International Journal for Equity in Health, 5, 2.
- Machado, J.A. and Mata, J. (2005) Counterfactual decomposition of changes in wage distributions using quantile regression. Journal of Applied Econometrics, 20, 445–465.
- Maguire, K. and Sheriff, G. (2011) Comparing distributions of environmental outcomes for regulatory environmental justice analysis. International Journal of Environmental Research and Public Health, 8 (5), 1707–1726.
- Maika, A., Mittinty, M., Brinkman, S., et al. (2013) Changes in socioeconomic inequality in Indonesian children's cognitive function from 2000 to 2007: a decomposition analysis. PLoS ONE, 8 (10), e78809.
- McKinnon, B., Harper, S., and Moore, S. (2011) Decomposing income-related inequality in cervical screening in 67 countries. International Journal of Public Health, 56 (2), 139–152.
- Miettinen, O.S. (1974) Proportion of disease caused or prevented by a given exposure, trait or intervention. American Journal of Epidemiology, 99, 325–332.
- Mookherjee, D. and Shorrocks, A. (1982) A decomposition analysis of the trend in UK income inequality. The Economic Journal, 92 (368), 886–902.
- Moreno-Betancur, M., Latouche, A., Menvielle, G., et al. (2015) Relative index of inequality and slope index of inequality: a structured regression framework for estimation. Epidemiology, 26, 518–527.
- Moser, K., Frost, C., and Leon, D.A. (2007) Comparing health inequalities across time and place–rate ratios and rate differences lead to different conclusions: analysis of cross-sectional data from 22 countries 1991–2001. International Journal of Epidemiology, 36 (6), 1285–1291.
- Murray, C.J.L., Gakidou, E.E., and Frenk, J. (1999) Health inequalities and social group differences: what should we measure? Bulletin of the World Health Organization, 77 (7), 537–543.
- National Cancer Institute (2013) Health disparities calculator (hd*calc), version 1.2.4, October 2013.
- Nau, C. and Firebaugh, G. (2012) A new method for determining why length of life is more unequal in some populations than in others. Demography, 49, 1207–1230.
- Navarro, V. (2000) Assessment of the World Health Report 2000. Lancet, 356 (9241), 1598–1601.
- Oaxaca, R. (1973) Male–female wage differentials in urban labor markets. International Economic Review, 14 (3), 693–709.
- O'Donnell, O., van Doorslaer, E., Wagstaff, A., and Lindelow, M. (2007) Analyzing Health Equity Using Household Survey Data: A Guide to Techniques and Their Implementation, World Bank, Washington, DC.
- Pamuk, E.R. (1985) Social class inequality in mortality from 1921 to 1972 in England and Wales. Population Studies, 39 (1), 17–31.
- Parker, S.C. (1999) The inequality of employment and self-employment incomes: a decomposition analysis for the U.K. Review of Income and Wealth, 45 (2), 263–274.
- Pearcy, J.N. and Keppel, K.G. (2002) A summary measure of health disparity. Public Health Reports, 117 (3), 273–280.
- Pigou, A.C. (1912) Wealth and Welfare, Macmillan, London.
- Pollak, R.A. (1971) Additive utility functions and linear Engel curves. The Review of Economic Studies, 38 (4), 401–414.
- Powers, D.A. and Yun, M.-S. (2009) Multivariate decomposition for hazard rate models. Sociological Methodology, 39, 233–263.
- Preston, S.H., Haines, M.R., Pamuk, E., and International Union for the Scientific Study of Populations (1981) Effects of Industrialization and Urbanization on Mortality in Developed Countries, Ordina Editions, Liege, Belgium, pp.233–254.
- Ramsay, S.E., Morris, R.W., Lennon, L.T., et al. (2008) Are social inequalities in mortality in Britain narrowing? Time trends from 1978 to 2005 in a population-based study of older men. Journal of Epidemiology and Community Health, 62 (1), 75–80.
- Regidor, E., Sânchez, E., de La Fuente, L., et al. (2009) Major reduction in AIDS-mortality inequalities after HAART: the importance of absolute differences in evaluating interventions. Social Science and Medicine, 68 (3), 419–426.
- Rockhill, B., Newman, B., and Weinberg, C. (1998) Use and misuse of population attributable fractions. American Journal of Public Health, 88 (1), 15–19.
- Scanlan, J. (2000) Race and mortality. Society, 37 (2), 29–35.
- Sen, A. (1992) Inequality Reexamined, Harvard University Press, Cambridge, MA.
- Sen, A. (2002) Why health equity? Health Economics, 11 (8), 659–666.
- Sen, A.K. and Foster, J.E. (1997) On Economic Inequality, 2nd edn, Clarendon Press, Oxford.
- Shorrocks, A.F. and Foster, J.E. (1987) Transfer sensitive inequality measures. The Review of Economic Studies, 54 (3), 485–497.
- Smits, J. and Monden, C. (2009) Length of life inequality around the globe. Social Science and Medicine, 68 (6), 1114–1123.
- Speybroeck, N., Konings, P., Lynch, J., et al. (2010) Decomposing socioeconomic health inequalities. International Journal of Public Health, 55 (4), 347–351.
- Talih, M. (2013) A reference-invariant health disparity index based on Renyi divergence. The Annals of Applied Statistics, 7 (2), 1217–1243.
- Talih, M. (2015) Examining socioeconomic health disparities using a rank-dependent Rényi index. The Annals of Applied Statistics, 9 (2), 992–1023.
- Temkin, L.S. (1993) Inequality, Oxford University Press, New York.
- Theil, H. (1967) Economics and Information Theory, North-Holland, Amsterdam.
- van Doorslaer, E. and Koolman, X., (2004) Explaining the differences in income-related health inequalities across European countries. Health Economics, 13 (7), 609–628.
- Wagstaff, A. (2002) Inequality aversion, health inequalities and health achievement. Journal of Health Economics, 21 (4), 627–641.
- Wagstaff, A. (2005) The bounds of the concentration index when the variable of interest is binary, with an application to immunization inequality. Health Economics, 14, 429–432.
- Wagstaff, A. (2009) Correcting the concentration index: a comment. Journal of Health Economics, 28 (2), 516–520.
- Wagstaff, A. (2011) Reply to Guido Erreygers and Tom Van Ourti's comment on “the concentration index of a binary outcome revisited.” Health Economics, 20, 1166–1168.
- Wagstaff, A. and van Doorslaer, E. (2004) Overall versus socioeconomic health inequality: a measurement framework and two empirical illustrations. Health Economics, 13, 297–301.
- Wagstaff, A., van Doorslaer, E., and Watanabe, N. (2003). On decomposing the causes of health sector inequalities with an application to malnutrition inequalities in Vietnam. Journal of Econometrics, 112(1), 207–223.
- WHO Commission on Social Determinants of Health (2008) Closing the Gap in a Generation: Health Equity Through Action on the Social Determinants of Health. Final report of the Commission on the Social Determinants of Health, World Health Organization, Geneva.
- Zhang, Q. and Wang, Y. (2004) Trends in the association between obesity and socioeconomic status in US adults: 1971 to 2000. Obesity Research, 12 (10), 1622–1632.
- Zhang, Q. and Wang, Y. (2007) Using concentration index to study changes in socio-economic inequality of overweight among US adolescents between 1971 and 2002. International Journal of Epidemiology, 36, 916–925.
Appendix
Common Inequality Measures Based on Disproportionality Functions
Table 5A.1 summarizes the measures of inequality derived using basic disproportionality functions (Firebaugh 2003). The basic equation for expressing inequality via disproportionality is 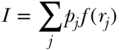 , disproportionality where j indexes social groups, pj is the proportion of the total population in group j, rj is the ratio of health in group j to the population average health, and
, disproportionality where j indexes social groups, pj is the proportion of the total population in group j, rj is the ratio of health in group j to the population average health, and 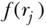 is the disproportionality function.
is the disproportionality function.
TABLE 5A.1 COMMON INEQUALITY MEASURES BASED ON DISPROPORTIONALITY FUNCTIONS
| Inequality measure | Disproportionality function f(rj) | Notes |
| Gini (G) | 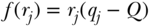 |
j indexes social groups; where qj is the proportion of the total population in |
| groups less healthy than group j, and Qj is the proportion of the total population in groups healthier than | ||
group j (i.e., 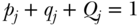 ). ). |
||
| Relative Concentration Index (C) | 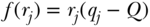 |
j indexes social groups; where qj is the proportion of the total population in |
| groups less advantaged than group j, | ||
| and Qj is the proportion of the total population in groups more | ||
advantaged than group j (i.e., 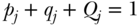 ). ). |
||
| Squared coefficient of variation CV2 | 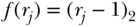 |
j indexes social groups; indicates disproportionality function; squared coefficient of variation interpretation. |
| Theil index (T) | 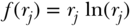 |
j indexes social groups; ln is the natural logarithm. |
| Mean logarithmic deviation (MLD) | 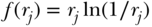 |
j indexes social groups; ln is the natural logarithm. |
| Variance of logs (VarLog) | 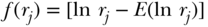 |
j indexes social groups; ln is the natural logarithm; E is expected value. |