CHAPTER SEVENTEEN
A ROADMAP FOR ESTIMATING AND INTERPRETING POPULATION INTERVENTION PARAMETERS

Jennifer Ahern and Alan E. Hubbard

Standardization is one of the earliest epidemiologic tools, used to facilitate comparison of risks or rates of disease across populations with different distributions of confounding variables, such as age and gender (Breslow and Day 1987; Rothman and Greenland 1998). With the advent of multivariable regression approaches and improvements in computing capacity, standardization was relegated to the realm of “descriptive epidemiology.” Multivariable regression certainly has many strengths, such as facilitating simultaneous adjustment for a larger set of confounders including continuous variables through the imposition of parametric assumptions. It is now so well accepted in epidemiology as well as other quantitative fields that researchers need to provide only a brief mention of the regression form in a peer-reviewed publication and the tool is understood and accepted by reviewers from a wide array of disciplines.

Social epidemiology has embraced the regression approach along with other quantitative fields. Although some alternative analysis approaches have been applied to questions about social determinants of health in recent years (Ahern et al. 2013a; Glymour et al. 2008; Nandi et al. 2012; Osypuk et al. 2012), there have been few discussions of the lack of interpretability of the parameter estimated in regression models as a motivation for alternative methods (Ahern, Hubbard, and Galea 2009; Petersen and van der Laan 2014). Regression models estimate association parameters, such as odds ratios, that are dictated by the form of the model, and the parameters may or may not match the scientific question of interest (Ahern, Hubbard, and Galea 2009; Poole 2010). For example, a researcher who is examining the relation of stressful life events with depression, or fresh vegetable availability with obesity, will almost inevitably turn to logistic regression so that she/he can adjust for confounders in quantifying the relation between the exposure and binary outcome of interest. After fitting the adjusted logistic regression, the researcher will have estimated an odds ratio for the relation between exposure and outcome, conditional on the set of confounders. This conditional odds ratio—an estimate of the odds of the outcome in the exposed relative to the odds of the outcome in the unexposed conditional on covariates—is challenging to interpret unless the outcome is rare or the study design guarantees that the odds ratio approximates a more interpretable measure (Kaufman 2010; Poole 2010).

The widespread use of regression models has led not only to estimation of parameters that are challenging to interpret but also to neglect of the most basic question behind any scientific endeavor: what causal effect is of interest? This neglect is certainly not unique to the study of social determinants of health, but the complexity of many questions about social determinants means it is an issue that social epidemiology would benefit from considering more carefully. For example, in research on neighborhood characteristics and health there have been endless documentations of associations, without much careful consideration of the array of different “experiments” that might be of interest (Oakes 2004). Changes in a neighborhood while the individual remains in place imply one experiment, while changes in the neighborhood due to moves from one neighborhood to another indicate a distinct experiment. Once the question is stated clearly, consideration of the data that would support estimation of such an effect can begin. Similarly, research focused on differences in health between groups defined by characteristics such as race/ethnicity or gender often employ regression analyses and include interaction terms between the characteristic and another variable of interest. The interaction approach does not clearly indicate whether both the characteristic and the other variable are being considered to be intervention variables or whether the characteristic is being included to define strata within which the exposure effect varies (VanderWeele 2009a). Careful statement of the causal effect of interest positions researchers to direct efforts toward answering the question posed, rather than employing analyses that do not answer a specific question.

Fortunately, in recent years epidemiology has embraced the use of formal causal frameworks that require a clear statement of the question of interest, and provide a rigorous approach to assess assumptions and interpret results (Glass et al. 2013; Hernán 2004; Maldonado and Greenland 2002; Pearl 2010a; Petersen and van der Laan 2014; Rothman, Greenland, and Lash 2008; van der Laan and Rose 2011). In parallel, a set of estimators has been developed that free researchers to estimate a wide array of parameters and, importantly, to match the parameter estimated to the question of interest. Many of these estimators are analogous to standardization in that they use prediction or weighting to estimate the outcome under different exposure conditions for a population with a confounder distribution of interest (Ahern, Hubbard, and Galea 2009; Sato and Matsuyama 2003). Because these estimators allow flexible manipulation of the exposure conditions, they can be used to estimate population intervention parameters. In the study of social determinants of health, these population intervention parameters have been used to answer questions about potential changes in the distributions of exposures such as social participation and alcohol outlet density that might be the target of intervention (Ahern et al. 2013b; Leslie et al. 2013). However, limited applications to date suggest the need for broader dissemination of this approach, together with the details of implementation. In this chapter we introduce an approach to the definition and estimation of population intervention parameters, including the steps required for implementation and statistical code, within a framework known as the “causal roadmap” (Petersen and van der Laan 2014; van der Laan and Rose 2011).

Roadmap

The “causal roadmap” provides a framework for defining and interpreting different types of parameters of interest and the methods used for estimation and inference (van der Laan and Rose 2011). In social epidemiology, this type of framework can be critical to keep the question of interest clear, link the question to the actual data available, and provide guidance on the strength of interpretation of the results. This is an eight-step program for statistical analysis that can serve as a common framework for all problems involving estimation from data. It consists of the following steps:

1. State the scientific question and hypothetical experiment.
2. Define the causal model and parameter of interest.
3. Define the sampling process that generated the data.
4. Define the statistical model.
5. Assess identifiability: link the parameter estimable from the observed data to the causal effect.
6. Choose the estimator.
7. Derive an estimate of the sampling distribution (statistical uncertainty).
8. Make inferences (interpret findings).

We develop a social epidemiology example in which we examine the effect of a specific early childhood adversity, physical abuse, on psychopathology in adulthood, through each of these eight steps below.

Scientific Question and Hypothetical Experiment

What Is the “Experiment” That Would Answer the Question?

A helpful way to be clear about the scientific question is to explicitly state the “experiment” that would unambiguously estimate the causal effect of interest. There is a substantial literature now that presents varying viewpoints on how literally to take this experiment. On one extreme is the position that if the proposed experiment is not something we can implement in a randomized trial today, then it is not appropriate to estimate (Harper and Strumpf 2012; Hernán and Taubman 2008; Hernán and VanderWeele 2011). On another extreme is the position that any experiment could be an interesting and informative parameter regardless of its plausibility (Petersen, Sinisi, and van der Laan 2006; van der Laan and Rose 2011). In this chapter, we leave these arguments to the side and simply recommend that each researcher read this and other related literature to inform the development of his/her own perspective on what kinds of hypothetical experiments might translate to parameters will usefully move scientific knowledge forward (Galea 2013; Kaufman and Harper 2013).

A common hypothetical experiment of interest is to assign the entire target population to experience the exposure, then assign the same population to experience no exposure, and quantify the difference in the mean outcome between these two exposure conditions. However, this is just one of many experiments that might be of interest. Other hypothetical experiments define parameters that match more closely to changes in exposure we might hope to achieve in the population. For example, usually we would not want to impose a harmful level of exposure on the entire population, so a comparison of the existing exposure distribution to removal of or reduction in a harmful exposure might be more relevant (Greenland and Drescher 1993; Hubbard and van der Laan 2008). The literature is growing on alternative experiments, elaborated in the “Other parameters and future directions” section below.

---

Our example was motivated by the growing literature on early childhood adversity and how these experiences may shape psychopathology over the life course (Kessler, Davis, and Kendler 1997; Kessler et al. 2010; McLaughlin et al. 2012). Specifically, we use an example in which the scientific question is: what is the effect of physical abuse on psychopathology in adulthood? We consider two hypothetical experiments, specifically: (1) what would be the difference in psychopathology if everyone in the population experienced abuse, compared with if no one experienced abuse; and (2) what would be the difference in psychopathology if abuse remained as observed, compared with if no one experienced abuse?

---

Causal Model and Parameter of Interest

Having defined the scientific question and hypothetical experiment(s), the next step is to use a causal framework to formalize the experiment and thereby define the parameter of interest. Causal graphs are one useful tool to express what we know about the causal relations among variables that are relevant to the question under study (Pearl 2009). We illustrate the use of a causal graph, specifically a directed acyclic graph or DAG, to depict the causal relations between variables with a simple example of a binary exposure A, a binary outcome Y, and one categorical confounding variable W. The DAG for these relations is depicted in Figure 17.1. The U_W, U_A, and U_Y are the unmeasured exogenous background characteristics that influence the value of each variable. Alternatively, the same causal relations among variables can be represented with a series of equations:

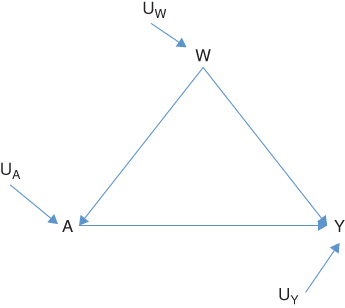
FIGURE 17.1 DIRECTED ACYCLIC GRAPH OR DAG OF THE CAUSAL RELATIONS BETWEEN THE EXPOSURE A, OUTCOME Y, AND CONFOUNDING VARIABLE W

U_W, U_A, and U_Y are the unmeasured exogenous background characteristics.

(1)

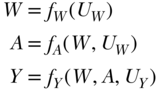
Here f_W, f_A, and f_Y denote that each variable (W, A, and Y, respectively) is a function of its parents and unmeasured background characteristics, but do not impose any particular functional form on these effects. For this reason, they are called non-parametric structural equations. The DAG and this series of non-parametric structural equations represent the same information.

---

Continuing the example, the exposure A is physical abuse, the outcome Y is psychopathology in adulthood, and we use an illustrative scenario in which there is one confounding variable W childhood family socioeconomic status (SES). The DAG in Figure 17.1 and non-parametric structural equations in Equation (1) depict the relations among these variables.

---

Parameter 1: Causal Risk Difference

The first hypothetical experiment we will consider is assigning exposure to the whole population and observing the outcome, and then assigning no exposure to the whole population and observing the outcome. On the non-parametric structural equations, this corresponds to a comparison of the outcome distribution in the population under two interventions: (1) A is set to 1 for all individuals and (2) A is set to 0 for all individuals. These interventions imply two new non-parametric structural equation models, specifically:

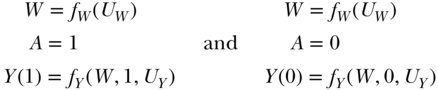
In these equations, A is no longer a function of W because we have intervened on the graph and set A to the values 1 and 0. The new symbols Y(1) and Y(0) indicate the outcome variable in our population if it were generated by the respective non-parametric structural equation models above; these are often called counterfactuals. The difference between the means of the outcome under these two interventions defines a parameter that is often called the “average treatment effect” (ATE) or causal risk difference (CRD):

(2)

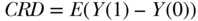
Note that the potential outcomes framework is a common alternative to causal graphs (Rubin 1986). In the potential outcomes framework, a researcher starts with the existence of the counterfactuals of interest, Y(0),Y(1) and then states the assumptions, such as randomization (see section on “identifiability” below), necessary to estimate parameters of the counterfactual distributions from the observed data. The potential outcomes framework does not require the researcher to explicitly postulate the causal model that generated the data. The validity of the randomization assumption cannot be assessed without a causal graph such as a DAG. Thus, a strength of a graphical or structural equation approach is that it ensures that researchers explicitly postulate the causal model and rigorously assess the randomization assumption.

Parameter 2: Causal Population Attributable Risk (CPAR)

The second hypothetical experiment we will consider is leaving exposure as observed in the population and observing the outcome, and then assigning no exposure to the whole population and observing the outcome. On the causal graph, this corresponds to a comparison of the outcome distribution in the population under two scenarios: (1) A remains as observed and (2) A is set to 0 for all individuals. The difference between the means of the outcome under these two interventions defines a simple but useful parameter that we refer to as the causal population attributable risk (Greenland and Drescher 1993); it has also been described as a population intervention model parameter (Hubbard and van der Laan 2008):

(3)

---

For our example, the CRD captures the difference in psychopathology if the entire population experienced physical abuse compared to if no one experienced abuse. The CPAR captures the difference in psychopathology comparing physical abuse as observed in the population to that if no one experienced abuse. This latter parameter quantifies the difference in the risk of psychopathology if we were able to prevent all occurrence of physical abuse.

---

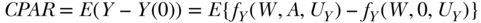
The Sampling Process That Generated the Data

The graphical causal model defines how the joint distribution of the variables of interest are generated in the target population. We can denote the observed data that we draw from the target population as O = (W,A,Y), meaning that the observed data O is comprised of the random variables W, A, and Y. As the next step in the roadmap, we need to specify how the observed data were sampled from the target population. The simplest case is a random sample of individuals; however, many studies are based on what can be conceptualized as biased samples, such as probability sampling or case-control sampling. For biased samples, see Part IV in van der Laan and Rose (2011). Some studies are based on data that are complete enumerations of the target population rather than a sample (e.g., all births in a particular geographic area and time frame). In those situations, variability is no longer a function of sampling; instead it arises from variation in a theoretical experiment involving the mechanisms that generate the exposures and outcomes of interest. However, if the standard error (SE) is derived based on treating the data as a sample from a larger population, the resulting inference is conservative (Balzer, Petersen, and van der Laan 2014; Robins, 1988).

---

For our example, the observed data we drew for the study of physical abuse and its effect on psychopathology in adulthood were a simple random sample of 1000 individuals drawn from the target population (1000 random samples of O = (W,A,Y)).

---

The Statistical Model

In the case of simple random sampling, we can break up the distribution of the observed data as follows: 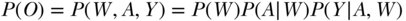. In words, this says that the probability distribution of the observed data (in our example the observed variables W, A, and Y) can be decomposed as a product of conditional distributions, based on their relations in the graphical causal model. Specifically, the graph will imply independence of nodes/variables, conditional on the parents of these nodes. Fortunately, to estimate a parameter of interest, the researcher does not necessarily need to specify these whole distributions and conditional distributions. Each estimator requires certain parts of the distribution; for example, some require estimates of = mean of Y within subgroups (A,W), or the regression of the outcome on the exposure and confounders.

At this stage in the roadmap the researcher specifies what statistical model she/he will use to estimate or other elements of the probability distribution that are needed to estimate the parameter of interest. By “statistical model” here we mean any constraints on the model form that are imposed by knowledge about the process—known aspects of how the data were generated. For our illustration in this chapter, we assume a simple parametric model—one with main effects terms for exposure (A) and covariates (W). However, we note that there are exciting developments in semi-parametric, data-adaptive estimation approaches that reduce bias. We elaborate on semi-parametric approaches at the end of this section.

---

For our example, we use a parametric statistical model. Our analysis includes main effects terms for the exposure of physical abuse (A) and the covariate of family SES (W), and we assume that this specification will correctly capture how these variables relate to psychopathology in adulthood (Y).

---

Assess Identifiability

If the scientific question is about a causal effect, the researcher needs to formally make the link between associations of observed or assigned exposure values and resulting outcomes, and causal effects of a hypothetically assigned set of exposure interventions and corresponding array of outcomes. To make this link the researcher must consider a set of identifiability assumptions, specifically the assumptions necessary to “identify” the association from an observational study as a quantification of the causal effect. If some of the assumptions are significantly violated, this exercise provides an important guide to what is necessary to improve the causal interpretation of future studies.

Temporality

First, we assume that the confounders came before the exposure and the exposure came before the outcome. This is known as the temporal ordering assumption; temporality has long been a commonly agreed upon requirement for causality. This assumption is the same as the temporal ordering suggested in the causal graph. Sometimes temporal ordering is established by the structure of the data. At other times, it must be asserted by the researcher, who proposes a causal graph with an implied temporal ordering based on the most plausible causal sequence. For example, certain confounders may be fixed or tend to be static over long time periods (e.g., gender, marital status, education) and it might be reasonable to assume they came before the exposure even if covariates and exposure were measured at the same time.

---

Temporality: For our example, temporality requires that the confounding variable childhood family SES (W) comes before physical abuse (A), and that both W and A come before psychopathology in adulthood (Y). Structurally, the W and A from childhood temporally precede the outcome Y in adulthood. The details of how W and A are assessed would determine how they are temporally sequenced; for example, if W is measured at the birth of the child, this would ensure the required temporal ordering. If W and A were measured in a way that the temporal ordering was unclear, such as retrospective recall of the adult, then the most likely ordering should be considered. Childhood SES may be generally stable, so assuming it comes before the abuse may be reasonable; however, if the reality were that the abuse changed the SES of the family then the temporality would be specified incorrectly. For our example, we will stipulate that the assumption of temporality is met.

---

Randomization

Second, we assume that there are no unmeasured confounders for the exposure–outcome relation being studied. This is known as the randomization assumption because if all confounders have been measured, within strata of the confounders the exposure is effectively randomized. Unmeasured confounders are always a concern in epidemiology, and several authors have raised particular concern about this issue for social exposures (Oakes 2004). For any exposure, even when we measure all confounders based on current knowledge, there still may be unmeasured confounders and mismeasured confounders. The randomization assumption can be assessed from a causal graph, or it might just be asserted without using a graph to justify the assumption. It is worth emphasizing that if the relations among variables in the graph do not represent the true causal structure, the estimated association based on that graph can be biased in unpredictable directions.

---

Randomization: In this simple example, we specified that childhood family SES (W) is the only common cause of A and Y. Thus the causal graph implies that A is independent of (Y(0),Y(1)) within strata of W. An alternative way of conceptualizing this is that within strata of W, A is effectively randomized. However, in all real-world analyses, unmeasured confounders are a substantial concern.

---

Stability

Third, we assume that the effect of the exposure on the outcome for any individual is independent of the exposures and outcomes, or counterfactuals, of other individuals—an assumption known as the stability assumption or stable unit treatment value assumption (Rubin 1990, 1980). This assumption of independence is not met when phenomena such as biological or social contagion mean that study participants may influence the counterfactuals of other participants. When there is a concern about violation of stability there are solutions in the design and analysis phases available. In the design phase, sampling participants that are sufficiently distant from each other in geographic or social space is likely to ensure this independence. If groups (e.g., communities or villages) are the level at which exposure varies, whether observed or assigned, it will be important to consider the potential for stability violation between the groups (VanderWeele 2008). There is currently research on estimating causal associations in general dependent data, so techniques allowing for stability violations will eventually be more generally available (van der Laan 2012).

---

Stability: In our study, the counterfactuals of individuals might not be independent if participants knew one another. For example, say there were a participant who would develop psychopathology in adulthood in response to childhood physical abuse (Y(0) = 0, Y(1) = 1). However, that participant would not develop psychopathology in response to abuse if a close friend also experienced abuse (Y(0) = 0, Y(1) = 0). If that close friend were also a study participant, this scenario would violate the stability assumption. This is because the effect of the exposure on the outcome for the initial participant depends on the exposure of another study participant. Such violations might occur if the population were sampled from a small, close-knit geographic area. For our example, we will posit that the sample was drawn from a large enough area that it is unlikely that there will be interference among the participants.

---

Positivity

Fourth, for the CRD parameter, we assume that all exposures are possible for all members of the study population, an assumption known as the positivity assumption or experimental treatment assignment assumption. For CPAR we only need to assume that all subjects have a positive probability of being unexposed, since we only set exposure to take the unexposed value. Practically, this means that within subgroups defined by combinations of covariates, some individuals have to be observed as exposed and others as unexposed. Unlike some of the other assumptions, positivity can be examined in the data, and researchers can make decisions about how to deal with violations. The propensity score, 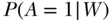, is an extremely useful tool for examining positivity in the data (Ahern et al. 2013a; Petersen et al. 2012). Positivity violations can be classified as structural, in which there are target population subgroups that never or always experience the exposure, or chance, in which there are subgroups of study data that never or always experience the exposure due to sampling variability (Petersen et al. 2012). While the basic implication of a positivity violation, that you cannot estimate the effect of an exposure in a group that only experiences one exposure value, is the same for all positivity violations, decisions about how to deal with the violation may differ based on the type. For example, when there is a structural violation, it may be most reasonable to change the parameter of interest to respect the reality that certain groups never or always experience the exposure by (1) restricting the analysis population to those who do have experimentation in the exposure or (2) defining a dynamic parameter in which the change in the exposure of interest covers the range that is observed given covariates. Otherwise, the researcher will be attempting to examine exposures for subgroups in which they never occur.

---

Positivity: In these simulated data, there is variation in physical abuse (A), within each of the five quintiles of childhood family SES (W) (0 < P(A = 1 | W = w) < 1 for all w = 1, 2, 3, 4, 5). However, for the highest quintile of W the propensity approaches 0 (i.e., those with the highest family SES have a low propensity for physical abuse). Thus, while there are no structural violations of positivity within the data, there could be chance violations depending on the sample size. We did not have any chance violations in our simulated data, so positivity is met, but there are only eight individuals with A = 1 at W = 5, meaning that the estimate for this cell is based on little data.

---

Consistency

Finally, consistency states that the observed outcome for an individual under their observed exposure is one of the counterfactual outcomes that might have been observed for that individual (Y | A = a) = Y(a). This implies that if an individual had been counterfactually assigned A = a instead of experiencing A = a, the outcome would have been the same. In the structural causal model framework this is not considered an assumption, but rather a theorem that derives from the formal definition of counterfactuals (Pearl 2010b). In the potential outcomes framework it is discussed as an assumption because counterfactuals are taken to be primitive quantities that require consistency as an assumption to be defined. In either situation, consistency requires that any assignment of exposure A to a results in the same outcome for a given individual. This may not be met when there are multiple versions of exposure, also called compound exposures, such that assignment to a does not indicate one specific exposure but rather one of several versions of an exposure (see the example below) (Cole and Frangakis 2009; VanderWeele 2009b). In this situation, if the versions result in different outcomes, consistency will be violated. To address this problem, the exposure definition can be refined so that it does not contain versions that result in different outcomes, although it may result in exacerbation of problems with positivity. Alternatively, if a researcher proceeds with an exposure classification that may contain multiple versions of the exposure, the estimated association is for A being set to a random draw from the variation present within the classification of A = a (van der Laan et al. 2005).

---

Consistency: For our example, the assumption of consistency is likely to be reasonable because the exposure is one specific kind of event: physical abuse. In contrast, if the exposure were any of an array of events that might be qualitatively quite different (e.g., parental divorce or abuse), then these versions of exposure would result in different counterfactual outcomes and consistency would not be met. For our example, we will posit that the physical abuse was sufficiently clearly defined in terms of the nature and timing of the experience to meet consistency.

---

Link the Causal Effect to the Association in the Observed Data

Now we can put together the above assumptions to represent a tractable problem of directly estimating a causal effect, or distributions of counterfactuals, as a parameter of the observed data. This is done in the following set of equalities:

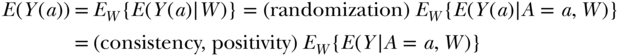
The left-hand side of the equation is a function of the counterfactuals E(Y(a)) and the right-hand side of the equation is a function of the observed data, specifically E(Y|A,W) and the distribution of W(E_W). One can do this equivalently for a = 0 and a = 1, to derive the parameters of interest:

(4)

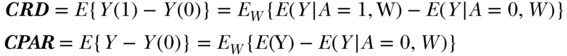
This identifiability exercise is how we take the parameter of a counterfactual experiment of interest and elaborate and assess the assumptions necessary to estimate the causal parameter from the observed data. In the next section, we elaborate one approach to estimate the CRD and CPAR.

Choose an Estimator

An estimator is an algorithm that when applied to the data generates an estimate of the parameter of interest. There are several estimators that can estimate the CRD and CPAR. There are those that are based on substitution estimators, estimating equation approaches, and matching. We present only a parametric substitution estimator for this introduction to the roadmap. Propensity score matching and estimating equation approaches are alternative estimators, described in Rosenbaum and Rubin (1983) and van der Laan and Robins (2002). Semi-parametric estimators are discussed at the end of this section. In online Appendix A (available at https://ahubb40.github.io/Roadmap/appendix), code (in R and Stata) is provided for the implementation of the example analysis of simulated data elaborated below.

Substitution Estimators

Substitution estimators are based on plugging in estimates of functions of the observed data into Equation (4). The form of the estimator for the CRD is

(5)

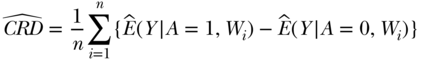
where the ^ or “hat” notation indicates an estimate of the corresponding parameter. In the case of Equation (5), the 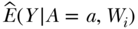represents a prediction of the mean of Y given A = a and W is the ith person's covariate value, where this prediction might be based on a regression fit of Y on A,W. This general substitution estimator has been called g-computation (Robins 1986).

The implementation of a parametric substitution estimator can be broken down into simple steps.

1. First, we implement a regression of the outcome Y on exposure A and covariates W. This provides an estimate of .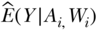

---

In our example we are interested in the effect of physical abuse on psychopathology. For this first step, we use a logistic regression because the outcome is binary. With a main effect term for the exposure and indicator variables for the categories of family SES, the resulting model is

Note, for a binary outcome, E(Y|A,W) = Pr(Y = 1|A,W), so that the conditional mean and probability of the outcome are interchangeable.

---

2. Next, we use the regression model from the first step to predict values of the outcome for each individual in the dataset while we manipulate the exposure A to take values that define our parameter of interest. For the CRD, this means manipulating A to take the value of 1 and predicting outcomes, then manipulating A to take the value of 0 and predicting outcomes. This provides us with estimates of 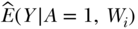and 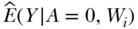that are key pieces that we need to estimate the parameter of interest (see Equation (5)).

---

Continuing our example, for each individual in the dataset we estimate the predicted probability of psychopathology if the person had experienced physical abuse (A = 1) and if the person had not experienced abuse (A = 0). Each individual will have experienced one but not both of these exposure conditions, so we rely on the model estimated in step 1 to predict outcomes under exposures that were not observed for some individuals:

An example set of results from this prediction of psychopathology can be found in Table 17.1. Each individual has a predicted probability of psychopathology under exposure and no exposure, and it is consistently higher in the column than the column, reflecting the large positive coefficient on A in the logistic model above. The values of and also depend on the other covariates in the model, in this case the one W. For instance, the individual with ID = 4 has a lower overall psychopathology risk due to being in a higher SES group (SES category 4) that had a negative coefficient in the model above, and the individual with ID = 1 had the highest overall psychopathology risk due to being in the second SES group (SES category 2) that had a positive coefficient in the model above. These individual predicted values cannot be interpreted as estimates of individual counterfactuals, but they illustrate how the exposure and covariates together shape the risk of psychopathology and are an important step in the process of estimating the population-level CRD.

TABLE 17.1 ILLUSTRATION OF PARAMETRIC SUBSTITUTION ESTIMATOR IMPLEMENTATION FOR THE CRD AND CPAR OF THE RELATION BETWEEN PHYSICAL ABUSE AND PSYCHOPATHOLOGY^a

ID	Y	A	W	Ê(Y|A = 1,W)b	Ê(Y|A = 0,W)c	Ê(Y|A,W)d	Ê(Y|A = 1, W) – Ê(Y|A = 0,W)	Ê(Y|A, W) – Ê(Y|A = 0,W)
1	1	1	2	0.277	0.103	0.277	0.173	0.173
2	0	1	3	0.214	0.076	0.076	0.138	0.000
3	0	0	1	0.269	0.100	0.100	0.169	0.000
4	0	0	4	0.196	0.068	0.068	0.128	0.000
…
1000	0	0	5	0.188	0.065	0.065	0.123	0.000
				ÊW[Ê(Y|A = 1, W)]	ÊW[Ê(Y|A = 0, W)]	ÊW[Ê(Y|A, W)]	CRD = ÊW[Ê(Y|A = 1, W) – Ê(Y|A = 0,W)]	CPAR = ÊW[Ê(Y|A, W) – Ê(Y|A = 0,W)]
Mean				0.228	0.082	0.096	0.146	0.014

^a Estimates based on the model: .

^b

^c

^d

---

3. After outcomes have been estimated for each individual under the two exposure conditions of interest, A = 1 and A = 0, the predicted outcomes and the difference between the predicted outcomes are simply averaged across the total population. By averaging across the study population, we get an estimate of the CRD that is standardized to the empirical distribution of the confounders, W (i.e., weight 1/n for each observation). This is an average of the differences between the predicted outcomes of each subject if their A was 1 versus 0, allowing W to remain as observed and make its own contribution to the outcome. This third step provides an estimate of the CRD in Equation (5).

---

From our example, we take the mean of predicted psychopathology if all individuals experienced physical abuse, the mean if all experienced no abuse, and the mean of the differences: mean(P(psychopathology|A = 1,W) – p(psychopathology|A = 0,W)). Based on our analysis, the risk of psychopathology if the whole population experienced physical abuse is 0.228 and if the whole population experienced no abuse the risk is 0.082. The difference between these (or, equivalently, the mean of individual differences) provides us with an estimate of the CRD, in this case 0.146. In Table 17.1, these are the values in the bottom row where the mean has been calculated across all 1000 individual predicted values. We can see from this table how the population-level estimated risks are an average across the individual predicted outcomes that reflect both exposure conditions and covariates, thereby estimating the outcome under different exposure conditions, standardized to the covariate or W distribution of the total population.

---

Estimation of the CPAR follows the same sequence of steps, with the difference that exposure as observed is compared to exposure set to 0. The form of the estimator for the CPAR is

(6)

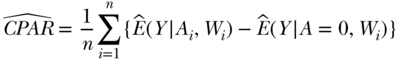
where 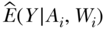is the predicted Y for each individual given their observed exposure, and covariates and 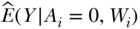are estimated as above. The difference between the outcome estimated under A_i and the outcome estimated under A = 0 is averaged across the study population as above, providing an estimate of the CPAR.

---

From our example analysis, we compare the mean psychopathology with abuse as observed to a situation in which no abuse is experienced: mean(P(psychopathology|A,W) – p(psychopathology|A = 0,W)) and this provides us with an estimate of the CPAR: 0.014. This captures a difference between the risk of psychopathology for abuse as experienced 0.096 and the risk of psychopathology if all abuse were removed 0.082. In Table 17.1, column , we can see that only observations such as the individual with ID = 1, who did experience physical abuse, contribute to this measure that captures the difference in risk associated with removal of abuse. Those who did not experience abuse (e.g., those with ID = 2–4) do not have an altered risk of the outcome as a result of this intervention because their exposures have not been changed. Thus they contribute a 0 to the column. The overall parameter is an average across those who are and are not affected by the change in exposure, so it is a measure of association that reflects both the strength of the association between abuse and psychopathology, as well as the distribution of abuse in the population. Because abuse was only experienced by 8.9% of the study population, the magnitude of the CPAR is much smaller than the CRD.

---

Derive an Estimate of the Sampling Distribution

To derive an estimate of the sampling distribution for a parametric substitution estimator, a bootstrap approach is necessary. To bootstrap, the data are sampled with replacement a sufficient number of times, typically B = 1000. The estimator is repeated in each sample and the SE estimated as simply the sample standard deviation of the parameter estimates across the B samples. For more complex designs, the re-sampling should mimic the original design, incorporating sampling of strata, clusters, and individual units in stages, as structured originally. The estimate of the parameter from each bootstrap sample, say CRD_b for b = 1,2,…, B, is stored, and the standard error calculation is simple:

---

Based on the bootstrap, for our example the 95% confidence interval for the CRD of 0.146 is 0.057 to 0.235. The 95% confidence interval for the CPAR of 0.014 is 0.005 to 0.023. In both instances, the confidence intervals exclude the null value of 0.

---

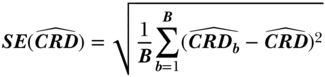
Interpret Your Findings

The final step in the roadmap is making inference or interpretation of findings. Whether and to what degree the identifiability assumptions have been met for any analysis should inform the causal strength with which the findings are interpreted. Taking the CRD as an example, if there were major concerns about identifiability assumptions (e.g., temporal ordering unclear, key confounder not measured) the parameter could still be interpreted as the association that is captured by the parameter of the observed data 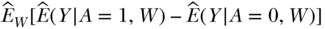. In words, this association is the difference in the outcome associated with everyone exposed compared to everyone unexposed in the total population, accounting for the measured confounders. This could also be discussed as a parameter that is as close as we can get to the causal effect of A on Y given the limitations of the observed data, as long as all caveats about unmet assumptions are carefully detailed. If in the end the identifiability assumptions were met, then the parameter could be interpreted as the effect captured by the causal parameter: Ê[Y(1) – Y(0)]. In words, this is the effect of the exposure on the outcome in the total population.

---

Wrapping up our example, we stipulated that we have met all of the identifiability assumptions and thus we can interpret our estimate of the CRD causally as follows. There would be a 0.146 difference in the risk of psychopathology (or 146 fewer psychopathology cases per 1000) in adulthood if everyone in the population experienced physical abuse compared with if no one experienced abuse. For the CPAR, interpretation is that there would be a 0.014 lower risk of psychopathology (or 14 fewer psychopathology cases per 1000) in adulthood if we could prevent all physical abuse. If we extend our example to the more realistic scenarios in which there might be some concern about unmeasured confounding, or some other assumption that might not be fully met, we instead interpret as follows. The difference in adult psychopathology associated with everyone exposed to physical abuse compared with everyone unexposed to abuse in the total population is 0.146, accounting for childhood SES.

---

Semi-parametric Estimation

For this chapter, we assumed a simple parametric model, which is standard practice in epidemiology. In this case, the simulated data are simple so a simple model can fit the data well. By “parametric” we mean that we assume that we know the form of the relation between the A, W, and Y variables and have correctly specified this form with a set of constants called “parameters.” In the example, we assumed that the regression in the first step for 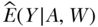with main effects terms for exposure and covariates was correct; alternatively, we might have decided to include selected interaction or non-linear terms. Even if terms that allow interaction or non-linearity are included, this approach assumes a parametric model because it asserts that the form chosen by the researcher is correct.

Given the limitations of computing capacity historically, parametric models were used out of necessity rather than a belief that these models were true. Certainly researchers have done their best to include covariates and exposure in sensible forms based on understanding how variables are related. For example, age might be included in a model with a squared term to account for the possibility of a non-linear relation. While this is reasonable, and likely better than assuming a linear relation, it could be the case that something even more flexible, like a smoothing function such as loess or polynomial spline, would capture the form better. Further, there might be interactions between the exposure and covariates that are not suspected by the researcher and therefore not included in the model. If the model specified by the researcher is not correct, there may be bias in the estimate of the parameter of interest.

Fortunately, with the recent increase in computing capacity, there are new semi-parametric methodologies that free researchers from the need to impose parametric models. In following the roadmap, researchers define the scientific question and parameter(s) of interest, such as the CRD and CPAR in our example, as a primary step in a scientific investigation. One powerful consequence of this approach is that the parameter of interest is not tied to a parametric regression coefficient, and thus a researcher is free to fit nearly any model because there is no need to interpret model coefficients directly. A researcher could choose to use a particular semi-parametric modeling approach, such as loess or polynomial spline, but selecting one particular semi-parametric approach still imposes an arbitrary constraint. Theory says “the more the merrier” with classes of models considered, as long as the best model is selected the right way using cross-validation (van der Laan, Polley, and Hubbard 2007). For example, rather than asserting a model, in the first implementation step Ê(Y|A,W) can be estimated with a data adaptive, machine-learning approach such as SuperLearner (van der Laan, Polley, and Hubbard 2007). This approach can fit models with almost infinite flexibility, since it allows the user to enter a library of potential model selection routines, such as stepwise procedures, polynomial splines (Friedman 1991), and classification and regression trees (Breiman et al. 1984), and uses cross-validation to select the best routine or weighted combination of routines without overfitting (Sinisi et al. 2007). This data-adaptive semi-parametric approach represents a potential improvement over the parametric model. There are other approaches based on a model for exposure, such as inverse probability of treatment weighted (IPTW) estimators (Hernán, Brumback, and Robins 2000; Robins and Rotnitzky 2004) and propensity score-matching estimators (Rosenbaum and Rubin 1983) that can also incorporate a data-adaptive semi-parametric approach to model the exposure. Furthermore, there are methods that gain robustness by estimating both exposure and outcome models, again potentially incorporating a data-adaptive semi-parametric approach (van der Laan and Rose 2011; van der Laan and Robins 2002). We illustrate an example of these methods in the online Appendix B (available at https://ahubb40.github.io/Roadmap/appendix), in which we use data from a different draw of the simulation in this chapter and estimate parameters using a parametric substitution estimator (as illustrated in detail in this chapter), a non-parametric saturated model, a data-adaptive semi-parametric substitution estimator, and a data-adaptive semi-parametric targeted substitution estimator known as targeted maximum likelihood estimation (TMLE). TMLE works by modifying the initial estimator based on data-adaptive fitting of the outcome model, such that the resulting model provides a more targeted bias/variance trade-off for the parameter of interest (van der Laan and Rose 2011). TMLE uses a simple augmentation of the original fit of Ê(Y|A,W), by adding a “clever covariate” that is related to the propensity score, also known as the treatment mechanism Ê(A|W). Informally, one can think of this covariate as capturing residual confounding specific to the parameter of interest. We leave the technical details to other publications (see, for instance, the appendix in van der Laan and Rose 2011), but note that fitting a wider class of models using data-adaptive semi-parametric approaches and targeting to the parameter of interest reduces bias that might result from fitting a simple, and incorrectly specified, parametric model.

Other Parameters and Future Directions

The roadmap approach gives researchers the exciting opportunity to choose the parameter of interest to match the scientific question. Because researchers are unconstrained by usual regression parameters, such as conditional odds ratios, the types of parameters that can be estimated are only constrained by the imagination of the researcher. The list of parameters found in the causal inference literature continues to grow, and a few in particular could be very relevant to social epidemiologists. For example, direct and indirect effects define parameters that relate to pathways of effect or mediation, and could support improved understanding of the chain of events through which distal social factors affect disease outcomes (Hubbard, Jewell, and van der Laan 2011; Pearl 2012; Valeri and VanderWeele 2013). Dynamic interventions define parameters based on exposures that are assigned differentially depending on the covariates of each individual (Cain et al. 2010; Petersen and van der Laan 2011; van der Laan and Petersen 2007). Dynamic interventions could be usefully applied to questions about how alternative ways of changing social exposures, for example, targeted intervention for more vulnerable populations compared with more widespread intervention, would affect health disparities and overall population health. In addition, there is constant innovation on parameter definitions and on how to estimate these parameters (Muñoz and van der Laan 2012; van der Laan 2013). The methods are continuing to evolve and new software tools are being developed that will facilitate implementation.

Conclusions

Overall, the “causal roadmap” approach to scientific endeavors, including the estimation and interpretation of population intervention parameters, has a number of strengths. It necessitates clearly defined scientific questions and ensures the parameters estimated will match the questions posed. It clearly elaborates what assumptions are necessary to interpret a parameter estimated from observed data as a causal effect. Even when assumptions are not met, the ways in which they were not met provide clear guidance on how future research must be improved to increase the potential for causal interpretation. In social epidemiology, we believe that working in a framework that requires a clear statement of the question of interest at the outset will improve the interpretability and relevance of our research. For example, if examining income as an exposure, this framework requires that the researcher specify the amount of income change and for whom. This requirement leads naturally to consideration of feasibility and discussion of ways in which such a change might be achieved. The flexibility to estimate parameters that quantify the population-level impact of specific alterations in the exposure will increase translation of the magnitudes of effects into potential effects of interventions. By working through a specific example and providing statistical code for implementation, it is our hope that this chapter will make this approach more accessible and productively used in research on the social determinants of health.

Acknowledgments

This work was supported in part by the NICHD/NIH Office of the Director (DP2 HD 080350). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

References

1. Ahern, J., Hubbard, A., Galea, S. (2009) Estimating the effects of potential public health interventions on population disease burden: a step-by-step illustration of causal inference methods. American Journal of Epidemiology, 169, 1140–1147. doi: 10.1093/aje/kwp015.
2. Ahern, J., Cerdá, M., Lippman, S.A., et al. (2013a) Navigating non-positivity in neighbourhood studies: an analysis of collective efficacy and violence. Journal of Epidemiology and Community Health, 67, 159–165. doi: 10.1136/jech-2012-201317.
3. Ahern, J., Margerison-Zilko, C., Hubbard, A., Galea, S. (2013b) Alcohol outlets and binge drinking in urban neighborhoods: the implications of nonlinearity for intervention and policy. American Journal of Public Health, 103, e81–87. doi: 10.2105/AJPH.2012.301203.
4. Balzer, L., Petersen, M.L., and van der Laan, M.J. (2014) Adaptive Pair-Matching in the SEARCH Trial and Estimation of the Intervention Effect, University of California Berkeley Division of Biostatistics Working Paper Series. Working Paper 320.
5. Breiman, L., Friedman, J.H., Olshen, R., and Stone, C.J. (1984) Classification and Regression Trees, The Wadsworth Statistics/Probability Series, Wadsworth International Group.
6. Breslow, N. and Day, N. (1987) Statistical Methods in Cancer Research, vol. II: The Design and Analysis of Cohort Studies, Oxford University Press, New York.
7. Cain, L.E., Robins, J.M., Lanoy, E., et al. (2010) When to start treatment? A systematic approach to the comparison of dynamic regimes using observational data. International Journal of Biostatistics, 6, Article 18.
8. Cole, S.R. and Frangakis, C.E. (2009) The consistency statement in causal inference: a definition or an assumption? Epidemiology, 20, 3–5. doi: 10.1097/EDE.0b013e31818ef366.
9. Friedman, J.H. (1991) Multivariate adaptive regression splines (with Discussion). Annals of Statistics, 19, 1–141.
10. Galea, S., 2013. An argument for a consequentialist epidemiology. American Journal of Epidemiology, 178, 1185–1191. doi:10.1093/aje/kwt172
11. Glass, T.A., Goodman, S.N., Hernán, M.A., and Samet, J.M. (2013) Causal inference in public health. Annual Review of Public Health, 34, 61–75. doi: 10.1146/annurev-publhealth-031811-124606.
12. Glymour, M.M., Kawachi, I., Jencks, C.S., and Berkman, L.F. (2008) Does childhood schooling affect old age memory or mental status? Using state schooling laws as natural experiments. Journal of Epidemiology and Community Health, 62, 532–537. doi: 10.1136/jech.2006.059469.
13. Greenland, S. and Drescher, K. (1993) Maximum likelihood estimation of the attributable fraction from logistic models. Biometrics, 49, 865–872.
14. Harper, S. and Strumpf, E.C. (2012) Social epidemiology: questionable answers and answerable questions. Epidemiology, 23, 795–798. doi: 10.1097/EDE.0b013e31826d078d.
15. Hernán, M.A. (2004) A definition of causal effect for epidemiological research. Journal of Epidemiology and Community Health, 58, 265–271.
16. Hernán, M.A., Brumback, B., and Robins, J.M. (2000) Marginal structural models to estimate the causal effect of zidovudine on the survival of HIV-positive men. Epidemiology, 11, 561–570.
17. Hernán, M.A. and Taubman, S.L. (2008) Does obesity shorten life? The importance of well-defined interventions to answer causal questions. International Journal of Obesity, 32 (Suppl. 3), S8–14. doi: 10.1038/ijo.2008.82.
18. Hernán, M.A., and VanderWeele, T.J. (2011) Compound treatments and transportability of causal inference. Epidemiology, 22, 368–377. doi: 10.1097/EDE.0b013e3182109296.
19. Hubbard, A.E., Jewell, N.P., and van der Laan, M.J. (2011) Direct effects and effect among the treated, in Targeted Learning: Causal Inference for Observational and Experimental Data, Springer Series in Statistics, Springer, pp. 133–143.
20. Hubbard, A.E. and van der Laan, M.L. (2008) Population intervention models. Biometrika, 95, 35–47.
21. Kaufman, J.S. (2010) Invited commentary: decomposing with a lot of supposing. American Journal of Epidemiology, 172, 1349–1351; Discussion 1355–1356. doi: 10.1093/aje/kwq329.
22. Kaufman, J.S. and Harper, S. (2013) Health equity: utopian and scientific. Preventative Medicine, 57, 739–740. doi: 10.1016/j.ypmed.2013.09.013.
23. Kessler, R.C., Davis, C.G., and Kendler, K.S. (1997) Childhood adversity and adult psychiatric disorder in the US National Comorbidity Survey. Psychology and Medicine, 27, 1101–1119.
24. Kessler, R.C., McLaughlin, K.A., Green, J.G., et al. (2010) Childhood adversities and adult psychopathology in the WHO World Mental Health Surveys. British Journal of Psychiatry and Journal of Mental Science, 197, 378–385. doi: 10.1192/bjp.bp.110.080499
25. Leslie, H.H., Ahern, J., Chinaglia, M., et al. (2013) Social participation and drug use in a cohort of Brazilian sex workers. Journal of Epidemiology and Community Health, 67, 491–497. doi: 10.1136/jech-2012-202035.
26. Maldonado, G. and Greenland, S. (2002) Estimating causal effects. International Journal of Epidemiology, 31, 422–429.
27. McLaughlin, K.A., Greif Green, J., Gruber, M.J., et al. (2012) Childhood adversities and first onset of psychiatric disorders in a national sample of US adolescents. Archives of General Psychiatry, 69, 1151–1160. doi: 10.1001/archgenpsychiatry.2011.2277.
28. Muñoz, I.D. and van der Laan, M. (2012.) Population intervention causal effects based on stochastic interventions. Biometrics, 68, 541–549. doi: 10.1111/j.1541-0420.2011.01685.x.
29. Nandi, A., Glymour, M.M., Kawachi, I., and VanderWeele, T.J. (2012) Using marginal structural models to estimate the direct effect of adverse childhood social conditions on onset of heart disease, diabetes, and stroke. Epidemiology, 23, 223–232. doi: 10.1097/EDE.0b013e31824570bd.
30. Oakes, J.M. (2004) The (mis)estimation of neighborhood effects: causal inference for a practicable social epidemiology. Society of Science and Medicine, 58, 1929–52.
31. Osypuk, T.L., Tchetgen Tchetgen, E.J., Acevedo-Garcia, D., et al. (2012) Differential mental health effects of neighborhood relocation among youth in vulnerable families: results from a randomized trial. Archives of General Psychiatry, 69, 1284–1294. doi: 10.1001/archgenpsychiatry.2012.449.
32. Pearl, J. (2009) Causality: Models, Reasoning and Inference, 2nd edn, Cambridge University Press, New York.
33. Pearl, J. (2010a) An introduction to causal inference. International Journal of Biostatistics, 6, Article 7. doi: 10.2202/1557-4679.1203.
34. Pearl, J. (2010b) On the consistency rule in causal inference: axiom, definition, assumption, or theorem? Epidemiology, 21, 872–875. doi: 10.1097/EDE.0b013e3181f5d3fd.
35. Pearl, J. (2012) The causal mediation formula—a guide to the assessment of pathways and mechanisms. Preventative Science Office, Journal of Social Preventative Research, 13, 426–436. doi: 10.1007/s11121-011-0270-1.
36. Petersen, M.L., Porter, K.E., Gruber, S., et al. (2012) Diagnosing and responding to violations in the positivity assumption. Statistical Methods in Medical Research, 21, 31–54. doi: 10.1177/0962280210386207.
37. Petersen, M.L., Sinisi, S.E., and van der Laan, M.J. (2006) Estimation of direct causal effects. Epidemiology, 17, 276–284.
38. Petersen, M.L. and van der Laan, M.J. (2011) Case study: longitudinal HIV cohort data, in Targeted Learning: Causal Inference for Observational and Experimental Data, Springer Series in Statistics, Springer, pp. 133–143.
39. Petersen, M.L. and van der Laan, M.J. (2014) Causal models and learning from data: integrating causal modeling and statistical estimation. Epidemiology, 25, 418–426. doi: 10.1097/EDE.0000000000000078.
40. Poole, C. (2010) On the origin of risk relativism. Epidemiology, 21, 3–9.
41. Robins, J. (1986) A new approach to causal inference in mortality studies with a sustained exposure period—application to control of the healthy worker survivor effect. Mathematical Modeling, 7, 1393–1512.
42. Robins, J.M. (1988) Confidence intervals for causal parameters. Statistics in Medicine, 7, 773–785.
43. Robins, J.M. and Rotnitzky, A. (2004) Estimation of treatment effects in randomized trials with noncompliance and a dichotomous outcome using structural nested mean models. Biometrika, 91, 763–783.
44. Rosenbaum, P.R. and Rubin, D.B. (1983) The central role of the propensity score in observational studies for causal effects. Biometrika, 70, 41–55.
45. Rothman, K.J. and Greenland, S. (1998) Modern Epidemiology, 2nd edn, Lippincott-Raven Publishers, Philadelphia, PA.
46. Rothman, K.J., Greenland, S., and Lash, T.L. (2008) Modern Epidemiology, Lippincott Williams & Wilkins.
47. Rubin, D.B. (1980) Comment on “Randomization analysis of experimental data in the Fisher randomization test” by D. Basu. Journal of the American Statistics Association, 75, 591–593.
48. Rubin, D.B. (1986) Statistics and causal inference: Comment: Which ifs have causal answers? Journal of the American Statistics Association, 81, 961–962.
49. Rubin, D.B. (1990) Comment on Neyman (1923) and causal inference in experiments and observational studies. Statistics in Science, 5, 472–480.
50. Sato, T. and Matsuyama, Y. (2003) Marginal structural models as a tool for standardization. Epidemiology, 14, 680–686.
51. Sinisi, S.E., Polley, E.C., Petersen, M.L., et al. (2007) Super learning: an application to the prediction of HIV-1 drug resistance. Statistics in Applied Genetic Molecular Biology, 6, Article7. doi: 10.2202/1544-6115.1240.
52. Valeri, L. and VanderWeele, T.J. (2013) Mediation analysis allowing for exposure–mediator interactions and causal interpretation: theoretical assumptions and implementation with SAS and SPSS macros. Psychological Methods, 18, 137–150. doi: 10.1037/a0031034.
53. van der Laan, M.J. (2012) Causal Inference for Networks, Division of Biostatistics, UC Berkeley Working Paper Series.
54. van der Laan, M.J. (2013) Targeted Learning of an Optimal Dynamic Treatment, and Statistical Inference for its Mean Outcome (No. 317), University of California Berkeley, Division of Biostatistics Working Paper Series.
55. van der Laan M.J., Haight T.J., Tager I.B., et al. (2005) Respond to “hypothetical interventions to define causal effects.” American Journal of Epidemiology, 162, 621–622.
56. van der Laan, M.J. and Petersen, M.L. (2007) Causal effect models for realistic individualized treatment and intention to treat rules. International Journal of Biostatistics, 3, Article 3.
57. van der Laan, M.J., Polley, E.C., and Hubbard, A.E. (2007) Superlearner. Statistics in Applied Genetic Molecular Biology, 6.
58. van der Laan, M.J. and Robins, J.M. (2002) Unified Methods for Censored Longitudinal Data and Causality, Springer, New York.
59. van der Laan, M. and Rose, S. (2011) Targeted Learning: Causal Inference for Observational and Experimental Data, Springer, New York.
60. VanderWeele, T.J. (2008) Ignorability and stability assumptions in neighborhood effects research. Statistics in Medicine, 27, 1934–1943.
61. VanderWeele, T.J. (2009a) On the distinction between interaction and effect modification. Epidemiology, 20, 863–871. doi: 10.1097/EDE.0b013e3181ba333c.
62. VanderWeele, T.J. (2009b) Concerning the consistency assumption in causal inference. Epidemiology, 20, 880–883. doi: 10.1097/EDE.0b013e3181bd5638