CHAPTER EIGHTEEN
USING CAUSAL DIAGRAMS TO UNDERSTAND COMMON PROBLEMS IN SOCIAL EPIDEMIOLOGY

M. Maria Glymour

Social epidemiologists typically seek to answer causal questions using information about associations: we observe an association between poverty and early mortality and seek to determine whether poverty causes early death. An essential component of epidemiologic training is therefore learning when and how causal structures can be inferred from a set of statistical relations. Although the cliché “correlation does not imply causation” is the mantra of introductory epidemiology classes, correlations and other forms of statistical association do give us information about causal relations.

The first step in most causal research should include describing what is already known about the relevant causal structure (Petersen and van der Laan 2014). Causal diagrams are routinely used informally to visually represent beliefs and hypotheses about relations among variables. These informal uses can be greatly expanded by adopting formal rules for drawing the diagrams as causal directed acyclic graphs (DAGs). Causal DAGs provide a simple, flexible device for deducing the associations implied by a given set of assumptions about the causal structure relating variables. We can also move in the other direction: given a set of associations among variables in a sample, we can list the causal structures that could have given rise to these associations. Once the rules for reading off statistical associations from the causal assumptions represented in a DAG are mastered, they facilitate several tasks, for example, choosing covariates to address confounding or recognizing selection bias. Using DAGs helps avoid common mistakes when drawing causal inferences from statistical evidence. The rules linking causal relations to statistical associations are grounded in mathematics, and one advantage of causal diagrams is that they allow non-mathematicians to draw rigorous, mathematically based conclusions about certain types of statistical relations.

Several more comprehensive introductions to DAGs, many written by the researchers who developed the ideas, are available elsewhere (Greenland, Pearl, and Robins 1999; Pearl 2009; Robins 2001; Spirtes, Glymour, and Scheines 2001). The goal of this chapter is to provide a basic introduction to demonstrate the utility of DAGs for applied researchers in social epidemiology.

Some Background Definitions

Before introducing key terms, note that some of the uses adopted here are controversial.1 Debating the definitions is beyond our scope, but little of the discussion of DAGs would be affected by adopting such alternative definitions.

Defining a Cause

Consider two variables, X and Y. We say X causes Y if Y would have taken a different value had X taken a different value than it actually did—and nothing else temporally prior to or simultaneous with X differed. In other words, X is a cause of Y if, had we intervened to change or “set” the value of X to a different value than the one it actually took (but directly intervened on nothing else besides X), then the value of Y would also have differed. To accommodate the possibility that causation is not deterministic (i.e., not all smokers develop lung cancer, even though smoking is a cause of lung cancer), we can say that had X taken a different value, this would have changed the probability distribution for Y. We say that X affects Y in a population if and only if there is at least one individual for whom changing (intervening on) X would change Y.2

Statistical Independence or Dependence

We say X and Y are statistically independent if knowing the value of X does not provide any information about the value of Y (if X is independent of Y, Y is also independent of X). Conversely, we say X and Y are statistically dependent, or statistically associated, if knowing the value of X gives us some information about the likely value of Y, even if this information is very limited and amounts to a modest change in the probability distribution of Y. Statistical dependency may be assessed and quantified with various statistical parameters, for example, regression coefficients, odds ratios, t-tests, chi-squared tests, or correlation coefficients.

Causal Versus Statistical Language

Distinguishing between words that denote causal relations and words that denote statistical relations can be confusing because such words are often used interchangeably in common conversation. “Cause,” “influence,” “change,” “increase,” and “promote” are all causal terms (Pearl 2009). Association, prediction, and any specific measures of association such as regression coefficients, odds ratios, or hazard ratios are statistical terms. Causal relations are intrinsically directed: rainfall makes the ground muddy, but mud does not elicit rainstorms. Statistical associations, however, are not directed: observing rain should make you anticipate mud, and likewise noticing a mud-puddle suggests a recent rainstorm (Pearl 2001).

When an association is reported in an epidemiology article, it is generally with the hope (sometimes unstated) of using this to give insight into a causal relation. Surveillance reports and predictive (as opposed to etiologic) models are exceptions; in these cases, causal inference is not of primary interest.3 Causal inferences usually rely on many more assumptions than do predictive claims, and it is tempting to circumvent critiques of those assumptions by claiming to be exclusively interested in predictive models. Such obfuscations are a disservice to social epidemiology. It is better to acknowledge causal goals and also acknowledge the challenging assumptions, so we can undertake the work needed to evaluate those assumptions.

Causal questions are central in social epidemiology because it is an understanding of causal structures that guides effective interventions to improve public health and eliminate health inequalities. Although inferences about causal structures may often seem unjustified based on available evidence, such inferences are nonetheless typically our long-term goal when conducting etiologic research.

When framing causal questions, it is usually valuable to specify a hypothetical intervention to change the exposure variable. For example, instead of asking “Does income affect diabetes risk among Cherokee tribal members?” we ask “Would sending each tribal member an annual check for $4,000 from the Cherokee Nation government change their diabetes risk?” The effect of such a check might differ from other strategies for changing income—for example, increasing wages or providing in-kind donations or changing tax rates—even if these approaches had identical net monetary value. Most importantly, referring to a hypothetical intervention distinguishes the causal question from related statistical questions, such as “Do high-income Cherokee tribal members have lower diabetes risk compared with low-income Cherokee tribal members?” The hypothetical intervention should directly affect only the exposure X, although other things might also change if they are consequences of exposure. For example, sending a check may affect diet as well as income, but only because recipients use the extra income to buy different foods. Even if it is not possible for the researcher to conduct the intervention, it is nonetheless often clarifying to describe some conceivable way that we could have intervened to alter the value of X.

Conditional Associations

If we examine the distribution of one variable, Y, within levels of a second variable X (e.g., annual mortality risk among people who are unemployed), we say that we are examining the distribution of Y conditional on X. We denote conditional relations with the symbol “|”. Let Pr(Y = y) denote the expected proportion of everyone in the population for whom the variable Y has the specific value y. Stating that X is independent of Y corresponds to saying that, for any specific pair of values x and y for the variables X and Y:

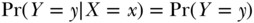
(1) equation

which would be read “the probability that Y = y conditional on X = x (or among those for whom X = x) equals the probability that Y = y in the whole population (i.e., the marginal probability of Y).”4

Similarly, relations between two variables within levels of a third variable—for example, the relation between unemployment and mortality within levels of education—are conditional relations. We may intentionally condition on a variable(s) through features of study design such as restriction or matching, or analytic decisions, such as stratification or regression modeling. Conditioning may arise inadvertently, because some individuals refuse to participate in the study, or drop out or die before the study's conclusion. Such events potentially prevent us from including these individuals in the analysis. Informally, conditioning on a variable is sometimes described as “holding the variable constant,” but this phrase is misleading because it suggests we are actively intervening on the variable, when all we are doing is separating the data into groups based on observed values of the variable and estimating the effects within these groups (and perhaps averaging these estimates over the groups).

If two variables X and Y are statistically independent without conditioning on any other variables, we say X and Y are marginally independent (as in Equation (18.1)). To say that X and Y are independent given Z means that for any values x, y, z for X, Y, and Z,

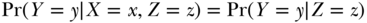
(2) equation

In other words, within any specific value z of Z, knowing the value of X does not provide any information on the value of Y. For example, people who wear neckties may on average be taller than people who do not wear neckties when we consider the whole population, but necktie-wearing and height are likely to be statistically independent conditional on sex.

The Connection Between Causal Structures and Statistical Associations

Although causal dependence and statistical dependence are not the same, they are related phenomena. Specifically, causal structures give rise to statistical associations. Statistical dependency between two variables X and Y could reflect any of five situations (or combinations of these):

  1. Random fluctuation (chance).
  2. X caused Y.
  3. Y caused X.
  4. X and Y share a common cause.5
  5. The statistical association was induced by conditioning on a variable influenced by both X and Y (conditioning on a shared effect is called collider bias, and we discuss it below).

The task epidemiologists typically face is to decide which of these explanations is consistent with our data and background knowledge, and rule out all others. A researcher may begin a study by positing a causal structure, based on background knowledge, and then reason about how to select a set of covariates sufficient to control for confounding in order to identify the magnitude of the effect of interest.

Efforts to discover causal structure may also start more agnostically by describing a set of associations (including both marginal and conditional associations), then describing causal structures that might have given rise to these associations and assessing the logical and statistical compatibility of these structures with the observed associations (potentially noting that some structures are possible but extremely unlikely). Confidence intervals and p-values are used to assess the plausibility that a statistical association is attributable to chance. Temporal order can rule out explanation 3 (reverse causation), and this is why longitudinal studies are advantageous for demonstrating causation. Ruling out shared prior causes, explanation 4, is the goal of most covariate adjustment in regression models. Covariate stratification is also often motivated by the desire to rule out the possibility of common prior causes. Explanation 5—the association was induced by conditioning on a common effect, that is, collider bias —is often ignored. However, collider bias phenomena are important in many settings.

Collider Bias

Why does conditioning on a shared effect of two variables induce a statistical association between those variables? The easiest way to remember this idea is to find a simple anecdote that describes the phenomenon. Suppose you believe that two factors determine basketball prowess: height and speed. Exceptional players must be either extremely tall or extremely fast. If you examined everyone in the world, height and speed might be approximately statistically independent. Short people are not necessarily fast, nor are tall people; however, if you examine only professional basketball players, you would confidently guess that the short ones are very fast. People without the advantage of height must compensate with lightning speed in order to become great ball players.6 When restricting to professional basketball players, we condition on a shared effect of height and speed, and within this stratum of professional ball players, height and speed are (inversely) associated. This is not a perfect association, because some of the tall players are probably also fast. Speed and height may even be correlated in the general population. Whatever the association between speed and height in the general population, it is quite different among professional basketball players (it might even be reversed in ball players compared to the general population). Further, the association observed among the basketball players does not reflect a causal influence of height on speed or vice versa, among ball players or the general population. The inverse association is strictly an artifact of the selection criteria for becoming a professional basketball player. The highly selective criteria to become a professional basketball player has the same causal structure as the selection process for some research studies.

This phenomenon—the change in association between two variables X and Y when conditioning on a third variable Z if Z is affected by both X and Y—is sometimes called collider bias because the two causes “collide” at the common effect. It can be induced by sample selection, stratification, or covariate adjustment if some of the covariates are effects of the other independent variables (Hernán, Hernández-Díaz, and Robins 2004). This phenomenon was first described by Joseph Berkson in 1938 (published in 1946).

Confounding

We say the association between X and Y is biased for the causal effect of X on Y if the association between X and Y does not equal the causal relation between the two variables. This can be described as the distinction between setting and seeing: there is bias if the distribution of Y we would observe by setting X to a particular value does not equal the distribution of Y we see among observations with that value of X. Confounding is a type of bias that arises from particular causal structures,7 typically a shared cause of X and Y. If X and Y are both influenced by Z, the crude (marginal) relation between X and Y is likely to be confounded, although the relation between X and Y conditional on Z may be unconfounded. This matches the conventional intuition that confounding is a “mixing” of effects of two exposures (in this case, X and Z) on a single outcome. If conditioning upon a set of covariates Z will render the association between X and Y unconfounded, then we say Z is a sufficient set of covariates for estimating the relation between X and Y. A sufficient set may be empty (if the crude relation between X and Y is unconfounded) or it may contain one or many variables. There may be several alternative sufficient sets for any pair of variables X and Y (Greenland, Pearl, and Robins 1999; Greenland and Robin 1986).

In counterfactual language, we imagine that each individual has a potential outcome value of Y for each possible exposure value of X, although we observe only one of these possible outcome values of Y (the one that corresponds with the person's actual value of X). If individuals with “good” potential values of Y under either possible value of X are also those individuals who are most likely to receive high values of X, we say the association between X and Y is confounded. For example, consider the impact of attending an Ivy League college on the chance of receiving an inheritance. Suppose the students who attend Ivy League colleges tend to have wealthy parents; such students were likely to be in line for an inheritance regardless of their college selection. In this case, students' potential inheritances will be associated with whether they attend Ivy League colleges. The association between Ivy League college attendance and inheritance receipt will be confounded, and will not equal the causal effect. This intuitive observation is expressed in somewhat less intuitive language by saying that if X is statistically associated with the set of potential outcomes for Y (Yx 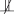image X), the association between X and Y is confounded.

Graphical Models

With this background and common language, we now turn to causal DAGs. Formal introductions to graphical models, explanations of how DAGs relate to conventional structural equation models, and proof of the mathematical equivalence between the rules we apply to DAGs and Robins' g-computation formula can be found elsewhere (Greenland, Pearl, and Robins 1999; Pearl 2009; Spirtes, Glymour, and Scheines 2001; Robins 1987, 1995).

Drawing a Causal DAG

Causal DAGs visually encode an investigator's assumptions about causal relations among the exposure, outcomes, and covariates. In a causal DAG, we say that a variable X causes a variable Y directly (relative to the other variables in the DAG) if there is an arrow from X to Y. We say that X affects Y indirectly if there is a sequence of directed arrows that can be followed from X to Y via one or more intermediate variables. In Figure 18.1, X causes Y directly and Z indirectly. If two variables shown in a DAG share a cause, that common cause must also be included in the DAG or else the DAG is not considered a “causal” graph. It is not necessary to include all causes of individual variables in the DAG; only causes of two or more variables in the DAG must be included. Often, although common causes of two variables in the diagram are suspected to exist, there is considerable uncertainty. This uncertainty should be represented in the causal DAG: possible common causes can be represented as unspecified variables with arrows to the variables they are thought to influence. In a slight modification of these rules, some authors use a two-headed arrow between two variables as a shorthand to indicate that there is at least one unknown common cause of the two variables (e.g., X ↔ Z is used to represent X ← U → Z) (Pearl 2009). Omitting arrows between two variables in a DAG represents a strong assumption.

Overview of the definitions of terminology applied to a DAG, with corresponding casual assumptions and implied independencies.

FIGURE 18.1 DEFINITIONS OF TERMINOLOGY APPLIED TO AN EXAMPLE CAUSAL DAG, WITH CORRESPONDING CAUSAL ASSUMPTIONS AND IMPLIED INDEPENDENCIES

All the graphs we consider are acyclic, which means that they contain no feedback loops. In acyclic graphs no variable is an ancestor or descendant of itself, so if X causes Y, Y cannot also cause X at the same moment. If a prior value of Y affects X, and then X affects a subsequent value of Y, these must each be shown as separate variables (e.g., Y0 → X1 → Y2). For discussions of extensions to causal structures including feedback, see Spirtes (1995), Pearl and Dechter (1996), Lauritzen and Richardson (2002), and Didelez (2008).

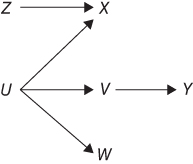
Illustration of DAG showing identification of paths connecting variables and covariates that block paths.

FIGURE 18.2 A DAG TO ILLUSTRATE IDENTIFICATION OF PATHS CONNECTING VARIABLES AND COVARIATES THAT BLOCK PATHS

To apply the d-separation rules to evaluate whether two variables on a causal diagram are statistically associated, one first identifies all paths connecting those two variables. A path can be just one arrow (such as X → Y in Figure 18.1) or a sequence of many arrows (such as Z → X ← U → V → Y as a path between Z and Y in Figure 18.2), but the path cannot cross itself (i.e., no variable can occur more than once on the path). If the arrows in a path all flow in the same direction, the path is considered “directed” (X → Y → Z in Figure 18.1). However, not all paths are directed (the path from Z to Y in Figure 18.2 is not directed: Z → X ← U → V → Y). When there is no arrow or directed path linking two variables in a DAG, this represents the assumption that neither variable affects the other. In Figure 18.1, U and X are only connected by one undirected path, indicating that these two variables do not affect each other. The direction of arrowheads on a path is important to identify variables that are colliders on that path. If arrowheads from X and Y both point to a variable A (as in: X → A ← Y), then A is referred to as a collider on that path between X and Y: the causes collide at A. In other words, a collider is a common effect of two variables on the path (the collider itself must also be on the path). Whether a variable is a collider is specific to a path: it is possible for a variable to be a collider on one path but a mediator or confounder (i.e., not a collider) on another path, even if both paths link the same two variables. By definition, directed paths do not include any collider variables. The direction of arrowheads also helps identify “back-door paths,” which are paths linking an exposure and outcome that originate with an arrow pointing into the exposure. This taps the idea that paths with arrows into X are “back-doors” through which a spurious (non-causal) statistical association between X and Y might arise.

Children of a variable X are variables that are affected directly by X (have an arrow pointing to them from X); conversely, parents of X are variables that directly affect X (have an arrow pointing from them to X). More generally, the descendants of a variable X are variables affected, either directly or indirectly, by X; conversely, the ancestors of X are all the variables that affect X directly or indirectly. In Figure 18.1, Y has parents U and X, and a child Z; X has one child (Y) and two descendants (Y and Z); and Z has a parent Y and three ancestors, Y, U, and X.

DAGs and Structural Equations

DAGs are often conceptualized as non-parametric structural8 equations, with each variable shown in the DAG corresponding to a dependent variable in a structural equation determined by that variable's parents (Petersen and van der Laan 2014; Pearl 2009). Thus, for example, Figure 18.1 implies the following structural equation for Y: Y = fY(X, U, ϵY), where fY( ) is an arbitrary function and ϵY represents all causes or random components of Y not represented in the DAG. Similarly, the DAG implies a structural equation for Z: Z = fZ(Y, ϵZ), which, as specified in the DAG, includes only Y (the only parent of Z) and the unknown-causes error term. The entire DAG could thus be re-expressed as four structural equations, with accompanying information on the independence of the error terms. This connection between DAGs and structural equations is helpful for efforts to simulate data based on a causal DAG. The structural equations specify how to simulate each variable. Noting the connections with structural equations also highlights the lack of information in the DAG; they are completely non-parametric. The above non-parametric structural equation for Y is consistent with countless possible parameterizations for Y, including a simple linear model:

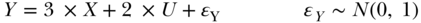
equation

or a log-linear model incorporating an interaction:

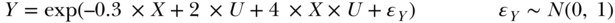
equation

or a model with arbitrary thresholds (letting I( ) represent an indicator function that evaluates to 1 if the statement in ( ) is true):

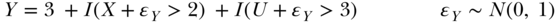
equation

DAGs specify only which variables are parents of one another, not how the parent variables come together to determine the value of a child variable. Now we turn to how much can be learned even from the non-parametric information encoded in a DAG.

The d-Separation Rules Linking Causal Assumptions to Statistical Independencies

The d-separation rules describe the statistical independencies implied by the causal assumptions in a DAG. For example, with a causal DAG representing the null hypothesis that your exposure of interest has no effect on your outcome of interest, plus the assumed causal structure for your covariates, the d-separation rules allow you to check whether, under these assumptions, your exposure and outcome would be statistically independent when conditioning on selected covariate sets.

Specifically, if the assumptions of a causal DAG are correct, then two variables in the DAG will be statistically independent, given the list of covariates, if there are no unblocked paths between the two variables, conditional on that set of covariates. The covariate list may include thousands of variables or none at all. If there are no unblocked paths between X and Y conditional on the covariate set, then X and Y are said to be d-separated and will be independent conditional on that covariate set. How can you tell if a path is blocked by a set of covariates?

A path is blocked by conditioning on a proposed set of variables Z if either of the following two conditions holds: (1) a non-collider on the path is in the set of variables Z or (2) there is a collider on the path, and neither the collider nor any of the collider's descendants is in Z. What if a path includes a collider and also a non-collider and we condition on both? In this situation, the path is blocked.9

These rules fit with the intuition that two variables will be correlated if one causes the other or there is an uncontrolled common prior cause of the two variables. The rules also reflect the potential to induce an association by conditioning on a common effect of two variables (Greenland, Pearl, and Robins 1999; Hernán et al. 2002), as described in the professional basketball example (in which the variable “become a professional basketball player” was a collider on a path linking height and speed).

The definition of d-separation includes situations in which there was no open path before conditioning on Z. For example, a set Z may be sufficient to separate X and Y even if Z includes no variables: if there is no open path between X and Y to begin with, the empty set d-separates them.

Throughout the above discussion, we have referred to the statistical “independencies” implied by the DAG. If we assume “faithfulness,” we can also find the statistical dependencies implied by the DAG: two variables in a DAG will be statistically dependent if there is an unblocked path between them. The faithfulness assumption is that positive and negative causal effects never perfectly offset one another. In other words, if X affects Y through two pathways, and one path increases Y while the other decreases Y, the faithfulness assumption implies that the net statistical relation between X and Y will be either positive or negative, not null. If the two paths perfectly offset one another, the net statistical association would be 0, and we say the statistical associations are unfaithful to the causal relations.

To make these ideas more concrete, consider the example DAG in Figure 18.1. The assumptions encoded in the DAG imply that X and U are marginally independent but become associated after conditioning on either Y or Z. In contrast, X and Z are marginally dependent but become statistically independent after conditioning on Y.

The statistical independencies implied by a causal DAG are only “in expectation,” meaning that they apply to the expected data distribution if the causal structure represented by the graph is correct. Throughout, we assume that statistical associations or lack of associations are not attributable to random variation or chance (that is, we assume a large sample size).10 Formally, the d-separation criteria are based on the intuitively reasonable causal Markov assumption (CMA): any variable X is independent of any other variable Y conditional on the direct causes of X, unless Y is an effect of X.11

Estimating the Causal Effect

Typically our goal is to go beyond simply evaluating if X has any causal effect on Y and estimate the magnitude of such an effect. To estimate the causal effect of X on Y is to contrast the potential values that Y would take if we set X to alternative values. We can do this if we have a set of covariates Z that fulfills the back-door criterion with respect to the effect of X on X. The back-door criterion requires that: (1) no variable in Z is a descendant of X and (2) every path between X and Y that contains an arrow into X is blocked by Z. If a set of variables Z fulfills the back-door criterion for X and Y, we can estimate the distribution of Y if we set X to any specific value x; we do this by by taking the weighted value of Y among individuals with X = x across all strata of Z, with weights equal to the probability of each stratum of Z. More formally:

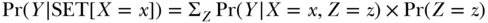
equation

To illustrate, consider Figure 18.2. The variable U blocks all back-door paths between X and Y. Let X represent consumption of red wine, Y represent cardiovascular disease (CVD), and U represent income; this DAG implies that the probability of CVD if we intervened to make someone consume red wine can be calculated provided we have observed information on the joint distribution of income, red wine, and CVD. For simplicity, assume that income can take only three values, low (25% of people), medium (70% of people), and high (5% of people). To estimate the probability of CVD if we forced everyone to drink red wine, we would take the weighted average of the probability of CVD among red wine drinkers with low income (weighted by 0.25), the probability of CVD among red wine drinkers with medium income (weighted by 0.70), and the probability of CVD among red wine drinkers with high income (weighted by 0.05). Estimating the effect of red wine on CVD simply requires repeating the calculation for non-drinkers and comparing predicted CVD probability in the two situations.

Applying DAGs to Guide Analyses in Social Epidemiology

Why are DAGs useful? In general, we wish to test a hypothesis about how the world works within the context of our prior beliefs. This is linked, sometimes implicitly, to a desire to know what would happen if we intervened to change the value of some treatments or exposure. DAGs help answer the question: under my assumptions, would the statistical analysis I am proposing provide a valid test of my causal hypothesis? Consider Figure 18.2 and imagine you are interested in testing whether X has a causal effect on Y (i.e., you are unsure if there should be an arrow from X to Y). Other than this question, you believe the causal structure is as drawn in Figure 18.2. It is immediately evident from the DAG that the analysis must condition on U or V; U confounds the effect of X on Y. However, suppose that you are interested in estimating the effect of Z on Y. In this case, you need not condition on U or V. The relation between Z and Y is unconfounded (as is the relation between Z and X). DAGs provide a way to state explicitly one's prior beliefs about causal relations or alternative sets of plausible prior assumptions. Decisions such as selection of covariates should be based on these priors.

In some cases, the DAGs simply provide a convenient way to express well-understood concepts. In other examples, the DAGs illuminate a point of common confusion regarding the biases introduced by proposed analyses or study designs. The advantage of DAGs is that they provide a simple, flexible tool for understanding an array of different problems.

Deciding Whether to Control for a Covariate

For any analysis, it is important to identify and account for confounders and yet avoid inadvertently controlling for mediators or opening biasing paths by conditioning on colliders. Earlier, we defined bias in terms of contrasting statistical and causal associations. This definition implies graphical criteria for choosing a sufficient set of covariates, which is a set such that within strata of the covariates the statistical relation between exposure and outcome is due only to the effect of exposure on outcome and will be null if the causal effect is null.12 That is, after specifying background causal assumptions using a DAG, we can identify from the DAG a sufficient set of covariates Z for estimating or testing for an effect of X on Y; Z is such a sufficient set if it fulfills the back-door criterion: (1) no variable in Z is a descendant of X and (2) every path between X and Y that contains an arrow into X is blocked by Z. When the back-door criterion is fulfilled by a set of measured covariates, it is possible to estimate the total average causal effect of X on Y.13 (Greenland, Pearl, and Robins 1999; Pearl 2009).

How do the graphical criteria for choosing a sufficient set of covariates relate to traditional criteria for identifying confounders? In both intuition and application, the graphical and conventional criteria overlap substantially. For example, Rothman (2012, p. 137) describes confounding as “the confusion of effects…the effect of the exposure is mixed with the effect of another variable, leading to a bias.” This intuition is similar to the graphical representation of confounding: the effects are “mixed” because there is an open back-door path linking exposure and outcome.

When graphical criteria for confounding are not invoked, variations on the following specific criteria for identifying confounders are frequently suggested (although it is often noted that these criteria do not “define” a confounder):

  1. A confounder must be associated with the exposure under study in the source population.
  2. A confounder must be a risk factor for the outcome, though it need not actually cause the outcome.
  3. The confounding factor must not be affected by the exposure or the outcome.

These conventional rules are based on statistical associations, and we refer to them as the statistical criteria for confounding (a slight misnomer because criterion 3 refers to a causal relation). The statistical criteria often agree perfectly with the back-door criterion—that is, you would choose the same set of covariates using either criteria. For example, in Figure 18.2, both the graphical and statistical criteria indicate that one should condition on U to derive an unbiased estimate of the effect of X on Y. There are cases when the statistical and graphical criteria disagree, however, and when they diverge, it is the statistical criteria that fail.

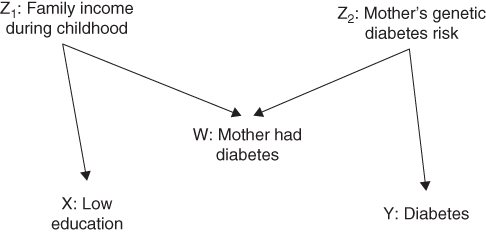
Illustration of DAG showing conventional confounding rules fail.

FIGURE 18.3 A DAG UNDER WHICH CONVENTIONAL CONFOUNDING RULES FAIL

The DAG in Figure 18.3 gives one example. We are interested in whether having low education increases the risk of type II diabetes; the DAG in Figure 18.3 depicts the causal null that education has no effect on diabetes. The mother's diabetes status is measured, but neither family income when the individual was growing up nor the mother's genetic risk of diabetes is measured. Under the assumptions in Figure 18.3, should we adjust our analysis for the mother's diabetes status? The DAG in Figure 18.3 reflects the assumption that family income during childhood affects both educational attainment and the mother's diabetes status. The reasoning is that if an individual was poor as a child, his or her mother was poor as an adult, and this poverty increased the mother's risk of developing diabetes (Robins et al. 2005). The mother's diabetes status will be statistically related to the respondent's education, because under these assumptions they share a cause. The mother's diabetes will also be related to the risk that the respondent has diabetes, because the mother's genetic risk profile affects both her own and her offspring's diabetes risk. The mother's diabetes is not affected by the respondent's own education level or the respondent's own diabetes status. Thus the statistical criteria indicate that the mother's diabetes is a confounder and we should adjust for this variable.

What about the graphical criteria? Would conditioning on the mother's diabetes status block the back-door path between low education and diabetes? There is one path between low education and diabetes, and the mother's diabetes is a collider on that path. If we do not adjust for the mother's diabetes, it blocks the path between our exposure and outcome. Adjusting for the mother's diabetes unblocks this path and induces a spurious statistical association between low education and diabetes. Under the graphical criteria, one should not include the mother's diabetes status as a covariate.

The intuition here is very similar to the reasoning that pro basketball players who are short will tend to be very fast. Assume that mothers developed diabetes owing either to a genetic predisposition or to experiencing poverty as adults (while raising their children). There may be other reasons as well, but assume that these are two non-trivial determinants of a mother's diabetic status. Consider respondents whose mothers had diabetes but no genetic risk factors. These people's mothers are likely to have developed diabetes owing to poverty, implying that the respondents themselves grew up in poverty. Conversely, among respondents with diabetic mothers who did not grow up in poverty, there is probably a genetic risk factor. Conditional on the mother's diabetic status (for example, examining only those whose mothers were diabetic), childhood poverty and genetic risk factors will tend to be inversely related; those whose mothers did not carry a genetic risk factor will tend to have grown up in poverty. Because of this association, among individuals with diabetic mothers, low education will be inversely associated with diabetes risk. If low education increases diabetes risk, adjusting for the mother's diabetic status (under the assumptions in Figure 18.3) will underestimate this effect. This bias will be a problem even if we were to modify the DAG in Figure 18.3 to include an arrow from W to Y (for example, if mother's diabetes influences children's risk via dietary habits). In such a modified DAG, the estimated effect of X on Y is biased in both analyses conditioned on W and in analyses that are not conditioned on W.

The graphical approach to choosing covariates illustrates why there may be several alternative sufficient sets to control confounding. Because a path can be blocked by conditioning on any non-collider on the path, any of several variables might suffice to block an individual path; some of these variables may be easier to measure than others.

A Classification for Types of Bias

In an influential article, Hernán built upon the above perspective on confounding to provide a classification for types of bias that distinguished between non-causal associations due to common causes versus those due to conditioning on a collider (Hernán, Hernández-Díaz, and Robins 2004). He proposed classifying bias arising from a common cause of exposure and outcome (such as the variable U for the association of X and Y in Figure 18.2) to be confounding. This approach includes most of the ways epidemiologists use the term “confounding.” For example, we could imagine that in Figure 18.2, X represents consumption of red wine, Y represents cardiovascular disease (CVD), and U represents income. We would expect a spurious association between wine consumption and CVD due to the common cause of income. Controlling for income would, under the causal assumptions represented in Figure 18.2, eliminate the association between wine consumption and CVD.

In contrast, Hernán proposed that non-causal associations arising from conditioning on a collider be conceptualized as selection bias. Thus, in Figure 18.2, X and U would be associated when conditioning on Z, and this association would be considered a special case of selection bias. This distinction between spurious associations arising from collider conditioning and those arising from common prior causes is a conceptually useful and convenient shorthand when discussing sources of bias. The distinction is not crisp, because in many cases a non-causal association arises from a combination of common prior causes and collider conditioning. Nontheless, this classification scheme clarifies how to handle otherwise ambiguous situations, such as examples of Simpson's paradox (Pearl 2014).

Despite the usefulness of the Hernán framework, it has limitations. For example, using this criterion, defining a “confounder” turns out to be more challenging than defining “confounding.” Not all variables referred to as “confounders” are themselves common prior causes of exposure and outcome. Variables that fall along a back-door path between exposure and outcome, that is, a consequence of a common prior cause of exposure and outcome, such as V in Figure 18.2, are typically considered confounders. Furthermore, proxies of such variables are also often described as confounders if adjusting for them is expected to reduce confounding bias. For example, if W is a proxy for income, say neighborhood average poverty rate, common language in epidemiology would refer to W as a confounder. Even though W is not a common cause of wine consumption and CVD, adjusting for the neighborhood poverty rate may at least partially account for the confounding bias due to income. Hernán and Robins (2016) informally define a confounder as any variable that can help eliminate confounding bias (section 7.3).14

An additional challenge with this framework is that some associations defy easy categorization as due to common causes or collider conditioning. For example, older African Americans are much more likely to have been born in the southern United States than whites of the same age. Regardless of race, individuals born in the south have a higher risk of stroke (Glymour, Avendano, and Berkman 2007). Analyses of the effects of “place of birth” on stroke risk would typically control for race. However, it does not seem satisfactory to represent race as a cause of place of birth in a DAG. Similar concerns arise when representing multiple, correlated, genetic variants on a DAG. A compromise is to represent such factors as correlated, with a correlation that arises from an unspecified common cause. Despite these examples, the overarching representation of confounding as a bias that arises from a common cause of exposure and outcome is extremely useful in most situations.

Why Sample Selection Threatens Internal Validity as Well as Generalizability

Samples for observational epidemiologic studies are drawn using a variety of criteria. The sample may be drawn from a certain occupation (for example, nurses or nuns) or location (for example, Framingham or the Leisure World Laguna Hills retirement community) or patient populations (for example, people with stable coronary heart disease or HIV). Selection criteria can reduce generalizability, as is widely recognized. What is sometimes overlooked, however, is that selection criteria can also affect internal validity; in other words, an exposure–outcome association may be spuriously induced in the sample even when there is no causal effect of exposure on outcome in the very people included in the sample. This potential for bias is of special interest to social epidemiologists, because study sample designs often use criteria that reflect social factors.

On a DAG, we represent selection into the sample as a variable and say that all analyses of a sample are conditioned on selection into that sample. That is, we conceptualize selection as a variable with two values, 0 = not selected and 1 = selected; analyses are restricted to observations for which selection = 1. The value of this selection variable may be influenced by any number of other variables, including the exposure, the outcome, or other factors that influence the exposure, the outcome, or both. Selection bias may occur if the likelihood of being admitted to the sample depends on both the exposure and the outcome or their respective causes.

To illustrate with an extreme example, imagine a study of the effect of education on Alzheimer's disease (AD). Suppose the eligibility criteria for the study are (1) college education or higher or (2) memory impairment. Within the sample, you find a strong inverse correlation between education and AD. In fact, everyone with less than a college education has memory impairment (the harbinger of AD), because otherwise they would not have been eligible for the study. All the sample members with good memory turn out to have high education. Thus, in this sample, higher education is associated with lower risk of AD. Obviously, this is a completely spurious statistical association, induced by conditioning sample membership on education and memory impairment. All analyses of the sample are conditional on sample membership, and sample membership is a shared effect of the exposure and outcome of interest. No matter what the causal relation between education and AD, the statistical associations in the selected sample will differ substantially.

The bias in this example did not result from drawing a non-representative sample from the “target population” and was not simply a problem of generalizability. This bias would arise even if the target population were defined to be “college graduates or those with memory impairment”; this definition compromises the internal validity of causal effect estimates for the people included in the sample, even if the sample is representative of the target population. Within this population the statistical associations between education and AD will not equal the causal effect for that population.

This example is obvious because the selection criteria were direct measures of the exposure and outcome. However, selection may be more subtly related to factors that influence exposure and outcome. The strength of the spurious association induced by selection bias will depend on the details of the selection process, that is, how strongly the factors affect participation and whether they interact in any way to determine study enrollment. Bias due to selection is not necessarily resolved by using a longitudinal study design.

Telling the story as in the preceding paragraphs is complicated, but analyzing the DAG is quite straightforward. Given the DAG in Figure 18.4, S is a collider between X and U; so X and U are statistically associated conditional on S, even under the null hypothesis represented in this DAG. Whether selection exacerbates or reduces bias in a specific causal estimate depends crucially on the causal relations among variables determining selection. If we added an arrow from U to X to the DAG in Figure 18.4, selection on S might reduce bias in estimating the effect of X on Y.15

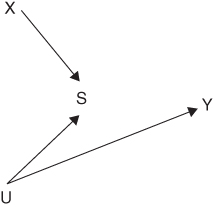
Illustration of DAG for selection bias.

FIGURE 18.4 A DAG FOR SELECTION BIAS

Selection bias is common in research in patient populations, for example, when the scientific question of interest relates to the determinants of prognosis among individuals diagnosed with heart failure or arthritis. This question must be assessed within a sample restricted to diagnosed patients, but such restriction may introduce spurious associations with outcomes. For example, low education is often observed to predict slower memory declines among individuals diagnosed with AD, although low education is a risk factor for the onset of dementia (Stern et al. 1999). Obesity predicts lower mortality among individuals diagnosed with heart failure (Curtis et al. 2005). These surprising associations may reflect spurious associations between the risk factor and other (unmeasured) causes of disease progression induced by restricting analyses to patients (Banack and Kaufman 2014).

Survivor bias can be thought of as arising from the same process that leads to selection bias.16 In life-course research on early life exposures and health in old age, a large fraction of the exposed are likely to die before reaching old age, so survivor bias could be influential. Effect estimates for many exposure–outcome combinations are larger among the young and middle-aged than among the old (Kaplan, Haan, and Wallace 1999; Howard and Goff 1998). An especially striking example of this phenomenon is the black–white mortality crossover: mortality is greater for blacks and other disadvantaged groups relative to whites at younger ages, but the pattern reverses at the oldest ages (Corti et al. 1999; Thornton 2004).

Does the diminishing magnitude of effect estimates among the elderly indicate that the early life exposures become less important causes of the outcome among the old? This would be a very important substantive finding, suggesting that social determinants were less important for older adults and that the injustices leading to disparities through most of the life course dissipated in old age. However, this inference of diminished effects is not necessarily supported by attenuated associations in older samples (Howard and Goff 1998; Mohtashemi and Levins 2002). In a selected group of individuals who survive to old age, observed coefficients for early life exposures may differ from the causal coefficients if the following criteria are fulfilled: (1) probability of survival is influenced by early life exposure and some other unmeasured factor, (2) the effects of the unmeasured factor and early life exposure on survival are not perfectly multiplicative,17 and (3) the unmeasured factor influences the outcome of interest. This can occur even if the unmeasured factor is statistically independent of exposure at birth and thus would not be considered a confounder.

Consider a simple example of this phenomenon for the causal question of the effect of mother's socioeconomic status (SES) affects stroke risk. We enroll 60-year-olds in 1980 (the 1920 birth cohort); by this age about 40% of the birth cohort has died (Arias 2004). Suppose that having a low SES mother doubled the risk of death before age 60. There is a genetic variant that doubles again the risk of mortality before age 60, but the gene has mortality effects only among people with low SES mothers. Even if mother's SES and the genetic variant were independent at birth, these two risk factors will be associated among people who survive to age 60 (the genetic variant will be less common among people with low SES mothers). Suppose that a high SES actually had no effect on stroke risk after age 60 (that is, if, for everybody in the sample, we intervened to alter their mother's SES, this would not alter their stroke outcome) but the genetic variant increases stroke risk regardless of one's mother's SES. Even under this assumption of no causal effect of SES, we would observe that high-SES survivors to age 60 have an elevated risk of subsequent stroke compared with low-SES survivors. Although the spurious statistical association between SES and stroke would vanish within the strata of the genetic allele, the crude SES–stroke association is biased. Even if the causal effect is not null, whatever protection (or risk) having a high-SES mother might have conferred against having a stroke after age 60, the association between maternal SES and stroke will be biased toward looking harmful among the survivors.

The potential for survivor bias described above can be immediately recognized from a causal DAG with the structure in Figure 18.4, letting S represent survival, affected by the mother's SES (X) and a gene (U) that also affects stroke (Y). The direction and magnitude of the bias can be estimated under various assumptions about the causal structure, although the assumptions needed are more detailed than those shown in DAGs (Chiba and VanderWeele 2011; Glymour and Vittinghoff 2014; Mayeda et al. 2016). Sometimes the plausible range of the bias may be too small to be of concern, but this is not always the case.18

Representing Exposures Not Amenable to Experimental Intervention on a DAG

Many variables of interest to social epidemiologists, such as race, sex, genetic ancestry, or region of birth, are not easily amenable to interventions. Although one can sometimes posit an intervention to modify such variables (e.g., sex reassignment surgery), these interventions often do not correspond with what researchers imagine when they seek to quantify “the effect of being female,” which might include lifelong biological differences triggered by carrying two X chromosomes, gendered social interactions and expectations, and physiologic changes subsequent to the gendered world women and men inhabit.

In some cases plausible interventions modify a closely associated construct. For example, audit studies randomly assign stereotypically male or female names to otherwise identical résumés (Darity and Mason 1998) and monitor whether these résumés elicit different responses when submitted to job postings. Similar approaches have been used to evaluate discrimination against African Americans (Bertrand and Mullainathan 2004). Although this provides a brilliant strategy for evaluating a narrow range of effects of being perceived as female or African American, it only captures one pathway via which sex and race are linked to outcomes, and does not solve the essence of the challenge in determining the causal effect of sex or race.

The question of whether non-modifiable variables can be considered “causal” under a counterfactual definition of causation has long been controversial (Holland 1986a, 1986b; Glymour 1986; Kaufman and Cooper 1999; VanderWeele and Robinson 2014a, 2014a; Glymour and Glymour 2014). The counterfactual definition of the effect of being female on risk of depression assumes the existence, for each woman, of a potential outcome for depression that she would have had if she were male. Holland famously argued that “causes are only those things that could, in principle, be treatments in experiments,” including hypothetical experiments.19 He therefore ruled out the possibility of considering race or sex as causes (Holland 1986a). We call this the “No Manipulation, No Causation” (NMNC) viewpoint.

Holland's influential argument commonly elicits variants on one of four responses from social epidemiologists. Some social epidemiologists are receptive to the NMNC perspective on the grounds that it forces us to focus not on race and sex as innate individual characteristics, but on the social construction and consequences of race and sex—including the discriminatory experiences differentially encountered by racial minorities and women—and other modifiable mechanisms hypothesized to lead to health inequalities (Zuberi and Bonilla-Silva 2008). These researchers often emphasize the malleability and ambiguity of self- and other-perceived race based on the social context (Saperstein and Penner 2012), implying that effects of these variables may not be estimable on an individual level (Krieger 2014).20 Other researchers embrace the NMNC view, reasoning that characteristics such as race or sex are such fundamental features of an individual that it is unimaginable to contemplate the same person's outcomes if he or she were of a different race or sex (Kaufman and Cooper 2001).21

Some researchers adopt a weak NMNC position that, although in theory variables that do not correspond with clear interventions can be causes, we simply cannot learn anything about the effects of these variables from observational data (and, by definition, we shall never have intervention-based evidence) (Hernán 2016). Because the regression contrasts do not correspond with a conceivable intervention, they cannot be said to correspond with the “effect” of race or sex, merely the associations between race/sex and health. These researchers sometimes allow that although one cannot identify the effect of race, the effects of mediators between race and health, such as income, might be identifiable (VanderWeele and Robinson 2014a; Naimi and Kaufman 2015).

In the final camp are researchers (including this author) who either reject the NMNC notion entirely or weaken the requirement for an intervention so that nothing of interest is ruled out.22 Many variables for which we do not envision experimental interventions, including sex and race, are nonetheless “causal” for numerous outcomes. Acknowledging the widespread health consequences of race and sex will advance efforts to identify mechanisms and eliminate inequalities. The importance of modifiable social pathways such as discrimination in linking race and sex to health outcomes does not render race or sex non-causal. Rather, the importance of these mechanisms guides our perspectives on the injustice of inequalities and efforts to identify appropriate public health responses to eliminate disparities. Although the fluidity of meaning ascribed to constructs such as race and sex has profound implications for the interpretation of observed disparities, it does not render these constructs any less powerful determinants of health.23

Regardless of their positions on the above controversy, researchers from all four positions may need to represent non-manipulable variables in DAGs (VanderWeele and Robertson 2014a; Glymour and Spiegelman 2016). There is general consensus that it is acceptable to represent sex and race in DAGs and show arrows from race and sex to other variables, for example, discrimination or depression. There is also broad consensus that such variables can be confounders and that representing the variables in a DAG can help identify biasing pathways for other effects of interest.

In most cases, “non-manipulable” variables will not have any causes and therefore will not have arrows pointing into them. There are a handful of exceptions. For example, sex ratios of newborns are thought to vary slightly in response to environmental conditions (e.g., temperature, terrorist attacks, economic turmoil, or wars), so for some research it may be useful to include such stressors as causes of sex (Catalano, Bruckner, and Smith 2008). As discussed above, there are vast differences in racial composition of geographic regions. Although we may not consider “place of birth” a cause of one's race, the majority of older African Americans were born in the Southern United States. People born in the south have a higher risk of many health outcomes, regardless of race, and so it is a potential confounder for many studies of race and health. We suggest either representing the association between place of birth and race on a DAG using an unspecified double-headed arrow or representing an indicator of the legacy of inequality (ancestors were held in bondage in a southern state) as a common cause of place of birth and race. For example, Robinson and VanderWeele represent history as “a complex historical process that gives rise to associations of a person's physical phenotype, parental physical phenotype, and genetic background with the family and neighborhood socioeconomic status into which the person was born” as a variable on a DAG (VanderWeele and Robinson 2014a, p. 475). Such representations may not settle the NMNC debate, but suffice to allow us to think coherently about possible confounders in many analyses.

Representing Measurement Error

The variables measured and made available for analysis often fail to correspond perfectly to the latent constructs of scientific interest. We want a comprehensive account of economic resources, including precise asset values, income from social insurance, earned wages, etc. Instead of this comprehensive measure, we have a single item with six income brackets, which the respondent may not have selected accurately. Lack of correspondence between the construct of interest and the measurement can result in bias.

These situations are easily illustrated in DAGs by showing the latent value and the measured values as separate variables and including measurement error as a variable in the DAG. Specifically, if the measurement error of X depends on Y or a determinant of Y, there will be a statistical association between measured X and Y, even in the absence of a causal effect of (true) X on Y. Similarly, if X or a cause of X influences the measurement error in Y, we expect a spurious association to emerge (Figure 18.5). When distinguishing between latent and measured variables on a DAG, it is typical to include the error term as a variable, following the conventions of structural equation models.

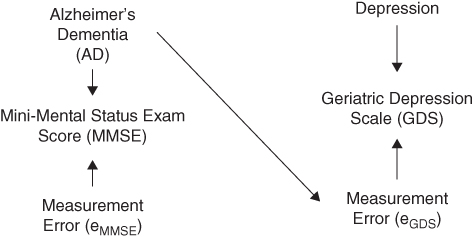
Illustration of the measured value of MMSE.

FIGURE 18.5 AN EXAMPLE ILLUSTRATING INCLUSION OF A MEASUREMENT ERROR IN EXPOSURE AND OUTCOME, WITH THE OUTCOME MEASUREMENT ERROR INFLUENCED BY THE VALUE OF THE EXPOSURE

Representing error terms in the DAG entails a deterministic relation: the measured value of MMSE in Figure 18.5 is perfectly determined by the combination of the latent value of AD and the measurement error for MMSE (eMMSE). When deterministic associations are represented on a DAG, the d-separation rules still apply in that statistical independencies imply the absence of causal effects, but there may be additional statistical dependencies that are not implied by the causal structure. Regardless, with the measurement error represented as a variable in the DAG, the d-separation rules can be used to answer the key question: “under the null hypothesis that X does not affect Y, would measured X be independent of (d-separated from) measured Y?” Often the magnitude of bias introduced by the measurement error is specific to the particular parameter being estimated (e.g., a linear regression coefficient or an odds ratio). Because the DAGs are non-parametric, they provide no insight into how these estimand-specific biases operate and whether they would inflate, deflate, or not affect parameter estimates. Enhancements such as assigning signs to paths in DAGs can provide more insight, at least regarding the direction of bias (VanderWeele and Hernán 2012). DAGs are most helpful for understanding potential impacts of measurement error when we focus on the null hypothesis of no causal effect, because the unbiased effect estimate under the null is always null, regardless of whether estimates are characterized using linear regression, odds ratios, or some other statistical parameter (Hernán and Cole 2009).

Caveats and Conclusion

Directed acyclic graphs do not convey information about important aspects of the causal relations, such as the magnitude or functional form of the relations (for example, linearity, interactions, or effect modification). One consequence of the lack of parametric assumptions is that the effects of interest may not be identified in a DAG, when they might be identifiable with additional (parametric) assumptions, such as linearity. This can be frustrating because not all biases are created equal, and some can safely be ignored. For example, collider bias is often small (Greenland 2003). In some cases, formulas for the magnitude of potential bias are available. Sometimes simulations are needed because the data generating structure is more complex than accommodated by the formulas (Mayeda et al. 2016; Glymour et al. 2015).

Drawing a DAG that adequately describes our prior beliefs or assumptions is sometimes difficult. To the extent that using DAGs forces greater clarity about assumptions, this seems advantageous. Uncertainty about how to specify the DAG implies uncertainty about the causal interpretation of statistical tests.

Directed acyclic graphs are a convenient device for expressing ideas explicitly and understanding how causal relations translate into statistical relations. Causal DAGs provide a simple, flexible tool to represent many apparently disparate problems in epidemiologic reasoning. Although it is possible to draw an utterly confused DAG, more commonly DAGs help articulate implicit conceptual models and incorporate subject matter expertise. Consistent use of causal diagrams may help us recognize when the statistical models deployed to address a research question could not identify the effect of interest under any plausible causal model. Honest use of causal diagrams to represent uncertainty—although likely to be humbling because there are frequently a dizzying number of plausible DAGs—can also help identify valuable incremental advances when an analysis eliminates some, but not all, competing causal hypotheses. Finally, clear explication of causal DAGs in observational research may help us recognize the statistical evidence necessary to guide interventions, so our effect estimates correspond with the likely consequences of proposed interventions.

Acknowledgments

The earlier edition of this chapter was substantially reconceptualized and rewritten in collaboration with Sander Greenland and published in Modern Epidemiology, 3rd edition (Glymour and Greenland 2008). The current chapter owes a great debt to Dr Greenland for that collaboration and subsequent comments. The author also thanks Dr Tyler VanderWeele for helpful comments on a draft.

References

  1. Arias, E. (2004) United States Life Tables, 2001. National Vital Statistics Reports, 52 (14), 1–38.
  2. Banack, H.R. and Kaufman, J.S. (2014) The obesity paradox: understanding the effect of obesity on mortality among individuals with cardiovascular disease. Preventive Medicine, 62, 96–102.
  3. Berkson, J. (1946) Limitations of the application of fourfold table analysis to hospital data. Biometrics Bulletin, 2 (3), 47–53.
  4. Bertrand, M. and Mullainathan, S. (2004) Are Emily and Greg more employable than Lakisha and Jamal? A field experiment on labor market discrimination. The American Economic Review, 94 (4), 991–1013.
  5. Bollen, K.A. and Pearl, J. (2013) Eight myths about causality and structural equation models, in Handbook of Causal Analysis for Social Research, Springer, pp. 301–328.
  6. Catalano, R., Bruckner, T., and Smith, K.R. (2008) Ambient temperature predicts sex ratios and male longevity. Proceedings of the National Academy of Sciences of the United States of America, 105 (6), 2244–2247.
  7. Chaix, B., Evans, D., Merlo, J., et al. (2012) Commentary: weighing up the dead and missing: reflections on inverse-probability weighting and principal stratification to address truncation by death. Epidemiology, 23 (1), 129–131.
  8. Chiba, Y. and VanderWeele, T.J. (2011) A simple method for principal Strata effects when the outcome has been truncated due to death. American Journal of Epidemiology, 173 (7), 745.
  9. Corti, M.C., Guralnik, J.M., Ferrucci, L., et al. (1999) Evidence for a Black-White crossover in all-cause and coronary heart disease mortality in an older population: The North Carolina EPESE. American Journal of Public Health, 89 (3), 308–314.
  10. Curtis, J.P., Selter, J.G., Wang, Y., et al. (2005) The obesity paradox: body mass index and outcomes in patients with heart failure. Archives of Internal Medicine, 165 (1), 55–61.
  11. Darity, W.A. and Mason, P.L. (1998) Evidence on discrimination in employment: codes of color, codes of gender. The Journal of Economic Perspectives, 63–90.
  12. Dawid, A.P. (2000) Causal inference without counterfactuals. Journal of the American Statistical Association, 95 (450), 407–424.
  13. Didelez, V. (2008). Graphical models for marked point processes based on local independence. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 70 (1), 245–264.
  14. Glymour, C. (1986) Statistics and causal inference—Statistics and metaphysics. Journal of the American Statistical Association, 81 (396), 964–966.
  15. Glymour, C. and Glymour, M.R. (2014) Commentary: race and sex are causes. Epidemiology, 25 (4), 488–490.
  16. Glymour, C., Scheines, R., Spirtes, P., et al. (2015) The Tetrad Project: Causal Models and Statistical Data. The Tetrad Project. Available at: www.phil.cmu.edu/projects/tetrad (Accessed 6/12/2016).
  17. Glymour, M.M., Avendano, M.P., and Berkman, L.F. (2007) Is the stroke belt worn from childhood? Risk of first stroke and state of residence in childhood and adulthood. Stroke, 38 (9), 2415–2421.
  18. Glymour, M.M. and Greenland, S. (2008). Causal diagrams, in Modern Epidemiology, 3rd edition (eds K.J. Rothman KJ, S. Greenland, T.L. Lash), Lippincott Williams & Wilkins, Philadelphia, PA, pp. 183–210.
  19. Glymour, M.M., Osypuk, T.L., and Rehkopf, D.H. (2013) Invited commentary: off-roading with social epidemiology—exploration, causation, translation. American Journal of Epidemiology, 178 (6), 858–863.
  20. Glymour, M.M. and Spiegelman D (2016) Valuating Public Health Interventions: 5. Causal inference in public health research: do sex, race, and biological factors cause health outcomes? American Journal of Public Health. forthcoming.
  21. Glymour, M.M. and Vittinghoff, E. (2014) Commentary: selection bias as an explanation for the obesity paradox: just because it's possible doesn't mean it's plausible. Epidemiology, 25 (1), 4–6.
  22. Greenland, S. (2003) Quantifying biases in causal models: classical confounding vs collider-stratification bias. Epidemiology, 14 (3), 300–306.
  23. Greenland, S., Pearl, J., Robins, J.M. (1999) Causal diagrams for epidemiologic research. Epidemiology, 10 (1), 37–48.
  24. Greenland, S. and Robins, J.M. (1986) Identifiability, exchangeability, and epidemiological confounding. International Journal of Epidemiology, 15 (3), 413–419.
  25. Hernán, M. and Robins, J. (2016) Causal Inference, Chapman & Hall/CRC, Boca Raton, FL (forthcoming). Available at https://www.hsph.harvard.edu/miguel-hernan/causal-inference-book/
  26. Hernán M.A. (2016) Does water kill? A call for less casual causal inferences. Annals of Epidemiology, 10, 674–680.
  27. Hernán, M.A. and Cole, S.R. (2009) Invited commentary: causal diagrams and measurement bias. American Journal of Epidemiology, 170 (8), 959–962.
  28. Hernán, M.A., Hernández-Díaz, S., and Robins, J.M. (2004) A structural approach to selection bias. Epidemiology, 15 (5), 615–625.
  29. Hernán, M.A. and Taubman, S.L. (2008) Does obesity shorten life? The importance of well-defined interventions to answer causal questions. International Journal of Obesity, S8–S14.
  30. Hernán, M.A., Hernández-Díaz, S., Werler, M.M., et al. (2002) Causal knowledge as a prerequisite for confounding evaluation: an application to birth defects epidemiology. American Journal of Epidemiology, 155 (2), 176–184.
  31. Holland, P.W. (1986a) Statistics and causal inference. Journal of the American Statistical Association, 81 (396), 945–960.
  32. Holland, P.W. (1986b) Statistics and causal inference—Rejoinder. Journal of the American Statistical Association, 81 (396), 968–970.
  33. Holland, P.W. (2003) Causation and Race, Educational Testing Service, Princeton, NJ.
  34. Howard, G. and Goff, D.C. (1998) A call for caution in the interpretation of the observed smaller relative importance of risk factors in the elderly. Annals of Epidemiology, 8 (7), 411–414.
  35. Hulley, S.B., Cummings, S.R., Browner, W.S., et al. (2013) Designing Clinical Research, Lippincott Williams & Wilkins, Philadelphia, PA.
  36. Kaplan, G.A., Haan, M.N., and Wallace, R.B. (1999) Understanding changing risk factor associations with increasing age in adults. Annual Review of Public Health, 20, 89–108.
  37. Kaufman, J. and Cooper, R. (1999) Seeking causal explanations in social epidemiology. American Journal of Epidemiology, 150 (2), 113–120.
  38. Kaufman, J.S. and Cooper, R.S. (2001) Commentary: considerations for use of racial/ethnic classification in etiologic research. American Journal of Epidemiology, 154 (4), 291–298.
  39. Krieger, N. (2014) Discrimination and health inequities, in Social Epidemiology (eds L.F., Berkman, I. Kawachi, and M.M. Glymour), Oxford University Press, New York.
  40. Lauritzen, S.L. and Richardson, T.S. (2002) Chain graph models and their causal interpretations. Journal of the Royal Statistical Society, Series B–Statistical Methodology, 64, 321–348.
  41. Mayeda, E., Tchetgen Tchetgen, E.J., Power, M., et al. (2016) A simulation platform to quantify survival bias: an application to research on determinants of cognitive decline. American Journal of Epidemiology, 184 (5), 378–387.
  42. Miller, J.B. and Sanjurjo, A. (2015) Surprised by the Gambler's and Hot Hand Fallacies? A Truth in the Law of Small Numbers. IGIER Working Paper. Available at: http://ssrn.com/abstract=2627354 or http://dx.doi.org/10.2139/ssrn.
  43. Mohtashemi, M. and Levins, R. (2002) Qualitative analysis of the all-cause Black–White mortality crossover. Bulletin of Mathematical Biology, 64 (1), 147–173.
  44. Naimi, A.I. and Kaufman, J.S. (2015) Counterfactual theory in ocial epidemiology: reconciling analysis and action for the social determinants of health. Current Epidemiology Reports, 2 (1), 52–60.
  45. Pearl, J. (2001) Causal inference in the health sciences: a conceptual introduction. Health Services and Outcomes Research Methodology, 2, 189–220.
  46. Pearl, J. (2009) Causality: Models, Reasoning, and Inference, 2nd edn, Cambridge University Press, Cambridge, UK.
  47. Pearl, J. (2014) Comment: understanding Simpson's paradox. The American Statistician, 68 (1), 8–13.
  48. Pearl, J. and Dechter, R. (1996) Identifying independencies in causal graphs with feedback. Presented at the 12th Conference on Uncertainty in Artificial Intelligence, San Francisco, CA.
  49. Pearl, J., Glymour, M., and Jewell, N.P. (2016) Causal Inference in Statistics: A Primer, John Wiley & Sons.
  50. Petersen, M.L. and van der Laan, M.J. (2014) Causal models and learning from data: integrating causal modeling and statistical estimation. Epidemiology (Cambridge, Mass.), 25 (3), 418–426.
  51. Robins, J. (1987) A graphical approach to the identification and estimation of causal parameters in mortality studies with sustained exposure periods. Journal of Chronic Diseases, 40 (Suppl. 2), 139S–61S.
  52. Robins, J.M. (1995) Comment on Judea Pearl's paper, “Causal diagrams for empirical research.” Biometrika, 82, 695–698.
  53. Robins, J.M. (2001) Data, design, and background knowledge in etiologic inference. Epidemiology, 12 (3), 313–320.
  54. Robins, J.M., Vaccarino, V., Zhang, H., et al. (2005) Socioeconomic status and diagnosed diabetes incidence. Diabetes Research on Clinical Practice, 68 (3), 230–236.
  55. Rothman, K. (2012) Epidemiology: An Introduction, 2nd edn, Oxford University Press, New York.
  56. Saperstein, A. and Penner, A.M. (2012) Racial fluidity and inequality in the United States. American Journal of Sociology, 118 (3), 676–727.
  57. Shardell, M., Hicks, G.E., and Ferrucci, L. (2015) Doubly robust estimation and causal inference in longitudinal studies with dropout and truncation by death. Biostatistics, 16(1), 155–168.
  58. Spirtes, P. (1995) Directed cyclic graphical representation of feedback. Presented at the 11th Conference on Uncertainty in Artificial Intelligence, San Mateo, CA.
  59. Spirtes, P., Glymour, C., and Scheines, R. (2001) Causation, Prediction, and Search, 2nd edn, MIT Press, Cambridge, MA.
  60. Stern, Y., Albert, S., Tang, M.-X., et al. (1999) Rate of memory decline in AD is related to education and occupation: cognitive reserve? Neurology, 53 (9), 1942–1947.
  61. Tchetgen Tchetgen, E.J., Glymour, M.M., Shpitser, I., et al. (2012) Rejoinder: To Weight or Not to Weight? on the relation between inverse-probability weighting and principal stratification for truncation by death. Epidemiology, 23 (1), 132–137.
  62. Thornton, R. (2004) The Navajo–US population mortality crossover since the mid-20th century. Population Research and Policy Review, 23 (3), 291–308.
  63. Vandenbroucke, J.P., Broadbent, A., and Pearce, N. (2016) Causality and causal inference in epidemiology: the need for a pluralistic approach. International Journal of Epidemiology. Available at http://ije.oxfordjournals.org/cgi/pmidlookup?view=long&pmid=26800751
  64. VanderWeele, T.J. and Hernán, M.A. (2012) Results on differential and dependent measurement error of the exposure and the outcome using signed directed acyclic graphs. American Journal of Epidemiology, 175 (12), 1303–1310.
  65. VanderWeele.T.J. and Robinson, W.R. (2014a) On the causal interpretation of race in regressions adjusting for confounding and mediating variables. Epidemiology, 25 (4), 473–484.
  66. VanderWeele, T.J. and Robinson.W.R. (2014b) Rejoinder: How to reduce racial disparities?: Upon what to intervene? Epidemiology, 25 (4), 491–493.
  67. VanderWeele, T.J. and Shpitser, I. (2013) On the definition of a confounder. Annals of Statistics, 41 (1), 196–220.
  68. Zuberi, T. and Bonilla-Silva, E. (2008) White Logic, White Methods: Racism and Methodology, Rowman & Littlefield Lanham, MD.