CHAPTER FOUR
Multiple Cash Flows
If the investment pays interest periodically, the FV can be calculated as a series of simple interest problems, as shown in Figure 4.1.
FIGURE 4.1
Calculating FV on Investments That Pay Periodically

FOR PERIOD 1:
PV = $1,000,000
I = PV × R × T
I = $1,000,000.00 × .10 × 181 / 365
I = $49,589.04
PV = $1,000,000 + $49,589.04
I = PV × R × T
I = $1,049,589.04 × .1 × 184 / 365
I = $52,910.79
FOR PERIOD 3:
PV = $1,049,589.04 + $52,910.79
I = PV × R × T
I = $1,102,499.83 × .1 × 181 / 365 = $54,671.91
FOR PERIOD 4:
PV = $1,102,499.83 + $54,671.91
I = PV × R × T
I = $1,157,171.74 × .1 × 184/365
I = $58,334.14
The FV = $1,215,505.88, and the total interest earned is, therefore, $215,505.88.
Calculating Long-Term Returns
While this methodology will always work, it is impractical for long-term problems. Who wants to break a 30-year semiannual bond problem into 60 simple interest problems?
If, and only if, the investment vehicle uses a 30/360 calendar convention and the investment term is equal to a whole number of compounding periods, then the PV, I, and FV can be calculated using the equation shown in Figure 4.2.
Calculate FV Using Periodic Compounding
FV = PV(1 + i)n
WHERE:
n = number of compounding periods
i = interest rate per compounding period
PV = the number of dollars that are invested
FV = the principal plus the interest at the end of the investment
The equation shown in Figure 4.2 can always be solved using any calculator with an exponent function. (Sometimes it is easier to use the exponent key to solve simple PV/FV problems than it is to use the specialized PV/FV keys.) The HP-12C financial calculator includes a set of keys which are pre-programmed to solve PV/FV equations. The use of these keys is described in Figure 4.3.
FIGURE 4.3
Excel and HP-12C Inputs for PV/FV Calculations
|
Key |
Notes |
|
n |
The total # of compounding periods over the life of the investment |
|
i |
Interest rate per period (the annual stated interest rate divided by the number of periods per year) |
|
PV |
The amount invested (entered as a negative number) |
|
PMT |
For zero coupon bond problems—set to zero |
|
FV |
Future value of the investment |
The following examples illustrate both methodologies of solving simple finite compounding problems.
PROBLEM 4A
You invest $1MM in a 10% 5-year investment which pays interest annually and is quoted on a 30/360 calendar. What is the future value?
ANSWER:
FV = PV(1 + i)n
FV = $1MM(1 + .1)5
FV = $1,610,510
Keystrokes using exponent key:
1 [ENTER]
.1 +
5 yx
1,000,000 ×
$1,610,510
Keystrokes using PV/FV keys:
5 [n]
10 [i]
1,000,000 [CHS] [PV]
0 [PMT]
[FV]
PROBLEM 4B
How much would you have to invest today in order to have $5MM in 20 years? Assume you could invest in a vehicle investment that compounds semiannually at 8% on a 30/360 calendar.
FV = PV(1 + i)n
$5MM = PV[1 + .08 / 2]40
$5MM = PV(1 + .04)40
$5MM = 4.08010206PV
PV = $1,041,445.22
PROBLEM 4C
What rate would you have to earn in order to turn $1MM into $5MM in 10 years? Assume you can invest in a vehicle that compounds monthly.
ANSWER:
FV = PV(1 + i)n
$5MM = $1MM(1 + i / 12)120
5 = (1 + i / 12)120
1.013502 = (1 + i / 12)
i = .013502 per period
i = .013502 × 12 = .162
i = 16.2%
PROBLEM 4D
How long will it take for $1MM to become $2MM? Assume that you can invest in a vehicle that yields 10% on a semiannual 30/360 basis.
ANSWER:
FV = PV(1 + i)n
$2MM = $1MM(1 + .05)n
2 = (1 + .05)n
n = 14.21
Note in this problem the solution from using the exponent keys will be different than the answer from using the PV/FV. This is because using the PV/FV keys on the HP-12C calculates the minimum number of whole periods required to achieve the objective. The exponent keys will work with partial periods. Continue to work through the following problems before moving on to the next section.
PROBLEM 4E
How much would you have to invest today in order to have $1MM in 1 year? Assume that you could earn 12% in an investment that compounds monthly and is quoted on a 30/360 basis.
ANSWER:
PV = FV / [(1 + YTM / PPY)n]
PV = $1MM / [(1 + .12 / 12)12]
PV = $1MM / [(1 + .01)12]
PV = $887,449.23
PROBLEM 4F
How much would you have to invest today in order to have $1MM in 1 year? Assume that you could earn 12% in an investment that compounds daily and is quoted on a 30/360 basis.
ANSWER:
PV = FV / [(1 + YTM / PPY)n]
PV = $1MM / [(1 + .12 / 360)360]
PV = $1MM / [(1 + .00033333)360]
PV = $886,938.28
Assume that you invest $1MM in an investment that yields 10% on a 30/360 calendar and compounds monthly. How long will it take to double your money?
ANSWER:
FV = PV[(1 + YTM / PPY)n]
$2MM = $1MM[(1 + .10 / 12)n]
2 = [(1 + .10 / 12)n]
2 = 1.008333n
83.49
PROBLEM 4H
How much interest will you earn if you invest $1MM on January 12, 1997, until August 27, 1997, at 8%? Assume that the yield is expressed on an A/360 basis and that the investment compounds daily.
ANSWER:
FV = PV[1 + (YTM / PPY)]n
FV = $1MM[1 + (.08 / 360)]227
FV = $1,051,732.49
I = $51,732.49
PROBLEM 4I
You invest $1MM in an investment that yields 10% on an A/360 basis and compounds daily. How much will you have at the end of a year?
FV = PV[1 + (YTM / PPY)]n
FV = $1MM[1 + (.10 / 360)]365
FV = $1,106,691.45
PROBLEM 4J
What is the market value of a $1MM 30-year euro ZCB that’s priced to offer a 12% YTM?
ANSWER:
PV = FV / [1 + (YTM / PPY)]n
PV = $1MM / [1 + .12 / 1]30
PV = $33,377.92
PROBLEM 4K
What is the market value of a $1MM 30-year US corporate ZCB that’s priced to offer a 12% YTM?
ANSWER:
PV = FV / [1 + (YTM / PPY)]n
PV = $1MM / [1 + .12 / 2]60
PV = $30,314.34
PROBLEM 4L
What will $1MM grow to in 1 year when invested in an instrument with a 10% return and the compounding frequencies listed?
FVAN = $1MM (1 + .10)1
FVSA = $1MM (1 + .10 / 2)2
FVQ = $1MM (1 + .10 / 4)4
FVD = $1MM (1 + .10 / 360)360

PROBLEM 4M
What rate will grow $1 to $2 over a 1-year time frame for each of the alternative compounding frequencies listed?
SRAN = FV = PV (1 + r / 1)1
SRSA = FV = PV (1 + r / 2)2
SRQ = FV = PV (1 + r / 4) 4
SRM = FV = PV (1 + r / 12)12
SRD = FV = PV ( 1 + r / 360)360
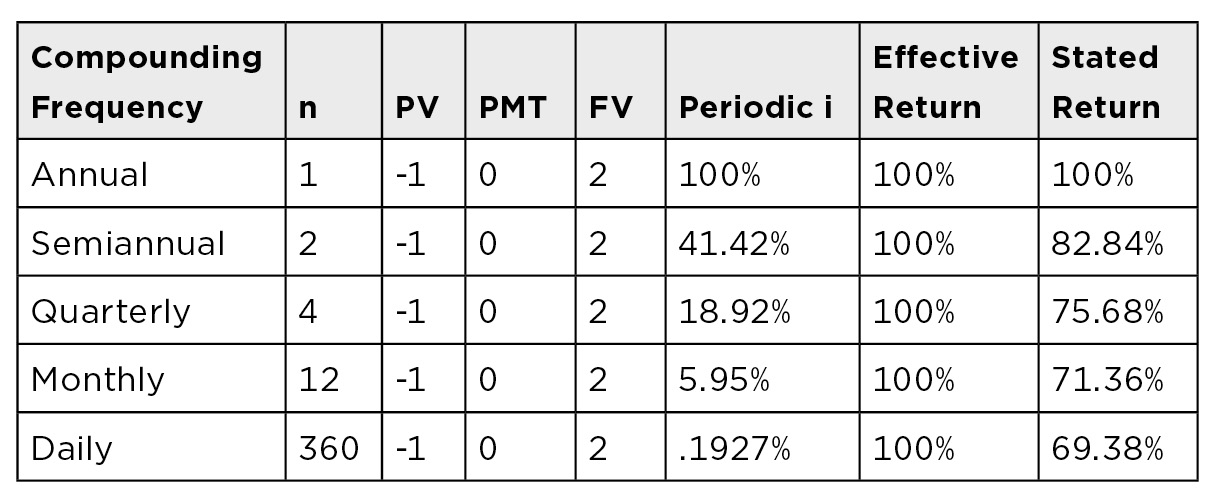
Note that in this problem, in every case, the investment doubles over the course of a year. Effectively, the investor earns a 100% return. The stated returns, however, vary depending upon the compounding frequency. Investments are quoted in the market place based on their stated return.
Stated and Effective Returns
Much of the confusion surrounding the real return of investments that compound stems from the way that the returns of investments are quoted. The returns of investments which compound are typically quoted by their stated returns instead of the effective annual return.
The stated return, as illustrated in Problem 4M, is equal to the interest rate per period simply multiplied by the number of periods per year. It does not take the impact of compounding into account. The effective return is the annual rate that the investor actually earns on the original invested capital—including the impact of compounding. Needless to say, this makes comparative analysis of alternative investment vehicles with very different compounding frequencies a bit complicated. Thus, investments should always be compared on the basis of their effective returns, not their stated returns.
Returns Based on Differing Compounding Frequencies
Most investments have predetermined compounding frequencies. For example, eurobonds compound annually; US Treasuries, US corporates, and US municipals compound semiannually; while mortgages and many collateralized mortgage obligations compound monthly. If there is any doubt about the frequency at which an investment compounds, it is best to note it using the notation in Figure 4.4.
Common Compounding Frequencies
|
Quote |
Interpretation |
|
AN |
Annual rate expressed annually |
|
SA |
Semiannual rate expressed annually |
|
M |
Monthly rate expressed annually |
|
W |
Weekly rate expressed annually |
|
D |
Daily rate expressed annually |
Very often, it is necessary to convert a stated yield based on one calendar conversion to another. To convert a rate expressed on one compounding frequency to its equivalent rate using another compounding frequency, use the formula shown in Figure 4.5. (PPY = payments per year.)
FIGURE 4.5
Rate Conversion

The following examples illustrate the application of this equation to doing rate conversions.
PROBLEM 4N
What rate would a zero coupon investment that compounds monthly have to earn in order to offer the same effective return as a 10% investment that compounds annually?

Enter the stated interest rate (.1) and the periods per year (1) of the known investment, and the periods per year for the conversion (12).


After simplifying the right side of the equation, take the 12th root of each side of the equation. Taking the 12th root of a number is the same as raising it to the 1/12th power. Thus to take the 12th root of 1.1, tap the following keystrokes:
Enter:
1.1 [ENTER]
12 [1/X] [Y><X]

Subtract 1 from both sides of the equation:

Multiply both sides of the equation by 12:
r1 = 9.57%
An alternative way of executing a conversion would be use the PV/FV keys. Alternatively, $1 invested for 1 year in a 10% investment which compounds annually will grow to $1.1. Thus, to convert to a monthly rate using the HP-12C would require:
|
Pay At |
End |
|
n |
12 |
|
i |
? |
|
PV |
-$1 |
|
PMT |
0 |
|
FV |
$1.1 |
|
? × 12 = |
9.57% |
PROBLEM 4O
What rate would a zero coupon investment that compounds daily on a 30/360 basis have to earn in order to offer the same effective return as a 10% investment that compounds semiannually?

r1 = 9.76%
Alternatively, $1 invested for 1 year in a 10% investment that compounds semiannually will grow to become $1.1025.
|
Pay At |
End |
|
n |
2 |
|
I |
5 |
|
PV |
-1 |
|
PMT |
0 |
|
FV |
? |
|
FV |
1.1025 |
Thus, to convert to a daily rate using the HP-12C would require:
|
Pay At |
End |
|
n |
360 |
|
I |
? |
|
PV |
-$1 |
|
PMT |
0 |
|
FV |
$1.1025 |
|
? × 360 = |
9.76% |
PROBLEM 4P
What rate would a zero coupon investment that compounds daily on an A/360 basis have to earn in order to offer the same effective return as a 10% investment that compounds annually?
Since this investment compounds daily and is quoted on an A/360 basis the formula for solving for the rate is:

r1 = 9.40%
Alternatively, $1 invested for 1 year in a 10% investment that compounds annually will grow to $1.1. Thus, to convert to a daily rate expressed annually using the HP-12C would require:
|
Pay At |
End |
|
n |
365 |
|
I |
? |
|
PV |
-$1 |
|
PMT |
0 |
|
FV |
$1.1 |
|
? × 360 = |
9.40 |
Thus, all other factors being equal, the higher the compounding frequency, the higher the effective return. While the previous problems stopped with daily compounding, there is no reason why compounding could not occur every day, every hour, every minute, every second, every nanosecond, and so on. The ultimate limit of this progression is an infinitesimally small compounding period and an infinite number of compounding periods.
Continuous Compounding
Interest rates expressed on a continuously compounded basis have many applications within the world of finance. For example, many option pricing models are based on the concept of continuous rates, and forward rate calculations are much easier when examined on a continuously compounded basis. Financing rates are often quoted on a continuous compounding basis as well.
Continuous rates are dependent upon “base e.” Base e has a value of 2.7183. This number can be calculated one of two ways: The first way, as shown in Figure 4.6, is the limit of the infinite series of 1 divided by the factorials:
FIGURE 4.6
Calculating Base e Using the Limit of the Infinite Series of 1 Divided by the Factorials
e = 1 + 1/1! + 1/2! + 1/3! + 1/4! + 1/5! + 1/6! + etc.
Alternatively, the value of “e” can be determined by compounding $1 at 100% and assuming an infinite number of compounding periods (Figure 4.7)—which is really the same calculation in another form.
FIGURE 4.7
Calculating Base e by Compounding $1 at 100% and Assuming an Infinite Number of Compounding Periods

When the interest rate is compounded continuously, use the formula shown in Figure 4.8 to perform PV/FV calculations.
PV/FV Calculations for Continuously Compounded Interest
FV = PVert
PV = FV/ert
To solve for either the PV or the FV, first multiply the interest rate by the time component. (Remember to use the appropriate calendar convention.) Raise base e to the result by using a hand-held calculator with an ex key or using the =EXP() function in Excel. Then, solve for either FV (given the PV) or the PV (given the FV).
PROBLEM 4Q
You invest $1MM for 1 year at 10% continuously compounded (Cc) on a 30/360 calendar basis. What is the future value?
FV = PVert
FV = $1MMe(.1 × 360 / 360)
FV = $1MM(1.1051709181)
FV = $1,105,170.92
PROBLEM 4R
You invest $10MM on January 15, 1997, for 6 months at 15% Cc on an A/360 basis. What is your future value?
FV = PVert
FV = $10MMe(.15 × 181 / 360)
FV = $10MM(1.078333629)
FV = $10,783,336.29
How much would you have to invest today in order to have $1MM in 9 months? Assume that today is February 15, 1997, and you could earn 12% Cc A/A.
FV = PVert
$1MM = PVe(.12 × 273 / 365)
$1MM = PV(1.0939045206)
PV = $914,156.57
To solve for either the interest rate or the time component it is necessary to take the inverse of base e which requires taking the natural log (ln)—again using a simple calculator. Taking the natural log of base e raised to a power eliminates the e and brings the entire exponent down to the main line, as shown in Figure 4.9.
FIGURE 4.9
Taking the Natural Log of Base e Raised to a Power
ln(ex) = X
PROBLEM 4T
What rate expressed on a Cc 30/360 basis would allow $1MM to grow to $2MM over a 1-year time frame?
FV = PVert
$2MM = $1MMe(r × 360 / 360)
2 = er
ln(2) = ln(er)
.6931 = r
r = 69.31%
How long will it take for $1MM to grow to $3MM? Assume you have invested at 27.67% Cc 30/360 basis.
FV = PVert
$3MM = $1MMe(.2767t)
3 = e.2767t
ln(3) = ln(e.2767t)
1.0986122887 = .2767t
t = 3.97 years
PROBLEM 4V
What rate, expressed on an A/360 basis, is required to grow $1MM to $2MM? Assume that the money is invested from January 1, 1997, to January 1, 2000.
FV = PVert
$2MM = $1MMe(r × 1095 / 360)
2 = e(r × 1095 / 360)
ln(2) = ln(e(r × 1095 / 360))
.6931 = r × 1095 / 360
r = 22.79%