CHAPTER TEN
Variables That Impact Duration
Now that I’ve illustrated how duration is calculated, let’s examine the six main factors that impact a bond’s duration. These include:
- Size of the coupon
- Maturity of the bond
- Yield to maturity
- Tax rate
- Actual payment of interest
- Impact of embedded options
Let’s look at each of these factors in some detail.
SIZE OF THE COUPON
All other factors being equal, the lower the bond’s coupon, the higher its duration. Logically, this makes sense. Lower coupon payments mean less cash flow that can be reinvested at a new rate per year. This extends the time it takes before the ΔIOI can offset the ΔMV.
Consider the following example. Suppose you own two 20-year bonds, one with a 2% coupon and the other with an 18% coupon. Both bonds are priced to offer a 10% YTM. Naturally, the bond with an 18% coupon will be priced at a substantial premium, while the one with a 2% coupon will be priced at a substantial discount.
If market interest rates rise by 1%, the value of both bonds will decline. But, they won’t decline by equal percentages. The low coupon bond declines by 12.85%, while the high coupon bond declines by 7.99%.
MV of 2% 20-year bond priced to offer 10% YTM = $313.64
MV of 2% 20-year bond priced to offer 11% YTM = $277.92 (loss of 12.85%)
MV of 18% 20-year bond priced to offer 10% YTM = $1,696.36
MV of 18% 20-year bond priced to offer 11% YTM = $1,561.61 (loss of 7.99%)
The higher the coupon, the smaller the loss—in percentage terms. In addition, over time, this decline is offset by the increases in the amount of interest on interest that can be earned by reinvesting the coupons at the new 11% rate. In the case of the 2% bond, only $20 per year is received and, therefore, is available to be reinvested. In the case of the 18% bond, $180 per year is received and is, therefore, available to be reinvested at the higher rate.
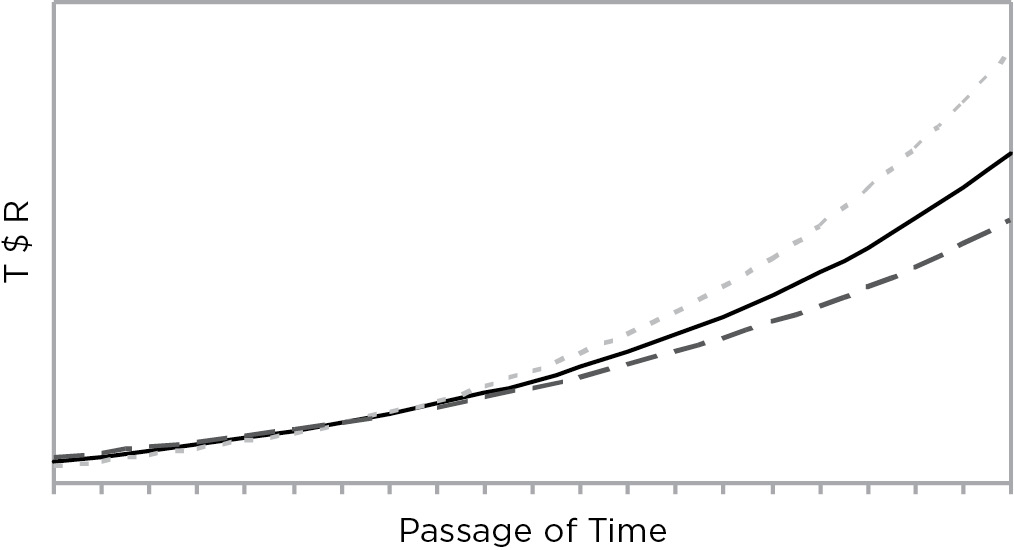
Obviously, it will take less time to offset a 7.99% loss when $180 per year is available for reinvestment at the higher rate than it will take to offset a 12.85% loss when only $20 per year is available for reinvestment. Because the bonds with high coupons can make up a loss so quickly, they are frequently referred to as cushion bonds because investors who own them are cushioned against a rise in rates, as shown in Figure 10.1.
FIGURE 10.1
T$R Curves of High Coupon Bonds
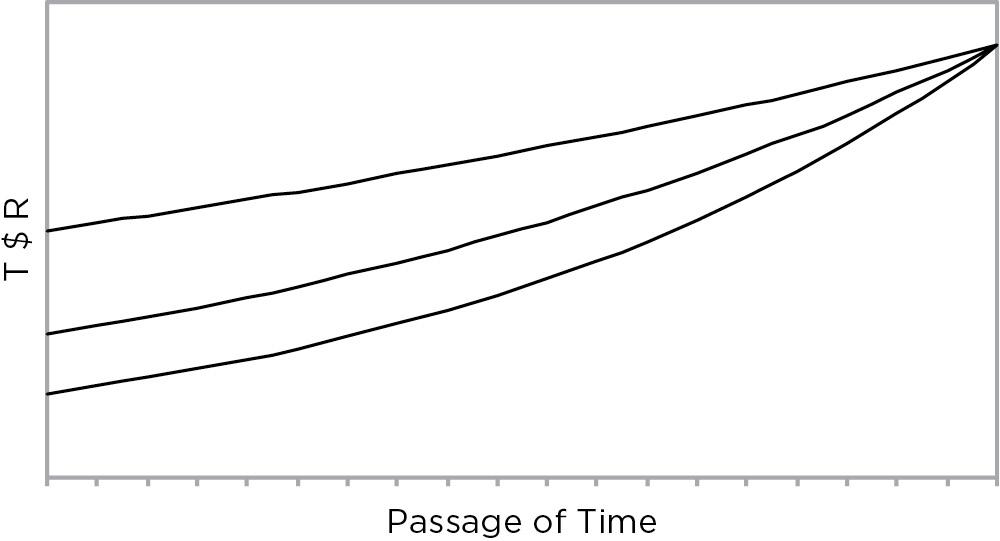
At the other extreme, the duration of zero coupon bonds is equal to their maturity because there is no cash flow to reinvest and there is never a time when the ΔIOI will offset the ΔMV. Figure 10.2 shows the T$R curves for ZCBs.
FIGURE 10.2
Total Dollar Return Curves of Zero Coupon Bonds
The graph shown in Figure 10.3 illustrates how altering the coupon of a 20-year eurobond priced to offer an 8% YTM impacts the bond’s duration. Note that the relationship is not linear.
FIGURE 10.3
Duration of 20-Year Eurobonds with Various Coupons

MATURITY
The second variable that impacts a bond’s duration is its maturity. All other factors being equal, the longer a bond’s maturity, the higher its duration. Remember the numerator in the duration calculation is found by summing the PV of each of the cash flow multiplied by its number. The denominator in the duration calculation is found by summing the PV of each cash flow. Thus, as maturity increases, the numerator increases at a faster rate than the denominator—causing the duration to rise. However, because the number of the cash flow is multiplied by the PV of the cash flows and the present value declines as maturity increases, the duration increases at an ever decreasing rate.
The graph shown in Figure 10.4 illustrates the impact of increasing the maturity of a 10% corporate bond priced at par. As the maturity increases, the duration approaches a limit. Once maturity gets past 40 years or so, the present value of any payments received further in the future is so low that they cause the impact of the payment to be negligible. For this reason, the duration of a 100-year bond is not much higher than that of a 40-year bond.
FIGURE 10.4
Duration vs. Maturity

YIELD TO MATURITY
All other factors being equal, the third variable that impacts duration is the bond’s yield to maturity (YTM). As the bond’s YTM changes, its duration also changes. The reason duration is a function of YTM is that in the duration calculation, the cash flows are present valued by discounting them at the YTM. As the YTM changes, so do the present values of the cash flows and, therefore, so does the duration.
As market interest rates go up, the present value of the bond’s cash flows decline and, therefore, so does the bond’s duration. As market interest rates go down, the present value of the cash flows and, therefore, the bond’s duration declines. The change in the duration of a bond in response to a change in rates is called convexity and it is covered in detail later in this book.
The graph shown in Figure 10.5 illustrates how the duration of a 30-year 10% coupon eurobond is impacted by changing its YTM.
FIGURE 10.5
Duration vs. Yield

TAXES
The fourth variable that impacts a bond’s duration is taxes. Just as is the case with YTM, dealers and newspapers quote duration on a pre-tax basis and leave it to investors to account for the impact of taxes. The tax rate that’s applied to the bond’s interest payments and capital gains or losses is dependent upon both the type of bond and the type of investor. For example, a US corporate bond owned in a pension account would be tax free, while the same bond owned by an individual would be fully taxable.
All other factors being equal, as the effective tax rate on a bond increases, a bond’s duration also increases. An increase in the tax rate increases the bond’s duration because it effectively lowers the amount of cash that can be reinvested. Unfortunately, some investors and fixed income portfolio managers ignore the impact of taxes when they calculate duration.
As the effective tax rate rises, so does the duration of the bond because the cash flow is reduced.
Figure 10.6 shows the impact of taxes on the duration calculation of an 8% 4-year eurobond priced at par. Assume that the investor is subject to a 50% tax rate.
FIGURE 10.6
Impact of Taxes

In the case of zero coupon bonds, when they are held in taxable accounts by investors subject to taxation, the duration actually exceeds the maturity. The reason is that the cash flows in the years prior to maturity are negative because investors have to pay taxes on cash flows they haven’t yet received.
IMPACT oF COUPON PAYMENT
The fifth factor that impacts a bond’s duration is the payment of interest. In between interest payment dates, the duration of a bond decreases in a linear manner. When a bond makes an interest payment, the duration of the bond rises because the short-term cash flow is no longer part of the weighted average. Consider the following example that illustrates the concept. Suppose there’s a bond with three remaining cash flows:
|
0 Years and 1 Day |
$100 |
|
1 Year and 1 Day |
$100 |
|
2 Years and 1 Day |
$100 |
In this case, the weighted average of when the cash flows are received is a year and a day. One day later when the coupon is paid, the remaining cash flows would be:
|
1 Year |
$100 |
|
2 Years |
$100 |
The weighted average is now 1.5 years. Because the short-term cash flow is no longer part of the average, the average is longer. Thus, as the bond approaches maturity, its duration declines in a jagged nonlinear path, as shown in Figure 10.7.
Impact of Interest Payments on Duration

IMPACT oF EMBEDDED OPTIONS
The sixth variable that impacts a bond’s duration is embedded options. A bond that is callable or putable will have a different duration depending upon whether or not the bond is called, put, or survives until maturity. There are two ways to account for embedded options when calculating duration.
The simple, although less accurate, way is to determine whether it is currently attractive to exercise the option. If it is, then assume that the option will be exercised and calculate the duration to the date the option is exercised. If it is not, then calculate the duration to the maturity date.
Consider the following example: Suppose there is a bond that matures in 15 years but is callable in 5 years at a price of $1,030. If the bond is currently selling at a price higher than $1,030, assume the bond will be called, calculate the duration to the call date, and assume that the last cash flow will be $1,030 plus the last interest payment. If the bond is selling for less than $1,030, calculate the duration of the bond to the maturity date.
While that approximate method is certainly easy, it is not especially accurate. Just because the bond is selling above or below $1,030 today doesn’t mean that it will stay there when the bond can actually be called.
The more accurate method is to determine the probability that the bond will be called and the probability that it won’t be called. Then, take the weighted average of the two alternatives to determine the bond’s most probable life. Once the most probable life is determined, the duration can be calculated to this life. This methodology, as well as other aspects of embedded options, is described in the section on option adjusted spreads.
DURATION IS A MOVING TARGET
As you can see, a bond’s duration is a function of coupon maturity, YTM, taxes, and the value of embedded options. Since these all change as time passes, so does a bond’s duration. The bond’s duration point is always a point in the future that you can never reach until the bond matures or is called or put.
Several strategies require matching the duration of a portfolio of bonds to the duration of a pool of liabilities. Because the durations of the assets and liabilities might change at different rates, it is often necessary to rebalance the portfolio to bring the durations back into balance.
DURATION OF ALTERNATIVE DEBT INSTRUMENTS
In the previous sections, calculating the duration of traditional fixed rate notes and bonds was discussed. It is also important to understand how to calculate the duration of nontraditional fixed income instruments. While the calculations are not difficult, it is necessary to think creatively in order to calculate the duration of nontraditional instruments. Examples using floating rate notes, preferred stocks, and interest rate swaps will illustrate.
FLOATING RATE NOTES
Floating rate notes (FRN) are notes with an interest rate that periodically resets to the prevailing market rate as defined by an index. For example, a 5-year FRN might pay US$ LIBOR plus 50 basis points with a 6-month reset. Calculating its duration poses an interesting dilemma because the cash flows are uncertain. There are several alternative methodologies that can be used to calculate the duration of an FRN. The decision of which method to use depends on whether or not the investor expects the FRN to reset at par at its next reset date.
If an assumption is made that the floating rate note has characteristics that will enable it to reset to par on its next reset date, then the note’s duration will equal the time to the next reset date. If the note’s coupon resets in 6 months, the duration of the note is 6 months. One month later the same note’s duration is 5 months. The day before the note resets its duration will be one day, and on the reset day the duration will again be 6 months.
However, if an assumption is made that the note will not reset at par (either because the note’s credit was downgraded or for some other reason), then the duration calculation becomes more complex. Because the note will not reset at par, the only way that the duration of the note can be calculated is to first swap the floating rate cash flows for fixed rate cash flows. The fixed rate cash flows that are the equivalent of the floating rate cash flows can be determined via the swap market. Once the equivalent fixed rate cash flows are determined, the duration of the fixed rate cash flows can be calculated using the traditional duration calculation.
Many investors buy FRNs because they believe that FRNs have very low durations and will lower the durations of their portfolios. Unfortunately, unless the FRNs reset at par, their durations can extend substantially. In this circumstance, instead of shortening the portfolio’s duration, the FRNs increase the portfolio’s duration.
PREFERRED STOCKS
Preferred stocks pose another interesting problem. Equity is perpetual—and therefore a non-putable preferred stock could theoretically pay dividends forever. Because of this infinite stream of future cash flows, it first appears that the duration of a preferred stock is also infinite. Unfortunately, the obvious answer is not always the correct answer.
The reason that the duration of a preferred stock or perpetual bond is not infinite is that each successive cash flow comes further in the future. Since each cash flow comes further in the future, it has a lower present value today. Eventually the cash flows come so far in the future that their present value rounds to less than a penny. Thus, as the maturity of an instrument approached infinity, the duration reaches a limit. Mathematically, this limit is approximately (1 + yield) / yield.
For an 8% perpetual preferred priced at par, the duration would be:
(1 + .08) / .08 = 13.5 years
The same logic applies to perpetual debt offerings, like those occasionally issued by various European sovereign issuers.