CHAPTER SIXTEEN

Active Portfolio Management

Investors who actively manage their portfolios try to outperform the market. They anticipate how the market will change and then position their portfolios to profit from that change. Active portfolio management usually requires additional trading, market data, analytics, and/or personnel, so the active strategy has to generate an extra return that exceeds these additional costs in order to provide real value added. Active strategies fall into two categories: Those that are designed to outperform an index and those that are designed to boost total return without regard to any index. Let’s start with strategies that are designed to outperform an index.

For this section the index we will use is the Barclays Aggregate Taxable Index. This index includes US Treasuries, US agencies, investment grade corporates, and insured mortgage-backed securities. Let’s assume it has the characteristics depicted in Figure 16.1.

FIGURE 16.1

Barclays Aggregate Data

Barclays Aggregate

Weighted average coupon

4.96%

Weighted average maturity

12.22

Weighted average yield

3.96%

Duration

7.61

Modified duration

7.40

Convexity

21

Percent AAA

72%

Percent AA

16%

Percent A

5%

Percent BBB

7%

Percent Treasuries

31%

Percent agencies

14%

Percent corporates

19%

Percent mortgages

36%

There are three ways to outperform an index:

Let’s look at these three alternative methodologies in greater detail.

LIQUIDITY APPROACH

Less liquid securities offer a higher yield than otherwise identical securities that are more liquid. An 8% A rated 20-year bond from a small offering will offer a higher yield than an 8% A rated bond from a $1 billion offering. A $1MM 6% GNMA with a $115K remaining balance will trade at a higher yield than a $1 billion 6% GNMA with an $800MM remaining balance. To the extent an investor can duplicate the index with less liquid securities, the investor can slightly outperform. However, this strategy makes sense only for long-term investors.

FOUR ETF APPROACH

An investor who buys four ETFs that collectively mirror the index can easily make volatility bets by overweighting/underweighting asset classes. Depending on expectations, the investor should use the following courses of action:

THREE ETF APPROACH

In this approach, the investor buys three of the four ETFs—but actively manages the fourth market sector. For example, if the investor has a real expertise in credit analysis, the investor should buy the MBS, AGCY, and UST ETFs and actively manage the corporate bond portfolio. If the investor’s skill allows them to outperform the corporate index and the investor ties the other three sectors, the portfolio as a whole will outperform.

TOTAL RETURN

An investor who is not competing against a benchmark is said to be seeking total return. They can implement all of the strategies we just discussed, as well as a few strategies unique to total return investors. The two most common ones are:

Let’s look at them now.

Riding the Yield Curve

Suppose you want to invest $1MM for 1 year, and you have two choices:

If you expect the yield curve to remain unchanged over the next year, which is a better buy?

FIGURE 16.2

Initial Choice

As shown in Figure 16-3, if the yield curve remains unchanged, then in 1 year:

FIGURE 16.3

After a Year

If the 6% coupon note is sold as a 1-year note offering a 5% return, the net performance of the two notes is as shown in Figure 16.4.

FIGURE 16.4

Relative Performance of Two Notes If Rates Stay Constant

1-Year 5%

2-Year 6%

Buy

5%

6%

Sell

NA

5%

Income

$50

$60

Gain

$0

$9.52

Total

$50

$69.52

The 2-year note earns $69.52, instead of $50.00, which is an incremental return of $19.52 or 39%. Of course, buying the 2-year note and selling it in 1 year is not a risk-free strategy. If interest rates rise, the value of the 2-year note can decline. For example, suppose over the next year interest rates rise by 1%, as shown in Figure 16.5.

FIGURE 16.5

Interest Rates Rise by 1%

In this case, the benefit of riding down the yield curve from 2 years to 1 year is offset by the yield curve rising by 1%, as described in Figure 16.6.

FIGURE 16.6

Relative Performance of Two Notes If Rates Rise by 1%

1-Year 5%

2-Year 6%

Buy

5%

6%

Sell

NA

6%

Income

$50

$60

Gain

$0

$0

Total

$50

$60

If rates rise by 1%, the 2-year note still generates an extra $10—or a 20% incremental return. One-year rates in 1 year would have to rise to almost 7% before the return on the two notes is equal and above 7% before the 1-year note offers a higher return.

The steeper the yield curve, the greater the advantage of riding down the curve. Look at the curves shown in Figure 16.7.

FIGURE 16.7

Two Curves

Figure 16.8 provides details about the pricing of the coupon bonds along both curves.

FIGURE 16.8

Price of Current Coupon Bond Along Both Curves

Start

In 1 Year

In 18 Months

High Curve

9%—$1,000

7%—$1,018.69

5%—$1,019.28

Low Curve

6%—$1,000

5%—$1,009.52

4%—$1,009.71

As time passes, there are two offsetting factors that impact the price of the note. The decline in rates causes the price to rise. The passage of time causes a pull toward par at maturity. If you hold the note too long, the pull toward par exceeds the benefit of rates declining. As a general rule, sell about halfway to maturity. If you buy a 2-year note when the yield curve is steep, sell it in a year. If you buy a 3-year note, sell it in 18 months. Reinvest the proceeds where the curve starts to be steep and reap the profits.

MAKING YIELD CURVE BETS

Yield curve shifts are often nonparallel. Short-term rates can be rising while long-term rates are stable—or even declining. Fed actions that have immediate impact at the short end of the curve may:

Likewise, inflation can cause long-term rates to rise over a multi-year time frame before the Fed chooses to react by raising short-term rates. At the intermediate point of the curve, mortgage activity may heat up—putting pressure on the 10-year point of the curve, without materially impacting the short end or the long end of the curve. For example, suppose an investor expects the Fed to drastically raise short-term rates in an effort to control inflation and, as a result, you expect the yield curve to invert as illustrated in Figure 16.9.

FIGURE 16.9

Current vs. Expected Yield Curve

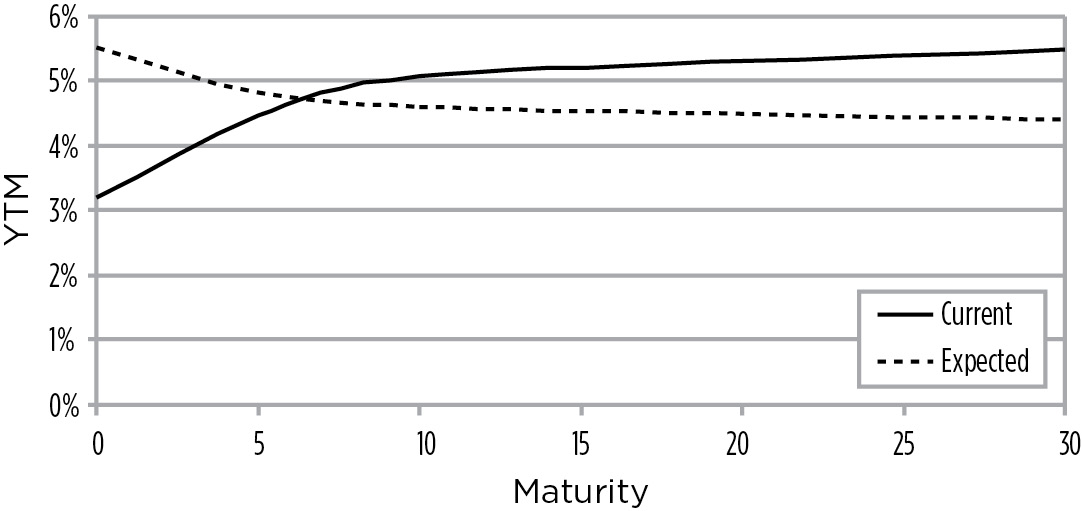
Given this outlook, you might want to go long 20-year euro ZCBs and short 1-year euro ZCBs. Assuming the 20-year ZCBs yields 6% and the 1-year ZCB yields 3%, the value of .01 ΔIR for each would be:

20-year = MV × MD × .0001

20-year = 1,000 / (1.06)20 × (20 / 1.06) × .0001

20-year = $311.80 × 18.87 × .0001

20-year = $0.588

1-year = MV × MD × .0001

1-year = 1,000 / 1.031 × 1 / 1.03 × .0001

1-year = $970.87 × .971 × .0001

1-year = $0.0945

Thus, the ratio of bonds that is necessary to have equal volatility on both sides is 6.24. In this case, you would go short 6.24 1-year ZCBs for each long 20-year ZCB. By having equal volatility, the investor is not exposed to parallel shifts in rates. If rates rise or fall in general, the gain and loss offset each other. This position profits from a yield curve flattening and loses if the yield curve steepens. Assume an investor went short $6.4 MM of 1-year ZCBs and long $1MM of the 20-year ZCBs. If short rates rise 150 basis points and long rates decline 20, the net profit would be approximately:

Short position = 6,400 bonds × 50 × $.0945 = $30,200

Long position = 1,000 bonds × 20 × $.588 = $11,760

There are numerous opportunities to put on yield curve plays during the typical economic cycle, as shown in Figure 16.10.

FIGURE 16.10

Start of the Business Cycle

At the start of the business cycle, the yield curve normally has a positive slope, but it is fairly flat. As the economy heats up, inflation fears enter the economy, and long-term rates start to rise because long-term investors take more inflation risk, as depicted in Figure 16.11.

FIGURE 16.11

Long-Term Rates Rise

When long-term rates start to rise, the Fed tends to react slowly, so long-term and short-term rates start to rise in conjunction with long-term rates. This rise is parallel, as shown in Figure 16.12.

FIGURE 16.12

Parallel Rise

The Fed then gets serious about fighting inflation and raises short-term rates dramatically. This usually causes long-term rates to start declining, as shown in Figure 16.13.

FIGURE 16.13

Fed Dramatically Raises Short-Term Rates

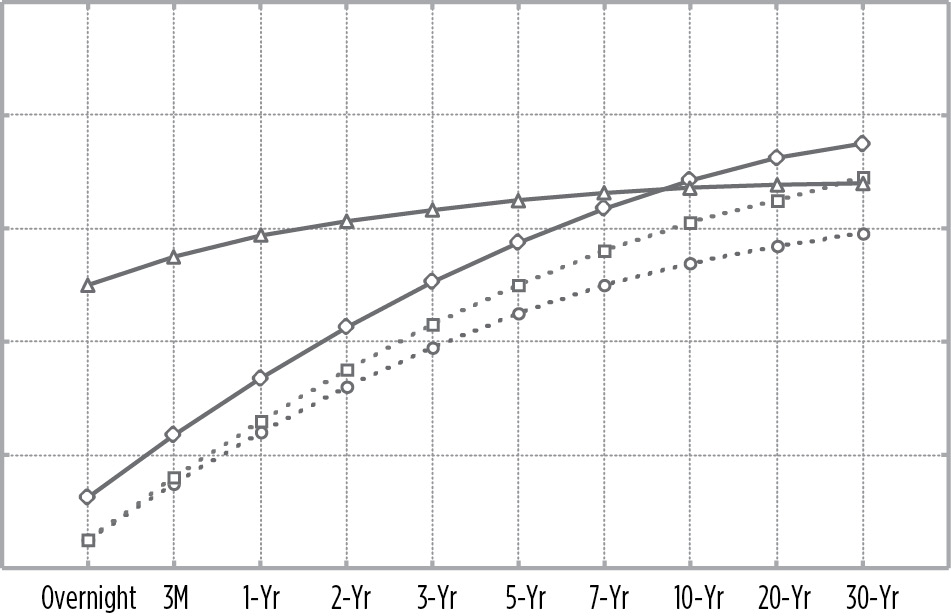
Sometimes the Fed overreacts and raises short-term rates too far, which results in an inverted yield curve. As a result, long-term rates fall faster, as illustrated in Figure 16.14.

FIGURE 16.14

Inverted Yield Curve

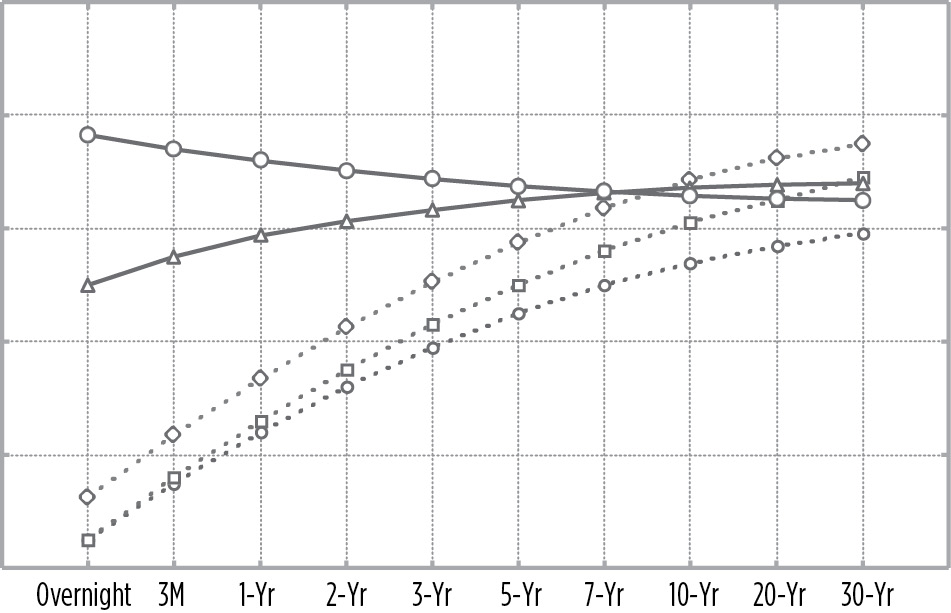
After successfully pushing down long-term rates, the Fed can lower short-term rates (Figure 16.15).

FIGURE 16.15

Fed Lowering Rates After Success

Then the cycle starts over, as illustrated in Figure 16.16.

FIGURE 16.16

The Cycle Repeats

Some additional strategies that are beyond the scope of this text include: