APPENDIX A
Derivation of Modified Duration
The technical definition of modified duration is the first derivative of the price yield function. The term “derivative” means measures the change in. Modified duration measures the change in a bond’s price in response to a change in interest rates. In mathematical notation, the function is sometimes expressed as depicted in Figure A.1.
FIGURE A.1
Modified Duration

While a math background makes understanding derivations a little easier, even those readers without a strong math background should be able to follow the step-by-step derivation offered next. (Understanding the derivation is not necessary for effectively using modified duration).
The market value of any series of future cash flows, such as the series of payments from a bond, is equal to the sum of the present value of the cash flows, where each cash flow is discounted by the periodic yield. The periodic yield, in turn, is equal to the YTM divided by the number of compounding periods per year, as described in the formula shown in Figure A.2.
FIGURE A.2
Periodic Yield Formula
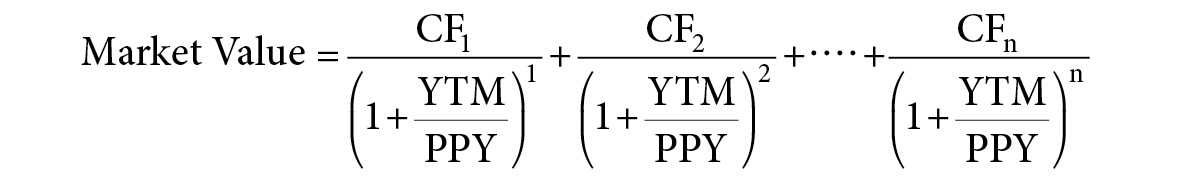
If we take the first derivative of the equation depicted in Figure A.2 with respect to the bond’s yield, the resulting formula would be as shown in Figure A.3.
FIGURE A.3
First Derivative of the Periodic Yield Formula
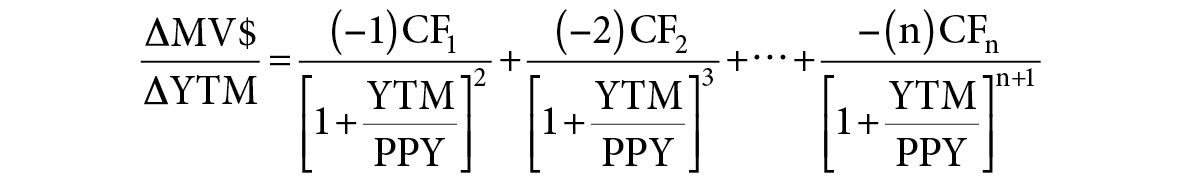
This equation, while correct, is overly complicated. To simplify the equation, factor out the quantity, as shown in Figure A.4.
First Derivative of the Periodic Yield Formula Simplified to Factor Out Quantities

When quantity is factored out of the right side of the equation, the result is as shown in Figure A.5.
FIGURE A.5
First Derivative of the Periodic Yield Formula Further Simplified

The elements of the equation within the large brackets can be restated in a more concise notation that results in the equation shown in Figure A.6.
FIGURE A.6
First Derivative of the Periodic Yield Formula More Concisely Notated
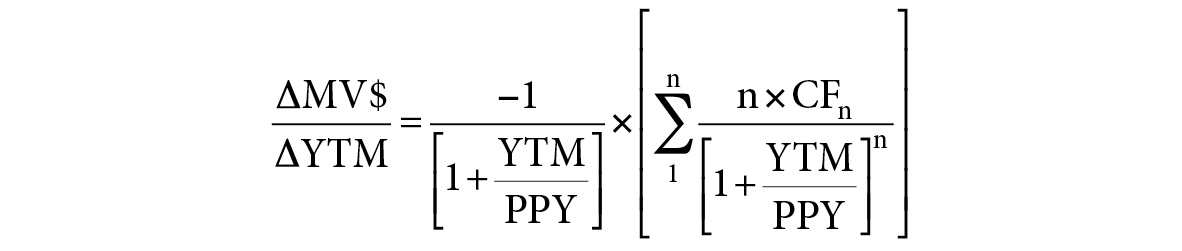
That last equation solves for the change in the market value of a bond (in dollars) for a small change in yield. If you divide the change in the market value (expressed in dollars) by the market value of the bond, the result gives you the change in the value of the bond expressed in percentage terms instead of dollar terms.
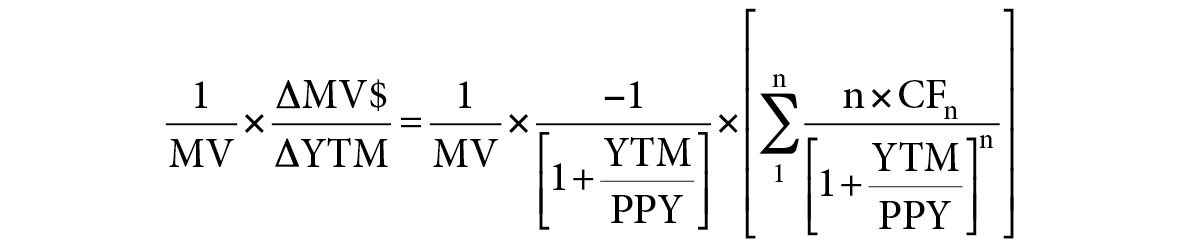
As shown in Figure A.7, to convert the change in price from dollar terms to percentage terms, multiply both sides of the equation by 1/MV—which is the same as dividing both sides by the MV.
FIGURE A.7
Converting the Change in Price from Dollar Terms to Percentage Terms
Which simplifies as shown in Figure A.8.
FIGURE A.8
Simplified Conversion from Dollar Terms to Percentage Terms
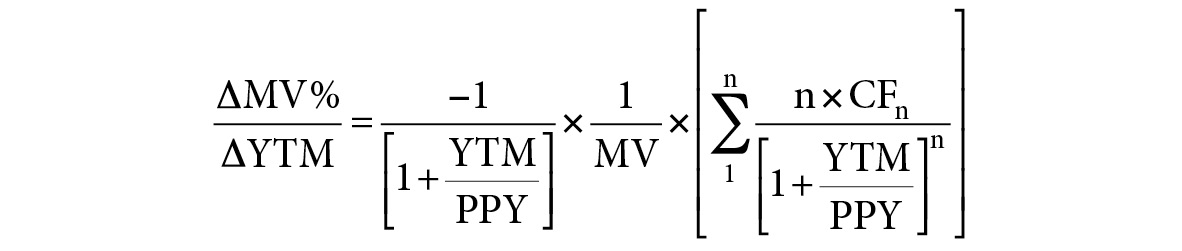
Further simplifying the equation within the brackets leads to the formula shown in Figure A.9.
Further Simplified Conversion from Dollar Terms to Percentage Terms

Multiplying the sum inside the parentheses by 1/MV yields the most common equation for expressing the change in price in percentage terms that results from a change in yield. The equation shown in Figure A.10 is known as the formula for modified duration.
FIGURE A.10
The Modified Duration Formula
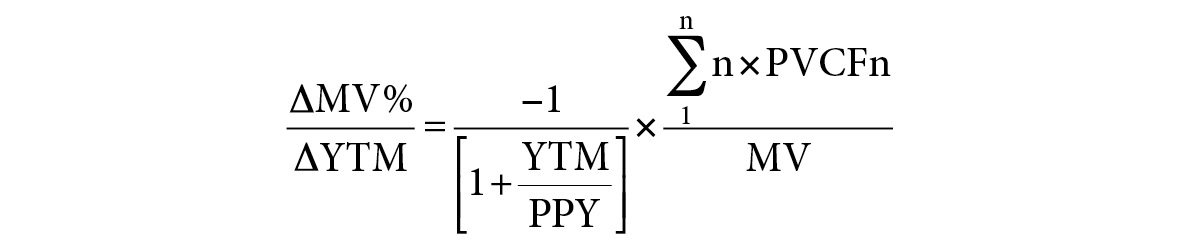
Within the formula for modified duration, as shown in Figure A.11, is the formula for Macaulay’s duration. Macaulay’s duration is the last component of the equation.
FIGURE A.11
The Macaulay’s Duration Formula
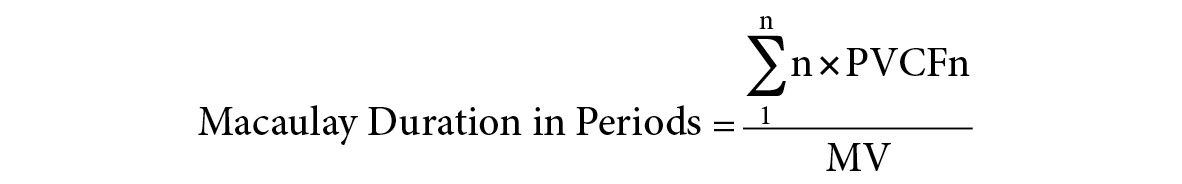
To calculate duration in years instead of in periods, divide the duration in periods by the number of payments per year (PPY). (See Figure A.12.)
The Macaulay’s Duration Expressed in Years

While modified duration measures the change in a bond’s price (in percent) in response to a change in the bond’s yield, Macaulay’s duration measures the point along the bond’s life where the T$RACT equals the T$REXP. Thus, modified duration and Macaulay’s duration are not synonymous, as shown in Figure A.13. Note that the terms are, unfortunately and incorrectly, often used interchangeably.
FIGURE A.13
The Relationship Between Modified Duration and Macaulay’s Duration
