12
Grains in a Fluid
Panta rhei (“All things are flowing”).
Heraclitus
This final chapter will offer the full “fluid perspective” and examine the behavior of more or less compact grain packings in a fluid at rest or in motion. A moving fluid contains a vast variety of immersed granular materials: sediments suspended in a river or a settling pond, sand blown by desert wind, underwater avalanches that can stretch for miles. Readers will call examples of their own to mind as we explore situations illustrating the essential role that fluid flow plays in the motion of grains. The subject of particles suspended in liquid or gas is so vast that it would merit a book of its own. The topic concerns fluid mechanics and the rheology of granular media in equal measure.
A Little Organization!
Grain Concentration
We’ll start with the simplest example, of a unique solid sphere immersed in a flow field. Even when the concentration of particles is low, the flow induced by a grain in the fluid affects other grains. In other words, even though the particles may never touch each other, they nevertheless interact through the fluid. Here, the dominant phase is fluid, but within the grain-fluid mixture—which is known as a suspension—the effect of particles shows up in an increased viscosity of the suspension. In contrast, for high grain concentrations, such as pastes and muds, granular material represents the dominant phase; grain flow is governed by friction between them, as is the case for dry grains. This is why it’s more accurate to speak of immersed granular matter.
Fluid modifies grain flow through viscous forces but also, sometimes, by inertia (as in the case of debris flows). By the same token, fluid can act as an agent of erosion, for instance in rockfill dams or at the bottom of a river. Conversely, it may play a lubricating role—as air does between the grains of a fine powder. Rheology, the science of flows of matter, concerns these materials, which combine grains and liquids.
Grains of Different Sizes
One can discuss the various flow regimes by taking the size and mass of grains as points of reference. Particles that are sufficiently small will remain suspended in the fluid under the effect of thermal agitation (described in chapter 1): the permanent restless motion of small objects as a manifestation of the thermodynamic temperature of a fluid. This constant motion grows in intensity the lower the mass of particles is. Thus, particles spontaneously disperse in space—a phenomenon described by the concepts of molecular diffusion and Brownian motion. Models can be devised where gravity plays no role when the liquid’s density is adjusted to that of solid grains, and in cases where, in a fluid at rest and with very small particles, only molecular diffusion is at work. The density of the liquid can be close to that of the grains: for instance, the salinity of seawater allows us to float without sinking; salted water will also make a fresh egg bob on the surface.
As a rule, gravitation makes particles accumulate as they fall. It counteracts Brownian diffusion, which prompts them to disperse vertically. The result of this conflict is that particles form a layer of sediment at the bottom of the vessel where they are deposited. The higher the particles’ mass is, the more quickly this layer forms. Thermal agitation accounts for small particles spreading in this manner. This is the realm of colloids, where physico-chemical interactions between grains predominate. Take a handful of soil from the yard and empty it into a transparent container filled with water. The large grains will quickly fall to the bottom; the smallest ones, after a certain time, will form dense layers on top of each other. The water that doesn’t clear up entirely is full of tiny particles that remain in suspension.

Figure 12.1
The effect of debris flow in a river torrent in an Alpine mountain range. The lateral dams serve to stabilize the banks.
And what about the largest grains? River torrents can carry blocks of considerable size in debris flows. Mixtures of water, mud, pebbles, and rocks created after heavy rain or in the accidental breaking of dams can cause considerable damage. The lubrication* with a paste made of water, tiny grains, and clayey soils in general makes it possible for heavy rocks to slide over long distances.
The Nature of Fluid
Of course, it’s not the same thing to follow grains that fall in the air, water, or a viscous oil. We’ve named the property of matter—viscosity—that gives rise to a force opposed to the speed at which a small grain moves. If in a fall from one or two meters the speed of a ball increases continuously, it’s because the friction effect of the air limiting the ball’s velocity only proves significant at higher speeds, which are reached only in the course of a longer fall. For grains carried in the air—for instance, the samaras of maple trees that turn like a helicopter blade as they slowly descend, or tufts of dandelions that call a parachute to mind—nature has found strategies for slowing descent by permitting a greater dispersion of seeds under the effect of wind.
Viscosity plays a major role for liquids. Drop a sphere into water—or, better yet, into water whose viscosity has been increased by adding cane syrup—and it will accelerate until friction, which increases with velocity, balances the weight reduced by the effect of buoyancy. For liquids of high viscosity like oil or honey, as well as for objects that are small enough, so-called laminar flows* around a settling particle, described in chapter 11, are regular and predictable. In contrast, if the object in question is sufficiently large and the motion fast enough—say, a sphere one millimeter in diameter falling into water—the fluid flow induced by the fall will present eddies and whirling structures that are unpredictable: this is the domain of turbulent flow.* Recent advances account for the complexity of these flows and their modification, induced by particles whose motion is coupled to that of the fluid.
A Sphere Falls
The Stokes Solution
The motion of a single grain in a fluid provides a necessary precondition for studying suspensions controlled by the effect of viscosity. Yet again, our trusty sphere will lead the way as we watch it fall in a liquid of lower density (figure 12.2). The falling speed V under the effect of weight corrected for buoyancy is vertical. The sphere induces motion in the fluid around and above itself; at the same time, it is slowed down by a frictional force due to the fluid’s viscosity, which increases proportionally to the velocity . The Stokes formula expresses the relation between the velocity V of a sphere of radius R falling in a liquid of viscosity η and the force F (taking into account the Archimedes buoyancy force).
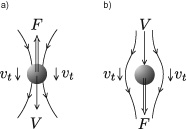
Figure 12.2
a) A sphere falling at a low Reynolds number in a liquid at rest. The force of viscous friction is proportional to the sphere’s velocity . Liquid around the sphere is drawn along at velocity  , which decreases with distance from the sphere. b) A fixed sphere placed in a uniform flow of velocity V experiences a thrust force .
, which decreases with distance from the sphere. b) A fixed sphere placed in a uniform flow of velocity V experiences a thrust force .
Stokes’s law is “robust”: if one doesn’t take the numerical coefficient of proportionality into account, it is the same for objects that have different shapes but the same average size. For a thin rod of length or a flat disc of diameter , the frictional force at a given speed will be close—up to a factor of two or three—to that of a sphere of radius . This fact may seem paradoxical, but there’s an explanation: viscous flows have a long range. If liquid motion is induced at points far from , the whole liquid volume over a distance of the order of is set in motion. Despite the complexity of shapes of all grain types suspended in fluid, at least this represents a simple result. There’s no need to know the exact shape in order to evaluate the order of magnitude of hydrodynamic forces in a dilute suspension.
Fluid Inertia
Drop a sufficiently large sphere into a big vessel filled with liquid, and you’ll see that the sphere oscillates as it falls. This occurs in reaction to swirling motions of the fluid behind the sphere that were not present in the case of laminar flow previously discussed. A turbulent regime now prevails. The friction force is given by ![]() . Force grows as the square of velocity—that is, faster than in a viscous liquid. It no longer depends on viscosity but on the liquid’s density ρ: what counts is the inertia of the liquid brought about by the sphere’s descent. is the cross section of the obstacle seen by flow. The coefficient
. Force grows as the square of velocity—that is, faster than in a viscous liquid. It no longer depends on viscosity but on the liquid’s density ρ: what counts is the inertia of the liquid brought about by the sphere’s descent. is the cross section of the obstacle seen by flow. The coefficient ![]() takes into account the effect of the shape; it is small for elongated shapes with an unimposing profile (like the compact car manufactured by Citroën called “CX”).
takes into account the effect of the shape; it is small for elongated shapes with an unimposing profile (like the compact car manufactured by Citroën called “CX”).
Diffusion and Mobility
We have often referred to disordered motion displayed by “small” grains of matter as the result of thermal agitation. The significance of such movements can be evaluated in the context of sedimentation. Orders of magnitude are easy to remember. A sphere 0.5 μm in diameter and twice as dense as water falls at a speed of 0.5 μm per second. Its velocity due to thermal agitation at ambient temperature is also 0.5 μm per second. On this scale, the movements imposed by external forces and thermal agitation are comparable. The Reynolds number is of the order of one millionth: inertia effects are negligible!
A dimensionless number enabling us to predict whether a particle will display significant Brownian motion under the effects of flow is the Péclet number (Pe).* It replaces the Reynolds number for a flow: the molecular diffusion coefficient replaces the viscosity. The Péclet number compares the effects of flow and molecular diffusion. If it is large, disordered motion due to Brownian collisions proves insignificant relative to flow effects. In the opposite case, thermal agitation prevails.
Interacting Particles
A Sphere in a Tube
Let’s start with the behavior at low Reynolds numbers. What happens when a single particle falls in a tube? The lateral walls reduce the flow induced by the sphere’s motion and slow it down: if the diameter of the cylinder is ten times that of the sphere, the decrease of its velocity will be of the order of 10%. It’s a surprising result: one might think that a sphere would be perfectly at ease in a tube ten times larger! This proves that, at a low Reynolds number, the effects of flow around an object make themselves felt at large distance from the object. Now consider a sphere approaching the bottom of the cylindrical vessel. It’s difficult to get rid of the thin film of liquid between the sphere and the plane because of dominant viscous effects. Lubrication is at work; as noted earlier, it refers to friction between two solid bodies separated by a thin fluid layer. The effects bear on many problems in industry far beyond the scope of the suspensions discussed here and belong to the field of tribology. We have seen the importance of tiny surface irregularities at the interface between grains in the context of dry contacts. In a similar way, the thin liquid film between two objects that are extremely close and approaching each other limits their speed of approach.
Interaction between Two Spheres
When a particle moves, the flow affects its neighbors. The same phenomenon holds for a flock of migrating birds or a pack of cyclists in a race. Beneficial interactions between the leader of the flock or pack and the others behind them are not symmetrical (the latter don’t help the former!); this is characteristic of the high Reynolds numbers. In contrast, low Reynolds numbers entail reciprocal interaction between particles.
A Bundle of Spheres Falling
If one places several spheres side by side in a fluid, the effect of their fluid-mediated interactions will prompt each one of them to fall faster than if it were alone: the bundle moves faster than a single sphere, as if the particles were attached (figure 12.3a). That might seem reasonable, but it is not the case in practice because of the geometry of the container: If the number of particles increases indefinitely, their falling speed—that is, the sedimentation rate—should become extremely high. In practice, however, the velocity for a large ensemble of particles decreases when their density reaches a high enough level!
The reason is the back flow of liquid that the particles have set into motion in the presence of a solid bottom surface of the container, which stops the downward fluid flow. Thus, in a closed tube, the counterflow velocity ![]() slows down the fall of grains (figure 12.3b) and the sedimentation velocity decreases as its concentration grows.
slows down the fall of grains (figure 12.3b) and the sedimentation velocity decreases as its concentration grows.
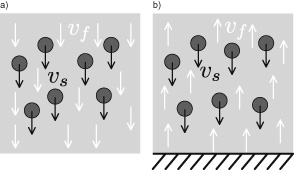
Figure 12.3
a) When a pack of grains sediments, the fluid is pulled downward. Its proper falling speed  is compounded by an additional component
is compounded by an additional component 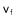 induced by the fall of neighboring grains. b) If the grains are in a closed tube, an upward counter-flow
induced by the fall of neighboring grains. b) If the grains are in a closed tube, an upward counter-flow 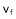 will take place between grains and slow them down; the settling rate diminishes as concentration increases.
will take place between grains and slow them down; the settling rate diminishes as concentration increases.

Figure 12.4
The Boycott effect: a) the length of a settling grain’s trajectory in a vertical tube is greatly shortened in b), when the tube is tilted. The fall of particles and rise of fluid take place in different parts of the tube, leading to much faster sedimentation.
This illustrates the Boycott effect, named in recognition of the doctor who observed that when he tilted the tube in which he was measuring the sedimentation of red globules, the process occurred more rapidly than when the tube remained vertical. The particles descend along the low side of the tube, while the liquid rises along its upper side; the back flow has been channeled and has no effect on the fall of particles (figure 12.4)! The same effect is sought in order to improve foot traffic, when many pedestrians are moving in opposite directions.
Sedimentation
Pour a dilute collection of microscopic grains into a test tube filled with a liquid (figure 12.5). Shake it to homogenize the suspension; then let the grains sediment. The upper part will clarify. The boundary between the clear liquid above it and the homogeneous suspension below falls at velocity vs, which is also the speed at which the individual particles fall throughout the volume. When the initial concentration rises, this velocity declines as a result of viscous friction, as previously discussed; this decrease becomes more and more pronounced as the maximum concentration of spheres (that is, of spheres in contact) is approached.
Particles accumulate at the bottom of the vessel and form a loose pile of grains, a sediment whose thickness grows at a lower speed ![]() , of the opposite sign, as particles get collected.
, of the opposite sign, as particles get collected.
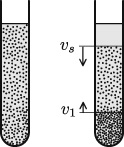
Figure 12.5
In sedimentation starting from a homogeneous suspension at left, identical particles will fall in liquid at an individual velocity 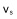 , which is also the velocity of the front holding pure liquid above. In contrast, the upper front of sediment rises at a lower speed
, which is also the velocity of the front holding pure liquid above. In contrast, the upper front of sediment rises at a lower speed 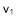 .
.
Sediment Formation
In geological time scales, this process led layers of grains to form sedimentary rocks, which today cover three-quarters of the Earth’s surface. Such rocks bear traces of strata produced by sedimentation and by the effects of flows. Once dried, sediment is generally not very compact; you can confirm as much when walking on the surface of a dried-out lake. Indeed, during deposit formation, the deceleration of particles as a result of the liquid’s viscosity and lubrication effects between grains prevents them from reorganizing themselves enough to reach a high packing fraction.
Chemical Interactions
The packing fraction can be even lower if chemical interactions occur between particles. This is the case for colloidal particles in which tiny grains attach to each other to form a fractal object that calls a snowflake to mind (figure 2.9). In the course of sedimentation, colloidal particles—for instance, those made from clayey mud—collide as a result of thermal agitation and stick to each other. This yields flakes whose settling rate grows with size. The process accelerates until these objects “full of void” come into contact, at which point they form a very weak random continuous lattice—a gel. If a 5% concentration of bentonite clay is placed in water, sedimentation stops when just half the suspension has clarified, but this 5% fills up half the volume!
The importance of physical chemistry can be gauged by observing the viscosity of a suspension of small silica grains; their modest size is responsible for strong attractions between particles. These grains tend to aggregate, which is countered by electrical charges of the same sign at the surface of particles. Varying the acidity—pH—of the solution makes these charges change. Electrophoresis allows this effect to be measured. The mobility of particles is charted as an electrical field is applied. In an acid medium, the silica particles move in the direction of the field, whereas they move in the opposite direction in a basic medium. Between these extremes, an isoelectric point exists, where the effect of charges disappears. The viscosity of suspensions reaches a maximum around this isoelectric pH value because particles no longer repel each other; they form large bundles, thereby increasing viscosity.
Electric charge effects are not the only cause of repulsion that opposes particle aggregation. The science and engineering of colloids is based on treatments for giving grains a surface layer that keeps them separate. Research on polymers has shown how to cover a solid surface with polymer chains. By way of comparison, consider opposite types of hair—tightly curled and perfectly straight, for example—to get an idea of how these microscopic polymers keep grains apart (for instance, the carbon grains suspended in India ink).
Agitated Particles
We have seen particles falling under the effect of their own weight in a liquid at rest and interacting with each other through a flow their motion has induced. How do collections of particles behave in the absence of sedimentation?
The Dance of the Particles
We will start with a situation that permits us to disregard the weight of grains by adjusting the density of the fluid in which they are swimming to that of the grains. Conducting a free space experiment at zero gravity would also work, but that would prove much more costly!
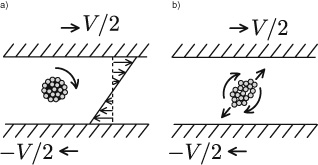
Figure 12.6
a) Placed between two parallel plates moving at opposite speeds, an agglomerate of consolidated spheres rotates at an angular velocity corresponding to the shear rate. b) If the spheres of this agglomerate are free to separate, the bundle stretches out at a 45-degree angle to the flow.
Simple shear, which we discussed in chapter 4 (figure 4.6), represents the most classic kind of flow. We’ll start by putting a single sphere halfway between two plates moving at opposite speeds and separated by the liquid (figure 12.6). The liquid’s velocity in the median plane is zero: instead of moving, the sphere rotates at an angular velocity γ, the shear rate (velocity divided by the distance between plates). This rotation is due to the friction of the liquid, which heads in opposite directions at the top and bottom of the sphere.
In a simple shear flow, this rotation effect is accompanied by an elongation effect: the liquid near the top is drawn to the right, and the liquid near the bottom to the left; in a sense, the liquid is being stretched. Other means exist for obtaining this elongation effect. For example, one can let a liquid flow through a small opening made on the bottom of a receptacle; elongation occurs because of convergence of fluid above the hole.
Let’s consider an array of consolidated spheres in a general flow field. The spheres will turn around their own axes due to the rotational part of the flow field. But in response to the elongation part of the flow, they will change partners by attracting new grains and losing old ones. Here we have the elements of a random ballet whose choreographer is the nature of the flow.
Fluidization
Instead of grains falling in a liquid at rest under the effect of their own weight, imagine particles being held up from below by a jet of liquid or gas—say, a ping-pong ball floating at the top of a spout of water. If the friction the liquid exerts on particles balances the effect of their weight, they will remain suspended. If the speed of the fluid heading upward is high enough, the spheres’ motion will be agitated by turbulent flow. This phenomenon is at the origin of fluidization,* which occurs with flow at a greater speed than with sedimentation.
Figure 12.7 shows a model experiment. An ensemble of identical grains has been placed on top of a grid that is fine enough to hold them, and a fluid is injected from below. As long as upward velocity remains low, the grains behave like a filter set in place, and the fluid passes through it (figure 12.7a). Above a velocity threshold at which the fluid’s thrust balances out the weight of a particle, the bed of grains rises uniformly (figure 12.7b). A stable bed can be obtained at a value just above the fluidization threshold, but this does not prevent the grains from being in a state of constant movement with respect to each other. If the flow velocity is raised again, the particles’ motions will grow erratic. The flow itself becomes turbulent, and bubbles of pure fluid rise through the bed so that two phases are present simultaneously—pure fluid, on one hand, and fluid containing grains, on the other hand (figure 12.7c). Pure fluid is less dense than fluid charged with particles, and the bubbles call to mind a convective phenomenon whereby a liquid that is hot and less dense than the averaage temperature rises up in “thermal plumes.” Such instabilities prove quite important if fluidization involves a gas; because of the large difference in density between solid grains and a fluid, they can impair the functioning of industrial equipment that requires a high level of homogeneity in mixtures.
The fluidized bed may be deemed a new state of matter. Without a form of its own, it is not very dense but consistent. It has many applications in industrial engineering, where the goal is to maintain fine grains of matter in active contact with a fluid. This may involve, for instance, blowing hot air upward to make floating carbon powder react with it—a process that promotes efficient combustion. Indirectly, the effects of atmospheric pollution caused by incomplete combustion are reduced.

Figure 12.7
a) Subjected to an upward fluid flow, if the velocity of the rising fluid is insufficient, the fluid circulates through the porous space between the fixed spheres. At the fluidization threshold speed 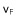 , which is larger and opposite to the speed of sedimentation, the bed rises up since b) the weight of the spheres is overbalanced by friction. c) For higher fluidization velocities, the fluidized bed is unstable because of bubbles of fluid rising through it.
, which is larger and opposite to the speed of sedimentation, the bed rises up since b) the weight of the spheres is overbalanced by friction. c) For higher fluidization velocities, the fluidized bed is unstable because of bubbles of fluid rising through it.
The Viscosity of a Suspension
How Viscosity Varies with Concentration
A simple method for evaluating viscosity η of a pure liquid is to measure the time it takes for a small sphere (at low Re number) to fall in the liquid: this is the principle at work in the so-called falling ball viscometer. Other devices are based on the principle of simple shear, for example the Couette viscometer, which consists of one cylinder rotating inside another fixed cylinder on the same axis. Laminar flows exhibit proportionality between the angular velocity and the applied torque; the suspension’s effective viscosity ![]() represents the ratio between these two quantities.
represents the ratio between these two quantities.
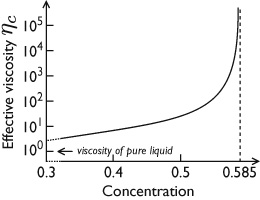
Figure 12.8
The effective viscosity of a suspension as a function of concentration 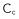 .
.
Figure 12.8, which shows how this quantity increases with the concentration (or packing fraction) of particles ![]() , will guide our dicussion. Viscosity starts from
, will guide our dicussion. Viscosity starts from ![]() —the value for the pure liquid—and increases in a linear fashion because of the viscous friction between grains induced by shearing. This variation becomes more rapid as particle concentration increases and grains get closer. Now, however, the mechanical effects between grains in contact contribute to the process. So long as conventional liquids are employed, and dilute suspensions, the measurement of viscosity yields the same value, no matter what kind of viscometer one uses. This is not the case at high concentrations because the arrangement of grains and, in consequence, energy dissipated as they move about depend on the type of flow at work.
—the value for the pure liquid—and increases in a linear fashion because of the viscous friction between grains induced by shearing. This variation becomes more rapid as particle concentration increases and grains get closer. Now, however, the mechanical effects between grains in contact contribute to the process. So long as conventional liquids are employed, and dilute suspensions, the measurement of viscosity yields the same value, no matter what kind of viscometer one uses. This is not the case at high concentrations because the arrangement of grains and, in consequence, energy dissipated as they move about depend on the type of flow at work.
A Dilute Suspension
Take a suspension with a small percentage of grains. Viscosity will increase because of friction between the fluid and particles. The result is summed up by a formula Einstein developed during his classic work on Brownian motion. The viscosity of a dilute suspension of particles of concentration ![]() equals that of the suspending liquid η multiplied by a coefficient higher than the unity depending linearly on concentration:
equals that of the suspending liquid η multiplied by a coefficient higher than the unity depending linearly on concentration: ![]() ; thus, for a concentration of 4%, viscosity will be higher than that of the pure liquid by 10%. One way of increasing viscosity, then, is to replace pure liquid with a liquid containing solid particles. The remarkable thing about the formula is that the viscosity doesn’t depend on the size or shape of the particles.
; thus, for a concentration of 4%, viscosity will be higher than that of the pure liquid by 10%. One way of increasing viscosity, then, is to replace pure liquid with a liquid containing solid particles. The remarkable thing about the formula is that the viscosity doesn’t depend on the size or shape of the particles.
At High Concentrations
Viscosity increases faster and faster along with the concentration of particles. Eventually, the particles begin to collide and form an increasingly dense network. Forces are transmitted both by the contact network between particles (as in the case of dry granular flow), and by the fluid. Consider a pressure-controlled system like the one in chapter 8 (figure 8.1).
To study suspension shear flow under controlled pressure, a new rheometer was developed at Aix-Marseille University (figure 12.9). In this cylindrical apparatus, the granular packing is immersed in a liquid and confined by a porous cover that can let the liquid pass, and over which a constant confining pressure is applied. Since the liquid can easily pass through, the grains sustain all the pressure. The wall’s rotation around the axis directly shears particles in a continuous fashion. In this way, the rheometer allows researchers to examine the grain assembly’s resistance to shear in the presence of a liquid for different levels of confining pressure and fluid viscosity.
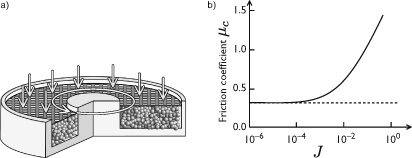
Figure 12.9
a) Rheometer for suspensions at controlled confining pressure: grains immersed in a liquid are confined between two fixed cylinders with a porous cover that lets through liquid (but not grains) as it rotates. Pressure is applied on the cover, and the suspension is sheared by the rotation of the inner cylinder. b) The suspension’s coefficient of friction 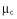 is measured by dividing the shear stress by the pressure applied to the cover. This curve shows how friction varies as a function of the parameter , which is the ratio between the viscous stress the fluid exerts on grains and the confining stress.
is measured by dividing the shear stress by the pressure applied to the cover. This curve shows how friction varies as a function of the parameter , which is the ratio between the viscous stress the fluid exerts on grains and the confining stress.
The rheology of granular flow is characterized by the way the effective friction coefficient ![]() and the concentration
and the concentration ![]() vary as a function of the viscous number . The effect of can be studied from two different points of view:
vary as a function of the viscous number . The effect of can be studied from two different points of view:
- • From the particle viewpoint, the situation corresponds to that of dry flows. In this case, however, the rheology is governed by the viscous number which accounts for the fluid viscosity—instead of the inertial number discussed in chapter 8. When increases (with a decrease of , an increase of γ, or decreasing grain size), friction
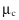 increases and packing fraction
increases and packing fraction 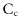 decreases, as shown on figure12.9b. The dense limit (large value of
decreases, as shown on figure12.9b. The dense limit (large value of 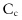 ) corresponds to low values of , that is, to large values of or low viscosity values. This is the quasi-static limit we discussed in chapter 8.
) corresponds to low values of , that is, to large values of or low viscosity values. This is the quasi-static limit we discussed in chapter 8. - • From the liquid viewpoint, the suspension flow is characterized by effective viscosity
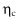 instead of effective friction coefficient
instead of effective friction coefficient  . To measure
. To measure 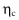 , the distance between mobile plates is fixed, so that the cell volume is constant. In other words, the volume is monitored instead of the confining pressure.
, the distance between mobile plates is fixed, so that the cell volume is constant. In other words, the volume is monitored instead of the confining pressure.
Although the effective viscosity is measured at fixed volume, its value is related to the effective friction coefficient measured at fixed confining pressure. Indeed, given the expressions of the shear stress ![]() in terms of effective viscosity
in terms of effective viscosity ![]() and normal pressure , and the definition of viscous number
and normal pressure , and the definition of viscous number ![]() , it is easy to see that
, it is easy to see that ![]() . This relation allows one to obtain the evolution of
. This relation allows one to obtain the evolution of ![]() with from the evolution of
with from the evolution of ![]() with . It implies that the effective viscosity diverges as tends to zero while at the same time the packing fraction tends to its critical value
with . It implies that the effective viscosity diverges as tends to zero while at the same time the packing fraction tends to its critical value ![]() .
.
As figure 12.8 shows, the rapid increase of effective viscosity and its divergence reflects the transition from a state dominated by the fluid (large values of ) to a state dominated by contacts between particles (low values of . At this latter limit, there is enough jamming that particles cannot move with respect to each other, and they form a solid; the packing gets blocked when a constant volume is imposed on the granular assembly, and its effective viscosity diverges to infinity.
Combined Effects of Viscosity and Inertia
The foregoing analysis omitted inertial effects of both grains and fluid. This corresponds to a viscous regime. When the inertial effects of grains are significant—as is the case for rapid geological flows—the inertial forces of particles must be considered; the inertial number and the viscous number are to be taken into account simultaneously. Numerical simulations at the University of Montpellier have shown that inertial and viscous effects are additive: an inertial flow of dry grains on a slope, for example, resembles a viscous flow of grains immersed in a fluid. To understand this connection better, we should remember that the viscosity of a pure fluid results from the random motion of molecules. When agitated grains are added to a fluid, this new factor keeps on increasing the overall viscosity. However, there’s an important difference between the two situations: the erratic motion of molecules is controlled by temperature, whereas the erratic motion of solid grains is governed by shearing and confining pressure (or the weight of grains).
Fluid Inertia
For all that, granular inertia by itself does not mean that fluid is also in an inertial regime. The latter characteristic is evaluated by means of the Reynolds number, which must be considered alongside the values of and to know whether a flow is naturally turbulent. And there we said it … turbulence, the name for one of the most formidable problems facing physics today! Great advances combining numerical simulation, high-power computers, and experimentation have enabled subtle measurements of turbulent fluctuating velocity fields, which have vastly improved our understanding of unstable flows. In particular, imaging technology following the trajectories of very tiny particles present in the flow (particle image velocimetry, or PIV) makes it possible to obtain a 3D map of a fluid’s flow field. This approach has replaced invasive anemometric technologies.
The mixed flows of grains and fluid examined in this chapter have a low Reynolds number. A high Reynolds number is practically always encountered in the earth sciences: on large scales, the effects of a fluid’s viscosity often prove to be secondary, compared with the effects of inertia.
The motion of small particles in a turbulent flow is present in a wide range of natural phenomena. Because this complex problem involves viscosity, inertia, and friction all at once, homogenization is often used: at an elementary level, particles held in suspension by flow turbulence and collisions between grains are then described in terms of effective viscosity, without a detailed reference to the local properties.
Sandstorms provide an impressive example. A sandstorm is characterized by a large cloud of dust advancing at the level of the soil, like a huge billowing wave. The cloud’s movement derives from the difference in density between the air loaded with grains of sand and the less dense uncharged air in front of it. A gravity current of this kind can be simulated at home by pouring a thick drop of sugar syrup into a glass filled with water. It will spread out all over the bottom of the glass. The same mechanism is at work in underwater turbidity currents, where the flow induced by the sloping seafloor can be large enough to lift up immense rocks and cause a veritable underwater avalanche with dramatic consequences for nearby shores.
These last examples indicate that we have reached the end of the path we set out to travel in this book. At this point, the reins should be handed over to specialists in the various related fields of earth science and technology; ideally, our presentation of the principles of granular media will shine a fuller light on their studies. Looking back a few decades—and considering one of the authors’ previous books on the subject and related works—it’s clear that great advances have been charted since then, and many findings have made their way into a more unified field of scientific endeavor. We are confident, then, that shared efforts to arrive at more complete models of understanding these applications will bear even more fruit in years to come.