Soon after I’d mastered the art of card memorization, I wondered if I could transfer this skill to memorizing long sequences of numbers. Our lives are governed by numbers. Telephone numbers, transport timetables, weights and measures, population statistics, election results, PINs, entry codes and numerical passwords – to name a few. Even if you don’t want to attempt the numerical challenges I encounter during competitions, everything has to be quantified, tallied, reckoned, and made secure – so being able to memorize numbers counts!
Psychologists have determined that, on average, the human brain can retain around only seven to nine pieces of data in its short-term (working) memory. This assessment may be accurate, but it’s certainly not insuperable. Using my memory systems, I’ve shown that it’s possible to memorize far more than nine digits (in fact, I’ve memorized well into the hundreds!) at a time, as long as you have a strategy for doing it.
Some people, mathematicians mostly, see real beauty in numbers. I’m sad to say that as I was growing up I wasn’t one of these enlightened folk. Until I started to perform feats of memorization, sequences of numbers to me seemed unintelligible and instantly forgettable. However, now when I look at a series of numbers, they appear completely differently to me. They come to life; they are animated, colourful and even at times humorous. Now, numbers have characters all of their own. Why? Because I have developed a way to convert them from (to me at least) their normal, dull, meaningless form into something that my brain can work with.
The secret to memorizing numbers is to attach significance to them by translating them into coded images. This lies at the heart of a strategy I call my “language of numbers”.
However, there are several simpler systems that people use, so I want to start by teaching you these. For short number sequences, such as memorizing a PIN, they come in pretty handy.
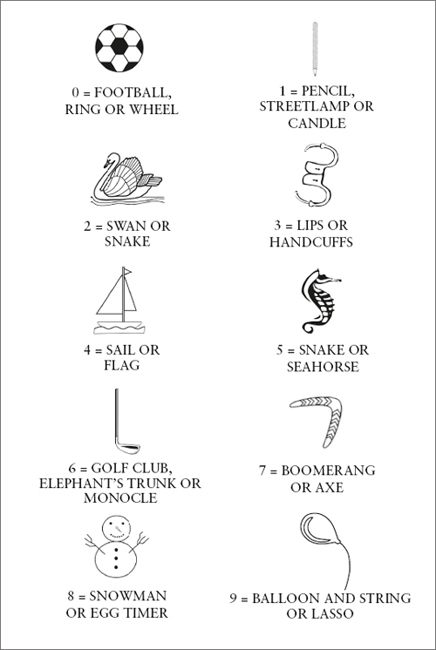
Have you ever looked at the shape of the number “2” and thought that it resembles a swan? Or at “4” and seen the sail of a boat or perhaps a flag on a pole? The number–shape system works on the principle that we can translate any number into an image according to its unique from. As a quick experiment, using a pen and paper, write down the first image that enters your mind as you think of each number form zero to nine. Write down the numbers first, if it helps you. Compare your ideas with mine, which appear in the box on the opposite page (but remember that your own associations will always be stronger for you). I’ve included drawings of some of the associations to make it clearer how the system works.
As there are only ten digits to translate to images, this is a very simple code to learn. Once you’re able to see a number as an object, you can use the object codes to memorize short sequences of numbers by using the objects as elements of a story.
For example, take the number 1 7 9 2, which was the number of steps in the Eiffel Tower when it first opened. Using my number– shape associations, you might picture yourself in Paris at night time, holding a candle (the number–shape for one). Carrying the candle, you head toward the Eiffel Tower. At the entrance you notice a man chopping away at one of the steel legs, using an axe (the number–shape for seven). The futility of this activity makes it all the more memorable. You begin your ascent of the tower steps. When you reach the top, someone hands you a balloon on a string (the number–shape for nine). Give the balloon a colour to make it more memorable – mine is red. As you gaze across Paris, the full moon glows in the night sky and you see the silhouette of a swan – which gives you your number–shape for two – fly across the moon’s face.
Anchoring your story to a location that’s relevant to the number you’re trying to remember is another important aide-mémoire. If you needed to remember your credit card or debit account PIN, a short route around your local bank or from your house to the bank would be perfect.
If number–shapes don’t appeal to you, you could try number– rhymes. This time the image you form to represent the number rhymes with the number sound. So, for one you could have bun, for two, shoe, and so on. Again, create the rhymes that are most natural to you, but I imagine they’ll be quite similar to mine:
0 = HERO, NERO (THE ROMAN EMPEROR)
1 = BUN, SUN
2 = SHOE, GLUE
3 = TREE, SEA
4 = DOOR, BOAR
5 = HIVE, CHIVE
6 = STICKS, BRICKS
7 = HEAVEN (OR PERHAPS KEVIN, IF YOU’VE GOT A FRIEND WITH THAT NAME)
8 = GATE, WEIGHT
9 = WINE, PINE
Let’s say you’re visiting a friend without your car. Your friend tells you that you need to catch the number 839 bus, which stops right outside her house. How could you use the number–rhyme system to remember which bus to catch? Imagine that the bus pulls up at the bus stop. To get on it, you have to open a gate (eight). The first person you see on the bus, sitting in the front row of seats, is holding a small tree (three) in a tub on her lap, as you pass her you notice that the tree is a pine (nine) – perhaps it has Christmas decorations on it to make the pine-tree image more vivid. If you review the scene a couple of times, you won’t forget which bus you’re supposed to be on.
Quick, easy and practical for short sequences of numbers, number–shapes and number–rhymes find their way into my everyday memorizations all the time. However, these systems are not developed enough to help me in World Memory Championships, so I’ve had to devise my own.
Creighton Carvello, who had inspired me to memorize cards in the first place, had managed to memorize pi (the area of a circle, divided by the square of its radius) to 20,013 decimal places. Pi is an infinite number which, as far as we know, doesn’t repeat itself. Consequently, it makes for an excellent measure of a person’s memory capacity. It won’t surprise you to know then, that pi was the next challenge I set for myself.
Over the years, my experimentation with memory techniques has taught me several things about the best way to make information stick, one of them being that letters are easier to turn into usable codes than numbers.
In the early days of my experimentation, I set about coding numbers in exactly the same way as I had coded playing cards: by turning them into letters and then into images. I developed a system for memorizing groups of five numbers, each as a single image. So how does this work for memorizing the decimal places of pi? The first 30 decimal places of pi look like this:
[3.]141592653589793238462643383279
As I studied the first 15 digits, I decided to give each number a specific letter, and to use the letters to form a word or words that I could string into a story. To improve my chances of being able to create a usable sequence of letters, I wrote out the alphabet to U and assigned each number two possible letter codes by running out one to nine twice and then giving 0 the options of S, T and U.
The whole thing looked like this:
| A | B | C | D | E | F | G | H | I |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| J | K | L | M | N | O | P | Q | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| R | S | T | U | |||||
| 9 | 0 | 0 | 0 |
So, 1 = A, the first letter of the alphabet, but also J, which is the tenth letter of the alphabet; 2 = B or K; and so on.
Using these number–letter codes 14159 became AMANI, 26535 translated became BONCE, and 89793 translated became HIPIL. If a particular word didn’t make sense, then I would break the word down into smaller syllables and therefore more images. For AMANI, I imagined an Indian man (a man I); for BONCE, I imagined a head (bonce being a colloquial word for head, of course), and for HIPIL I pictured a hip with a disease: a hip ill. So far so good, until I looked at the next 15 digits complete with their codes:
| 23846 | 26433 | 83279 |
| BLQDO | BOMCC | QCBPI |
These letter sets required quite a bit of creative thinking before I could form some sort of image. So, BLQDO became a block of wood (BLQ) balanced on my own head (DO = Dominic); BOMCC became a bomb (BOM) on a motorbike (CC, as in the engine power of a motorbike) and QCBPI became a barrister (QC) handing a BP (British Petroleum) sign to an Indian man (I). (The images were complicated to come up with, but the best I could think of at the time.)
To remember the numbers in sequence, I created an extended journey from my house leading through the village, the church and its graveyard, over a hill and then into town. I attached the images of each set of five numbers to a stage in the journey, until (with some persistence) I’d laid down a route of 820 stages in a continuous, unbroken journey, each stage representing five numbers of pi. The result was that I could recite pi to 4,100 decimal places.
This was still a long way off Carvello’s record, but I could see that, if I persevered, his achievement would be within reach. However, as a task, converting and memorizing pi proved so arduous that I decided to abandon the project and instead worked on refining the number system itself.
I wanted a system that would allow me to look at numbers and form images almost instantaneously, as if I were reading sentences from a book.
The approach of creating images had worked with playing cards, so why not with numbers, too? And then I realized where my number memorizations had so far been going wrong. Groups of five numbers were too complicated – instead, I should be grouping the numbers into only pairs. As it turned out, as frustrating as learning those few thousand places of pi had been, I’d paved the way for a system that eventually was to help me secure eight World Memory Championships titles – I called it the “Dominic System”.
On reflection, it’s tempting to think my dalliance with pi had been a complete waste of time. However, although I had lost a couple of weeks memorizing all those numbers, I had gained much from the experience. I realized that there really was no limit to what and how much I could remember, as long as I could find enough places in the world to use as mental storage space. I also learned that the speed with which I could memorize those numbers depended upon the efficiency of the system I used and how much I practised using it.