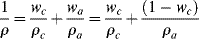Chapter 4
Polymer Morphology
It was pointed out in the previous chapter that the geometric arrangement of the atoms in polymer chains can exert a significant influence on the properties of the bulk polymer. To appreciate why this is so, the subject of polymer morphology, the structural arrangement of the chains in the polymer, is introduced here.
Covalent bonds hold the polymer together but with macromolecules (another term for polymers), the long-range structure is more like a bowl of spaghetti (Figure 4.1), where the backbones of linear polymers twist and turn in a random fashion. This means that the “length” of a polymer is never the actual distance between the end groups in a stretched-out polymer. The dimensional space occupied by a polymer is best described by two parameters, the end-to-end distance, <r>, and the radius of gyration <rg>. Here, the < > brackets indicate that the terms are statistical averages over many polymer chains. <rg> is the average distance from the centroid (mass-weighted center) of a polymer chain to each of the monomer units. It would be equal to the radius of a sphere if a polymer were ever balled up perfectly. Even though that is unlikely, <rg> is a useful term to represent the three-dimensional space taken up by a polymer molecule.
Figure 4.1 Depiction of (a) Three polymer chains randomly oriented and (b) a depiction of the end-to-end distance, <r>, for a single polymer. Also shown in figure (b) is the radius of gyration, <rg>, which represents the average distance from the center of gravity to each monomer unit.
The end-to-end distance is a physical length separating the first and the last repeat units on a single polymer chain. This can have two extremes: on one hand, the polymer can be stretched out entirely along the backbone, limited by bond lengths and bond angles (highly unlikely), while on the other, the polymer can twist and turn and end up with the first and the last repeat unit in the same location (r = 0). When statistically averaged, <r>, is somewhat more useful, as it can indicate whether a polymeric material consists of entwined stretched-out fibers with many weak intermolecular bonds, or if the material is made up of distinct blobs of polymers that prefer weak intramolecular bonds.
The arrangement of individual polymers in a material is broken down to general regions: amorphous (unstructured) and crystalline. This chapter covers the types of crystallinity in polymers and describes how crystals (and the degree of crystallinity) impact the optical and the mechanical properties of the polymers.
4.1 Amorphous and Crystalline Polymers
What is a crystal? For salts and metals, crystals are fairly straightforward because these materials exist primarily as crystals when solid. The arrangement of atoms can affect the type of crystallinity (e.g., face-centered cubic), but the main effect of crystals is to bring atoms together in a regular arrangement. Thinking back to the bowl of cooked spaghetti representation of polymers, regular arrangement may seem nearly impossible (and it is for some polymers, particularly those with bulky side groups). For polymers with small side groups (such as polyethylene), large segments of polymers can arrange into crystals, but there are no polymers that are 100% crystalline.
Although the precise nature of crystallinity in polymers is still under investigation, a number of facts have long been known about the requirements for polymer crystallinity. First, an ordered, regular chain structure (such as an isotactic or a syndiotactic isomer) is necessary to allow the chains to pack into an ordered, regular, three-dimensional crystal lattice. Thus, stereoregular polymers are more likely to have sizable crystalline portions than those that have irregular chain structures. Similarly, large pendent groups, particularly if they are spaced irregularly, hinder crystallinity. Second, no matter how regular the chains, the secondary forces holding the chains together in the crystal lattice must be strong enough to overcome the disordering effect of thermal energy; so hydrogen bonding or strong dipole interactions promote crystallinity and, other things being equal, raise the crystalline melting temperature.
X-ray diffraction studies show that there are numerous polymers that do not meet the above criteria and show no traces of crystallinity, that is, they are completely amorphous. In contrast to the regular, ordered arrangement in a crystal lattice, the chains in an amorphous polymer mass assume a more-or-less random, twisted, entangled, “balled-up” configuration, as in the bowl of cooked spaghetti. A better analogy, in view of the constant thermal motion of the chain segments, is a bowl of wriggling worms. The latter analogy forms the basis of a currently popular quantitative model of polymer behavior known as reptation theory (named for the motion of reptiles).
At the other extreme, despite intensive efforts, no one has succeeded in producing a completely crystalline polymer. The crystalline content may in certain cases (in very regular polymers without bulky side groups) reach 98%, but at least a few percent noncrystalline material always remains. In the case of metals, crystal defect concentrations are normally on the order of parts per million, so metals are generally considered perfectly crystalline in comparison with even the most highly crystalline polymers. Interestingly, recently developed amorphous metals have expanded the range of material properties that can be achieved by many metals. While crystal defects in metals are often the sites of fracture, polymers have covalent bonds linking the crystalline and amorphous regions, making the interfaces between these regions more continuous. The ability to tailor and adjust crystal size and degree of crystallinity (percent crystalline versus percent amorphous) allows for a wide range of mechanical properties in polymers, from rubbery and flexible (largely amorphous with small crystals) to rigid and strong (largely crystalline).
References 1–5 contain extensive discussions of the techniques used to study crystallinity in polymers as well as reviews of research results.
4.2 The Effect of Polymer Structure, Temperature, and Solvent on Crystallinity
Polymer crystals are highly ordered arrangements of polymer segments. Because they are stabilized by weak bonds, anything that can alter or disrupt these bonds will cause a drop in the degree of crystallinity. Perhaps most straightforward is the effect of temperature. As with all crystalline solids, as the temperature rises, bonds holding a crystal together begin to come apart, resulting in a melting transition (Tm). For polymers, it should be noted that only the crystalline portion melts, so a 100% amorphous polymer will not exhibit a Tm (but it will degrade as the temperature continues to rise). The effect of temperature on polymer structure is of great significance, therefore Chapter 6 is devoted entirely to this subject.
Solvents can also disrupt weak polymer bonds, thus they have an effect on crystals similar to melting. Solvents are small molecules (at least when compared to polymers) that can diffuse into a polymer and form new weak bonds, thus replacing polymer–polymer interactions with polymer–solvent interactions. Because polymers are so large, the solvation process can be lengthy (hours to days to dissolve in some cases). In a good solvent, especially in dilute solutions, polymer crystallinity disappears. Upon drying (or cooling a molten polymer), the chains can reform crystals with the crystal size and the degree of crystallinity dependent on the rate of solvent evaporation (or rate of cooling). The behavior of polymers in solution is covered in Chapter 7.
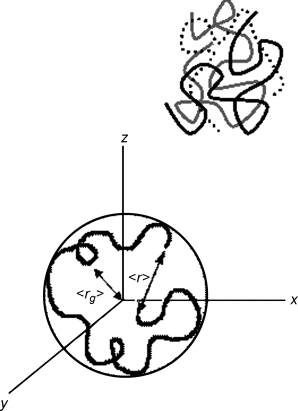
Because polymer crystals have a regular arrangement of the polymer backbone, the side groups (and their tacticity) are crucial in determining whether a polymer will crystallize. Bulky side groups (large groups that extend from the backbone) prevent this alignment, so polymers such as poly(methyl methacrylate), shown below, are entirely amorphous. It should be noted that most polymers do not display appreciable crystallinity, particularly those with bulky side groups that prevent chain alignment. The irregular arrangement of these groups (in atactic polymers) also hinders the formation of crystals. On the other hand, side groups with organic functionalities that can form weak bonds (e.g., –OH) can increase the tendency for a polymer to crystallize.
4.3 The Effect of Crystallinity on Polymer Density
For simplicity, let us assume that only crystalline and amorphous phases are present. With a given polymer, the properties of each phase remain the same but the relative amounts of the phases can vary, and this can strongly influence the bulk properties, particularly the mechanical properties. This is illustrated for polyethylene below, the most crystallizable polymer due to its simple repeat unit structure (–CH2–CH2–).
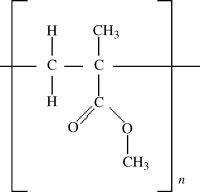
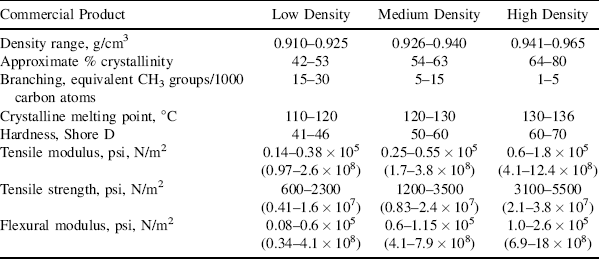
Since polymer chains are packed together more efficiently and tightly in crystalline areas than in amorphous areas, crystallites will have a higher density. Thus, low-density (0.92 g/cm3) polyethylene is estimated to be about 43% crystalline, while high density (0.97 g/cm3) polyethylene is about 76% crystalline. Density is, in fact, a convenient measure of the degree of crystallinity. Because the volumes of the crystalline and amorphous phases are additive, density and degree of crystallinity are related by
where the w's are weight fractions and the subscripts c and a refer to the crystalline and amorphous phases, respectively.
In the case of polyethylene, the differences in degree of crystallinity arise largely from branching that occurs during polymerization (although it is also influenced by the molecular weight and the rate of cooling, as will be discussed later in Chapter 6). The branch points sterically hinder packing into a crystal lattice in their immediate vicinity, and thus lower the degree of crystallinity.
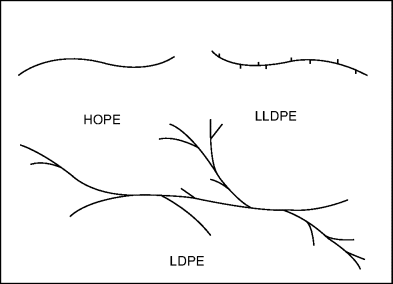
Low-density polyethylene (LDPE) has traditionally been made by a high-pressure process (25,000–50,000 psi) and high-density polyethylene (HDPE) by a low-pressure process (~100 psi). Thus, LDPE is sometimes referred to as high-pressure polyethylene and HDPE as low-pressure polyethylene. If they were not confusing enough, LDPE are now also made by low-pressure processes similar to those used for HDPE. There are also polyethylenes with small grafted organic groups along the backbone. These materials have most unfortunately (and inaccurately) been termed linear, low-density polyethylene (LLDPE). If they were truly linear, they would not be of low density.
Traditional (high pressure) LDPE is a homopolymer. Its long, “branched branches” arise from a side reaction during polymerization. LLDPE, however, has short branches that are introduced by random copolymerization with minor amounts (say 8–10%) of one or more α-olefins (vinyl monomers with hydrocarbon X groups, such as 1-butene, 1-hexene, 1-octene, and 4-methyl-1-pentene). This same approach is extended (by adding more comonomer) to make very-low density polyethylene (VLDPE) or ultralow density polyethylene (ULDPE). (ρ < 0.915 g/cm3). The nature of the branching affects some properties to a certain extent. For example, LLDPEs form stronger, tougher films than LDPEs of equivalent density. The various polyethylenes are summarized in Table 4.1 and their molecular architectures are sketched in Figure 4.2. Equation (4.1) must be used with caution where the density is varied with a comonomer, as in LLDPE, because ρa will, in general, vary with copolymer composition.
Table 4.1 The Influence of Crystallinity on Some of the Properties of Polyethylenea
a. It must be kept in mind that mechanical properties are influenced by factors other than the degree of crystallinity (molecular weight, in particular).
Figure 4.2 Molecular architecture of various polyethylenes.
4.4 The Effect of Crystallinity on Mechanical Properties
Since the polymer chains are more closely packed in the crystalline areas than in the amorphous, there are more of them available per unit area to support a stress. Also, since they are in close and regular contact over relatively long distances in the crystallites, the secondary forces holding them together are cumulatively greater than in the amorphous regions. Thus, crystallinity can significantly increase the strength and rigidity of a polymer. For this reason, stereoregular polypropylenes, which can and do crystallize, are fairly hard, rigid plastics, while irregular, atactic polypropylenes are amorphous, soft, and sticky. And, other things being equal, the greater the ratio of crystalline to amorphous phase, the stronger, harder, more rigid, and less easily deformable the polymer will be, as illustrated in Table 4.1 for the hardness, tensile modulus, tensile strength, and flexural modulus. These parameters (and several others) will be discussed in detail in Chapter 16, but each of these parameters tends higher with an increase in the crystallinity of polyethylene.
4.5 The Effect of Crystallinity on Optical Properties
The optical properties of polymers are largely influenced by crystallinity. A polymer with no additives is normally either clear or white and opaque (or transluscent, somewhere in-between the two extremes), as illustrated in Figure 4.3. When light passes between two phases with different refractive indices, some of it is scattered at the interface if the dimensions of the discontinuities are comparable to or greater than the wavelength of visible light (400–700 nm). Thus, a block of ice is transparent, but snow appears white because light passes alternately from air to ice crystals many times. Similarly, in a crystalline polymer, the usually denser crystalline areas have a higher refractive index than the amorphous areas, so crystalline polymers are either opaque or translucent because light is scattered as it passes from one phase to the other. So, in general, transparent polymer's are completely amorphous, and a simple visual inspection can give clues about a polymer's crystallinity (although additives are often used that can change the optical properties). An interesting exception arises in the case of isotactic poly(4-methyl-1-pentene). The refractive indices (and densities) of the amorphous and crystalline phases are almost identical. Thus, as far as light is concerned, it is a homogeneous material and is the single transparent polymer that is known to be highly crystalline. Also, as the dimensions of the dispersed-phase particles become smaller than the wavelength of visible light (consider nanoparticle additives), scattering decreases, so a polymer with very small crystals and a low degree of crystallinity might appear nearly transparent, particularly in thin sections.
Figure 4.3 Typical plastic objects that are transparent, translucent, and opaque.

The converse is not necessarily true; lack of transparency in a polymer may be due to crystallinity, but it can be caused by an added second phase, such as a filler. If the polymer is known to be a pure homopolymer, however, translucency is a sure sign of crystallinity. Thus, commercial homopolymers of styrene, which is atactic and, therefore, completely amorphous because of the irregular arrangement of the bulky phenyl side groups, is perfectly transparent. Ironically, it is often called “crystal” polystyrene because of its crystal clarity. Isotactic polystyrene has been synthesized in the laboratory and does crystallize. It has the white, translucent appearance typical of polyethylene. Foamed polystyrene (cups, packing peanuts) is white because light passes between atactic polystyrene and gas bubbles. High-impact polystyrene consists of a dispersion of 1–10 μm polybutadiene rubber particles in a continuous phase of atactic polystyrene. Thus, while each phase is completely amorphous and individually transparent, they have different refractive indices, so the composite material scatters light and appears white and translucent.
4.6 Models for the Crystalline Structure of Polymers
4.6.1 Fringed Micelle Model
The first attempt to explain the observed properties of crystalline (the word should be prefaced by “semi-” but rarely is) polymers was the fringed micelle model (Figure 4.4). This model pictures crystalline regions known as fringed micelles or crystallites interspersed in an amorphous matrix. The crystallites, whose dimensions are in the order of tens of nanometers, are small volumes in which portions of the chains are regularly aligned parallel to one another, tightly packed into a crystal lattice. The individual chains, however, are many times longer than the dimensions of a crystallite, so they pass from one crystallite to another through amorphous areas.
Figure 4.4 The fringed micelle model: (a) unoriented; (b) chains oriented by applied stress.
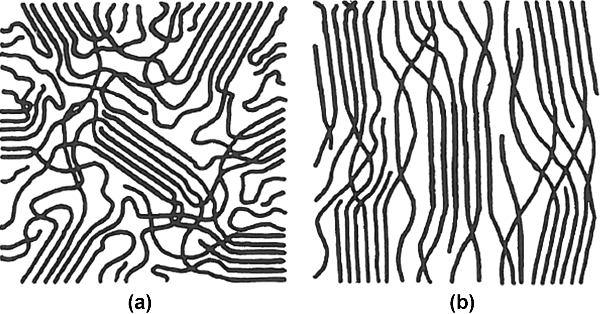
This model nicely explains the coexistence of crystalline and amorphous material in polymers, and also explains the increase in crystallinity that is observed when fibers are drawn (stretched). Stretching the polymer orients the chains in the direction of the stress, increasing the alignment in the amorphous areas and producing greater degrees of crystallinity (Figure 4.4b). Since the chains pass randomly from one crystallite to another, it is easy to know why perfect crystallinity can never be achieved. This also explains why the effects of crystallinity on properties are in many ways similar to those of crosslinking, because, like crosslinks, the crystallites tie the individual chains together. Unlike crosslinks, though, the crystallites do not form covalent bonds between polymer chains and will generally melt before the polymer degrades and solvents that form strong secondary bonds with the chains can dissolve them (rather than just swell a crosslinked polymer).
The fringed micelle model has been superseded as new information has led to the development of more advanced models. Nevertheless, it still does a good job of qualitatively predicting the effects of crystallinity on the mechanical properties of the polymers.
4.6.2 Lamellar Crystals 1–7
The first direct observation of the nature of polymer crystallinity resulted from the growth of single crystals from dilute solution. Either by cooling or by evaporation of solvent, thin pyramidal or plate-like polymer crystals (lamellae) were precipitated from dilute solutions (Figure 4.5). These crystals were on the order of 10 μm along a side and only about 0.01 μm thick. This was fine, except that X-ray measurements showed that the polymer chains were aligned perpendicular to the large flat faces of the crystals, and it was known that the extended length of the individual chains was on the order of 0.1 μm. How could a chain fit into a crystal one-tenth of its length? The only answer is that the chain must fold back on itself, as shown in Figure 4.5. Two competing models of chain folding are illustrated: either the polymer folds back neatly on itself or several chains align for short distances with amorphous regions outside the crystal.
Figure 4.5 Polymer single crystals in flat lamellae. Two concepts of chain reentry are illustrated.
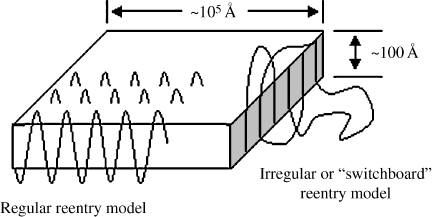
This folded-chain model has been well substantiated for single polymer crystals. The lamellae are about 50–60 carbon atoms thick, with about five carbon atoms in a direct reentry fold. The atoms in a fold, whether direct or indirect reentry, can never be part of a crystal lattice.
It is now well established that similar lamellar crystallites exist in bulk polymer samples crystallized from polymer melts, although the lamellae may be up to 1 μm thick. Recent results support the presence of a third, interfacial region between the crystalline lamellae and the amorphous phase. This interfacial phase can make up about 10–20% of the material. Furthermore, there does not seem to be much, if any, direct-reentry folding of chains in bulk (or melt)-crystallized lamellae. This is illustrated in Figure 4.6. Orientation of the lamellae along with additional orientation and crystallization in the interlamellar amorphous regions, as in the fringed micelle model, is usually invoked to explain the increase in the degree of crystallinity with drawing (stretching).
Figure 4.6 Compromise model showing folded-chain lamellae tied together by interlamellar amorphous chains.
4.6.3 Spherulites
Not only are polymer chains often arranged to form crystallites but also these crystallites often aggregate into supermolecular structures known as spherulites. Spherulites are in some ways similar to the grain structure found in metals. They grow radially from a point of nucleation until other spherulites are encountered. Thus, the size of the spherulites can be controlled by the number of nucleation sites present, with more nuclei resulting in more but smaller spherulites. They are typically about 0.01 mm in diameter and have a Maltese cross appearance when viewed between polarizing filters (Figure 4.7a). Figure 4.7 shows how the polymer chains are thought to be arranged in the spherulites.
Figure 4.7 Spherulite crystals: (a) appearance between crossed polarizing filters; (b) branching of lamellae; (c) orientation of chains in lamellae.

Large spherulites, which can grow as a polymer cools, contribute to brittleness in polymers and also scatters a lot of light. To minimize brittleness and enhance transparency, nucleating agents are often added or the polymer is shock-cooled (which increases the nucleation rate) to promote smaller spherulites.
4.7 Extended Chain Crystals
Polymers crystallized from a quiescent melt (such as those in Table 4.1) will have, in general, a random orientation of the chains at the macroscopic level. While the chains in any crystallite are oriented in a particular direction, the multiple crystallites are randomly oriented. It has long been known that if the chain axes could share a common orientation at the macroscopic level, the material would have superior mechanical properties in the orientation direction, since the chains would be arranged most efficiently to support a stress. In fact, fiber drawing does just this to a certain extent, which is why it is practiced.
Polymers crystallized while being subjected to an extensional flow (drawing), which tends to disentangle the chains and align them in the direction of flow, form fibrillar structures. These are believed to be extended-chain crystals, in which the chains are aligned parallel to one another over great distances, with little or no chain folding 8. When fibers of such materials are further drawn, a super-strong fiber results. Very high molecular weight polymers are favored for this purpose. The longer chains align more readily, and there are fewer crystalline defects due to chain ends. Also, formation of the fibers from relatively dilute solution allows easier disentanglement and better alignment of the chains.
For linear polyethylene fibers made in this fashion, the tensile modulus (a measure of the strength of a material, which is defined more rigorously in Chapter 16) of 44 GPa (6.4 × 106 psi) compares well with steel (which is about 206 GPa or 30 × 106 psi) but has a density 7.6 times as great! PE fibers with a tensile strength of 1.8 GPa (2.6 × 105 psi) have also been claimed 9. Compare these figures with those for ordinary, quiescently crystallized HDPE in Table 4.1.
Extended-chain crystals have also been identified as tying together lamellae in bulk-crystallized polymers and forming the core (“skewer”) of the interesting “shish kebab” structures grown from dilute solutions subjected to shearing 10.
4.8 Liquid Crystal Polymers 11
As noted above, if polymer chains can be aligned in the molten state (the polymer melt) prior to crystallization, high degrees of extended-chain crystallinity may be formed, imparting remarkable mechanical properties, at least in the chain direction. Another way of doing it is by starting with molecules that show a degree of order in the liquid phase; these are generally made from rigid monomers that have phenyl groups that become part of the polymer backbone. Such liquid-crystalline materials have been known for years, but until fairly recently were limited to relatively small molecules. Now, however, several types of polymers are known that exhibit liquid-crystalline order, either lyotropic (that become ordered in solution) or thermotropic (that become ordered in the melt) 12.
Kevlar® is an aromatic polyamid (“aramid”) with the repeat unit:
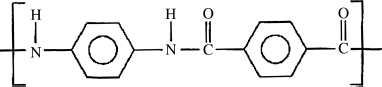
It is spun into fibers from a lyotropic liquid-crystalline solution in concentrated H2SO4. The solution is extruded through small holes into a bath that leaches the acid out of the polymer, forming the fibers (through a “wet spinning” process, as discussed in Chapter 17). Because the molecules are oriented prior to crystallization, the fibers maintain a high degree of extended-chain crystalline order in the fiber direction, imparting remarkable strength. Table 4.2 compares some properties of these fibers with those of ordinary nylon 6/6 fibers. With a density of only 1.44 g/cm3, they compare very favorably with other reinforcing fibers (glass, graphite, etc.) on a strength per weight basis. As a result, Kevlar fibers are used in bullet-proof vests and other ballistic armor, as a tire cord (replacing steel belts to improve strength and offering sidewall puncture resistance as well), and for reinforcement in high-strength composites.
Table 4.2 Comparison of Liquid-Crystalline Kevar 49 Fibers with Nylon 6/6 Fibers 13.
| Kevlar 49 | Nylon 6/6 | |
| Tensile strength, GPa, psi | 2.95 (4.3 × 105) | 1.28 (1.8 × 105) |
| Tensile modulus, GPa, psi | 130 (19 × 106) | 6.2 (3.0 × 105) |
| Elongation to break, % | 2.3 | 19 |
Several thermotropic aromatic copolyesters have also been commercialized. Vectra A® is reported to have the repeating units
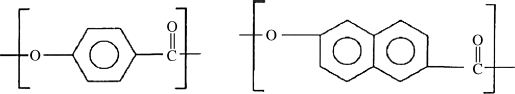
and Xydar have the repeat units
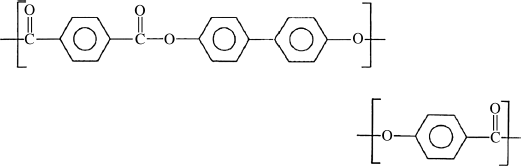
These thermotropic liquid-crystalline polymers have high melting points but can be melt-processed like other thermoplastics. The macroscopic orientation of the extended-chain crystals depends on the orientation imparted by flow during processing (molding, extrusion, etc.). Because of the fibrous nature of the extended-chain crystals, these plastics behave as “self-reinforced composites,” with excellent mechanical properties, at least in the chain direction. This is illustrated in Table 4.3 for molded specimens of a liquid-crystalline copolyester of ethylene glycol, terephthalic acid, and p-hydroxybenzoic acid 14. In the direction parallel to the flow, the properties listed in Table 4.3 favorably compare with ordinary crystalline thermoplastics (nylons, polyesters) reinforced with up to 30% glass fibers.
Table 4.3 Properties of a Molded Liquid-Crystalline Copolyester 14.
| || to Flow | ⊥ to Flow | |
| Tensile strength, MPa | 107 | 28.4 |
| Elongation, % | 8 | 10 |
| Flexural modulus, GPa | 11.8 | 1.67 |
| Linear coefficient of expansion, °C−1 | 0 | 4.5 × 10−5 |
It is obvious from the repeat units above that the liquid-crystalline behavior is promoted by highly aromatic chains. The phenyl rings inhibit rotation, resulting in stiff, rigid, extended chains, and because they are nearly planar, they stack next to one another, promoting long-range order in both the liquid and the solid states.
Thermotropic and lyotropic liquid crystals behave in a reversible manner as the temperature and the solvent are changed, respectively. The crystals change their alignment from highly ordered to amorphous as the crystals reversibly come apart and reform. These kinds of polymer crystals have found wide usage in electronics, in the form of liquid crystal displays (LCDs). Here, the crystallinity can be switched on and off thermally, electrically, or by a change in solution properties. Taking advantage of the opaque/transparent transition as polymers change from crystalline to amorphous, a display either allows or prevents viewing a backlit display (or alternately change the pattern of reflected light, as in many calculators).
Problems
1. Schultz, J.M., Polymer Material Science, Prentice-Hall, Englewood Cliffs, NJ, 1974.
2. Wunderlich, B., Macromolecular Physics, Vol.1, Crystal Structure, Morphology, Defects, Academic, New York, 1973.
3. Tadukoru, H. Structure of Crystalline Polymers, Wiley-Interscience, New York, 1979.
4. Mandlekern, L. Chapter 4 in Physical Properties of Polymers, American Chemical Society, Washington, DC, 1984.
5. Bovey, F.A., Chapter 5 in Macromolecules: An Introduction to Polymer Science, F.A. Boveyand F.H. Winslow (eds), Academic, New York, 1979.
6. Geil, P.H., Polymer Single Crystals, Interscience, New York, 1963.
7. Oppenlander, G.C., Science 159, 1311 (1968).
8. Southern, J.H. and R.S. Porter, J. Appl. Polym. Sci.14, 2305 (1970); J. Macromol. Sci. Phys.B4, 541 (1970).
9. Kavesh, S. and D.C. Prevorsek, U.S. Patent 4,413,110.
10. Pennings, A.J., J. Polym. Sci. (Symposia) 59, 55 (1977).
11. Weiss, R.A. and C.K. Ober (eds), Liquid-Crystalline Polymers, American Chemical Society, Washington, DC, 1990.
12. Blumstein, A. (ed.) Liquid Crystalline Order in Polymers, Academic, New York, 1978.
13. DuPont product literature.
14. Menges, G. and G. Hahn, Modern Plastics, October 1981, p. 56.