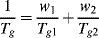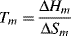Chapter 6

Thermal Transitions in Polymers

6.1 Introduction

The reader should be familiar with thermal transitions, particularly the melting (or freezing) and the boiling points of pure substances. Polymers are a bit more complex; their size leads to the definition of a new term, the glass transition temperature, which divides glassy from rubbery behavior. The polydispersity of polymeric samples also leads to melting point ranges. Alternately, the boiling point is largely unimportant for polymers, since they degrade well before macromolecules vaporize. This chapter focuses on some of the unique thermal behavior observed in polymers and explains why polymers have a thermal history that is crucial in determining physical properties.

6.2 The Glass Transition

It has long been known that amorphous polymers can exhibit two distinctly different types of mechanical behavior. Some, such as poly(methyl methacrylate) (PMMA), trademarked as Lucite® or Plexiglas®, and polystyrene (PS), are hard, rigid, glassy plastics at room temperature. Other polymers, for example, polybutadiene, poly(ethyl acrylate), and polyisoprene, are soft, flexible rubbery materials. If, however, PS and PMMA are heated to around 125 °C, they exhibit typical rubbery properties; when a rubber ball is cooled in liquid nitrogen, it becomes rigid and glassy and shatters when an attempt is made to bounce it. So, there is some temperature, or narrow range of temperatures, below which an amorphous polymer is in a glassy state and above which it is rubbery. This temperature is known as the glass transition temperature, Tg. The glass transition temperature is a property of the polymer, and whether the polymer has glassy or rubbery properties depends on whether its application temperature is above or below its glass transition temperature. Note that the Tg is a property of the amorphous regions of polymers; however, since no polymer is 100% crystalline, the Tg is important for all polymeric materials.

6.3 Molecular Motions in an Amorphous Polymer

To understand the molecular basis for the glass transition, the various molecular motions occurring in an amorphous polymer mass may be broken into four categories.

1. Translational motion of entire molecules that permits flow.
2. Cooperative wriggling and jumping of segments of molecules approximately 40–50 carbon atoms in length, permitting flexing and uncoiling, that lead to elasticity.
3. Motions of a few atoms along the main chain (five or six, or so) or of side groups on the main chains.
4. Vibrations of atoms about equilibrium positions, as occurs in crystal lattices, except that the atomic centers are not in a regular arrangement in an amorphous polymer.

Motions 1–4 above are arranged in order of decreasing activation energy (as well as decreasing number of atoms involved in the motion), that is, smaller amounts of thermal energy (kT1) are required to produce them. The glass transition temperature is thought to be that temperature at which motions 1 and 2 are pretty much “frozen out,” and there is only sufficient energy available for motions 3 and 4. Of course, not all molecules possess the same energies at a given temperature. The molecular energies follow a Boltzmann distribution, and even below Tg, there will be occasional type 2 and even type 1 motions, which can manifest themselves over extremely long periods of time.

6.4 Determination of Tg

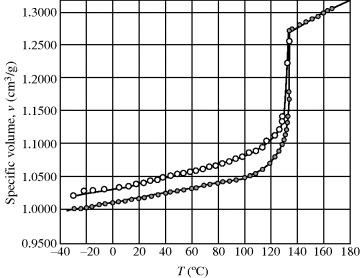
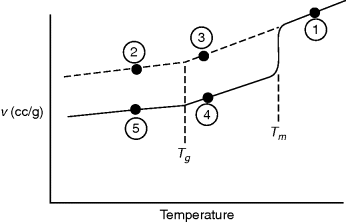
How is the glass transition temperature studied? A common method is to observe the variation of some thermodynamic property with T, for example, the specific volume, as shown in Figure 6.1. As temperature rises, the polymer expands, with a change to a higher slope in the v versus T plot above the glass transition temperature.

Figure 6.1 Specific volume (v) versus temperature for poly(vinyl acetate) [1].

img

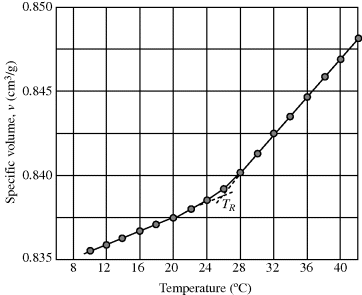
The value of Tg determined in this fashion will vary somewhat with the rate of cooling or heating. This reflects the fact that long, entangled polymer chains cannot respond instantaneously to changes in temperature and illustrates the difficulty in making thermodynamic measurements on polymers. It often takes an extremely long time to reach equilibrium, if indeed it is ever reached, and it is difficult to be sure if and when it is reached. Strictly speaking, the glass transition temperature should be defined in terms of equilibrium properties or at least those measured with very low rates of temperature changes. Also, a sharp “break” in the property is never observed, but Tg can always be established within a couple of degrees by extrapolation of the linear regions (as shown in Figure 6.1). Other properties such as refractive index may also be used to establish Tg.

In contrast to a change in slope at the glass transition, a thermodynamic property such as specific volume exhibits a discontinuity with temperature at the crystalline melting point in polymers as in other materials (Figure 6.2). The glass transition is therefore known as a second-order thermodynamic transition (where v versus T is continuous and dv/dT versus T is discontinuous) in contrast to a first-order transition such as the melting point (where v versus T is discontinuous).

Figure 6.2 Specific volume–temperature relations for linear polyethylene (Marlex-50). img: Specimen slowly cooled from melt to room temperature prior to fusion. img Specimen crystallized at 130 °C for 40 days, then cooled to room temperature prior to fusion [2].

img

Tg characterizes the amorphous phase. Since all polymers have at least some amorphous material (they cannot be 100% crystalline), they all have a Tg, but not all polymers have a crystalline melting point, they cannot have if they do not crystallize (and many polymers will degrade before they melt).

Transitions in polymers are rapidly and conveniently studied using differential scanning calorimetry (DSC) [3]. Small samples (~10 mg) of the polymer and an inert reference substance (one that undergoes no transitions in the temperature range of interest) are mounted in a block with a heater for each and thermocouples to monitor temperatures. The thermodynamic property monitored here is the enthalpy. The power supplied to each heater is monitored and adjusted to keep the sample and the reference at the same temperature as both are heated at a programmed rate (typically 5–20 °C/min). At Tg, the heat capacity of the sample suddenly increases, requiring more power (relative to the reference) to maintain the same temperatures. This differential heat flow to the sample (endothermic) causes a drop in the DSC curve (Figure 6.3). At Tm, the sample crystals want to melt at constant temperature, so a sudden input of large amounts of heat is required to keep the sample temperature even with the reference temperature. This results in the characteristic endothermic melting peak. Crystallization, in which large amounts of heat are given off at constant temperature, gives rise to a similar but exothermic peak (although this peak is missing for many polymers that either do not crystallize appreciably or are already crystalline before heating). By measuring the net energy flow to or from the sample, heat capacities and heats of fusion can be determined. Decomposition (endothermic) and oxidation (exothermic) reactions can also be conveniently studied (as can exothermic polymerization reactions, as discussed later).

Figure 6.3 Schematic DSC curve. This is what would be observed on heating a material from state 2 (Example 6.8, Figure 6.5) to state 1.

img

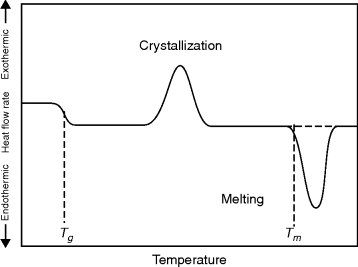
In Figure 6.3, the crystallization and melting peaks are shown as occurring over a temperature range, and the rates of heating (or cooling) can broaden (for higher dT/dt rates) or narrow (for slow heating or cooling) these peaks. However, even with a very slow temperature ramp, the melting transition will occur over a range of temperatures rather than being well defined at a single temperature (e.g., compared with a pure low molecular weight substance, say ice, polymer samples are polydisperse, having a range of crystallite sizes and having entanglements and complex secondary interactions that cause broad melting peaks).

A DSC is programmed to heat the sample at a constant rate. The higher the rate, the quicker the measurement, a practically desirable result. Unfortunately, because polymer chains cannot respond instantaneously to the changing temperature, the measurement is further from equilibrium. The dependence of the measured Tg or Tm on heating rate is at least partially responsible for the range of values observed in the literature. To approach the true equilibrium values, very low heating rates should be used or, better yet, several heating rates should be used and the results extrapolate back to zero heating rate. Because of the time and effort involved, this is rarely done. Newer DSC models have a temperature modulation program that allows fine-tuning of these measurements to more accurately measure Tg and Tm. Dynamic mechanical measurements (see Chapter 16) can also provide useful information on thermal transitions.

6.5 Factors that Influence Tg [4]

In general, the glass transition temperature depends on five factors.

1. The free volume of the polymer vf, which is the volume of the polymer mass not actually occupied by the molecules themselves (think of a kitchen sponge, but on a molecular level), that is, vf = v − vs, where v is the specific volume of the polymer mass and vs is the volume of the solidly packed molecules. The higher vf, the more room the molecules will have to move around, resulting in a lower Tg. It has been estimated that for all polymers vf/v ≈ 0.025 at Tg.
Example 6.1 Glass transition temperatures have been observed to increase at pressures of several thousand psi. Why?
Solution. High pressures compress polymers, reducing v. Since vs does not change appreciably, vf is reduced.
2. The attractive forces between the molecules––the more strongly they are bound together, the more thermal energy will be required to produce motion. The solubility parameter δ (defined explicitly in Chapter 7) is a measure of intermolecular forces, thus Tg increases with δ. Polyacrylonitrile, because of the frequent, strong polar bonding between chains, has a Tg higher than its degradation temperature and therefore, though linear, is not thermoplastic.

img

3. The internal mobility of the chains, that is, their freedom to rotate about bonds. Figure 6.4 shows potential energy as a function of rotation angle about a bond in a polymer chain. For a carbon–carbon bond, there are three other bonds to each carbon (assuming the backbone does not have double bonds): two will be pendent groups and the third will be the continuation of the polymer backbone. The minimum energy configuration, arbitrarily chosen as θf = 0, is the position where the largest substituents (the rest of the chain) are far away from each other as possible. As the bond is rotated, the substituent groups are brought into juxtaposition, and energy is required to “push them over the hump.” The maximum energy is needed to get the two chain substituents past one another, and this energy must be available if complete rotation is to be obtained. Rotation is necessary for type 1 and type 2 motions.

Figure 6.4 Rotation about a bond in a polymer chain backbone, viewed along the bond. The dotted substituents are on the rear carbon atom.

img

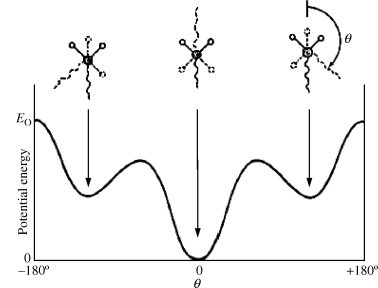
Table 6.1 shows how Tg increases with Eo, the potential energy, for a series of polymers with approximately the same δ. Note how the ether oxygen “swivels” in the silicone chain permitting very free rotation.

Table 6.1 Effect of Potential Energy on Tg for Selected Polymers [4]

img

Example 6.2 Poly(α-methyl styrene) has a higher Tg than PS. Why?
img
Solution. The methyl group introduces extra steric hindrance to rotation, giving a higher Eo.
4. The stiffness of the chains––chains that have difficulty coiling and folding will have higher Tg values. This stiffness usually goes hand-in-hand with high Eo, therefore it is difficult to separate the effects of 3 and 4.

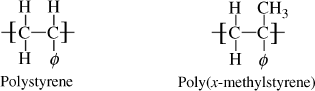
Chains with parallel bonds in the backbone (ladder-type polymers), for example, polyimides (Example 2.4R), and those with highly aromatic backbones, such as aramids (see Chapter 4.8) have extremely stiff chains and, therefore, tend to have high Tg values. This makes these polymers mechanically useful at elevated temperatures but also very difficult to process.

5. The chain length––as do many mechanical properties of polymers, the glass transition temperature varies according to the empirical relation:

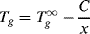
(6.1) equation

where C is a constant for the particular polymer, and Tg∞ is the asymptotic value of the glass transition temperature for infinite chain length. This reflects the increased ease of motion for shorter chains. The decrease in Tg with x is only noticeable at relatively low chain lengths. For most commercial polymers, x is high enough so that Tg ≈ Tg∞.

Example 6.3 Measurements such as those described above show that the addition of a small molecular weight chemical known as an external plasticizer (see Chapter 7) softens a polymer by reducing its glass transition temperature. Explain.
Solution. The plasticizer molecules pry apart the polymer chains, in essence increasing the free volume available to the chains (although not truly free, the small plasticizer molecules interfere with chain motions much less than would other chains). Also, by forming secondary bonds with the polymer chains themselves, type 1 and type 2 motions are easier.

6.6 The Effect of Copolymerization on Tg

The glass transition temperatures for random copolymers vary monotonically with composition between those of the homopolymers. They can be approximated fairly well from knowledge of the Tg values of the homopolymers, Tg1 and Tg2, with the empirical relation:

(6.2) equation

where the w's are weight fractions of the monomers in the copolymer. This relation forms the basis for a method of estimating the Tg values of highly crystalline polymers, where the properties of the small amount of amorphous material are masked by the majority of crystalline material present. If a series of random copolymers can be produced in which the randomness prevents crystallization over a certain composition range, then Equation (6.2) can be used to extrapolate to w1 = 1 or w2 = 1, giving the Tg values of the homopolymers. This method is open to question because it assumes that the presence of major amounts of crystallinity does not restrict the molecular response in the amorphous regions. In fact, the Tg values of highly crystalline polymers (polyethylene, in particular) are still open to debate.

6.7 The Thermodynamics of Melting

The crystalline melting point Tm in polymers is a phase change similar to that observed in low molecular weight organic compounds, metals, and ceramics.

The Gibbs free energy of melting is given by

(6.3) 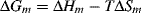equation

At the equilibrium crystalline melting point, Tm, ΔG = 0, therefore

(6.4) equation

Now ΔHm is the energy needed to overcome the crystalline bonding forces at constant T and P, and is essentially independent of chain length of high polymers. For a given mass or volume of polymer, however, the shorter the chains are, the more randomized they become upon melting, giving a higher change in entropy on mixing, ΔSm. (For a more detailed description of this in connection with solutions, see Chapter 7.) Thus, the crystalline melting point decreases with decreasing chain length and in a polydisperse polymer, the distribution of chain lengths give a distribution of melting points.

Equation (6.4) also indicates that chains that are strongly bound in the crystal lattice, that is, have a high ΔHm, will have a high Tm, as expected. Also, the stiffer and less mobile chains, those that can randomize less upon melting and therefore have low ΔSm, will tend to have higher Tm values.

Example 6.4 Discuss how the crystalline melting point varies with n in the “nylon n” series, where n can be varied.
img
Solution. Increasing values of n dilute the nylon linkages that are responsible for interchain hydrogen bonding, and thus should lower ΔHm and the crystalline melting point. As n goes to infinity, the structure approaches that of linear polyethylene. This should represent the asymptotic minimum Tm, with the chains held together only by van der Waal's forces.

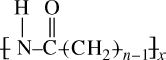
Table 6.2 illustrates the variation in Tm and some other properties with n for some commercial members of the nylon series.

Table 6.2 Variation of Properties with n for Nylon n's.

img

Example 6.5 Consider the following classes of linear, aliphatic polymers:
img
For given values of n and x, the crystalline melting points increase from left to right, as indicated. Explain.
Solution. The polyurethane chains contain the –O– swivel, thus they are the most flexible, having the largest ΔSm, and having the lowest Tm. Hydrogen bonding, and thus ΔHm, is roughly comparable in the polyurethanes and polyamides. The polyureas and polyamides should have chains of comparable flexibility (no swivel), but with the extra –NH–, the polyureas form stronger or more extensive hydrogen bonds, and therefore have a higher ΔHm than the polyamides.
Example 6.6 Experiments show that uniaxial orientation (drawing) increases the crystalline melting point. Explain.
Solution. The entropy of melting, ΔSm, is the difference between the entropies of the amorphous and the crystalline materials:
img
drawing align the amorphous chains in the direction of stretch, increasing order, reducing Sa and, thus, ΔSm. According to Equation (6.4), this increases Tm.
Example 6.7 Liquid-crystalline polyesters (Section 4.8) have significantly higher Tm values than non-LC polyesters. For example, Xydar has a Tm value in the vicinity of 400 °C, whereas poly(ethylene terephthalate), shown in Example 2.4D, has a Tm of 267 °C and poly(butylene terephthalate), shown in Example 2.4C, has a Tm of 224 °C. Explain.
Solution. Here, one might expect the ordinary polyesters to have higher ΔHm's, particularly the PET, because of the decreased spacing between the polar ester linkages, so the explanation must lie in the ΔSm's. Because thermotropic LCPs by definition maintain considerable order in the molten state, they randomize less upon melting and therefore have lower Sm's than non-LC polyesters.

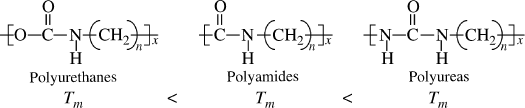
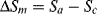
The crystalline melting point also increases a bit with the degree of crystallinity of a polymer. For example, low-density polyethylene (approximately 50% crystalline) has a Tm of about 115 °C, whereas high-density polyethylene (approximately 80% crystalline) melts at about 135 °C. This can be explained by treating the amorphous material as an impurity. It is well known that introducting an impurity lowers the melting point of common materials. In a similar fashion, greater amounts of noncrystalline “impurities” lower the crystalline melting point of a polymer.

6.8 The Metastable Amorphous State

Since polymer chains are largely immobilized below Tg, if they are cooled rapidly through Tm to below Tg, it is sometimes possible to obtain a metastable amorphous state in polymers that would be crystalline at equilibrium. This rapid cooling effectively locks the chains in a random, amorphous state. As long as the material is held below Tg, this metastable amorphous state persists indefinitely. When annealed above Tg (and below Tm), the polymer crystallizes, as the chains gain the mobility necessary to pack into a lattice. This behavior leads to classifying polymers as materials that have a thermal history, indicating that the rate of cooling affects crystallinity (and other properties).

Poly(ethylene terephthalate), from Example 2.4D, because of its bulky chain structure, crystallizes sluggishly and is therefore relatively easy to obtain in the metastable amorphous state. When desired, crystallinity can be promoted by slow cooling from the molten state, annealing between Tg and Tm, or by the addition of nucleating agents. PET has important commercial applications both in the metastable amorphous state (soda bottles) and in the crystalline state (textile fibers, microwaveable food trays, molding resin). On the other hand, no one has yet succeeded in producing an amorphous polyethylene, with its much more flexible chains, although the degree of crystallinity can be reduced substantially by rapid cooling (Figure 6.2). Interestingly, metallurgists can also produce amorphous metals by rapidly cooling certain alloys.

Example 6.8 Poly(ethylene terephthalate), or PET (Mylar, Dacron), is cooled rapidly from 300 °C (state 1) to room temperature. The resulting material is rigid and perfectly transparent (state 2). The sample is then heated to 100 °C (state 3) and maintained at that temperature, during which time it gradually becomes translucent (state 4). It is then cooled down to room temperature and is again found to be rigid, but is now translucent rather than transparent (state 5). For this sample of PET, Tmf = 267 °C and Tgf = 69 °C. Sketch a general specific-volume versus temperature curve for a crystallizable polymer, illustrating Tg and Tm, and show the locations of states 1–5 for this PET sample.
Solution. Figure 6.5 illustrates the general v versus T curve for a crystallizable polymer. The dotted upper portion represents the metastable amorphous material obtainable by rapid cooling. The history of the PET sample is shown in the diagram. The metastable amorphous material (transparent, state 2) is obtained by rapid cooling to below Tg; however, when heated to state 3 (between the Tg and Tm), the sample undergoes the process of annealing, becoming more crystalline. The schematic DSC curve in Figure 6.3 illustrates what would be observed in a DSC measurement starting with a material in the metastable amorphous state (state 2) and heating it to above Tm (state 1).

Figure 6.5 Specific volume–temperature relation for crystallizable polymers. Numbers apply to Example 6.8.

img
Note the change in slope at the glass transition temperature. Also, as long as state 3 is above Tg, the chains will have enough mobility to rearrange (eventually) into a more stable semicrystalline state. Thus (comparing states 2 and 5), this information is not enough to simply state the molecular weight of PET and temperature to determine the properties; the thermal history influences crystallinity that can have a profound effect on the properties of the material (from density to optical properties and mechanical behavior). Thus, this is a great example of why polymers have a thermal history. State 5 could also have been reached by slowly cooling the PET sample from state 1.

Polymer blends, which are mixtures of two or more different homopolymers, are also commonly used in commercial materials. Except in the rare case where interpolymer crystallites can form, blends exhibit multiple Tg's and Tm's, one for each component of the blend.

6.9 The Influence of Copolymerization on Thermal Properties

Compared with polymer blends, copolymers have only one Tg and one Tm. The influence of random copolymerization on Tm and Tg is interesting and technologically important. Occasionally, if two repeating units are similar enough sterically to fit into the same crystal lattice, random copolymerization will result in copolymers whose crystalline melting points vary linearly with composition between those of the pure homopolymers. Much more common, however, is the case where the homopolymers form different crystal lattices because of steric differences. The random incorporation of minor amounts of repeating unit B with A will disrupt the A lattice, lowering Tm beneath that of homopolymer A, and vice versa. In an intermediate composition range, the disruption will be so great that no crystallites can form and the copolymers will be completely amorphous. A phase diagram for such a random copolymer system is shown in Figure 6.6.

Figure 6.6 Phase diagram for a random copolymer system.

img

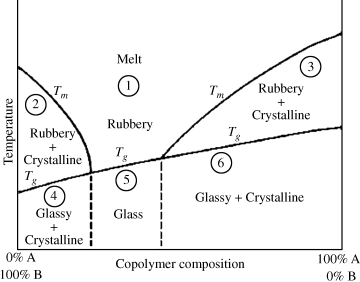
The physical properties of random copolymers are determined from their composition and the temperature, as can be found in a diagram such as the one qualitatively shown in Figure 6.6. In region 1, the polymer is a homogeneous, amorphous, and, if pure, transparent material. The distinction between melt and rubbery behavior is not sharp; at higher temperatures, the material flows more easily and becomes less elastic in character (assuming that the polymer does not reach degradation temperatures). It should be kept in mind, though, that the viscosities of polymer melts, even well above Tg or Tm, are far greater than those encountered in nonpolymeric materials.

A copolymer in region 5 is a typical amorphous, glassy polymer: hard, rigid, and usually brittle. Again, if the polymer is pure, it will be perfectly transparent. PMMA (Lucite, Plexiglas) and PS are familiar examples of homopolymers with these properties.

Copolymers in regions 2 and 3 consist of rigid crystallites dispersed in a relatively soft, rubbery, amorphous matrix. Since the refractive indices of the crystalline and amorphous phases are in general different, materials in these regions will be translucent to opaque, depending on the size of the crystallites, the degree of crystallinity, and the thickness of the sample. Since the crystallites restrict chain mobility, the materials are not elastic, but the rubbery matrix confers flexibility and toughness. The stiffness depends largely on the degree of crystallinity; the more rigid crystalline phase present, the stiffer the polymer. Polyethylene (e.g., flexible squeeze bottles or rigid bleach bottles) is a good example of a homopolymer with these properties, typical of a polymer that is between its Tg and Tm at room temperature.

Copolymers in regions 4 and 6 consist of crystallites in an amorphous, glassy matrix. Since both phases are rigid, the materials are hard, stiff, and rigid. Again, the two phases impart opacity. Nylon 6/6 and nylon 6 are examples of homopolymers in a region below both Tg and Tm at room temperature.

6.10 Effect of Additives on Thermal Properties

A number of different compounds are used as polymer additives to tailor the properties of materials for their end-use. As discussed in detail in Chapter 18, these additives include dyes, fillers, plasticizers, and a variety of other compounds. Because each of these additives gets between polymer chains (at least to some extent), they reduce the number of polymer–polymer interactions and cause an increase in chain mobility (when compared to the pure polymer at the same temperature). This causes a drop in Tg (which is exactly what a plasticizer is designed to do, Figure 6.7). This decrease in Tg depends on the thermodynamic compatibility of the additive with the polymer. For some fillers, this may be quite low, causing little change in Tg, but for chemical additives that interact with the polymer, Tg can be reduced significantly. The thermodynamics of polymer solutions and polymer additives are discussed in detail in the next chapter. The melting point of a polymer with an additive will not be influenced greatly, but the degree of crystallinity (and crystal sizes) will drop markedly, as the additive will interfere in the formation of regular crystals.

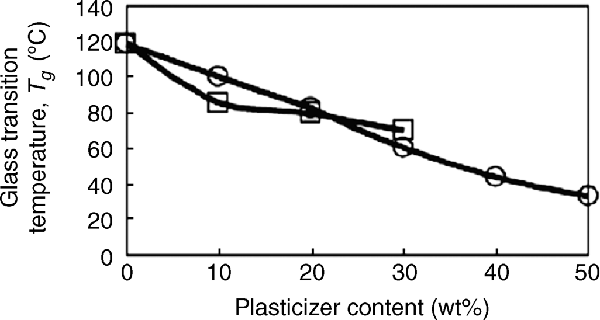
Figure 6.7 Effect of adding dioctyl phthalate (DOP) (a plasticizer), squares, or imidazolium ionic liquid additives (bmimPF6 or hmimPF6), circles, to PMMA on Tg [5]. Reproduced by permission of the Royal Society of Chemistry.

img

6.11 General Observations About Tg AND Tm

Some other useful observations regarding Tg and Tm are that for polymers with a symmetrical repeating unit, such as polyethylene –(CH2–CH2)– and poly(vinylidene chloride), or Saran®, –(CH2–CCl2)–, Tg/Tm ≈ 1/2 (for absolute T's); for unsymmetrical repeating units, such as polypropylene –(CH2–CHCH3)– and polychlorotrifluoroethylene –(CF2–CFCl)–, Tg/Tm ≈ 2/3. These are just rough estimates, but in all cases Tg < Tm.

6.12 Effects of Crosslinking

To this point, the discussion has centered on non-crosslinked (and generally linear, rather than branched) polymers. Light crosslinking, as in rubber bands, will not alter things appreciably. However, higher degrees of crosslinking, if formed in the amorphous molten state or in the solution, as is usually the case, will hinder the alignment of chains necessary to form a crystal lattice and will thus reduce or prevent crystallization. Similarly, crosslinking restricts chain mobility and causes an increase in the apparent Tg. When the crosslinks are more frequent than every 40–50 main chain atoms, the type 2 motions necessary to reach the rubbery state can never be achieved and the polymer will degrade before reaching Tg.

6.13 Thermal Degradation of Polymers

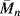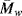As mentioned earlier in this chapter, several polymers start to degrade before reaching a melting point. All polymers eventually degrade given enough heating. The degradation process is sort of a depolymerization, except the bonds break randomly along the backbone, resulting in a smaller img and img (and higher PI). The reductions in the molecular weight also degrade the mechanical properties of the polymers. In many applications, additives are used to stabilize polymers that may be used at high temperatures. However, anyone who has microwaved a plastic bowl to the point of deformation understands that polymers can degrade appreciably even at moderate temperatures, especially when compared to glass or metal materials.

PVC is an example of a polymer that self-catalyzes its thermal degradation. Beginning at temperature around 160 °C, HCl is formed as a byproduct of thermal degradation, and, even worse, the acid catalyzes further degradation of PVC. This is why PVC is not used for high-temperature applications, and even for moderate temperatures, a thermal stabilizer is normally added.

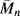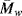Thermal degradation is one of the primary challenges in effective polymer recycling. Although thermoplastics can be melted and reused, uneven temperature distributions (or the heat evolved while grinding polymers) can cause some degree of thermal degradation, reducing img and img. This is partly why recycled polymers are most often used in applications where high mechanical strength is less important, such as park benches and grocery bags.

6.14 Other Thermal Transitions

Thermal transitions other than Tg and Tm are sometimes observed in polymers. Some polymers possess more than one crystal form, so there will be an equilibrium temperature of transition from one to another. Similarly, second-order transitions below Tg occur in some materials (Tg is then termed the α transition, the next lower is the β transition, and so forth). These are attributed to motions of groups of atoms smaller than those necessary to produce Tg (type 3 motions, Section 6.2). These transitions may strongly influence properties. For example, tough amorphous plastics (e.g., polycarbonate) have such a transition well below room temperature, while brittle amorphous plastics (e.g., PS and PMMA) do not.

The existence of another transition above Tg has been claimed, but is still the subject of considerable controversy. This Tll (liquid–liquid transition) presumably represents the boundary between type 1 and type 2 motions. It has been observed in a number of systems [6–8], and it has been suggested that Tll ≈ 1.2 Tg (in absolute temperature) for all polymers [6]. For each article that reports Tll, however, it seems that there is another that claims that Tll results from impurities (traces of solvent or unreacted monomer) in the sample or is an artifact of the experimental or data-analysis technique [9, 10].

Problems

1. Pure nylon 6/6 (see Example 2.4E for the structure) is a white, opaque plastic at room temperature. If isophthalic acid (HOOC–ϕ–COOH, with the acids in the meta positions, on the first and third carbons) is substituted for adipic acid in the polymerization, a rigid, transparent plastic is obtained. By varying the ratio of the two acids, one can get a series of polyamide copolymers. Sketch a phase diagram like Figure 6.6 for these copolymers. Be sure to show which repeating unit goes with each composition extreme and also show the room temperature.
2. Three DSC runs are made on a semicrystalline polymer sample starting at room temperature and passing through the glass-transition temperature and melting point. Three different heating rates are used: 1, 5, and 20 °C/min. Sketch qualitatively the expected DSC thermograms to show how you think the observed Tg and Tm will vary with heating rate.
3. Injection molding consists of squirting a molten polymer into a cold metal mold. When thick parts are molded from a crystallizable polymer (e.g., polypropylene), they sometimes exhibit “sink marks,” where the surface of the part has actually sunk away from the mold wall.
a. Explain why. Hint: Polymers have very low thermal diffusivity.
b. How would an amorphous (non-crystallizable) polymer perform in injection molding?
4. Two diols, ethylene glycol (Example 2.4D) and bisphenol-A (Example 2.4N), are commercially available at low cost. Which would you choose for polyesterification with a diacid if your objective was to:
a. produce a transparent polyester and
b. obtain the higher Tg.
5. A patent claims that a new polymer forms strong, highly crystalline parts when injection molded. Furthermore, it is claimed that Tg > Tm for this material. Comment.
6. An amorphous emulsion copolymer consisting of 60 wt% methyl methacrylate (homopolymer Tg = 105 °C) and 40 wt% ethyl acrylate (homopolymer Tg = −23 °C) has been proposed as the basis of a latex paint formulation. A latex consists of tiny (≈1−10 μm) polymer particles suspended in water. After application of the paint, these particles must coalesce to form a film upon evaporation of water.
a. Would the copolymer be suitable for an outdoor paint?
b. An actual paint formulation based on this copolymer contains some medium-volatility solvent dissolved in the latex particles. This solvent is designed to evaporate over a period of a few hours after application of the paint. What is it doing there?
7. High molecular weight linear polyesters from 1,4-butanediol (HO–(CH2)4–OH) and terephthalic acid (HOOC–ϕ–COOH), with the acids in the para or opposite positions) are successful engineering plastics (materials with high mechanical strength and good thermal stability). They are, however, not used as a blister (sturdy, see-through) packaging material. A polymer for the blister-packaging market is made from the two monomers above plus isophthalic acid (meta–ϕ–(COOH)2). Explain the difference in the applications.
8. Polyethylene (Tm = 135 °C, Tg < Troom) may be lightly crosslinked by a chemical reaction with an organic peroxide at 175 °C. Heat-shrink tubing is made from such a crosslinked polyethylene. When heated at room temperature to about 150 °C, its diameter shrinks by a factor of three or four. Explain the thermal history required to make and use this material and the driving force for shrinkage when heat is applied.
9. A diagram like Figure 6.1 is prepared by heating a polymer well above its Tg and then rapidly cooling it to the desired temperature and holding it there until v is measured. Sketch v versus T curves for v measurements taken 1 min after cooling and 100 h after cooling. Illustrate how this would affect the value of Tg obtained.
10. Professor Irving Inept of MIT (Monongahela Institute of Technology) figures that he can pad his publication list by publishing a series of polymer tables. Similar to the steam tables from thermodynamics or the CRC Handbook of Chemistry and Physics, they will contain the thermodynamic properties of various polymers as functions of temperature and pressure. Discuss the difficulties associated with
a. obtaining the necessary data and
b. applying the published numbers in practice.
11. Sketch on a copy of Figure 6.5 the path of a DSC test on a materials starting in states 2 and 5 and heated to above Tm.

Notes

1. kT is the product of the Boltzmann constant and absolute temperature. It is related to energy on a molecular level and is discussed in more detail in physical chemistry.

References

1. Meares, P., Trans. Faraday Soc. 53, 31 (1957).

2. Mandelkern, L., Rubber Chem. Technol. 32, 1392 (1959).

3. Wunderlich, B., Thermal Analysis, Academic, San Diego, CA, 1990.

4. Tobolsky, A.B., Properties and Structure of Polymers, Wiley, New York, 1960, Chapter 2.

5. Scott, M.P., M. Rahman, and C.S. Brazel, Eur. Polym. J. 39, 1947 (2003).

6. Kumar, P.L., et al., Org. Coat. Plast. Chem. 44, 396 (1981).

7. Ibar, J.P., Polym. Prepr. 22(2), 405 (1981).

8. Boyer, R.F., Macromolecules 15(6), 1498 (1982).

9. Plazek, D.J., et al., J. Polym. Sci., Polym. Phys. Ed. 20(9), 1533, 1551 1565, 1575 (1982).

10. Loomis, L.D. and P. Zollar, J. Polym. Sci., Polym. Phys. Ed. 21(2), 241 (1983).