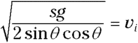Chapter 4
Following Directions: Motion in Two Dimensions
In This Chapter
 Mastering vector addition and subtraction
Mastering vector addition and subtraction
 Putting vectors into numerical coordinates
Putting vectors into numerical coordinates
 Dividing vectors into components
Dividing vectors into components
 Identifying displacement, acceleration, and velocity as vectors
Identifying displacement, acceleration, and velocity as vectors
 Understanding projectile motion
Understanding projectile motion
You aren’t limited to moving left and right or forward and backward; you can move in more than one dimension. In the real world, you need to know which way you’re going and how far to go. For example, when a person gives you directions, she may point and say something like, “The posse went 15 miles thataway!” When you’re helping someone hang a door, the person may say, “Push hard to the left!” And when you swerve to avoid hitting someone in your car, you accelerate in another direction. All these statements involve vectors.
A vector is a quantity that has both a size (magnitude) and a direction. Because physics models everyday life, plenty of concepts in physics are vectors, too, including velocity, acceleration, and force. For that reason, you should snuggle up to vectors, because you see them in just about any physics course you take. Vectors are fundamental.
Many people who’ve had tussles with vectors decide they don’t like them, which is a mistake — vectors are easy after you get a handle on them, and you get a handle on them in this chapter. We break down vectors from top to bottom and relate the characteristics of motion (displacement, velocity, and acceleration) to the concept of vectors. Here, balls fly through the air and roll off cliffs, baseball players race to make plays, and you find a great shortcut to the nearest park bench. Read on.
Visualizing Vectors
In one dimension, displacement, velocity, and acceleration are either positive or negative (see Chapter 3). For example, they may be negative if they’re to the left and positive to the right. The size of the displacement, velocity, or acceleration is given by the absolute size (regardless of sign) of the number representing it — this is the magnitude. The sign of the number indicates direction (left or right).
But what do you do if you have more than one dimension? If the object can move up and down as well as left and right, you can no longer use a single number to represent displacement, velocity, and acceleration. You need vectors. In this section, we represent vectors as arrows and show you what vector addition and subtraction look like.
Asking for directions: Vector basics
Remember: When you have a vector, you have to keep in mind two quantities: its direction and its magnitude. Quantities that have only a magnitude are called scalars. If you give a scalar magnitude a direction, you create a vector.
Visually, you see vectors drawn as arrows in physics, which is perfect because an arrow has both a clear direction and a clear magnitude (the length of the arrow). Take a look at Figure 4-1. The arrow represents a vector that starts at the arrow’s foot (also called the tail) and ends at the head.
In physics, you use a letter in bold type to represent a vector. This is the notation we use in this book; in some books, however, you see a letter with an arrow on top like this: 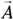 . The arrow means that this is not only a scalar value, which would be represented by A, but also something with direction.
. The arrow means that this is not only a scalar value, which would be represented by A, but also something with direction.
Say that you tell some smarty-pants that you know all about vectors. When he asks you to give him a vector, A, you give him not only its magnitude but also its direction, because you need these two bits of info together to define this vector. That impresses him to no end! For example, you may say that A is a vector at 15° above the horizontal with a magnitude of 12 meters per second. Smarty-pants knows all he needs to know, including that A is a velocity vector.
Take a look at Figure 4-2, which features two vectors, A and B. They look pretty much the same — the same length and the same direction. In fact, these vectors are equal. Two vectors are equal if they have the same magnitude and direction, and you can write this as A = B.
Looking at vector addition from start to finish
Remember: Just as you can add two numbers to get a third number, you can add two vectors to get a resultant vector. To show that you’re adding two vectors, put the arrows together so one arrow starts where the other arrow ends. The sum is a new arrow that starts at the base of the first arrow and ends at the head (pointy end) of the other.
Consider an example using displacement vectors. A displacement vector gives the change in position: the distance from the starting point to the ending point is the magnitude of the displacement vector, and the direction traveled is the direction of the displacement vector.
Assume, for example, that a passerby tells you that to get to your destination, you first have to follow vector A and then vector B. Just where is that destination? You work this problem just as you find the destination in everyday life. First, you drive to the end of vector A, and from that point, you drive to the end of vector B, just as you see in Figure 4-3.
When you get to the end of vector B, how far are you from your starting point? To find out, you draw a vector, C, from your starting point (foot, or tail, of the first vector) to your ending point (head of the second vector), as you see in Figure 4-4. This new vector represents your complete trip, from start to finish. In other words, 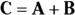 . The vector C is called the sum, the result, or the resultant vector.
. The vector C is called the sum, the result, or the resultant vector.
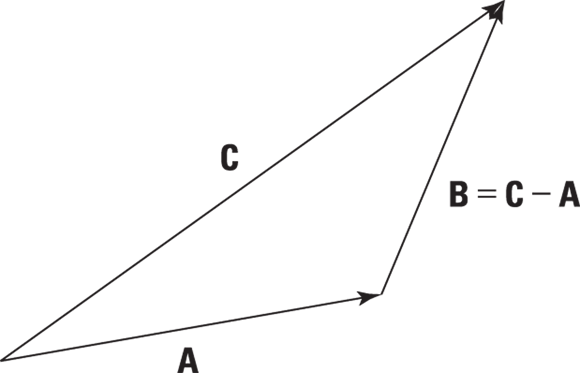
Going head-to-head with vector subtraction
You don’t come across vector subtraction very often in physics problems, but it does pop up. To subtract two vectors, you put their feet (the non-pointy parts) together; then draw the resultant vector, which is the difference of the two vectors, from the head of the vector you’re subtracting to the head of the vector you’re subtracting it from.
To make heads or tails of this, check out Figure 4-5, where you subtract A from C (in other words, C – A). As you can see, the result is B, because 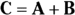 .
.
Tip: Another (and for some people, easier) way to do vector subtraction is to reverse the direction of the second vector (A in 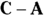 ) and use vector addition; that is, start with the first vector (C), put the reversed vector’s foot (A) at the first vector’s head, and draw the resultant vector.
) and use vector addition; that is, start with the first vector (C), put the reversed vector’s foot (A) at the first vector’s head, and draw the resultant vector.
Putting Vectors on the Grid
Vectors may look good as arrows floating in space, but that’s not exactly the most precise way of dealing with them. You can get numerical with vectors, taking them apart as you need them, by putting the arrows in a grid, on the coordinate plane. The coordinate plane allows you to work with vectors using (x, y) coordinates and algebra.
Adding vectors by adding coordinates
In this section, we explain how you can use the components of vectors to add vectors together. Doing so reduces the problem of adding vectors to a simple combination of adding numbers together, which is very useful when you solve problems.
Take a look at the vector addition problem 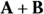 in Figure 4-6. Now that you have the vectors plotted on a graph, you can see how easy vector addition really is. If the measurements in Figure 4-6 are in meters, that means vector A is 5 meters to the right and 1 meter up, and vector B is 1 meter to the right and 4 meters up. To add them for the result, vector C, you add the horizontal parts together and the vertical parts together.
in Figure 4-6. Now that you have the vectors plotted on a graph, you can see how easy vector addition really is. If the measurements in Figure 4-6 are in meters, that means vector A is 5 meters to the right and 1 meter up, and vector B is 1 meter to the right and 4 meters up. To add them for the result, vector C, you add the horizontal parts together and the vertical parts together.
The resultant vector, C, ends up being 6 meters to the right and 5 meters up. You can see what that looks like in Figure 4-6: To get the horizontal part of the sum, you add the horizontal part of A (5 meters) to the horizontal part of B (1 meter). To get the vertical part of the sum, C, you just add the vertical part of A (1 meter) to the vertical part of B (4 meters).
Tip: If vector addition still seems cloudy, you can use a notation that was invented for vectors to help physicists and For Dummies readers keep it straight. Because A is 5 meters to the right (the positive x-axis direction) and 1 up (the positive y-axis direction), you can express it with (x, y) coordinates like this:
And because B is 1 meter to the right and 4 up, you can express it with (x, y) coordinates like this:
Having a notation is great, because it makes vector addition totally simple. To add two vectors together, you just add their x and y parts, respectively, to get the x and y parts of the result:
Remember: The whole secret of vector addition is breaking each vector up into its x and y parts and then adding those separately to get the resultant vector’s x and y parts. Nothing to it. Now you can get as numerical as you like, because you’re just adding or subtracting numbers. Getting those x and y parts can take a little work, but it’s a necessary step. And when you have those parts, you’re home free.
Example
Q. Assume you’re looking for a hotel that’s 20 miles due north and then 20 miles due east. What’s the vector that points at the hotel from your starting location?
A. The correct answer is (20, 20) miles.
- Say that the east direction is along the positive x-axis and that north is along the positive y-axis.
-
Write the problem in vector notation like this (east [positive x], north [positive y]):
Step 1: (0, 20) mi
Step 2: (20, 0) mi
-
Add these two vectors together by adding the coordinates:
The resultant vector is (20, 20) miles. It points from your starting point directly to the hotel.
Practice Questions
1. Suppose that you move to the right of the origin by 3.5 meters and then up 5.6 meters. What is your final vector from the origin, in vector component terms?
2. A marble starts at the origin and moves to the right 5.0 centimeters. What is its new displacement in vector component terms?
Practice Answers
1. (3.5, 5.6) m. You move to the right of the origin by 3.5 meters, leaving you at (3.5, 0) meters. Then you move up (in the positive y direction) by 5.6 meters, leaving you at (3.5, 5.6) meters.
2. (5.0, 0) cm. The marble moves to the right — in the positive x direction — by 5.0 centimeters, so its final location is (5.0, 0) centimeters.
Changing the length: Multiplying and dividing a vector by a number
You can perform simple vector multiplication by a scalar (number). If you multiply a vector by a scalar, say 5, then the vector gets five times longer. Each of the components will also be multiplied by 5. Division works the same way — just divide each of the components. Here’s an example and some practice problems to see how this works.
Example
Q. Say you’re driving along at 150 miles per hour eastward on a racetrack and you see a competitor in your rearview mirror. If you double your velocity, what is your final velocity in vector component form?
A. The correct answer is (300, 0) miles per hour. Your original velocity is (150, 0) miles per hour. Multiply each component by 2 to get your final velocity:
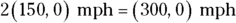
Practice Questions
1. What do you get if you divide the vector (3, –2) by 3?
2. What do you get if you multiply the vector (7, 3) by –1?
Practice Answers
1. (1, –2/3). Divide the components of the vector by 3:
2. (–7, –3). Multiply the components of the vector by –1:
A Little Trig: Breaking Up Vectors into Components
Physics problems have a way of not telling you what you want to know directly. As the preceding section explains, a vector can be described by its components, which are enough to uniquely specify a vector. Because a vector, by definition, is a quantity that has both magnitude and direction, another way to specify a vector is to use its magnitude and direction directly. If you know one way of describing the vector, you can work out the other.
These are just two different ways of specifying the same thing, and each has its own use in physics problems. Here’s why you may work with vector components:
- When you have vectors in components, they’re easy to add and subtract and manipulate generally. When a problem gives you vectors in terms of their magnitude and direction (which is often the case), you typically need to calculate their components just so you can work through the problem.
- Being able to treat the horizontal and vertical directions separately is useful because you can often split one difficult problem into two simple problems. Using components also helps when one direction is more important than the other. For example, a problem may say that a ball is rolling on a table at angle of 15° with a speed of 7.0 meters per second and ask you how long the ball will take to roll off the table’s edge if that edge is 1.0 meter away. In that case, you care only about how quickly the ball is moving horizontally, directly toward the table’s edge — the speed in the vertical direction doesn’t matter.
After you solve a problem, the answer usually needs to be in terms of the magnitude and direction. So after you find your answer in components, you often have to work out the magnitude and direction again.
This section shows you how you can take the magnitude and direction of a vector and work out its components as well as how you can take the components of a vector and work out its magnitude and direction.
Finding vector components
When you break a vector into its parts, those parts are called its components. For example, in the vector (4, 1), the x-axis (horizontal) component is 4, and the y-axis (vertical) component is 1. Typically, a physics problem gives you an angle and a magnitude to define a vector; you have to find the components yourself using a little trigonometry.
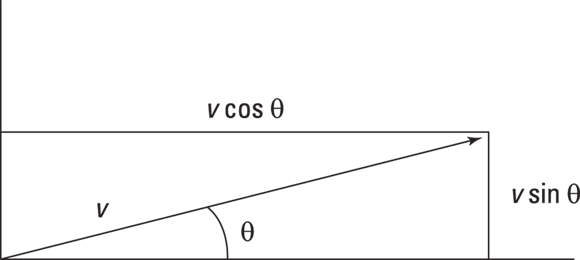
To see how to convert between the two ways of looking at vectors, take a look at vector v in Figure 4-7. The vector can be described as having a magnitude v at an angle of θ.
To convert this vector into the coordinate way of looking at vectors, you have to use the trigonometry shown in the figure. The x coordinate equals v cos θ, and the y coordinate equals v sin θ:
The two vector-component equations are worth knowing because you see them a lot in any beginning physics course. Make sure you know how they work, and always have them at your fingertips.
Of course, if you forget these equations, you can always retrieve them from basic trigonometry. You may remember that the sine and cosine of an angle in a right triangle are defined as the ratio of the opposite side and the adjacent side to the hypotenuse, like so: 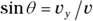 and
and 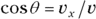 (see Chapter 2). By multiplying both sides of these equations by v, you can express the x and y components of the vector as
(see Chapter 2). By multiplying both sides of these equations by v, you can express the x and y components of the vector as
Example
Q. Suppose that you’ve walked away from the origin so you’re now 5.0 kilometers from the origin, at an angle of 45°. Resolve that into vector coordinates.
A. The correct answer is (3.5, 3.5) kilometers.
- Apply the equation vx = v cos θ to find the x coordinate. That’s 5.0 cos 45°, or 3.5.
- Apply the equation vy = v sin θ to find the y coordinate. That’s 5.0 sin 45°, or 3.5.
Practice Questions
1. Resolve a vector 9.0 meters long at 35° into its components.
2. Resolve a vector 4.0 meters long at 255° into its components.
Practice Answers
1. (7.4, 5.2) m. Apply the equation vx = v cos θ to find the x coordinate: 9.0·cos 35°, or 7.4. Then apply the equation vy = v sin θ to find the y coordinate: 9.0·sin 35°, or 5.2.
2. (–1.0, –3.9) m. Apply the equation vx = v cos θ to find the x coordinate: 4.0·cos 255°, or –1.0. Then apply the equation vy = v sin θ to find the y coordinate: 4.0·sin 255°, or –3.9.
Reassembling a vector from its components
Sometimes you have to find the angle and magnitude of a vector rather than the components. To find the magnitude, you use the Pythagorean theorem. And to find 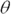 , you use the inverse tangent function (or inverse sine or cosine). This section shows you how these formulas work.
, you use the inverse tangent function (or inverse sine or cosine). This section shows you how these formulas work.
For example, assume you’re looking for a hotel that’s 20 miles due east and then 20 miles due north. From your present location, what is the angle (measured from east) of the direction to the hotel, and how far away is the hotel? You can write this problem in vector notation, like so (see the section “Putting Vectors on the Grid”):
- Step 1: (20, 0) miles
- Step 2: (0, 20) miles
When adding these vectors together, you get this result:
The resultant vector is (20, 20) miles. That’s one way of specifying a vector — use its components. But this problem isn’t asking for the results in terms of components. The question wants to know the angle and distance to the hotel. In other words, looking at Figure 4-8, the problem asks, “What’s h, and what’s 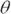 ?”
?”
Finding the magnitude
If you know a vector’s vertical and horizontal components, finding the vector’s magnitude isn’t so hard, because you just need to find the hypotenuse of a triangle. You can use the Pythagorean theorem 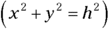 to solve for h:
to solve for h:
Plugging in the numbers gives you
Finding and checking the angle
Remember: When you know the horizontal and vertical components of a vector, you can use the tangent to find the angle because 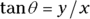 . All you have to do is take the inverse tangent of
. All you have to do is take the inverse tangent of 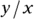 :
:
Suppose that you drive 20 miles east and 20 miles north. Here’s how you find 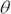 , the angle between your original position and your final one:
, the angle between your original position and your final one:
So the hotel is about 28 miles away (as you see from the earlier section “Finding the magnitude”) at an angle of 45°.
Warning: Be careful when doing calculations with inverse tangents, because angles that differ by 180° have the same tangent. When you take the inverse tangent, you may need to add or subtract 180° to get the actual angle you want. The inverse tangent button on your calculator will always give you an angle between 90° and –90°. If your angle isn’t in this range, you have to add or subtract 180°.
For this example, the answer of 45° must be correct. But consider a situation in which you’d need to add or subtract 180°: Suppose that you walk in completely the opposite direction to the hotel. You walk 20 miles west and 20 miles south (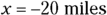 ,
, 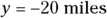 ), so if you use the same method to work out the angle, you get the following:
), so if you use the same method to work out the angle, you get the following:
You get the same answer for the angle even though you’re walking in completely the opposite direction as before! That’s because the tangents of angles that differ by 180° are equal. But if you look at the components of the vector (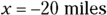 ,
, 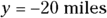 ), they’re both negative, so the angle must be between –180° and 0°. If you subtract 180° from your answer of 45°, you get –135°, which is your actual angle.
), they’re both negative, so the angle must be between –180° and 0°. If you subtract 180° from your answer of 45°, you get –135°, which is your actual angle.
An alternative method of working out the direction is to find the vector’s magnitude (hypotenuse) and then use the components in terms of the sine and cosine of the angle:
Then you can write the cosine and sine of the angle as
Now all you have to do is take the inverse cosine or sine:
Here are some practice questions on finding a vector’s magnitude and direction.
Example
Q. Convert the vector given by the coordinates (1.0, 5.0) into magnitude/angle format.
A. The correct answer is magnitude 5.1, angle 79°.
- Apply the Pythagorean theorem to find the magnitude. Plug in the numbers to get 5.1.
- Apply the equation θ = tan–1(y/x) to find the angle. Plug in the numbers to get tan–1(5.0/1.0) = 79°.
Practice Questions
1. Convert the vector (–1.0, 1.0) into magnitude/angle form.
2. Convert the vector (–5.0, –7.0) into magnitude/angle form.
Practice Answers
1. Magnitude 1.4, angle 135°. Apply the equation 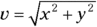 to find the magnitude, which is 1.4.
to find the magnitude, which is 1.4.
Apply the equation θ = tan–1(y/x) to find the angle: tan–1(1.0/–1.0) = –45°. However, note that the angle must really be between 90° and 180° because the first vector component is negative and the second is positive. That means you should add 180° to –45°, giving you 135° (the tangent of 135° is also 1.0/–1.0 = –1.0).
2. Magnitude 8.6, angle 234°. Apply the equation 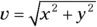 to find the magnitude, which is 8.6.
to find the magnitude, which is 8.6.
Apply the equation θ = tan–1(y/x) to find the angle: tan–1(–7.0/–5.0) = 54°. However, note that the angle must really be between 180° and 270° because both vector components are negative. That means you should add 180° to 54°, giving you 234° (the tangent of 234° is also –7.0/–5.0 = 7.0/5.0).
Adding vectors when you’re given magnitude and angle
You’re frequently asked to add vectors when solving physics problems. It’s easiest to add vectors together in component form, but often you’re given the magnitude and angle of the vectors instead. You just have to convert the vectors to component form, add the components, and convert back.
Example
Q. Add the two vectors in the following figure. One has a magnitude 5.0 and angle 45°, and the other has a magnitude 7.0 and angle 35°. State your answer in terms of magnitude and direction.
A. The correct answer is magnitude 12.0, angle 39°.
- Resolve the two vectors into their components. For the first vector, apply the equation vx = v cos θ to find the x coordinate. That’s 5.0 cos 45° = 3.5.
- Apply the equation vy = v sin θ to find the y coordinate of the first vector. That’s 5.0 sin 45°, or 3.5. So the first vector is (3.5, 3.5) in coordinate form.
- For the second vector, apply the equation vx = v cos θ to find the x coordinate. That’s 7.0 cos 35° = 5.7.
- Apply the equation vy = v sin θ to find the y coordinate of the second vector. That’s 7.0 sin 35° = 4.0. So the second vector is (5.7, 4.0) in coordinate form.
- To add the two vectors, add them in coordinate form: (3.5, 3.5) + (5.7, 4.0) = (9.2, 7.5).
- Convert (9.2, 7.5) into magnitude/angle form. Apply the equation θ = tan–1(y/x) to find the angle, which is tan–1(7.5/9.2) = tan–1(0.82) = 39°.
- Apply the equation
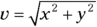 to find the magnitude, which is
to find the magnitude, which is 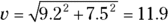 . Converting to two significant digits gives you 12.
. Converting to two significant digits gives you 12.
Practice Questions
1. Add a vector whose magnitude is 13.0 and angle is 27° to one whose magnitude is 11.0 and angle is 45°. State your answer in terms of magnitude and direction.
2. Add a vector whose magnitude is 10.0 and angle is 257° to one whose magnitude is 11.0 and angle is 105°. State your answer in terms of magnitude and direction.
Practice Answers
1. Magnitude 23.7, angle 35°. For the first vector, use the equation vx = v cos θ to find the x coordinate: 13.0·cos 27° = 11.6. Use the equation vy = v sin θ to find the y coordinate of the first vector: 13.0·sin 27°, or 5.90. So the first vector is (11.6, 5.90) in coordinate form.
For the second vector, use the equation vx = v cos θ to find the x coordinate: 11.0·cos 45° = 7.78. Use the equation vy = v sin θ to find the y coordinate of the second vector: 11.0·sin 45° = 7.78. So the second vector is (7.78, 7.78) in coordinate form.
Add the two vectors in coordinate form: (11.6, 5.90) + (7.78, 7.78) = (19.4, 13.7).
Convert (19.4, 13.7) into magnitude/angle form. Use the equation θ = tan–1(y/x) to find the angle: tan–1(13.7/19.4) = tan–1(0.71) = 35°.
Apply the equation 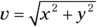 to find the magnitude, which is
to find the magnitude, which is 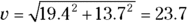 .
.
2. Magnitude 5.2, angle 170°. For the first vector, use the equation vx = v cos θ to find the x coordinate: 10.0·cos 257° = –2.25. Use the equation vy = v sin θ to find the y coordinate of the first vector: 10.0·sin 257°, or –9.74. So the first vector is (–2.25, –9.74) in coordinate form.
For the second vector, use the equation vx = v cos θ to find the x coordinate: 11.0·cos 105° = –2.85. Use the equation vy = v sin θ to find the y coordinate of the second vector: 11.0·sin 105° = 10.6. So the second vector is (–2.85, 10.6) in coordinate form.
Add the two vectors in coordinate form: (–2.25, –9.74) + (–2.85, 10.6) = (–5.10, 0.86).
Convert the vector (–5.10, 0.86) into magnitude/angle form. Use the equation θ = tan–1(y/x) to find the angle: tan–1(0.86/–5.10) = tan–1(–0.17) = 170°. Because x is negative and y is positive, this vector must be in the second quadrant.
Apply the equation 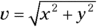 to find the magnitude, which is
to find the magnitude, which is 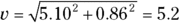 .
.
Featuring Displacement, Velocity, and Acceleration in 2-D
When an object is moving in only one dimension (as in Chapter 3), you only have to deal with one component, which is just a single number — displacement is just a distance, velocity is just a speed, and acceleration is just speeding up or slowing down. So in one dimension, vectors just look like numbers: The magnitude of the vector is the size of the number, and the direction of the vector is just the sign of the number.
However, displacement, velocity, and acceleration are always vectors. In the real world, an object may be moving in two or more dimensions, so direction is important. In this section, we take another look at the equations for motion, except in more than one dimension so you can see more clearly how the equations are really vector equations.
Displacement: Going the distance in two dimensions
Displacement, which is the change in position (see Chapter 3), has a magnitude and a direction associated with it. When you have a change of position in a particular direction and of a particular distance, then these are given by the magnitude and direction of the displacement vector.
Instead of writing displacement as s, you should write it as s, a vector (if you’re writing on paper, you can put an arrow over the s to signify its vector status). When you’re talking about displacement in the real world, direction is as important as distance.
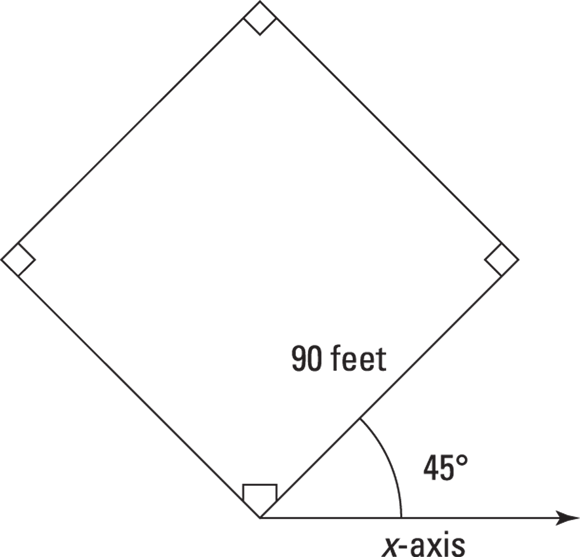
For example, say your dreams have come true: You’re a big-time baseball or softball hero, slugging another line drive into the outfield. You take off for first base, which is 90 feet away. But 90 feet in which direction? Because you know how vital physics is, you happen to know that first base is 90 feet away at a 45° angle, as you can see in Figure 4-9.
Now you’re set, all because you know that displacement is a vector. In this case, here’s the displacement vector:
What’s that in components?
Sometimes, working with angles and magnitudes isn’t as easy as working with x and y components. For example, say that you’re at the park and ask directions to the nearest bench. The person you ask is very precise and deliberate and answers, “Go north 10.0 meters.”
“North 10.0 meters,” you say. “Thanks.”
“Then east 20.0 meters. Then north another 50.0 meters.”
“Hmm,” you say. “North 10.0 meters, then 20.0 meters east, and then another 50.0 meters east … I mean north. Is that right?”
“Then 60.0 meters east.”
You look at the person warily. “Is that it?”
“That’s it,” she says. “Nearest bench.”
Okay, time for some physics. The first step is to translate all that north and east business into x and y coordinates like this: (x, y). So assuming that the positive x-axis points east and the positive y-axis points north (as on a map), the first step is 10.0 meters north, which becomes the following
That is, the first step is 10.0 meters north, which translates into 10.0 meters in the positive y direction. Adding the second step, 20.0 meters east (the positive x direction), gives you
The third step is 50.0 meters north, and adding that gives you
And, finally, the fourth step is 60.0 meters east, which gives you
Whew. Okay, what’s the sum of all these vectors? You just add up the components:
So the resulting vector is (80.0, 60.0) meters. Hmm, that seems a lot easier than the directions you got. Now you know what to do: Proceed 80.0 meters east and 60.0 meters north. See how easy adding vectors together is?
You can, if you like, go even further. You have the displacement to the nearest bench in terms of x and y components. But it looks like you’ll have to walk 80.0 meters east and then 60.0 meters north to find the bench. Wouldn’t it be easier if you just knew the direction to the bench and the total distance? Then you could cut the corner and just walk in a straight line directly to the bench.
This is an example where it’s good to know how to convert from the (x, y) coordinate form of a vector into the magnitude/angle form. And you can do it with all the physics knowledge you have. Converting (80.0, 60.0) meters to the magnitude/angle form allows you to cut the corner when you walk to the bench, saving a few steps.
You know that the x and y components of a vector form a right triangle and that the total magnitude of the vector is equal to the hypotenuse of the right triangle, h. So the magnitude of h is
Plugging in the numbers gives you the following:
Voilà! The bench is only 100 meters away. So instead of walking 80.0 meters east and then 60.0 meters north, a total distance of 140 meters, you need to walk only 100 meters. Your superior knowledge of vectors has saved you 40 meters.
But in what direction is the bench? You know it’s 100 meters away — but 100 meters which way? You find the angle from the x-axis with this trig:
So plugging in the numbers, you have
Therefore, the angle 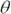 is the following (using the handy tan–1 button on your calculator):
is the following (using the handy tan–1 button on your calculator):
And there you have it — the nearest bench is 100 meters away at 36.9° from the x-axis. You start off confidently in a straight line at 36.9° from the east, surprising the person who gave you directions, who was expecting you to take off in the goofy zigzag path she’d given you.
Velocity: Speeding in a new direction
Velocity, which is the rate of change of position (or speed in a particular direction), is a vector. Imagine that you just hit a ground ball on the baseball diamond and you’re running along the first-base line, or the s vector, 90 feet at a 45° angle to the positive x-axis. But as you run, it occurs to you to ask, “Will my velocity enable me to evade the first baseman?” A good question, because the ball is on its way from the shortstop. Whipping out your calculator, you figure that you need 3.0 seconds to reach first base from home plate; so what’s your velocity? To find your velocity, you quickly divide the s vector by the time it takes to reach first base:
This expression represents a displacement vector divided by a time, and time is just a scalar. The result must be a vector, too. And it is velocity, or v:
Your velocity is 30 feet per second at 45°, and it’s a vector, v.
Remember: Dividing a vector by a scalar gives you a vector with potentially different units and the same direction.
In this case, you see that dividing a displacement vector, s, by a time gives you a velocity vector, v. It has the same magnitude as when you divided a distance by a time, but now you see a direction associated with it as well, because the displacement, s, is a vector. So you end up with a vector result rather than the scalars you see in Chapter 3.
Acceleration: Getting a new angle on changes in velocity
What happens when you swerve, whether in a car or on a walk? You accelerate in a particular direction. And just like displacement and velocity, acceleration, a, is a vector.
Remember: When you take into account the vector nature of acceleration, velocity and displacement, the equations from Chapter 3 become
Example
Q. You’re in a car traveling east at 88.0 meters per second; then you accelerate north at 5.00 meters per second2 for 10.0 seconds. What is your final speed?
A. The correct answer is 101 meters per second.
- Start with this vector equation:
- This equation is simply vector addition, so treat the quantities involved as vectors. That is, vi = (88, 0) meters per second and a = (0, 5) meters per second2. Here’s what the equation looks like when you plug in the numbers:
- Do the math:
- You’re asked to find the final speed, which is the magnitude of the velocity. Plug your numbers into the Pythagorean theorem.
- You can also find the final direction. Apply the equation θ = tan–1(y/x) to find the angle, which is tan–1(50.0/88.0) = tan–1(0.57) = 29.6° in this case.
Practice Questions
1. You’re going 40.0 meters per second east, and then you accelerate 10.0 meters per second2 north for 10.0 seconds. What are the direction and magnitude of your final velocity?
2. A car is driving along an icy road at 10.0 meters per second east when it skids, accelerating at 15 meters per second2 at 63° north of east for 1.0 second. What are the direction and magnitude of the car’s final velocity?
Practice Answers
1. Magnitude 108 m/s, angle 68° north of east. Start with this equation: 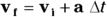 .
.
Plug in the numbers: vf = (40.0, 0) m/s + (0, 10.0 m/s2) (10.0 s) = (40.0, 100.0) m/s.
Convert the vector (40.0, 100.0) meters per second into magnitude/angle form. Use the equation θ = tan–1(y/x) to find the angle: tan–1(100.0/40.0) = tan–1(2.5) = 68°.
Apply the equation 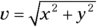 to find the speed — the magnitude of the velocity, giving you 108 meters per second.
to find the speed — the magnitude of the velocity, giving you 108 meters per second.
2. Magnitude 21.5 m/s, angle 39° north of east. Start with this equation: 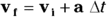 .
.
Convert the original velocity into vector component notation: (10.0, 0) meters per second.
Convert the acceleration into components. Use the equation ax = a cos θ to find the x coordinate of the acceleration: (15 m/s2)·cos 63° = 6.8 m/s2.
Use the equation ay = a sin θ to find the y coordinate of the acceleration: (15 m/s2)·sin 63°, or 13.4 m/s2. So the acceleration is (6.8, 13.4) m/s2 in coordinate form.
Perform the vector addition: (10.0, 0) m/s + (6.8 m/s2, 13.4 m/s2) (1.0 s) = (16.8 m/s, 13.4 m/s).
Convert the vector (16.8, 13.4) meters per second into magnitude/angle form. Use the equation θ = tan–1(y/x) to find the angle: tan–1(13.4/16.8) = tan–1(0.79) = 39°.
Apply the equation 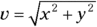 to find the magnitude of the velocity, giving you 21.5 meters per second.
to find the magnitude of the velocity, giving you 21.5 meters per second.
Accelerating Downward: Motion under the Influence of Gravity
Gravity problems present good examples of working with vectors in two dimensions. Because the acceleration due to gravity is only vertical, it’s especially useful to treat the horizontal and vertical components separately. Because there’s no acceleration in the horizontal direction, the horizontal component of motion is just uniform. The vertical component undergoes a constant acceleration of magnitude g, or 9.8 meters per second2, directed straight down. You can use this idea to make the solutions to trajectory problems really easy.
In this section, you sling projectiles around and let gravity do its work on shaping their trajectories. You’ll see that because the force of gravity only acts downward — that is, in the vertical direction — you can treat the vertical and horizontal components separately. We start with just vertical motion before going on to look at trajectories with both horizontal and vertical components to them. Armed with this information, you can calculate things like the time for a projectile to strike the ground or reach the top of its trajectory and the distance that a projectile will travel.
Shooting an object straight up
To start simply, figure out how far a projectile can travel straight up in the air. Say, for example, that on your birthday, your friends give you just what you’ve always wanted: a cannon. It has a muzzle velocity of 860 meters per second, and it shoots 10-kilogram cannonballs. Anxious to show you how it works, your friends shoot it off. The only problem: The cannon is pointing straight up. How long do you have to get out of the way?
Example
Q. The cannon has a muzzle velocity of 860 meters per second; the cannonballs have a mass of 10 kilograms each. What is the maximum height the cannonball will reach if you fire the cannon straight up (ignoring air resistance)?
A. The correct answer is 38 kilometers.
- Because the cannonball is moving straight up and down, use this equation:
- At the cannonball’s maximum height, its vertical velocity will be 0. The acceleration is 9.8 meters per second2 downward.
- Solve for s:
-
Plug in what you know — vf is 0 meters per second, vi is 860 meters per second, and the acceleration is g downward (g being 9.8 meters per second2, the acceleration due to gravity on the surface of the Earth), or –g:
The correct answer is about 38 kilometers. Notice that the mass of the cannonball does not affect the answer to this question.
Practice Questions
1. How long would it take a cannonball shot 28 kilometers straight up to reach its maximum height?
2. A firework explodes at the top of its trajectory at a height of 300 meters. If the firework was launched vertically, what was its initial velocity?
Practice Answers
1. 88 s. Use the following equation to find the time the cannonball will take to reach its maximum height:
The cannonball has velocity 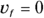 meters per second at the top and acceleration
meters per second at the top and acceleration 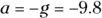 meters per second2. Solve for time:
meters per second2. Solve for time:
Enter the numbers into your calculator:
2. 80 m/s upward. The firework is moving straight up and down, so you use this equation:
At the firework’s maximum height, its vertical velocity will be 0. The acceleration is –g. Solve for vi:
Plug in what you know — vf is 0 meters per second, s is 300 meters, and the acceleration is g downward (g being 9.8 meters per second2, the acceleration due to gravity on the surface of the Earth), or –g:
Accounting for significant digits, the initial velocity is 80 meters per second upward.
Projectile motion: Firing an object at an angle
Firing projectiles at an angle introduces a horizontal component to the motion. However, the force of gravity acts only in the vertical direction, so the horizontal component of the trajectory is uniform. You can tackle this kind of problem by separating out the horizontal and vertical components of the motion.
Example
Q. One of your devious friends decides to fire a cannonball at an angle across a horizontal field, as shown in the following figure. Where will the cannonball land if the initial speed of the cannonball is 860 meters per second and it’s shot at an angle of 30° with respect to the horizontal?
A. The correct answer is 65 kilometers.
- Break the initial velocity into x and y components:
- The acceleration is –g in the y direction.
- Find the x and y components of the displacement:
- The cannonball hits the ground when y = 0. Solve the second equation to find the time:
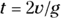 .
.
- Use the time to find the range of the cannon in the x direction:
-
Plug in numbers to find the range:
The correct answer is about 65 kilometers, accounting for significant digits.
Practice Questions
1. A pebble rolls horizontally off of a cliff with a speed of 4.3 meters per second. If the pebble falls 11 meters before hitting the ground, where does the pebble land?
2. You want to launch a water balloon at your friend who is 7.0 meters away. If you want the water balloon to start and end 1.0 meter above the ground and you throw the water balloon at an angle of 45°, how fast should you throw it to hit your friend?
Practice Answers
1. 6.4 m from the cliff. The initial velocity is in the x direction:
The acceleration is –g in the y direction.
Find the x and y components of the displacement:
Solve the second equation for time:
Plug into the x component of the displacement:
Plug into your calculator:
2. 8.4 m/s. Break the initial velocity into x and y components:
The acceleration is –g in the y direction.
Find the x and y components of the displacement:
The water balloon explodes when y = yi = 1 m. Solve the second equation to find the time: 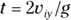 .
.
Use the time to find the range of the cannon in the x direction:
Solve for the initial speed:
Plug in numbers to find the initial speed:
 Mastering vector addition and subtraction
Mastering vector addition and subtraction Putting vectors into numerical coordinates
Putting vectors into numerical coordinates Dividing vectors into components
Dividing vectors into components Identifying displacement, acceleration, and velocity as vectors
Identifying displacement, acceleration, and velocity as vectors Understanding projectile motion
Understanding projectile motion
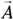 . The arrow means that this is not only a scalar value, which would be represented by A, but also something with direction.
. The arrow means that this is not only a scalar value, which would be represented by A, but also something with direction.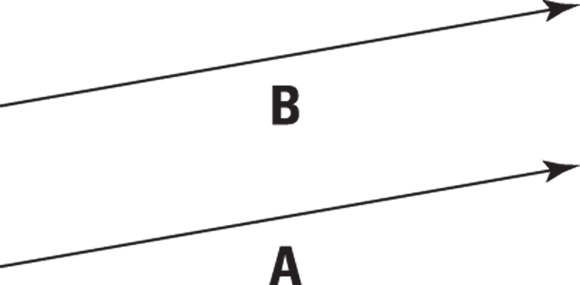

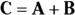 . The vector C is called the sum, the result, or the resultant vector.
. The vector C is called the sum, the result, or the resultant vector.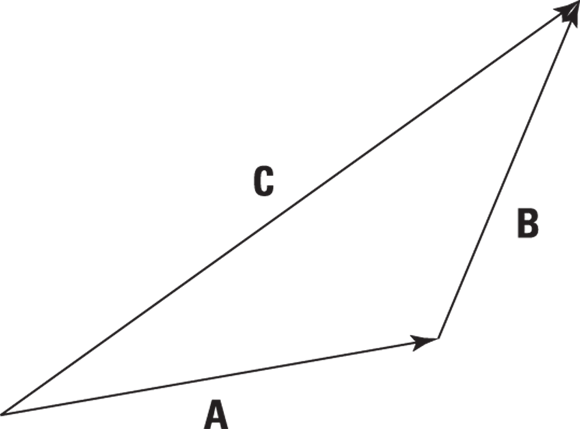
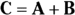 .
.
 ) and use vector addition; that is, start with the first vector (C), put the reversed vector’s foot (A) at the first vector’s head, and draw the resultant vector.
) and use vector addition; that is, start with the first vector (C), put the reversed vector’s foot (A) at the first vector’s head, and draw the resultant vector.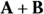 in
in 
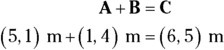
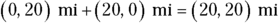
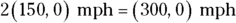
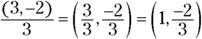
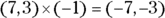
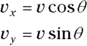
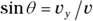 and
and 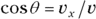 (see
(see 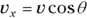
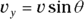
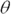 , you use the inverse tangent function (or inverse sine or cosine). This section shows you how these formulas work.
, you use the inverse tangent function (or inverse sine or cosine). This section shows you how these formulas work.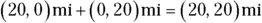
 ?”
?”
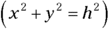 to solve for h:
to solve for h: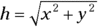
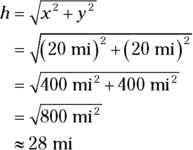
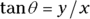 . All you have to do is take the inverse tangent of
. All you have to do is take the inverse tangent of 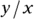 :
: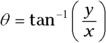
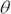 , the angle between your original position and your final one:
, the angle between your original position and your final one:
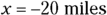 ,
, 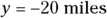 ), so if you use the same method to work out the angle, you get the following:
), so if you use the same method to work out the angle, you get the following: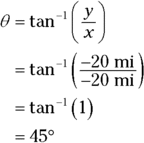
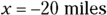 ,
, 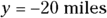 ), they’re both negative, so the angle must be between –180° and 0°. If you subtract 180° from your answer of 45°, you get –135°, which is your actual angle.
), they’re both negative, so the angle must be between –180° and 0°. If you subtract 180° from your answer of 45°, you get –135°, which is your actual angle.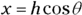
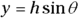
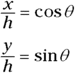
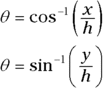
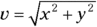 to find the magnitude, which is 1.4.
to find the magnitude, which is 1.4. to find the magnitude, which is 8.6.
to find the magnitude, which is 8.6.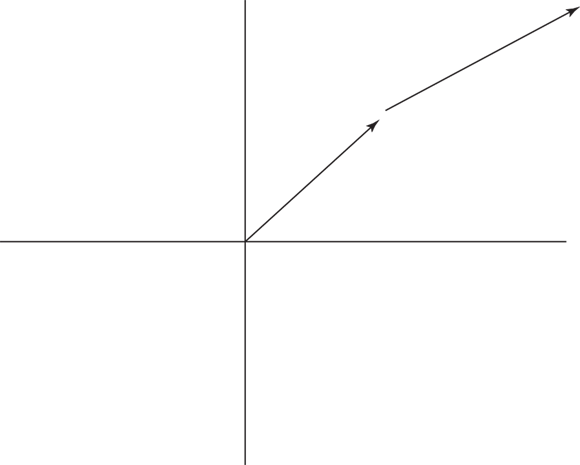
 to find the magnitude, which is
to find the magnitude, which is  . Converting to two significant digits gives you 12.
. Converting to two significant digits gives you 12.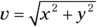 to find the magnitude, which is
to find the magnitude, which is 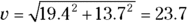 .
.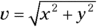 to find the magnitude, which is
to find the magnitude, which is 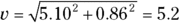 .
.
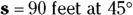

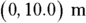

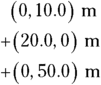
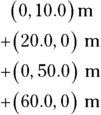

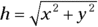

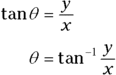
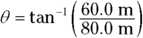
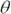 is the following (using the handy tan–1 button on your calculator):
is the following (using the handy tan–1 button on your calculator):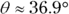
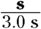
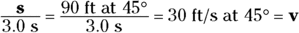
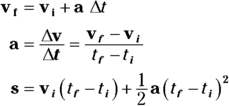
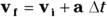
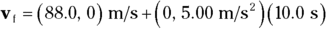
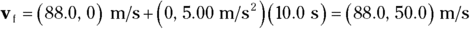
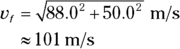
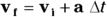 .
.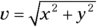 to find the speed — the magnitude of the velocity, giving you 108 meters per second.
to find the speed — the magnitude of the velocity, giving you 108 meters per second.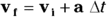 .
.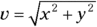 to find the magnitude of the velocity, giving you 21.5 meters per second.
to find the magnitude of the velocity, giving you 21.5 meters per second.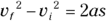
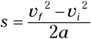

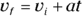
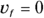 meters per second at the top and acceleration
meters per second at the top and acceleration 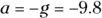 meters per second2. Solve for time:
meters per second2. Solve for time: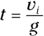

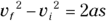
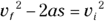


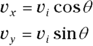
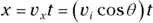
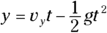
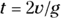 .
.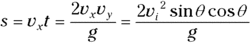
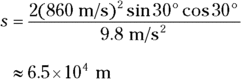
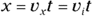
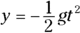
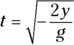
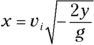
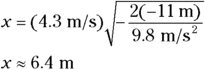
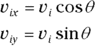
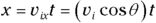
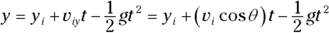
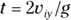 .
.