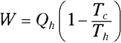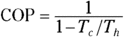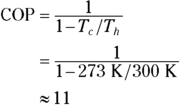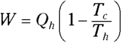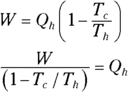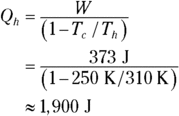Chapter 17
Heat and Work: The Laws of Thermodynamics
In This Chapter
 Achieving thermal equilibrium
Achieving thermal equilibrium
 Storing heat and energy under different conditions
Storing heat and energy under different conditions
 Revving up heat engines for efficiency
Revving up heat engines for efficiency
 Dropping close to absolute zero
Dropping close to absolute zero
If you’ve ever had an outdoor summer job, you know all about heat and work, a relationship encompassed by the term thermodynamics. This chapter brings together those two cherished topics, which we cover in detail in Chapter 9 (work) and Chapter 14 (heat).
Thermodynamics has laws one through three, much like Newton, but it does Newton one better: Thermodynamics also has a zeroth law. You may think that odd, because few other sets of everyday objects start off that way (“Watch out for that zeroth step — it’s a doozy …”), but you know how physicists love their traditions.
In this chapter, we cover thermal equilibrium (the zeroth law), heat and energy conservation (the first law), heat flow (the second law), and absolute zero (the third law). Time to throw the book at thermodynamics.
Thermal Equilibrium: Getting Temperature with the Zeroth Law
Two objects are in thermal equilibrium if heat can pass between them but no heat is actually doing so. For example, if you and the swimming pool you’re in are at the same temperature, no heat is flowing from you to it or from it to you (although the possibility is there). You’re in thermal equilibrium. On the other hand, if you jump into the pool in winter, cracking through the ice covering, you won’t be in thermal equilibrium with the water. And you don’t want to be. (Don’t try this physics experiment at home!)
To check for thermal equilibrium (especially in cases of frozen swimming pools that you’re about to jump into), you should use a thermometer. You can check the temperature of the pool with the thermometer and then check your temperature. If the two temperatures agree — in other words, if you’re in thermal equilibrium with the thermometer, and the thermometer is in thermal equilibrium with the pool — you’re in thermal equilibrium with the pool.
Remember: The zeroth law of thermodynamics says that if two objects are in thermal equilibrium with a third, then they’re in thermal equilibrium with each other. Then you can say that each of these objects has a thermal property that they all share — this property is called temperature.
Among other jobs, the zeroth law sets up the idea of temperature as an indicator of thermal equilibrium. The two objects mentioned in the zeroth law are in equilibrium with a third, giving you what you need to set up a scale such as the Kelvin scale.
Conserving Energy: The First Law of Thermodynamics
The first law of thermodynamics deals with energy conservation. One of the forms of energy involved is the internal energy that resides in the motion of the atoms and molecules (vibrations and random jostling). Another of the terms in this law is heat, which is a transfer of thermal energy. And finally, there is work, which is a transfer of mechanical energy; for example, work is done on a gas when it is compressed. The first law of thermodynamics states that these energies, together, are conserved. The initial internal energy in a system, Ui , changes to a final internal energy, Uf , when heat, Q, is absorbed or released by the system and the system does work, –W, on its surroundings (or the surroundings do work on the system), such that
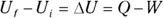
For mechanical energy to be conserved (see Chapter 9), you have to work with systems where no energy is lost to heat — there could be no friction, for example. All of that changes now. Now you can break down the total energy of a system, which includes heat, work, and the internal energy of the system.
These three quantities — heat, work, and internal energy — make up all the energy you need to consider. When you add heat, Q, to a system, and that system doesn’t do work, the amount of internal energy in the system, which is given by the symbol U, changes by Q. A system can also lose energy by doing work on its surroundings, such as when an engine lifts weight at the end of a cable. When a system does work on its surroundings and gives off no waste heat, its internal energy, U, changes by W. In other words, you’re in a position to think in terms of heat as energy, so when you take into account all three quantities — heat, work, and the internal energy — energy is conserved.
The first law of thermodynamics is a powerful one because it ties all the quantities together. If you know two of them, you can find the third.
Example
Q. Say that a motor does 1,000 joules of work on its surroundings while releasing 3,000 joules of heat. By how much does its internal energy change?
A. The correct answer is –4,000 joules.
- You know the motor does 1,000 joules of work on its surroundings, so you know its internal energy decreases by 1,000 joules.
- The motor also releases 3,000 joules of heat while doing its work, so the internal energy of the system decreases by an additional 3,000 joules. Think of negative values of work and heat as energy flowing out of the system, making the total change of internal energy this:
Practice Questions
1. You have a motor that absorbs 3,000 joules of heat while doing 2,000 joules of work. What is the change in the motor’s internal energy?
2. You have a motor that absorbs 2,500 joules of heat while doing 1,700 joules of work. What is the change in the motor’s internal energy?
Practice Answers
1. 1,000 J. Use this equation:
Plug in the numbers:
ΔU = 3,000 J [heat coming in] – 2,000 J [work going out] = 1,000 J
2. 800 J. Use this equation:
Plug in the numbers:
ΔU = 2,500 J [heat coming in] – 1,700 J [work going out] = 800 J
Working with gases
You come across a number of quantities in this chapter — volume, pressure, temperature, and so on. The ways in which these quantities vary as work is done determine the final state of the system. For example, if a gas is doing work while you keep its temperature constant, the amount of work performed and the intermediate and final states of the system will be different from when you keep the gas’s pressure constant instead.
Remember: A gas performs work only if the gas expands. You can show this idea mathematically. First, note that work, W, equals force, F, times distance, s (see Chapter 9):
In turn, force equals pressure, P, times area, A (see Chapter 8). This means that you can write work as pressure times area times distance:
Finally, the area times the distance (As) equals the change in volume, 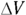 , so here’s the new work equation:
, so here’s the new work equation:
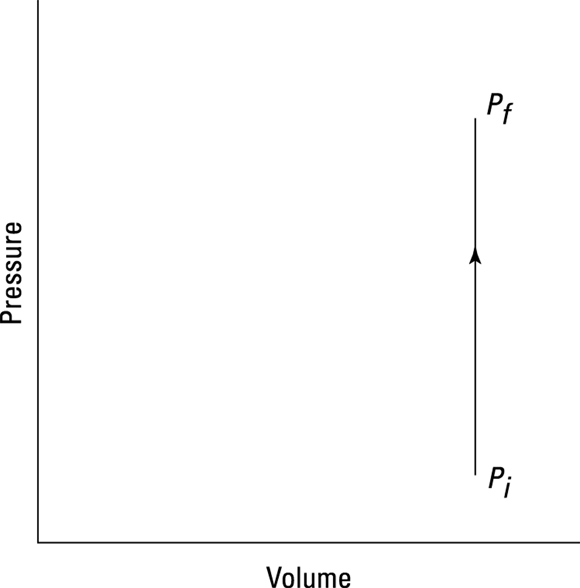
Tip: The formula 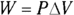 makes graphs of pressure versus volume very useful in thermodynamics. The curve you draw shows how pressure and volume change in relation to each other, and the area under the curve shows how much work is done.
makes graphs of pressure versus volume very useful in thermodynamics. The curve you draw shows how pressure and volume change in relation to each other, and the area under the curve shows how much work is done.
In the next four sections, we cover four standard conditions under which work is performed in thermodynamics: constant pressure, constant volume, constant temperature, and constant heat. We also graph pressure and volume for each of these processes and show you what work looks like. Note: When anything changes in these processes, the change is assumed to be quasi-static, which means the change comes slowly enough that the pressure and temperature are the same throughout the system’s volume.
At constant pressure: Isobaric processes
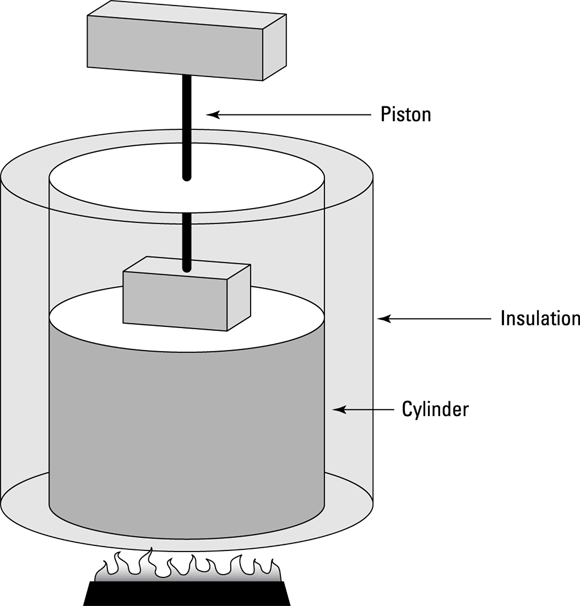
When you have a process where the pressure stays constant, it’s called isobaric (baric means “pressure”). In Figure 17-1, you see a cylinder with a piston being lifted by a quantity of gas as the gas gets hotter. The volume of the gas is changing, but the weighted piston keeps the pressure constant.
Graphically, you can see what the isobaric process looks like in Figure 17-2, where the volume is changing while the pressure stays constant. Because  , the work is the shaded area beneath the graph.
, the work is the shaded area beneath the graph.
Example
Q. You have 60.0 cubic meters of an ideal gas at 200.0 pascals and heat the gas until it expands to a volume of 120 cubic meters. How much work did the gas do?
A. The correct answer is 12,000 joules.
- Use this equation:
- Plug in the numbers:
The gas did 12,000 joules of work as it expanded under constant pressure.
Practice Questions
1. You have 50.0 cubic meters of an ideal gas at 1,000.0 pascals and heat the gas until it expands to a volume of 300.0 cubic meters. How much work did the gas do?
2. You have 100.0 cubic meters of an ideal gas at 300.0 pascals, and it expands, doing 6,000.0 joules of work. What is the final volume of the gas?
Practice Answers
1. 250,000 J. Use this equation:
Plug in the numbers:
2. 120 m3. Use this equation:
Solve for Vf :
Plug in the numbers:
At constant volume: Isochoric processes
What if the pressure in a system isn’t constant? You may see a simple closed container, which can’t change its volume. In this case, the volume is constant, so you have an isochoric process.
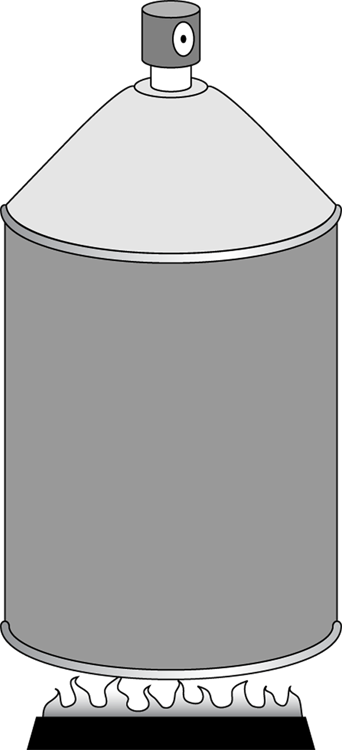
In Figure 17-3, someone has neglectfully tossed a spray can onto a fire. As the gas inside the spray can heats up, its pressure increases, but its volume stays the same (unless, of course, the can explodes).
How much work does the fire do on the spray can? Look at the graph in Figure 17-4. In this case, the volume is constant, so Fs (force times distance) equals 0. No work is being done — the area under the graph is 0.
Example
Q. You have 60.0 cubic meters of an ideal gas at 200.0 pascals and heat the gas until its pressure is 300.0 pascals at the same volume. How much work did the gas do?
A. The correct answer is none.
- Use this equation:
- Because ΔV = 0, no work was done. This process is an isochoric process.
Practice Questions
1. You have 50.0 cubic meters of an ideal gas at 1,000.0 pascals and heat the gas until it has a pressure of 3,000.0 pascals, still at the same volume. How much work did the gas do?
2. You have 300.0 cubic meters of an ideal gas at 1,500.0 pascals and heat the gas until it has a pressure of 6,000.0 pascals. How much work did the gas do if the volume is constant?
Practice Answers
1. 0 J. Use this equation:
Because no change in volume occurred, this process was isochoric, and no work was done.
2. 0 J. Use this equation:
Because no change in volume occurred, this process was isochoric, and no work was done.
At constant temperature: Isothermal processes
In an isothermal system, the temperature remains constant as other quantities change. Look at the remarkable apparatus in Figure 17-5. It’s specially designed to keep the temperature of the enclosed gas constant, even as the piston rises. When you apply heat to this system, the piston rises or lowers slowly in such a way as to keep the product of pressure times volume constant. Because  (see Chapter 14), the temperature stays constant as well. (Remember that n is the number of moles of gas that remains constant, and R is the gas constant.)
(see Chapter 14), the temperature stays constant as well. (Remember that n is the number of moles of gas that remains constant, and R is the gas constant.)
What does the work look like as the volume changes? Because 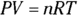 , the relation between P and V is
, the relation between P and V is
You can see this equation graphed in Figure 17-6, which shows the work done as the shaded area underneath the curve. But what the heck is that area?
Remember: The work done in an isothermal process is given by the following equation, where ln is the natural log (ln on your calculator), R is the gas constant (8.31 J/mol·K), Vf is the final volume, and Vi is the initial volume:
Remember: Because the temperature stays constant in an isothermal process and because the internal energy for an ideal gas equals 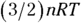 (see Chapter 16), the internal energy doesn’t change. Therefore, you find that heat equals the work done by the system:
(see Chapter 16), the internal energy doesn’t change. Therefore, you find that heat equals the work done by the system:
If you immerse the cylinder you see in Figure 17-5 in a heat bath, what would happen? The heat, Q, would flow into the apparatus, and because the temperature of the gas stays constant, all that heat would become work done by the system.
Example
Q. You have 1.0 mole of ideal gas at a constant temperature of 20°C, and you expand the gas from Vi = 0.010 cubic meters to Vf = 0.020 cubic meters. What work did the gas do in expanding?
A. The correct answer is 1,700 joules.
- Use this equation:
-
Plug in the numbers:
which rounds to 1,700 joules with significant figures.
- The work done by the gas was 1,700 joules. The change in the internal energy of the gas is 0 joules, as it must be in isothermal processes. Because Q = W, the amount the gas was heated is equal to 1,700 joules.
Practice Questions
1. You have 1.0 mole of ideal gas at a constant temperature of 30.0°C, and you expand the gas from Vi = 2.0 cubic meters to Vf = 3.0 cubic meters. What work did the gas do in expanding?
2. You have 0.60 mole of ideal gas at a constant temperature of 25°C, and you expand the gas from Vi = 1.0 cubic meters to Vf = 3.0 cubic meters. What heat was supplied to the gas in expanding?
Practice Answers
1. 1,020 J. Use this equation:
Plug in the numbers:
The work done by the gas was 1,020 joules. The change in the internal energy of the gas is 0 joules, as it must be in isothermal processes. Because Q = W, the heat added to the gas is equal to 1,020 joules.
2. 1,630 J. Use this equation:
Plug in the numbers:
The work done by the gas was 1,630 joules. The change in the internal energy of the gas is 0 joules, as it must be in isothermal processes. Because Q = W, the heat added to the gas is equal to 1,630 joules.
At constant heat: Adiabatic processes
In an adiabatic process, no heat flows from or to the system. Take a look at Figure 17-7, which shows a cylinder surrounded by an insulating material. The insulation prevents heat from flowing into or out of the system, so any change in the system is adiabatic.
Examining the work done during an adiabatic process, you can say  , so
, so 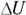 (the change in internal energy) equals –W. Because the internal energy of an ideal gas is
(the change in internal energy) equals –W. Because the internal energy of an ideal gas is 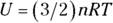 (see Chapter 14), the work done is the following:
(see Chapter 14), the work done is the following:
where Tf represents the final temperature and Ti represents the initial temperature. So if the gas does work, that work comes from a change in temperature — if the temperature goes down, the gas does work on its surroundings.
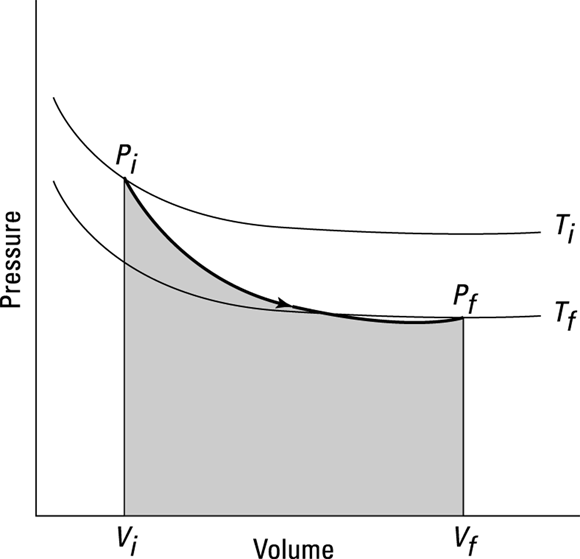
You can see what a graph of pressure versus volume looks like for an adiabatic process in Figure 17-8. The adiabatic curve in this figure, called an adiabat, is different from the isothermal curves, called isotherms. The work done when no heat flows into or out of the system is the shaded area under the curve.
In adiabatic expansion or compression, you can relate the initial pressure and volume to the final pressure and volume this way:
In this equation, 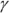 is the ratio of the specific heat capacity of an ideal gas at constant pressure divided by the specific heat capacity of an ideal gas at constant volume (specific heat capacity is the measure of how much heat an object can hold; see Chapter 15):
is the ratio of the specific heat capacity of an ideal gas at constant pressure divided by the specific heat capacity of an ideal gas at constant volume (specific heat capacity is the measure of how much heat an object can hold; see Chapter 15):
To figure out specific heat capacity, you need to relate heat, Q, and temperature, T. You usually use the formula 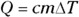 , where c represents specific heat capacity, m represents the mass, and
, where c represents specific heat capacity, m represents the mass, and 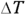 represents the change in temperature.
represents the change in temperature.
For gases, however, it’s easier to talk in terms of molar specific heat capacity, which is given by C and whose units are joules per mole-kelvin (J/mol·K). With molar specific heat capacity, you use a number of moles, n, rather than the mass, m:
To solve for C, you must account for two different quantities, CP (constant pressure) and CV (constant volume). Solved for Q, the first law of thermodynamics states that
So if you can get  and W in terms of T, you’re set.
and W in terms of T, you’re set.
First, consider heat at constant volume (QV ). The work done (W) is 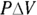 , so at constant volume, no work is done;
, so at constant volume, no work is done; 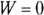 , so
, so 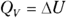 . And
. And 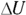 , the change in internal energy of an ideal gas, is
, the change in internal energy of an ideal gas, is 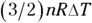 (see Chapter 16). Therefore, Q at constant volume is as follows:
(see Chapter 16). Therefore, Q at constant volume is as follows:
Now look at heat at constant pressure (QP). At constant pressure, work (W) equals 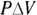 . And because
. And because 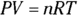 , you can represent the work as nRT:
, you can represent the work as nRT: 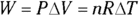 . At constant pressure, the change in energy,
. At constant pressure, the change in energy, 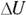 , is still
, is still  , just as it is at constant volume. Therefore, here’s Q at constant pressure:
, just as it is at constant volume. Therefore, here’s Q at constant pressure:
So how do you get the molar specific heat capacities from this? You’ve decided that  , which relates the heat exchange, Q, to the temperature difference,
, which relates the heat exchange, Q, to the temperature difference, 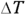 , via the molar specific heat capacity, C. This equation holds true for the heat exchange at constant volume, QV, so you write
, via the molar specific heat capacity, C. This equation holds true for the heat exchange at constant volume, QV, so you write
where CV is the specific heat capacity at constant volume. You already have an expression for QV, so you can substitute into the earlier equation:
Then you can divide both sides by 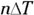 to get the specific heat capacity at constant volume:
to get the specific heat capacity at constant volume:
If you repeat this for the specific heat capacity at constant pressure, you get
Now you have the molar specific heat capacities of an ideal gas. The ratio you want, 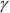 , is the ratio of these two equations:
, is the ratio of these two equations:
Remember: For an ideal gas, you can connect pressure and volume at any two points along an adiabatic curve this way:
Example
Q. You start with 3.0 liters of gas at 1.0 atmosphere and end up, after an adiabatic change, with 6.0 liters of gas. What is the new pressure?
A. The correct answer is 0.31 atmosphere.
- Use this equation:
- Plug in the numbers:
Practice Questions
1. You start with 1.0 liters of gas at 1.0 atmosphere and end up after an adiabatic change with 3.0 liters of gas. What is the new pressure?
2. You have 3.0 moles of ideal gas that undergo an adiabatic change, going from 23°C to 69°C. What work was done on the gas?
Practice Answers
1. 0.16 atmosphere. Use this equation:
Plug in the numbers:
2. 1,720 J. Use this equation:
Plug in the numbers:
The work done by the gas is –1,720 joules, so the work done on the gas is 1,720 joules.
Flowing from Hot to Cold: The Second Law of Thermodynamics
The second law of thermodynamics says that heat flows naturally from an object at a higher temperature to an object at a lower temperature, and heat doesn’t flow in the opposite direction of its own accord.
The law is certainly borne out in everyday observation — when was the last time you noticed an object getting colder than its surroundings unless another object was doing some kind of work? You can force heat to flow away from an object when it would naturally flow into it if you do some work — as with refrigerators or air conditioners — but heat doesn’t go in that direction by itself.
Heat engines: Putting heat to work
You have many ways to turn heat into work. You may have a steam engine, for example, that has a boiler and a set of pistons, or you may have an atomic reactor that generates superheated steam that can turn a turbine.
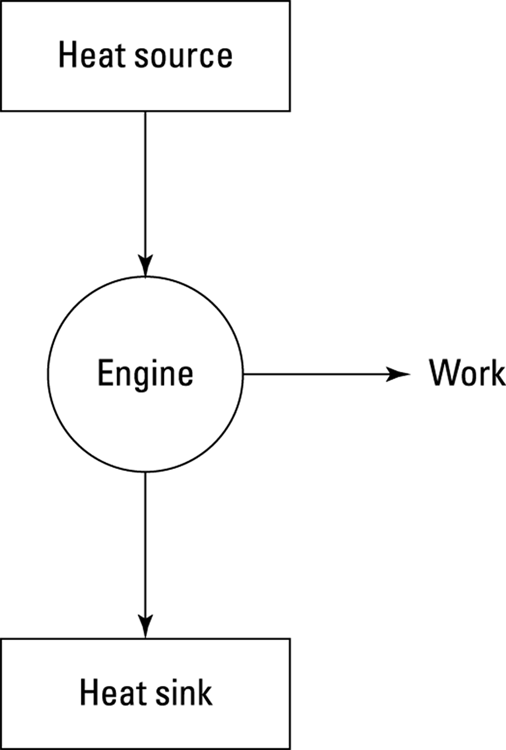
Engines that rely on a heat source to do work are called heat engines; you can see the principle behind a heat engine in Figure 17-9. A heat source provides heat to the engine, which does work. The waste heat left over goes to a heat sink, which effectively has an infinite heat capacity, because it can take such a large amount of heat energy without changing temperature. The heat sink could be the surrounding air, or it could be a water-filled radiator, for example. As long as the heat sink is at a lower temperature than the heat source, the heat engine can do work — at least theoretically.
Heat supplied by a heat source is given the symbol Q h (for the hot source), and heat sent to a heat sink is given the symbol Q c (for the cold heat sink). With some calculations, you can find the efficiency of a heat engine. The efficiency is the ratio of the work the engine does, W, to the input amount of heat — the fraction of the input heat that the engine converts to work:
If the engine converts all the input heat to work, the efficiency is 1.0. If no input heat is converted to work, the efficiency is 0.0. Often, the efficiency is given as a percentage, so you express these values as 100 percent and 0 percent.
Remember: Because total energy is conserved, the heat into the engine must equal the work done plus the heat sent to the heat sink, which means that 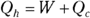 . Therefore, you can rewrite the efficiency in terms of just Qh and Qc:
. Therefore, you can rewrite the efficiency in terms of just Qh and Qc:
Example
Q. Your car is powered by a heat engine and does 3.0 × 107 joules of work getting you up a small hill. If the heat engine is 25 percent efficient, how much heat did it use, and how much did it exhaust?
A. The correct answer is 1.2 × 108 joules, 9 × 107 joules.
- Use this equation:
-
Solve for Qh:
So the input heat was 1.2 × 108 joules.
- Use this equation:
- Solve for Qc:
-
Plug in the numbers:
So the output heat was 9 × 107 joules.
Practice Questions
1. A car running on a heat engine does 7.0 × 107 joules of work. If the heat engine is 26 percent efficient, how much heat did it use, and how much did it exhaust?
2. An 87 percent efficient heat engine does 4.5 × 1010 joules of work. How much heat did it use, and how much did it exhaust?
3. A heat engine does 4.6 × 107 joules of work when supplied 8.9 × 107 joules. What is its efficiency?
4. A heat engine does 8.1 × 107 joules of work when supplied 10.9 × 107 joules. What is its efficiency?
Practice Answers
1. 2.7 × 108J, 2.0 × 108J.
Solve for Qh:
So the input heat was 2.7 × 108 joules.
Use this equation:
Solve for Qc:
Plug in the numbers:
So the output heat was 2.0 × 108 joules.
2. 5.2 × 1010J, 7 × 109J. Use this equation:
Solve for Qh:
So the input heat was 5.2 × 1010 joules.
Use this equation:
Solve for Qc:
Plug in the numbers:
So the output heat was 7 × 109 joules.
3. 52 percent. Use this equation:
Plug in the numbers:
4. 74 percent. Use this equation:
Plug in the numbers:
Limiting efficiency: Carnot says you can’t have it all
Given the amount of work a heat engine does and its efficiency, you can calculate how much heat goes in and how much comes out (along with a little help from the law of conservation of energy, which ties work, heat in, and heat out together). But why not create 100 percent efficient heat engines? Converting all the heat that goes into a heat engine into work would be nice, but the real world doesn’t work that way. Heat engines inevitably lose energy to their surroundings, such as through friction on the pistons in a steam engine.
Studying this problem, Sadi Carnot (a 19th-century engineer) came to the conclusion that the best you can do, effectively, is to use an engine that has no such losses. If the engine experiences no losses, the system will return to the state it was in before the process took place. This is called a reversible process. For example, if a heat engine loses energy overcoming friction, it doesn’t have a reversible process, because it doesn’t end up in the same state when the process is complete. You have the most efficient heat engine when the engine operates reversibly.
Carnot’s principle says that no nonreversible engine can be as efficient as a reversible engine and that all reversible engines that work between the same two temperatures have the same efficiency. Here’s the kicker: A perfectly reversible engine doesn’t exist, so Carnot came up with an ideal one.
No real engine can operate reversibly, so Carnot imagined a kind of ideal, reversible engine. In the Carnot engine, the heat that comes from the heat source is supplied at a constant temperature Th. Meanwhile, the rejected heat goes into the heat sink, which is at a constant temperature Tc. Because the heat source and the heat sink are always at the same temperature, you can say that the ratio of the heat provided and rejected is the same as the ratio of those temperatures (expressed in kelvins):
Remember: And because the efficiency of a heat engine is 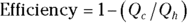 , the efficiency of a Carnot engine is
, the efficiency of a Carnot engine is
This equation represents the maximum possible efficiency of a heat engine. You can’t do any better than that. And as the third law of thermodynamics states (see the final section in this chapter), you can’t reach absolute zero; therefore, Tc is never 0, so the efficiency is always 1 minus some number. You can never have a 100 percent efficient heat engine.
Example
Q. Assume that you use the surface of the sun (about 5,778 kelvins) as the heat source and interstellar space (about 2.725 kelvins) as the heat sink for a Carnot heat engine. What is the engine’s efficiency?
A. The correct answer is 0.9995.
- Use this equation:
- Plug in the numbers:
Practice Questions
1. The heat source for a Carnot engine is at 87°C, and the heat sink is at 49°C. What is the engine’s efficiency?
2. The heat source for a Carnot engine is at 67°C, and the heat sink is at 29°C. What is the engine’s efficiency?
Practice Answers
1. 11%. Use this equation:
Plug in the numbers:
2. 11%. Use this equation:
Plug in the numbers:
Going against the flow with heat pumps
Usually, Carnot engines take heat from the hot reservoir (Q h), do work, and then dump the leftover heat in the cold reservoir (Q c). But what if you swapped the hot and cold reservoirs and actually did some work on the Carnot engine (instead of having it do work on you)? Then you could “pump heat uphill,” from the cold reservoir to the hot reservoir. You can do this if you connect the input of a Carnot engine to the cold reservoir and connect the exhaust to the hot reservoir.
Why on Earth would you want to move heat? Think about a cold room on an even colder day. If you connect a Carnot engine to the outside — which is colder than the inside — doing some work on the Carnot engine can drive heat into the room. This use of a Carnot engine is called a heat pump, because you put in work to drive heat uphill, from the cold reservoir to the hot one.
Why are heat pumps a good way to warm your house? Consider heating with electric heat instead. If you use enough electricity to add 1,000 joules to the heat inside your house, you have to pay for 1,000 joules of energy. But if you pump the heat from outside to inside, most of the heat comes from the cold reservoir, and you only have to provide the work needed to pump the heat into the hot reservoir.
A heat pump can be used to move heat in the other direction, too, to bring about cooling. In this case, mechanical work is used to pump heat from a source at a higher temperature to a lower temperature. Your refrigerator uses electrical energy to drive a compressor unit, which forms part of the refrigeration cycle.
Operating heat pumps requires less work than the heat they transfer. So how much work do you need to pump Qh of heat into the hot reservoir? You can start from this equation:
Here, Qc is the heat taken from the cold reservoir. W is the amount of work you need to supply to the heat pump. You’re trying to solve for the work, so rearrange the equation:
For a Carnot engine, 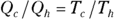 . Therefore, here’s the formula for the heat taken from the outside:
. Therefore, here’s the formula for the heat taken from the outside:
Now plug this value of Qc into the work equation 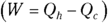 and simplify:
and simplify:
The heat delivered to you from a heat pump is more than the work you put into the heat pump. You can measure how much more heat you get out of a heat pump than the work you put in using the coefficient of performance (COP):
The coefficient of performance tells you how much heat you get out of a heat pump per work you have to put in to it.
For something like electric heat, where you have to pay for all the heat you get, the coefficient of performance is 1. But for a heat pump, the coefficient can be a lot higher than 1, indicating that you get more heat out of the pump than the work you put in.
The coefficient of performance depends on the inside and outside temperatures. You can put the coefficient of performance into a form that makes its dependence on temperature explicit.
Because 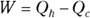 , the coefficient of performance equation becomes
, the coefficient of performance equation becomes
Or if you multiply both the numerator and denominator by 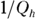 , you can express this like so:
, you can express this like so:
For a Carnot engine, 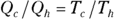 , so you end up with
, so you end up with
Example
Q. Suppose that you’re vacationing in your woodland cabin, which is at 20°C. You want to pump some heat in from outside, which is at 10°C. You decide you need about 4,000 joules of heat. How much work would you need to pump 4,000 joules into your house?
A. The correct answer is 136 joules.
- Use this equation:
- Plug in the numbers (with all temperatures in kelvins)
Practice Questions
1. The hot reservoir for a Carnot heat pump is at 27°C, and the cold reservoir is at 0.0°C. What is the heat pump’s coefficient of performance?
2. The hot reservoir for a Carnot heat pump is at 37°C, and the cold reservoir is at –23°C. How much heat can you pump using 373 joules of work?
Practice Answers
1. 11. Use this equation:
Plug in the numbers (with all temperatures in kelvins):
2. 1,900 J. Use this equation:
Solve for the heat Qh:
Plug in the numbers (with all temperatures in kelvins):
Going Cold: The Third (And Absolute Last) Law of Thermodynamics
Absolute zero is the lower limit for the temperature of any system, and the third law of thermodynamics can be formulated in terms of this temperature. The third law of thermodynamics is pretty straightforward — it just says that you can’t reach absolute zero (0 kelvins, or about –273.15°C) through any process that uses a finite number of steps. In other words, you can’t get down to absolute zero at all. Each step in the process of lowering an object’s temperature to absolute zero can get the temperature a little closer, but you can’t get all the way there.
 Achieving thermal equilibrium
Achieving thermal equilibrium Storing heat and energy under different conditions
Storing heat and energy under different conditions Revving up heat engines for efficiency
Revving up heat engines for efficiency Dropping close to absolute zero
Dropping close to absolute zero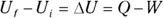
 is figuring out which signs to use. The quantity Q (heat transfer) is positive when the system absorbs heat and negative when the system releases heat. The quantity W (work) is positive when the system does work on its surroundings and negative when the surroundings do work on the system.
is figuring out which signs to use. The quantity Q (heat transfer) is positive when the system absorbs heat and negative when the system releases heat. The quantity W (work) is positive when the system does work on its surroundings and negative when the surroundings do work on the system.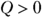 .
.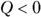 .
.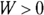 .
. .
.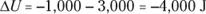
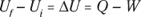

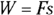
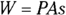
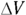 , so here’s the new work equation:
, so here’s the new work equation: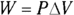
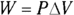 makes graphs of pressure versus volume very useful in thermodynamics. The curve you draw shows how pressure and volume change in relation to each other, and the area under the curve shows how much work is done.
makes graphs of pressure versus volume very useful in thermodynamics. The curve you draw shows how pressure and volume change in relation to each other, and the area under the curve shows how much work is done.
 , the work is the shaded area beneath the graph.
, the work is the shaded area beneath the graph.
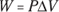
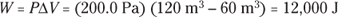
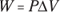

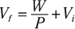

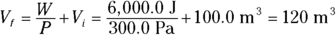
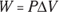

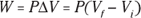
 (see
(see 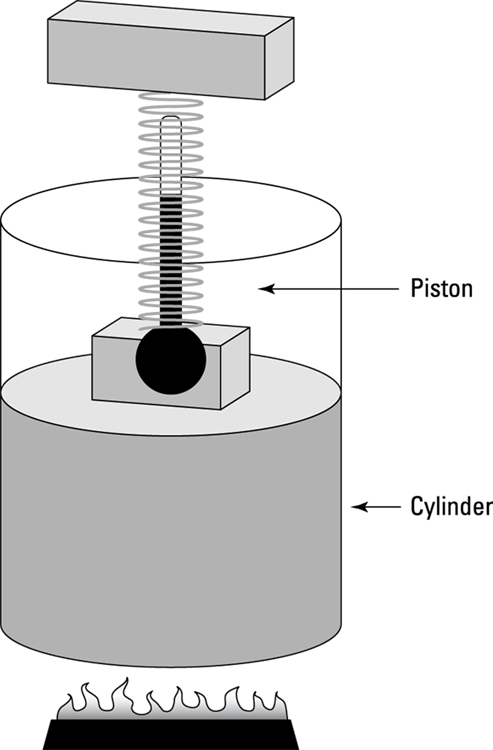
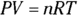 , the relation between P and V is
, the relation between P and V is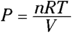

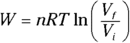
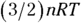 (see
(see 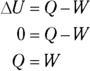
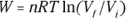

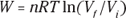


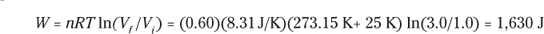
 , so
, so 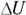 (the change in internal energy) equals –W. Because the internal energy of an ideal gas is
(the change in internal energy) equals –W. Because the internal energy of an ideal gas is 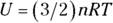 (see
(see 

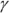 is the ratio of the specific heat capacity of an ideal gas at constant pressure divided by the specific heat capacity of an ideal gas at constant volume (specific heat capacity is the measure of how much heat an object can hold; see
is the ratio of the specific heat capacity of an ideal gas at constant pressure divided by the specific heat capacity of an ideal gas at constant volume (specific heat capacity is the measure of how much heat an object can hold; see 
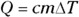 , where c represents specific heat capacity, m represents the mass, and
, where c represents specific heat capacity, m represents the mass, and 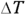 represents the change in temperature.
represents the change in temperature.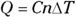

 and W in terms of T, you’re set.
and W in terms of T, you’re set.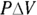 , so at constant volume, no work is done;
, so at constant volume, no work is done;  , so
, so 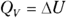 . And
. And 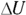 , the change in internal energy of an ideal gas, is
, the change in internal energy of an ideal gas, is 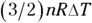 (see
(see 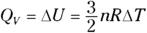
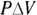 . And because
. And because 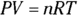 , you can represent the work as nRT:
, you can represent the work as nRT: 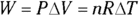 . At constant pressure, the change in energy,
. At constant pressure, the change in energy, 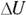 , is still
, is still  , just as it is at constant volume. Therefore, here’s Q at constant pressure:
, just as it is at constant volume. Therefore, here’s Q at constant pressure: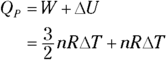
 , which relates the heat exchange, Q, to the temperature difference,
, which relates the heat exchange, Q, to the temperature difference, 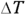 , via the molar specific heat capacity, C. This equation holds true for the heat exchange at constant volume, QV, so you write
, via the molar specific heat capacity, C. This equation holds true for the heat exchange at constant volume, QV, so you write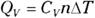
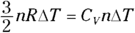
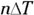 to get the specific heat capacity at constant volume:
to get the specific heat capacity at constant volume:

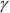 , is the ratio of these two equations:
, is the ratio of these two equations: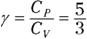
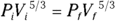
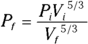
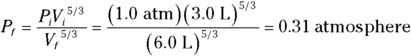

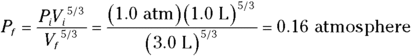
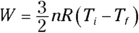
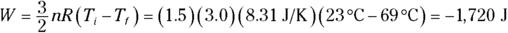

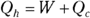 . Therefore, you can rewrite the efficiency in terms of just Qh and Qc:
. Therefore, you can rewrite the efficiency in terms of just Qh and Qc: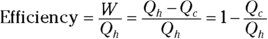


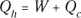
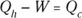
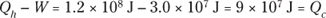
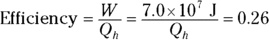

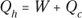
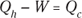
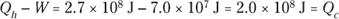
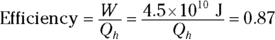
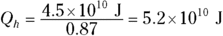
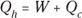


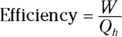

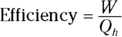

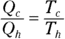
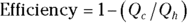 , the efficiency of a Carnot engine is
, the efficiency of a Carnot engine is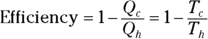
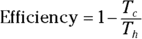
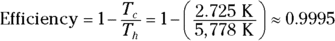
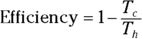
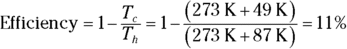

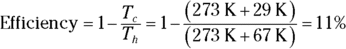

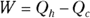
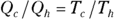 . Therefore, here’s the formula for the heat taken from the outside:
. Therefore, here’s the formula for the heat taken from the outside: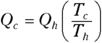
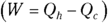 and simplify:
and simplify: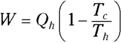
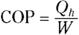
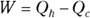 , the coefficient of performance equation becomes
, the coefficient of performance equation becomes
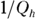 , you can express this like so:
, you can express this like so: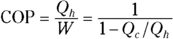
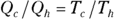 , so you end up with
, so you end up with