To understand why there are mountains high enough to keep me from getting to you, essentially why black holes are even ‘black’ in the first place, we first have to understand light itself. The history of our understanding of light is fascinating. Early philosophers, such as Euclid and Ptolemy, thought that our eyes themselves generated light, which then allowed us to see the world around us. Upon hearing this logic, Heron of Alexandria declared that if that was the case then the speed of light must be infinite and instantaneous, because as we open our eyes we see the light from stars at great distances instantly. We’re in the privileged position of hindsight here, knowing that our eyes don’t produce light but instead use our rod and cone cells to detect light, so we know this argument was flawed from the start. Yet the idea that the speed of light was infinite was still knocking around in the seventeenth century, with both Johannes Kepler and René Descartes (two giants of mathematics and astronomy) supporting the idea.

It was Galileo Galilei³² (of discovering Jupiter’s moons with his telescope fame in 1638) who was the first to actually try and measure the speed of light. His experiment consisted of two people on hilltops separated by one mile; one with a covered lantern which they would uncover and then record the exact time. The person on the other hilltop would then record the time at which they saw the light from the other person’s lantern. In Galileo’s experiment, the two people recorded the exact same time for the lantern being uncovered, and many philosophers at the time took that to mean that the speed of light must be infinite. But Galileo himself pointed out that the results of the experiment could also mean that light travelled too fast for a person a mile away to record a difference. He was right: it takes light just 0.000005 seconds to travel one mile, whereas an average human reaction time (i.e. your eyes detect light, send signals to your brain, your brain makes a decision and tells your muscles to react) is about 0.25 seconds.³³ To put that into context, it takes light less than that, about 0.133 seconds, to circumnavigate the Earth around the equator. So early scientists never really had a hope of measuring the speed of light on Earth, because the distances they used were just too short.

Having failed to put a number on the speed of light, Galileo gave up on that idea and turned his attention to another problem entirely: navigation. Galileo was living through the era of the first regular transatlantic voyages, and knowledge of how far north–south and east–west a ship was could make the difference between life and death.

Figuring out how far north or south you are – your latitude – is fairly easy. On the equator, the Sun at noon is directly overhead (at least on the equinoxes anyway, when the Earth isn’t tilted towards the Sun), but if you move further north or south, then the highest point that the Sun reaches in the sky drops. The angle it drops by is how far above the equator you’ve gone around the Earth. If only it were that simple all year round though, because the Earth’s axis is also tilted by 23°, which gives us our seasons. So there’s a little added complication, but essentially if you know roughly what time of year it is and you can measure the altitude of the Sun above the horizon at noon, then you can figure out how far north or south of the equator you are. Two fairly easy things to know and keep track of.

But what about figuring out your longitude – how far east or west you are? Today, a friendly airline pilot will usually tell you the local time as you land so that you can adjust your watch accordingly. Or by the magic of modern technology, your phone will automatically change to the right time zone. For example, landing in New York after flying from London, you’ll set your watch back by five hours after changing longitude by 75° to the west (that’s about 20 per cent of the way around the full 360° of the Earth, so about 20 per cent of a twenty-four hour day, which is 4.8 hours). Knowing your ‘time zone’ is therefore the key thing to working out your longitude, and in the seventeenth century, governments, kings and queens were all too aware of this.

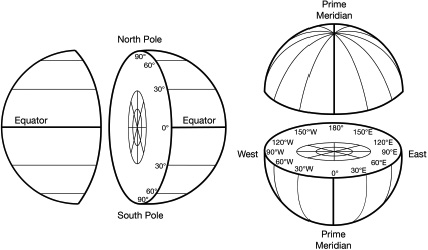
Latitude (left) and longitude (right) on Earth.

The problem was that they didn’t have any way of knowing the time in two separate places at once. Ideally, you’d set a watch to the time in Lisbon as you set off on your transatlantic voyage and watch how the Sun reached its peak at noon later and later every day according to that watch. Knowing the time difference between noon where you are and noon at the place you left gives you your ‘time zone’, and your longitude. But accurate mechanical clocks weren’t invented until the eighteenth century; in the seventeenth century sundials were the only means of telling the time, which only tell your local time with respect to the Sun, and not the time of the destination you left. Rewards were set up with big-money prizes by everyone from the British government to King Phillip III of Spain, in the hope that someone could crack the problem and work out a way to know the local time at sea.

It was Galileo and his precious moons of Jupiter that provided the first glimmer of hope. Just like our own Moon, which orbits the Earth every twenty-eight days like clockwork, Jupiter’s moons orbit with the same cosmic clock precision. The four largest ‘Galilean’ moons of Jupiter can be seen with a simple pair of modern binoculars (you need about 15x magnification) and it was these that Galileo meticulously observed, recording the time it took for each to make one orbit around Jupiter. A handy marker point was when each moon would disappear behind Jupiter and reappear on the other side, i.e. they were eclipsed by Jupiter from our perspective. These eclipses were incredibly predictable; the innermost moon, Io, orbits Jupiter every forty-two hours (just shy of two Earth days), and so giant spreadsheets could be made with predictions of the exact time in, say, Paris that Jupiter would eclipse Io.

Galileo’s idea was that if you could observe the time of the eclipse from wherever you were at sea and compare it to the predicted time of the eclipse in Paris’s time zone, then you’d be able to work out your longitude. He pitched this to the king of Spain in around 1616, and I can only imagine that the excitement was palpable. However, there were two problems. First, Galileo’s predictions weren’t accurate enough. If your estimate of how long it takes Io to orbit Jupiter is off by a few minutes, that error adds up very quickly over a few weeks, never mind the months that it would take to cross the Atlantic. Second, Galileo, ever the scientist and not a sailor, didn’t foresee the impracticalities of trying to observe Jupiter through a telescope on a ship that is at the mercy of the rolling sea. Unsurprisingly, the king of Spain was unwilling to award Galileo the cash prize.

So while Galileo’s method was quickly dismissed as impractical for sea voyages, it could still work on land, where map-makers were also clamouring for a more accurate way of determining longitude. They just needed more accurate predictions for the timings of the eclipses. In 1676, Ole Rømer and Giovanni Cassini swooped in to save the day. Rømer³⁴ was a Danish astronomer working at the Observatoire de Paris as Cassini’s assistant, where they picked up Galileo’s work and determined the timings between eclipses to a high degree of accuracy. The problem was that the number they measured kept changing from month to month. They noticed that the time between two eclipses got shorter and shorter as Earth travelled in its orbit around the Sun towards Jupiter, and got longer and longer as Earth moved in its orbit away from Jupiter.

The explanation that Cassini came up with was that the light from the eclipse had further to travel as Earth moved away from Jupiter, and therefore the speed of light was not infinite. Cassini announced this explanation to the scientific world in 1676, but was highly sceptical of it himself, and continued to raise other possibilities. Rømer, however, was a big supporter of the idea and set out to prove it by coming up with a way of predicting the eclipse timings for Io based on the relative positions of Earth and Jupiter. He focused on the geometry (rather than actually trying to measure the speed of light) and worked out that there’d be a delay to the eclipse depending on the angle between Jupiter and the Earth. The maximum delay was twenty-two minutes, when Earth and Jupiter were at their furthest distance from each other (an angle of 180°) and that reduced by the fraction of the angle as they got closer together.

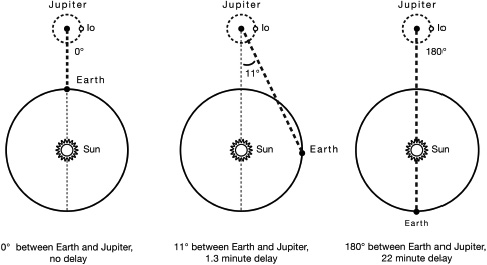
The delay in the timings of Io’s eclipses by Jupiter is due to the relative positions of Jupiter and Earth. If you know the angle between them, you can work out the delay due to the extra distance the light has to travel.

It took Rømer eight years of careful observations to work out this time delay, but it allowed for accurate predictions of the eclipse to calculate longitude. This is what Rømer cared about, not measuring the speed of light. While he believed his observations showed that the speed of light was not infinite, he never actually used them to calculate a value. Enter Christiaan Huygens, a Dutch astronomer who took Rømer’s data and used it to publish his Treatise on Light in 1690. In it, he made the jump from a maximum twenty-two-minute delay of Io’s eclipses, to light taking twenty-two minutes to travel the diameter of the Earth’s orbit around the Sun, a fact he said made one ‘acknowledge the extreme velocity of Light’.

The diameter of the Earth’s orbit wasn’t known absolutely at the time, it was only measured relative to the Earth’s diameter, and so Huygens quoted the speed of light as 16 ²⁄³ Earth diameters in one second (or more than 600,000 times greater than the speed of sound). That translates to 212,000,000 m/s. Huygens’ measurement was a bit short (due to the inaccuracies in the relative size of the Earth’s orbit to the size of the Earth); the modern value for the speed of light is 299,792,458 m/s,³⁵ so he was right to within an uncertainty of around 30 per cent. His measurement was a true milestone of scientific history, because it marked the first time that a universal constant (something that is the same across the entire Universe) was measured by humanity.

Of course, Huygens didn’t know that at the time, and neither did the multitudes of scientists who came after him who refined that measurement to greater accuracy over the next two centuries. It would take until the early twentieth century, with our old friend Albert Einstein, to understand why the speed of light was both universal and the finite speed limit of everything in the Universe. It all comes down to his most famous equation ever: E = mc² (‘E equals m c squared’), which if you remember from earlier means that energy and mass are equivalent – they are the same thing. But this is actually a simplified version of the full equation, for a specific case when objects aren’t moving. If something is moving, the full equation becomes:

E²=m²c⁴+pc²

p in this equation is the momentum. Momentum is essentially a measure of how much mass is in how much motion. The more momentum you have, the harder it is to stop your motion. For normal everyday objects, the momentum is mass multiplied by velocity (a speed with a direction, p = mv). So, normally, to increase momentum, and therefore the overall energy you have, you need to increase your speed. Which is fine for speeds on Earth: you put an extra bit of energy in and your speed goes up proportionally.

But Einstein’s equation above deals with ‘relativistic speeds’ – those close to the speed of light where strange things start to happen to your perception of time and space. Your momentum at these speeds is once again more complicated than for everyday speeds, so much so that as you approach the speed of light, your momentum no longer goes up proportionally. Instead, your momentum starts to exponentially increase. At 99.99 per cent of the speed of light, the momentum of an object is seventy times more than the value you’d expect it to be. At the speed of light, an object has an infinite amount of momentum.³⁶

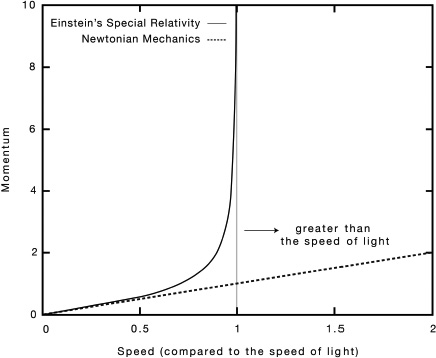
The difference in momentum for Einstein’s special relativity compared to everyday objects explained by Newtonian mechanics. It shows why you can never go faster than the speed of light because your momentum and energy tend to infinity.

This is true not just for momentum, but for all other properties, including the kinetic energy, or movement energy, of an object as it travels closer to the speed of light. And as E = mc² tells us, energy and mass are in principle the same thing. So if the energy of an object shoots up to infinity as it approaches the speed of light, then so too does its mass. So the faster you travel the heavier you get. As you approach the speed of light your mass approaches infinity. There is no number larger than infinity. When you’re travelling close to the speed of light, putting in more energy to try and go faster will increase your energy and mass, but not your speed. This is why nothing can go faster than the speed of light and it’s why 299,792,458 m/s is the ultimate speed limit across the entire Universe.

This limit on the speed of light is why black holes exist in the first place; it’s why they are ‘black’. If light speed was infinite, we’d be able to see what a black hole actually looked like, to where all that matter is squished and contained. Instead, light gets trapped in there because the escape velocity of the black hole is greater than the speed of light. All objects with mass in the Universe have escape velocities – the speed you’d need to travel to escape the pull of gravity from that object. Earth has an escape velocity, which is unfortunately much larger than the speed we can jump up at, or throw a ball up at, giving the age old adage: what goes up must come down. It’s why rockets need to burn an exorbitant amount of fuel to accelerate to a speed where they can fully escape the pull of Earth’s gravity, in order to power on out into the Solar System. The escape velocity depends on the mass of the object and how far away you are from the centre of that object; so on the Earth’s surface the escape velocity from Earth is around 11.2 km/s (thirty-three times the speed of sound), but on the Moon’s surface it’s much less, around 2.4 km/s.

For a black hole, there is nothing in the Universe that can travel faster than its escape velocity, not even light itself. It means that we will never observe what black holes truly look like, only their influence on objects around them due to their extreme gravity. But, so long as light doesn’t get too close to a black hole, its path through space can instead just get bent to the extreme, like the light from distant stars during a solar eclipse observed by Eddington, but turned up to eleven.

At that point, you can’t trust what your eyes are showing you any more, because the black hole has interfered with the light. In 2021, astronomers even detected light from behind a black hole. Imagine for a moment that I got into a spacecraft with this book and went around the far side of the Moon and hid where I couldn’t see Earth and you couldn’t see me. Imagine I cracked open this book to this page and shone a torch on it. Imagine that the Moon was so heavy that the light reflected off this page travelled on a curved path around the Moon and back to Earth so that you could still detect the light from it and read these words. That’s what a black hole can do: manipulate light to give you a glimpse of things you shouldn’t even be able to see.