Million to one odds happen eight times a day in New York.

—Penn Jillette

Do you remember the first season of Survivor that aired a few years back? Sixteen people were stranded on a deserted island and had to survive both their physical surroundings and social interactions. Every week, one person was voted off the island by the other members of the game, and the last person left was to receive one million dollars. In the final episode only two players, Kelly and Richard, remained. Their fate was determined by a vote of seven others who had already been eliminated. To help in their decision, the former members asked Kelly and Richard a number of questions, such as what three qualities they thought were most important to surviving the game. The results couldn't have been closer—after six votes were counted, the score was tied. The seventh and deciding vote gave Richard the million.

When the jury was asked why they voted the way they did, one of the members, Greg, said he couldn't decide, so he asked Kelly and Richard to pick a number between one and ten. Richard said seven and Kelly said three. Greg was thinking of the number nine and voted for the person who came the closest. After surviving thirty-nine days of physical, mental, and social challenges, the winner of the million-dollar prize was ultimately determined by chance! So it is in many aspects of our lives. We like to think that we can control our environment through our intellect and hard work. But the fact is, chance plays an important role in our everyday lives.

As Michael Shermer likes to say, we are causal-seeking animals.1 We have an innate desire to find patterns in our world. Throughout our evolution, people who discovered the causes for things survived and passed on their genes. For example, those early ancestors who saw that certain rocks could be chipped and formed into spearheads were more likely to be successful hunters. They were better able to hunt prey, feed their families, and produce offspring that would survive. This inherent tendency to seek out causes has usually served us well. However, our desire to find causes is so central to the way we think that we often see causes for things that are simply random events or the result of chance occurrences.

You're driving down the street thinking about your recently deceased Uncle Jim. Lost in thought, you're driving a little slower than usual. As you approach a busy intersection, a speeding car runs a stop sign on your right—you would have crashed if you were just two seconds earlier! Instead, you drive away safely, although a little rattled. Many people attribute supernatural or divine intervention to such an event. They say, “Uncle Jim was watching out for me—that's why I slowed down.” But we have to ask ourselves, does Jim's supernatural intervention offer the simplest explanation for the near miss? Remember Occam's razor—we should choose the explanation with the fewest assumptions. To accept the Jim hypothesis we have to assume that spirits of dead relatives exist, hang around this world, and watch out for our welfare—assumptions that have no hard evidence to support them. On the other hand, given the millions of cars on the road, probability theory predicts that there will be some accidents and some near misses. And so, a well-supported theory can explain the near miss without having to make untenable assumptions.

We naturally look for the reasons things happened the way they did. We want to believe that there's a reason for everything, and that if we understand what it is, we can, in some way, control the event. This even happens for the most obvious of chance events—the lottery. The lottery is certainly determined by chance, and yet, many people carefully choose their lottery numbers, thinking they can improve their odds. Entire books are written on the best way to choose winning numbers. In fact, studies show that people require more money to give up a lottery ticket if they pick their numbers than if they don't.2 We want to, and think we can, control chance events. However, before we attribute some underlying cause for an event, we should first ask ourselves if the event can be explained by the laws of chance. If the well-established rules of probability can explain an event, there may be no reason to attribute any other cause.

THE BELL CURVE

A while back I went to the casino with my friend Tom. As we walked by the gambling tables he said, “I've got a sure-fire way to win at Roulette.” When I asked him about the system he said, “Bet on either black or red, and if you win, take the money and make the same bet again. If you lose, double your bet on the next spin. Think about it. You can't lose too many times in a row—it's close to a 50/50 chance after taking out the house's edge—so you're bound to win fairly soon. And, when you finally win after a few losses, you'll recoup all of your prior losses and still win the current bet. You can't lose!” The system sounded great, so we pooled the meager resources we had at the time and went to the table with around $400. We put $5 on red and lost on the first spin. Undaunted, we doubled our bet and put $10 on red. Lost again. We then doubled the bet to $20 and lost a third time. Tom said, “We can't lose every time,” so we put $40 on red—and lost. Thinking it couldn't go on much longer, we put $80 on red, and lost. Finally, we put $160 down, and watched as the ball landed on black. Losing most of our money, we walked away in disgust.

Why doesn't this system always work? It seems like it should. To understand why, we have to realize that there are distributions for most things in this world. What do I mean by a distribution? Consider the height of all the males in the United States. There are many men around 5’8” to 6’, and fewer men above 6’8” or below 4’8”. If we were to graph the numbers of men in various height categories, we'd see a picture something like figure 4. This is a common shape for a distribution, and it's known as the bell curve. The midpoint of the distribution is quite high, indicating more people at that height, while the two ends tail off, indicating far fewer people with those heights. Distributions like the bell curve are significant when we think about chance because they illustrate that there are extreme observations, called outliers, for many different types of measurements. As a result, if you observe any single case, you can get an outlier by chance alone. If you select one male from the United States, he could be seven feet tall, or only four feet tall.

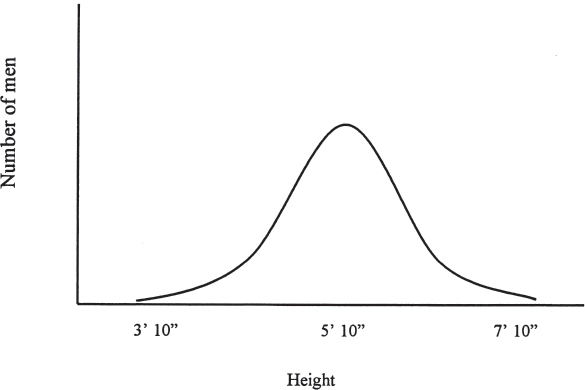
Figure 4. The bell curve: An example of a hypothetical height distribution of males in the United States.

What does this have to do with our miserable performance at the roulette table? Forgetting about the house's edge (the ball landing on 0 or 00), the probability of coming up red or black is similar to flipping a coin. If you flip a coin, the probability of getting a heads (or tails) is 0.5, because there are only two possible outcomes. What's the probability of getting two heads in a row? It's .5 × .5, or .25. That is, there's a 25% chance of getting two heads in a row. We can see this from the following list of possible outcomes, where H and T designates heads and tails:

HT, TH, HH, TT

Since there are four possible outcomes, HH has a one in four chance of occurring (25%). Now carry this reasoning to six flips. To calculate the probability of getting six consecutive heads, just multiply 0.5 by itself six times. The result is 1.56 percent. So, the probability of getting six heads in a row is roughly 1.5 percent for any set of six flips. While the probability is low, there are times when six coin flips will yield six heads. It's not as likely as, say, three heads and three tails, or four heads and two tails, but it can still occur for any given sequence of six flips. In fact, it's very likely to occur some of the time if we make a large number of six coin flips. For example, if we performed one thousand flip sequences, we would expect fifteen of them to be all heads by chance alone (1,000 x 1.5%). The same goes for the roulette wheel. With the thousands of spins on the roulette wheel, my friend Tom and I were just unlucky to be there when the ball landed on black six times in a row. Unfortunately, we lost our bankroll before a red number hit.

Since people think these extreme events are unlikely to occur, they frequently attribute some other, often mysterious, cause for the occurrences. They may think that the person flipping the coin or spinning the roulette wheel has some special power to control the outcome. However, before we attribute other possible causes, like psychic or mystical powers, for an event, we have to determine if those powers can make the event occur more than what we would expect from chance. As we saw, if we conducted one thousand six-coin flip sequences, we would expect around fifteen to be all heads from chance alone. Before we believe that someone's psychic power caused six heads in a row, it must be demonstrated that their power can yield significantly more than fifteen series of heads out of one thousand. If not, the six heads can be explained by chance.

The extreme occurrences that are evident in the tails of a distribution have led many people to form erroneous beliefs. Suppose your friend was just told he has a serious cancer, and that his average life expectancy is only one more year. When given such news, some patients try bizarre healing techniques, such as therapeutic touch, healing crystals, or even psychic surgery. Some of those patients may live longer than a year, and if they do, they often believe the alternative technique extended their life. But there's variability in the life span distribution—while the average life expectancy may be one year for a person with the cancer, some people may die after a month, while others may live for another five years. In essence, the tails of the distribution indicate that some people will live considerably longer than the average, a fact often ignored when forming beliefs.

The tails of a distribution are also a good reason to listen to the consensus of qualified experts rather than to a single individual. There are thousands of experts in most fields, and it's likely that some of them will believe some pretty weird things. There are outliers even among scientists, professors, and other qualified experts—something isn't true just because one expert says so. Remember the weird beliefs of John Mack from Harvard on alien abduction? If we look for the consensus view of the experts, we're more likely to get closer to the truth as we now know it.

Extrasensory Perception

Probability theory can explain many occurrences that, on the surface, seem inexplicable. Consider, for example, ESP. Michael Shermer went to Edgar Cayce's Association for Research and Enlightenment in Virginia Beach, an official-looking organization that conducts ESP experiments.3 When he arrived, they were running an experiment in which people (receivers) tried to discern certain shapes that another individual (a sender) was viewing. The “sender” concentrated on a card which displayed either a plus sign, square, star, circle, or wavy lines. At the same time, the “receivers” were told to concentrate on the sender's forehead and attempt to discern what he was thinking. Thirty-five people participated in the experiment, which ran two trials of twenty-five cards each.

The instructor said that everyone has ESP to some degree, although some have more than others. He indicated that, on average, people should correctly identify five out of twenty-five because of chance alone (since there were five symbols). In fact, he said that probability can explain any accuracy between three and seven. However, anyone who correctly identified more than seven symbols was said to have ESP. It turned out that three people identified eight symbols in the first trial, and one identified nine in the second trial. So, according to Cayce's association, at least four people participating in the experiment demonstrated ESP without even being trained. But did they really?

Probability theory indicates that there will be variation in the subjects' accuracies because of chance alone. While three people correctly guessed eight symbols in the first trial run, there were also three people who only got two right—the other twenty-nine correctly guessed between three and seven. In the second trial, there was one person who got nine right, but three people correctly guessed only two or one (all different people than those who scored low and high in the first set), and the rest were between three to seven. Remember the bell curve? These results look remarkably like a normal bell curve distribution that has an average of around five and some deviation around that average. So by chance alone, we would expect some people to get eight or nine right. In fact, with large groups of subjects we would expect some people to score even higher. The bottom line is, probability theory predicts these types of results, and so we don't need to invoke some mysterious cause like ESP.

According to Shermer, when he mentioned the bell curve to the group, the instructor said, “Are you an engineer or one of those statisticians or something?”4 The group laughed and the instructor went back to lecturing on how to improve their ESP. When we want to believe in something, we'll ignore, downplay, or even ridicule conflicting explanations. And, this is more likely to happen if we lack a good understanding of probability. In fact, researchers have found that people who believe in ESP do not understand probability as well as nonbelievers, and are therefore more likely to attribute paranormal explanations to extreme events.⁵

THE GAMBLERS' FALLACY

Let's go back to the roulette wheel. As you're watching the ball land on successive spins, you notice that it landed on black the last four times. If you had to put $100 on the next spin, would you put it on red, on black, or would you have no preference? Many people would choose red. Why? Because they think it's due. This is the gamblers' fallacy. If each spin is independent of the others, there's an equal chance the number will be red or black, irrespective of what happened on prior spins. But many people believe that what has recently occurred will affect what will occur next, even though the two events are independent. Every time I go to a casino I see seasoned gamblers falling prey to this fallacy, and losing their shirts because of it!6

The gambler's fallacy says that people will view independent events to be related in some way. In some cases, the fallacy leads people to believe that events will change, as in the case of the roulette wheel (red will come up next because black has come up a few times in a row). In other situations, however, people think that if an event has occurred, it's more likely to occur again. We can see this in the “hot hand.”

The Hot Hand

You're at a basketball game watching your hometown team play for the championship. It's the last quarter and your team is down, but they're making a comeback. In fact, your favorite player, Michael J., has just made three baskets in a row. People in the crowd start screaming, “Mike's hot—give the ball to Mike!” Why? It's common knowledge that basketball players get on a roll—they get hot. They get into a zone, and seem like they can't miss. Everybody's seen it happen. In fact, a survey of basketball fans showed that 91 percent thought a player was more likely to make a basket if he just made the last two or three shots, than if he missed the last two or three. Eighty-four percent thought the ball should be passed to a player who just made a couple of shots in a row.⁷

The problem is, there's no such thing as a hot hand. Psychologists Tom Gilovich, Robert Vallone, and Amos Tversky analyzed the shooting statistics for the Philadelphia 76ers and the Boston Celtics during the 1980–1981 season, and found absolutely no evidence to support the hot-hand theory.⁸ Streak shooting implies that the probability of making a basket, after having just made two or three baskets, is greater than the probability of making a basket after two or three misses. When you analyze the statistics, this just doesn't happen. For example, consider Dr. J. (Julius Irving), who typically took the most shots for the 76ers. The probability that Dr. J. would make a basket after having just made two baskets in a row was 52 percent, while the probability of his making a basket after two misses was 51 percent. If he made three baskets in a row, he sunk his next shot 48 percent of the time, while if he missed three baskets, he scored on his next shot 52 percent of the time. In short, the likelihood of him making a basket was around 50 percent, irrespective of what happened on his last few shots. Analyzing the free throws of the Boston Celtics revealed the same result. Larry Bird's chances of making a free throw were about the same (88 percent and 91 percent) whether he made the last free throw or not.

The data on a number of other players revealed similar findings. When Gilovich and his colleagues examined all the players on the 76ers, they found that the probability of a hit was actually a little lower after a hit than after a miss (average of 51 percent versus 54 percent over nine players). In addition, the probability of a hit following a hot period (three or four hits in the last four shots) was 50 percent, while a hit after a cold period (none or one hit in four shots) was 57 percent. They also analyzed the number of runs that the players had. A run is a sequence of consecutive hits or misses. For example, if X stands for a hit, and O a miss, the sequence XOOOXXO contains four runs. Streak shooting suggests that a player's hits cluster together, and so there should be fewer runs than what you would get from a random process. Only one player (Daryl Dawkins) deviated from chance, and he had more runs than expected, contrary to the hot-hand hypothesis. In fact, the analyses of twenty-three players on three different teams (the 76ers, New York Knicks, and New Jersey Nets) revealed similar results, even for players typically considered to be streak shooters, like Andrew Toney.

Gilovich and his colleagues then asked college players to shoot free throws and predict whether they would make the next basket given how they felt. According to the hot-hand theory, if they felt confident, like they were “in a zone,” they should be able to sink more shots. However, there was no association between the players' predictions and their actual performance. In essence, the data indicate that there is no hot hand in basketball. Remember, there are tails to any distribution, so by chance alone we would expect a player to occasionally hit a number of baskets in a row. It's not a hot hand, it's just the vagaries of chance. And yet, when players on the 76ers team were interviewed, all of them thought it was important to pass the ball to someone who had just made a few shots in a row.9

So why do we believe in streak shooting when successes and failures are statistically independent of one another? We misperceive random sequences. Consider, for example, the following problem:¹⁰

Which of the following sequences of Xs and Os seems more like it was generated by a random process (e.g., flipping a coin)?

_____XOXXXOOOOXOXXOOOXXXOX

_____XOXOXOOOXXOXOXOOXXXOX

Most people say the second is more random. However, the Xs and Os switch 70 percent of the time in the second case (they switch on fourteen of twenty possible alternations). On the other hand, the Xs and Os switch 50 percent of the time in the first case (ten out of twenty), which is similar to what you'd expect from a 50/50 chance sequence. And yet, 62 percent of people tested thought that the first case was similar to streak shooting.11 In effect, the first case is random, but looks streaky, while the second is not random, but is seen as such. If you said the second case looks random, you're expecting too many switches between the Xs and Os, which can lead you to see streaks in random processes. And if you see streaks in the randomness of the first case, you're likely to believe that a basketball player sometimes gets a hot hand.

Our intuitive ideas of randomness clearly don't coincide with the laws of chance. We tend to think that there shouldn't be a number of runs (e.g., a number of heads flipped or baskets made, in a row) because it doesn't seem random. However, if you flip a coin twenty times in a row, there is an 80 percent chance that at some point you'll get three heads or three tails in a row. There's a 50 percent chance you'll get four in a row, and a 25 percent chance you'll get a streak of five in a row.¹² Once again, our intuitive theories of the world can be erroneous, which is why we can't rely just on our experiences—we need systematic scientific inquiry.¹³

So what can we take away from all of this? On the one hand, we have probability theory and its well-established principles. To believe in the other, hotter hand, we would need to demonstrate that the baskets made deviate from what would be predicted by probability theory. Why? Occam's razor. If the events can already be explained by a well-established concept, we don't need another explanation, such as the hot hand. However, we are constantly on the lookout for the causes of things, and we don't appreciate the fact that many events in life are random. As a result, we start to attribute other causes for essentially random events.

COINCIDENCES

It is likely that unlikely things should happen.

—Aristotle

When I was in college one of my professors told our class about a long-shot meeting. He went on vacation to England during the summer, and, as he was walking down a street in London, he ran into one of the other professors in the department. You can imagine their surprise upon seeing one another, since they didn't tell each other they were going to vacation in England at that time. What are the chances of meeting someone you know on the streets of London during your vacation? Of all the places you can vacation, of all the times you can take your vacation, the odds are astronomically low. Isn't that proof there's something more going on?

When I was a doctoral student, I went to a casino night which the university was holding for charity. While driving to the affair, I happened to look down at the odometer and saw that my car had 55,555 miles on it. I said to myself, jokingly, “I guess five is my lucky number tonight.” As soon as I walked into the casino hall I went over to the Roulette wheel and put $5 on number five. It came out on the first spin, paying me thirty-five to one! Amazed, I took my winnings to the next roulette wheel, where I again put $5 on number five. Unbelievably, it again came out on the first spin, paying me thirty-five to one!

Coincidences can be quite astounding. A man by the name of George D. Bryson was traveling by train from St. Louis to New York. At the last minute, he decided to make a stop in Louisville, Kentucky, a city he'd never seen before. He asked for a hotel and was told to go to the Brown Hotel, where he registered and was given room 307. As a joke, he asked if he had any mail. The clerk handed him a letter addressed to Mr. George D. Bryson, Room 307. The prior occupant of room 307 was another George D. Bryson!14

Or consider this case: In 1914 a German mother photographed her son on a film plate, and then left the plate at a processor to be developed. World War I broke out and she couldn't return to the city to get the picture. Two years later, she bought a film plate in another city 200 miles away to take a picture of her new daughter. When the plate was developed, it was a double exposure—her daughter was superimposed over her son!15

Such events are astonishing, and can lead people to believe that something mysterious, mystical, or even divine is happening. In fact, stories like these led the psychologist Carl Jung to propose his concept of synchronicity. He maintained that such coincidences are the work of some unknown force trying to impose order on the events of the world. Once again, we have a case where someone, in this instance a very influential psychologist, is asserting that some mysterious force is the underlying cause. But let's apply Occam's razor. Is there a simpler explanation?

When thinking about coincidences such as these we shouldn't think in terms of the likelihood of these specific events happening. If we focus on the odds of my two professors meeting in London during their respective vacations, we'll likely conclude it's too low to be just a chance occurrence. But we shouldn't think about the meeting in that way. Yes, the odds of meeting that person, at that time, on the streets of London five thousand miles away from home, are extremely low. However, the odds that we meet someone we know, at some distant location, at some time in our life, are much greater. In fact, when you look at the millions and millions of people who travel every year, it's very likely that some of them will have chance meetings with someone they know. (Within one month, I saw, by coincidence, the same professor from our school at the Orlando, Florida, airport and again in a toy store in New York City.)

When thinking about the George D. Bryson coincidence, we shouldn't focus on the likelihood that the prior occupant of the room was another George D. Bryson. Instead, we should ask ourselves how likely it is that two successive occupants in some room in some hotel in some city at some point will have the same name.¹⁶ When thinking about my roulette winnings, don't focus on that one case. Think about the millions of people who place millions of bets on the roulette table. Given the sheer numbers, it's likely that some will win a few times in a row, even with their “lucky” numbers.

It seems incredible that such coincidences occur, and so we want to attribute them to otherworldly explanations. But given the billions and billions of events that occur every day, there are bound to be many such coincidences. In fact, it would actually be incomprehensible if coincidences didn't occur. For example, if we flipped five quarters, there's only a 3 percent chance of getting all heads. However, if we flipped these coins one hundred times, there's a 96 percent chance that one of those trials would give us all heads. As you can see, when we consider the vast number of events occurring, it's very likely that coincidences will occur. As Penn Jillette says, “Million to one odds happen eight times a day in New York.”17

However, many people still want to attribute mysterious causes to coincidences. A woman came up to Michael Shermer and said, “How do you explain coincidences like when I go to the phone to call my friend and she calls me? Isn't that an example of psychic communication?” Shermer replied, “No…it is an example of statistical coincidence. Let me ask you this: How many times did you go to the phone to call your friend and she did not call?” The woman later said she figured it out, she only remembers when it happens and forgets all the times it doesn't. Shermer said “You got it. It's just selective perception.” She replied, “No, this just proves that psychic power works sometimes but not others.” As James Randi said, believers in the paranormal are like “unsinkable rubber ducks.”¹⁸

SUPERSTITION

Wade Boggs was one of the most proficient hitters in the history of baseball. He won the batting title five times and had a lifetime batting average of .363. He is also highly superstitious. Early on in his career he formed the belief that he could hit better after eating chicken. For that reason, he ate chicken almost every day for twenty years when he played baseball. He is not alone in his superstitious behavior. Wayne Gretzky, the great hockey star, always tucked in the right side of his jersey behind his hip pads. Jim Kelly, the Buffalo Bills quarterback, forced himself to vomit before every game. Bjorn Borg did not shave after he began to play in a major tennis tournament. Bill Parcells would buy coffee from two different coffee shops before every game when he coached the New York Giants.¹⁹

Superstitious behavior is not confined to the sports arena. Like Wade Boggs, Michael Crichton, author of Jurassic Park, has the same thing for lunch every day when he's working on a new novel. One study found that between 20 to 33 percent of students rely on superstition and magic to bring good luck when taking exams. They wear special clothing, use certain pens, listen to lucky songs, knock on the exam room door, circle the building, or practice a number of other rituals.20 Some people believe that walking under a ladder or breaking a mirror will bring bad luck, and many fear the number thirteen. In fact, there's even a company in France that provides emergency dinner guests so that thirteen people never have to sit at the table together.²¹ And gamblers are notorious for exhibiting superstitious behavior.

A superstition is a belief that one thing affects something else, even though there is no logical relation between the two things. Superstitious behavior is often an outgrowth of coincidence. What happens? By coincidence, one event follows another, and a person then draws a causal association between the two events. For example, if a basketball player bounced a ball three times before attempting a crucial free throw, and then made the basket, he may associate the successful basket with the number of times the ball was bounced. In effect, the bouncing pattern was reinforced by the successful basket, resulting in a shooting ritual, a personal superstition.²² Wade Boggs most likely had one or two great batting days after he ate chicken, which launched his superstition. Superstitions caused by coincidences can be seen every day in casinos around the world. I've talked to many a gambler who are convinced that they have to put coins in a slot machine by hand, instead of using credits accumulated on the machine (which is much easier), in order to win. Why? They once had a big hit right after inserting coins by hand, and the coincidence created the superstition.

Linking superstitious beliefs and behaviors to coincidental events occurs because of a process that psychologists call operant conditioning. Psychologist B. F. Skinner, the foremost proponent of operant conditioning and author of the famous article “Superstition in the Pigeon,” convincingly demonstrated that coincidence develops superstitious behavior. Skinner put pigeons into separate cages and had a prize (food) dropped periodically (remarkably similar to slot machine payouts!). After just a few minutes, each bird exhibited a different bizarre behavior. Some bobbed their heads up and down, others walked in circles, while still others thrust their heads into different places in the cage. It turned out that the birds repeated the behaviors they performed just prior to receiving the food. Since they were doing different things just before food arrived, they developed different rituals. In essence, the pigeons' behavior was the result of a coincidence based on what they were doing when the food appeared. So it is with many human superstitions.23

While operant conditioning explains how many superstitions form, an underlying question remains: Why do they form? We live in a world of uncertainty. Many of life's events are unpredictable, and superstitions provide a way for many people to cope with the uncertainty. Superstitious behavior often makes us feel we have control over the situation; that, in some way, our behavior can affect the outcome. Consequently, superstitious behavior is likely to arise in situations that are more uncertain, random, and uncontrollable.

As we've seen, baseball and other sports figures are notorious for developing superstitions. Why? Uncertainty plays a big part in most sports. The best professional basketball players typically make only about half of their shots from the field. Quarterbacks in the NFL complete an average of about 58 percent of their passes. When such uncertainty exists, superstitions are bound to arise. This occurs even within a sport. If a baseball player gets a hit 30 percent of the time he is known as a premier batter, while hitting 26 percent makes him only average. In contrast, a fielder usually catches a ball that he's expected to catch, or throws a batter out, about 97 percent of the time. As a result, baseball superstitions tend to center most around hitting and pitching—many players feel less need for such superstitions when playing the field.²⁴

Our superstitious beliefs are often reinforced by a biased interpretation of future events. As noted earlier, many people think that things come in threes. To support that belief, they point to many instances where three bad or three good things happened over a period of time. However, evidence for such a superstition is problematic. Why? We remember the times that three things seemed to happen fairly close to one another, and forget all the times when three things didn't happen together. Once again, we remember the hits and forget the misses. Also, as we noted, there's never a time horizon stated. Do the three things have to happen within a week, a month, or a year? Sooner or later, three similar things are likely to occur. We can interpret just about any data as supporting the things-come-in-three superstition—if we wait long enough. As Stuart Vyse stated, “The fallibility of human reason is the greatest single source of superstitious belief.”25