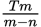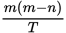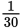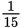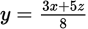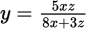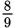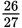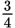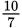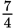Advanced Problem Solving Practice Set

  1. The numbers m, n, and T are all positive, and m > n. A weekend farm stand sells only peaches. On Saturday, the farm stand has T peaches to sell, at a profit of m cents each. Any peaches remaining for sale on Sunday will be marked down and sold at a profit of (m − n) cents each. If all peaches available for sale on Saturday morning are sold by Sunday evening, how many peaches, in terms of T, m, and n, does the stand need to sell on Saturday in order to make the same profit on each day?

  2. Set X consists of at least 2 members and is a set of consecutive odd integers with an average (arithmetic mean) of 37.

    Set Y consists of at least 10 members and is also a set of consecutive odd integers with an average (arithmetic mean) of 37.

    Set Z consists of all of the members of both set X and set Y.

    Which of the following statements must be true?

    1. The standard deviation of set Z is not equal to the standard deviation of set X.
    2. The standard deviation of set Z is equal to the standard deviation of set Y.
    3. The average (arithmetic mean) of set Z is 37.
    1. I only
    2. II only
    3. III only
    4. I and III
    5. II and III

  3. The number 10,010 has how many positive integer factors?

    1. 31
    2. 32
    3. 33
    4. 34
    5. 35

  4. A department of motor vehicles asks visitors to draw numbered tickets from a dispenser so that they can be served in order by number. Six friends have graduated from truck-driving school and go to the department to get commercial driving licenses. They draw tickets and find that their numbers are a set of evenly spaced integers with a range of 10. Which of the following could NOT be the sum of their numbers?

    1. 1,254
    2. 1,428
    3. 3,972
    4. 4,316
    5. 8,010

  5. For all values of x, y, and z, x ◊ y ◊ z = x2(y − 1)(z + 2).

    If a < 0, which of the following shows R, S, and T arranged in order from least to greatest?

    R: 1 ◊ a ◊ 3

    S: 3 ◊ a ◊ 1

    T: a ◊ 3 ◊ 1

    1. R, S, T
    2. T, S, R
    3. R, T, S
    4. T, R, S
    5. S, R, T

  6. If a and b are integers, and 2a + b = 17, then 8a + b cannot equal which of the following?

    1. −1
    2. 33
    3. 35
    4. 65
    5. 71

  7. Two workers have different pay scales. Worker A receives $50 for any day worked plus $15 per hour. Worker B receives $27 per hour. Both workers may work for a fraction of an hour and be paid in proportion to their respective hourly rates. If Worker A arrives at 9:21 a.m. and receives the $50 upon arrival and Worker B arrives at 10:09 a.m., assuming both work continuously, at what time would their earnings be identical?

    1. 11:09 a.m.
    2. 12:01 p.m.
    3. 2:31 p.m.
    4. 3:19 p.m.
    5. 3:36 p.m.
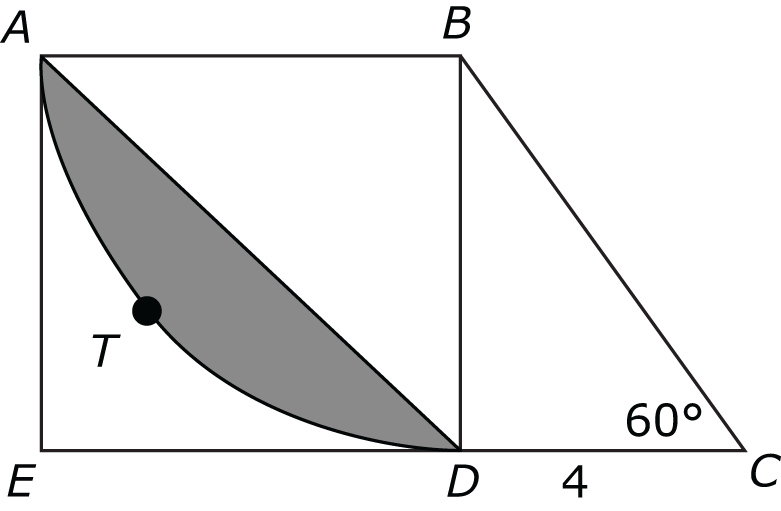
  8. One side of square ABDE is also a leg of triangle BDC. The other leg of triangle BDC is measure 4, and angle C, which is opposite BD, is meausre 60 degrees. A diagonal AD bisects the square, and arc ATD defines a shaded area bounded by the arc and the diagonal AD.

    In the figure above, ABDE is a square, and arc ATD is part of a circle with center B. The measure of angle BCD is 60°, and line segment CD has a length of 4. What is the area of the shaded region?

    1. 16π − 32
    2. 12π − 24
    3. 12π − 48
    4. 48π − 24
    5. 48π − 48

  9. When the cube of a non-zero number y is subtracted from 35, the result is equal to the result of dividing 216 by the cube of that number y. What is the sum of all the possible values of y?

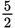
    2. 5
    3. 6
    4. 10
    5. 12

  10. One letter is selected at random from the five letters V, W, X, Y, and Z, and event A is the event that the letter V is selected. A fair six-sided die with sides numbered 1, 2, 3, 4, 5, and 6 is to be rolled, and event B is the event that a 5 or a 6 shows. A fair coin is to be tossed, and event C is the event that a head shows. What is the probability that event A occurs and at least one of the events B and C occurs?

  11. A car traveled from Town A to Town B. The car traveled the first of the distance from Town A to Town B at an average speed of x miles per hour, where x > 0. The car traveled the remaining distance at an average speed of y miles per hour, where y > 0. The car traveled the entire distance from Town A to Town B at an average speed of z miles per hour. Which of the following equations gives y in terms of x and z?

  12. An ornithologist has studied a particular population of starlings and discovered that their population has increased by 400 percent every 10 years starting in 1890. If the initial population in 1890 was 256 birds, how large was the population of starlings in 1970?

    1. 102,400
    2. 10,000,000
    3. 16,777,216
    4. 20,000,000
    5. 100,000,000

  13. If (x2 + 8)yz < 0, wz > 0, and xyz < 0, then which of the following must be true?

    1. x < 0
    2. wy < 0
    3. yz < 0
    1. II only
    2. III only
    3. I and III only
    4. II and III only
    5. I, II, and III

  14. If 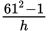is an integer, then h could be divisible by each of the following EXCEPT

    1. 8
    2. 12
    3. 15
    4. 18
    5. 31

  15. If a, b, and c are integers such that 0 < a < b < c, and a is even, b is prime, and c is odd, which of the following is a possible value for abc?

    1. 5
    2. 12
    3. 16
    4. 34
    5. 54

  16. A fair die with sides numbered 1, 2, 3, 4, 5, and 6 is to be rolled 4 times. What is the probability that on at least one roll, the number showing will be less than 3?

  17. There are 816 students enrolled at a certain high school. Each of these students is taking at least one of the subjects economics, geography, and biology. The sum of the number of students taking exactly one of these subjects and the number of students taking all three of these subjects is 5 times the number of students taking exactly two of these subjects. The ratio of the number of students taking only the two subjects economics and geography to the number of students taking only the two subjects economics and biology to the number of students taking only the two subjects geography and biology is 3:6:8. How many of the students enrolled at this high school are taking only the two subjects geography and biology?

    1. 35
    2. 42
    3. 64
    4. 136
    5. 240

  18. Working alone at a constant rate, Machine P produces a widgets in 3 hours. Working alone at a constant rate, Machine Q produces b widgets in 4 hours. If Machines P and Q work together for c hours, then in terms of a, b, and c, how many widgets will Machines P and Q produce?

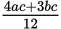
    4. 4ac + 3bc
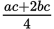
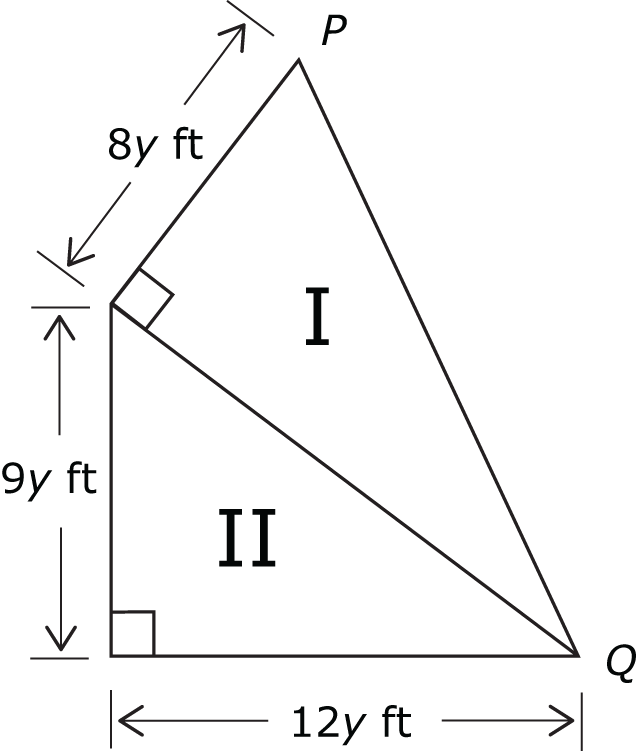
  19. Triangle 1 has a leg of 8y feet and a hypotenuse labeled PQ. The other leg is the hypotenuse of triangle 2. This triangle has legs of 9y feet and 12y feet.

    In the figure above, the perimeter of triangle I is 16 feet greater than the perimeter of triangle II. What is the length of PQ, in feet?

    1. 27
    2. 51
    3. 68
    4. 75
    5. 85

  20. If x > 0, y > 0, and , what is the value of ?