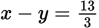Special Cases in Systems of Linear Equations

Learning Objective

In this section, you will learn how to: 

• Identify cases in which it may not be necessary to have as many equations as variables in a system of equations

On the GMAT, it is not always necessary to solve for each variable to answer a question. Some questions will ask you to solve for a sum, difference, or other relationship between variables rather than for the variables themselves. In such a case, rather than attempting to solve for both x and y, you will solve for values for expressions such as (x + y) or (x − y), the average of x and y, or the ratio between the two variables. Questions involving special cases reward test takers who seek out opportunities to use Critical Thinking and Pattern Recognition in GMAT questions.

Special cases in systems of linear equations appear most frequently in problems involving sums, differences, averages, and ratios. You will see them appear more often in Data Sufficiency questions than in Problem Solving questions, because Data Sufficiency questions require you to recognize whether you have enough information to determine a relationship. Don’t assume that you can’t answer a question just because there are more variables present than there are equations. By simplifying the equation, you may be able to cancel out one or more variables entirely.

In-Format Question: Special Cases in Systems of Linear Equations on the GMAT

Let’s look at a Data Sufficiency question that involves special cases in systems of linear equations.

1. What is the value of x − y?
   1. 3x + 3y = 31
   2. 3x − 3y = 13

Step 1: Analyze the Question Stem

First, look at your question stem and recognize that this is a special situation. You are not asked for the value of x or y; rather, you are asked for the value of x − y. Next, determine whether there is enough information to find the value of x − y. Keep in mind that you do not have to know the values of each of the variables x and y to be able to find the value of x − y. Because the question stem does not provide any information for finding the value of x − y, look at the statements.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) is 3x + 3y = 31. There is no way to rearrange this equation to find the value of x − y. Therefore, Statement (1) is insufficient. You can eliminate (A) and (D).

Statement (2) is 3x − 3y = 13. Factoring 3 from the left side of this equation, you have 3(x − y) = 13. Dividing both sides of this equation by 3, you have 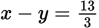, and Statement (2) is sufficient to find the value of x − y. Choice (B) is correct.

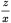Takeaways: Special Cases In Systems Of Linear Equations

• Use Critical Thinking and Pattern Recognition to solve problems involving special cases in systems of linear equations.
• When you are asked to solve for the sum/difference/product/quotient of variables, you may not need to solve for each variable. Don’t assume that you can’t answer a question just because there are more variables present than there are equations.
• Make sure to cancel out or combine variables before you determine that there are more variables than equations.

Practice Set: Special Cases in Systems of Linear Equations on the GMAT

12. What is the value of b?
    1. 5b − a = 3b + 5a
    2. 4(b − a) = 12 − 4a
13. What is the value of a + b?
    1. 5a + 2b = 22
    2. 3b = 30 − 6a
14. If the average (arithmetic mean) of x and y is 30 and 3y + z = 180, what is the value of  ?
    1. 
    2. 
    3. 1
    4. 3
    5. 6