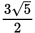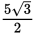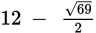Radicals

Learning Objectives

In this section, you will learn how to: 

• Manipulate expressions and perform operations using radical rules
• Apply the Kaplan Methods for Problem Solving and Data Sufficiency to questions with radicals

Fractions as Exponents

A fractional exponent indicates a root. So (read “the nth root of a”). If no specific n is present, the radical sign means a square root. If the numerator in the fractional exponent is a different integer, raise the resulting term to that exponent.

Example: 

Example: 

Rules of Operations with Radical Symbols

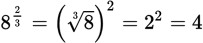
By convention, the symbol  (called radical) means the positive square root only. Even though there are two different numbers whose square is 9 (both 3 and −3), when you see on the GMAT, it refers to the positive number 3 only.

Example:

When it comes to the four basic arithmetic operations, you treat radicals in much the same way you would treat variables.

Addition and Subtraction

Only like radicals can be added to or subtracted from one another.

Example:

Multiplication and Division

To multiply or divide one radical by another, multiply or divide the numbers outside the radical signs, then the numbers inside the radical signs.

Example:

Example: 

Example:

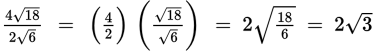
If the number inside the radical is a multiple of a perfect square, the expression can be simplified by factoring out the perfect square.

Example:

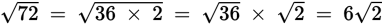
Warning: You cannot “split up” addition underneath a radical sign, although the GMAT will try to trick you into thinking you can.

Example:

Exponents and Powers of 10 with Radicals

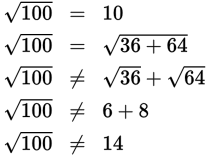
If an exponent is under the square root sign, just divide the exponent by 2. If an exponent is under a cube root sign, divide it by 3.

Example:

If a decimal is under a square root sign, take the square root of the number and divide the number of decimal places by 2. Likewise, if a decimal is under a cube root sign, take the cube root of the number and divide the number of decimal places by 3.

Example:

In-Format Question: Radicals on the GMAT

Now let’s use the Kaplan Method on a Problem Solving question dealing with radicals:

1. 
   1. 
   2. –4
   3. 3
   4. 
   5. 

Step 1: Analyze the Question

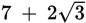
You have to multiply two expressions with square roots in the terms. Note that the numbers under the radical signs are the same; this may be a signal to look at the question more strategically.

Step 2: State the Task

To begin, recall that does not equal . Also, 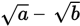does not equal . Thus, in this question, you cannot combine the radicals inside the parentheses; instead, you need to multiply the expressions and 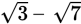using FOIL.

Step 3: Approach Strategically

If you’ve memorized the classic quadratic equations, you might recognize the expression in the stem as the factors of the difference of two squares. Recognizing this pattern will save you time, since you can avoid going through the entire process of applying FOIL.

Remember that (a + b)(a – b) = a² – b².

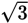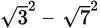Substitute for a, and for b. Then you have , or 3 – 7, which equals −4.

If you hadn’t noticed the shortcut, you could have applied FOIL:

Now, and , so you are left with 3 – 0 – 7 = −4.

Either way, (B) is correct.

Step 4: Confirm Your Answer

Quickly double-check the last calculation step, and you’re done.

Takeaways: Radicals

• Radicals follow the same rules as exponents.
• 
• 
• 
• 
• 
• 
• 
• 

Practice Set: Radicals on the GMAT

7. If a positive number A is equal to  and A, when squared, is equal to the cube root of 27 raised to the fourth power, what is the value of x?
   1. 81
   2. 27
   3. 9
   4. 2
   5. 1
8. If r > 0, is an integer?
   1. r² is an integer.
   2. r = m², where m is an integer.
9. 
   1. 
   2. 
   3. 
   4. 
   5.