.
Factors and multiples are relatively simple concepts used to make some fairly difficult GMAT problems. Multiples—the products of a given integer and other integers—boil down to the numbers you list when counting by a certain number. For example, the multiples of 5 are 5, 10, 15, 20, and so on. Factors—those integers that divide another integer without leaving a remainder—are a little trickier, but this section and the next, on remainders and primes, will show you some ways to determine the factors of a number on Test Day.
A multiple is the product of a given integer and another integer. An integer that is divisible by another integer without a remainder is a multiple of that integer.
Example: 12 is a multiple of 3, since 12 is divisible by 3.
The least common multiple of two or more numbers is the smallest integer that is a multiple of all the numbers or the smallest integer that is divisible by the numbers.
Example: The least common multiple of 6 and 8 is 24, since that is the smallest multiple of 6 that is also divisible by 8 and vice versa.
The factors, or divisors, of a number are the positive integers that divide into that number without a remainder (or a remainder of 0).
Example: The number 36 has nine positive factors: 1, 2, 3, 4, 6, 9, 12, 18, and 36.
You can group these factors in pairs: 1 × 36 = 2 × 18 = 3 × 12 = 4 × 9 = 6 × 6.
These rules can be synthesized into one:
.
The greatest common factor, or greatest common divisor, of a pair of numbers is the largest factor shared by the two numbers.
As with all number properties questions, picking numbers is a useful strategy to use with questions about factors and multiples. When picking numbers, keep in mind the following:
Now let’s use the Kaplan Method on a Problem Solving question dealing with factors and multiples:
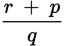
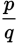
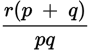
You are given the information that q is a factor of r, so you know that r is a multiple of q. The question stem also says that r is a multiple of p. Thus, r is a multiple of both p and q. This question is very abstract, so picking numbers that are permissible will help you make quick work of the answer choices.
You need to pick numbers for p, q, and r and apply them to the answer choices. Pay Attention to the Right Detail: you are looking for the answer choice that is an integer. Eliminate any answer choices that do not yield an integer.
Based on work in Step 1, you know that r is a multiple of both p and q. So if p = 2 and q = 3, then r = 12 meets the criteria stated in the question stem.
You can now substitute these values into the answer choices. Because this is a “which of the following” question, begin with (E).
Choice (E):
. The answer is an integer, so possibly correct.
Choice (D):
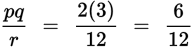. Not an integer. Eliminate.
Choice (C):
. Not an integer. Eliminate.
Choice (B):
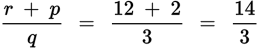. Not an integer. Eliminate.
Choice (A):
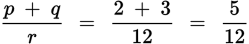. Not an integer. Eliminate.
If all other four answer choices can give non-integers, (E) must be the answer. Note that if you had originally picked different numbers, you may have ended up with more than one answer choice that produced an integer value. Whenever this is the case, you would need to pick a new set of numbers and test only the answer choices that worked out the first time.
(E) also makes logical sense because it equals
, and according to the question stem, q and p are both factors of r , so
and
are both integers. Therefore, their sum must also be an integer.