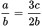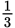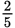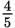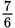, with a colon (x:y), or in English (“the ratio of x to y”). Ratios can (and in most cases, should) be reduced to lowest terms, just as fractions
are reduced.
A ratio is a comparison of two quantities by division. Ratios may be written with
a fraction bar
, with a colon (x:y), or in English (“the ratio of x to y”). Ratios can (and in most cases, should) be reduced to lowest terms, just as fractions
are reduced.
Example: Joe is 16 years old and Mary is 12. The ratio of Joe’s age to Mary’s age is 16 to 12.
In a ratio of two numbers, the numerator is often associated with the word of and the denominator with the word to.
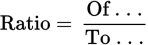
Example: In a box of doughnuts, 12 are sugar and 18 are chocolate. What is the ratio of sugar doughnuts to chocolate doughnuts?
A ratio represents the proportional relationship between quantities or numbers. A ratio can compare either a part to another part or a part to a whole. One type of ratio can readily be converted to the other only if all the parts together equal the whole and there is no overlap among the parts (that is, if the whole is equal to the sum of its parts).
Example: The ratio of domestic sales to foreign sales of a certain product is 3:5. What fraction of the total sales are the domestic sales?
First, note that this is the same as asking for the ratio of the amount of domestic sales to the amount of total sales.
In this case, the whole (total sales) is equal to the sum of the parts (domestic and
foreign sales). You can convert from a part:part ratio to a part:whole ratio.
For every 8 sales of the product, 3 are domestic and 5 are foreign. The ratio of domestic
sales to total sales is then
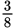or 3:8.
Example: The ratio of domestic to European sales of a certain product is 3:5. What is the ratio of domestic sales to total sales?
Here you cannot convert from a part:part ratio (domestic sales:European sales) to a part:whole ratio (domestic sales:total sales) because you don’t know whether there are any other sales besides domestic and European sales. The question doesn’t say that the product is sold only domestically and in Europe, so you cannot assume there are no other sales. The ratio asked for here cannot be determined.
Some GMAT questions deal with ratios that have three or more terms. Always represent them with colons (e.g., x:y:z).
Even though they convey information about more relationships, ratios involving more than two terms are governed by the same principles as two-term ratios. Ratios involving more than two terms are usually ratios of various parts, and it is usually the case that the sum of these parts equals the whole, making it possible to find part-to-whole ratios as well.
Example: Given that the ratio of men to women to children in a room is 4:3:2, what other ratios can be determined?
The whole here is the number of people in the room, and since every person is either a man, a woman, or a child, you can determine part:whole ratios for each of these parts. Of every nine (4 + 3 + 2 = 9) people in the room, 4 are men, 3 are women, and 2 are children. This gives you three part:whole ratios as follows:
Ratio of men:total people = 4:9 or
.
Ratio of women:total people = 3:9 = 1:3 or
.
Ratio of children:total people = 2:9 or
.
In addition, from any ratio of more than two terms, you can determine various two-term ratios among the parts.
Ratio of women:men = 3:4 or
.
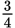Ratio of men:children = 4:2 = 2:1 or
.
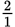Ratio of children:women = 2:3 or
.
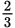And finally, if you were asked to establish a relationship between the number of adults and the number of children in the room, this would also be possible. For every 2 children, there are 4 men and 3 women, which is 4 + 3 = 7 adults. Thus,
Ratio of children:adults = 2:7 or
.
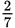Ratio of adults:children = 7:2 or
.
Naturally, a GMAT question will require you to determine only one or at most two of these ratios, but knowing how much information is contained within a given ratio will help you to determine quickly which questions are solvable and which, if any, are not.
Ratios are always reduced to simplest form. If a team’s ratio of wins to losses is 5:3, this does not necessarily mean that the team has won exactly 5 games and lost exactly 3. For instance, if a team has won 30 games and lost 18, its ratio is still 5:3. Unless you know the actual number of games played (or the actual number won or lost), you can’t know the actual values of the parts in the ratio.
Example: In a classroom of 30 first-grade students, the ratio of the 5-year-olds in the class to students in the class is 2:5. How many students are 5 years old?
You are given a part-to-whole ratio (5-year-olds:students). This ratio can also be expressed
as a fraction. Multiplying this fraction by the whole gives the value of the
corresponding part. There are 30 students, and
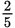of them are 5 years old, so the number of 5-year-olds (5YOs) must be
.
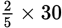For many problems, you can make some deductions about the actual values, even when you aren’t given a total directly. Often, this is the key to solving a challenging proportions question.
Let’s say that a car dealership has used and new cars in stock in a ratio of 2:5. You don’t know the actual number. You know that if there are 2 used cars, there will be 5 new cars. And if there are 4 (or 2 × 2) used cars, there will be 10 (or 5 × 2) new cars. If there are 6 used cars (2 × 3), then there are 15 new cars (5 × 3). In other words, the actual numbers will always equal the figures in the ratio multiplied by the same (unknown) factor.
You can translate from ratios into algebra:
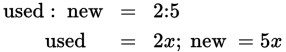
Example: A homecoming party at College Y is initially attended by students and alumni in a ratio of 1 to 5. But after two hours, 36 more students arrive, changing the ratio of students to alumni to 1 to 2. If the number of alumni did not change over those two hours, how many people were at the party when it began?
Besides the 36 additional students who arrive, nowhere are actual numbers referred to directly. But you can jot down the two ratios you’re given in a slightly more useable form:
Translate into algebra. Let x be the number of students initially at the party.
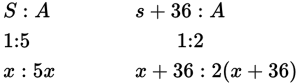
Now you’ve got some equations to work with:
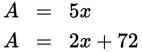
You now have two different expressions for A that are equal. Thus:
Now you know that there were 24 students initially.
Substitute 24 for x to solve for alumni:
The party started with 24 students and 120 alumni, for a total of 144 people.
You may have noticed that many GMAT ratio problems involve things like students, women,
children, cars, and so forth—things that cannot really exist as non-integer values.
(You can’t have
people at a party, for instance!)
There’s a valuable deduction to be made here—if the entities in a problem cannot logically be non-integers, then the factor by which the ratio is multiplied must be an integer. Therefore, the actual number of something must be a multiple of its value in the ratio.
Example:
The question asks for the whole of the ratio for which you are initially given only two parts. The question specifies that there are no other parts to the whole, so you can add the two parts together:
There’s no such thing as “a fraction of a movie,” so the common factor by which you’d multiply 7, 2, and 9 to find the actual numbers must be an integer. That means the number of movies stored on the internet is a multiple of 7, the number of movies stored on the computer is a multiple of 2, and the total—what you’re looking for—must be a multiple of 9.
Take a look at the answers—only (D) is a multiple of 9, so there’s no need to do any more math; (D) must be the answer.
Now let’s use the Kaplan Method on a Problem Solving question dealing with ratios:
For ratio questions, keep careful track of which values are ratios and which are actual quantities. You are told that the ratio of quantities is 2:3. So the smallest value for quantity A is 2 and for quantity B is 3. You could also have any multiple of this ratio, so you could have quantity A = 4 and quantity B = 6, for example.
Now that you have a clear picture of the information, pay Attention to the Right Detail. You are given the ratio of the two quantities, not the exact number of each. Without the actual total value or one of the quantities’ values, you can’t determine the new values. The correct answer is (E).
If you weren’t able to apply this rule so directly, you could solve this question by picking numbers for the possible quantities.
First, test the smallest possible quantities, since these will be the most manageable: quantity A = 2 and quantity B = 3. Adding 6 to each quantity, you get the following new values: quantity A = 8 and quantity B = 9. The new ratio would be 8:9.
Before you select (C), however, you must test a second case. If quantity A = 4 and quantity B = 6, then after adding 6 to each quantity, you get the following new values: quantity A = 10 and quantity B = 12. The new ratio would be 10:12, or 5:6.
You can get two distinct results depending on the original values you choose for the actual quantities, so the correct answer must be (E).
In ratio questions, if you change the actual quantities through multiplication or division, the resulting ratio will be the same, regardless of the starting values of the quantities. However, the same ratio may not be preserved if you add or subtract from the quantities. Knowing this rule is a great way to confirm your answer. Note, by the way, that while this was a Problem Solving question, the GMAT likes to test your understanding of this rule with Data Sufficiency questions in which you need to determine whether you have enough information to solve.
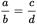, what is the numerical ratio of b to d?
