oz of alcohol in the initial solution. The rest of the solution is water.
Problems involving mixtures may appear intimidating, with their intimations of chemistry, but really they are just proportion, ratio, and percentage problems in disguise. Most mixture questions will ask you to combine two portions that are themselves subdivided into portions. At other times, the question stem may prescribe the ratio of elements in a mixture and then add or remove some or all of one of those portions, asking you to recalculate the new ratio that results. Recognize the familiar patterns at work and you will be a step ahead on the GMAT.
Mixtures on the GMAT are most commonly mixtures of liquids.
Example: You currently have 10 ounces of a solution that is 14 percent alcohol and the rest water. How much water would you have to add to the solution to make the alcohol content equal to 10 percent?
If the solution is 14% alcohol now, that means there are 10 oz ×
oz of alcohol in the initial solution. The rest of the solution is water.
Think critically about this situation, since it’s one that occurs often in mixtures problems: When water is added, the amount of alcohol in the mixture remains constant at 1.4 oz. However, you are told that this same amount of alcohol represents 10% of the resulting mixture.
Since 1.4 is 10% of 14, the final mixture must have a total volume of 14 oz. The difference in volume between the old and new mixtures is accounted for solely by the addition of water, so you’d need to add 14 − 10 = 4 oz of water to make a 10% alcohol solution.
Notice that the only real difference between this and a lot of the proportion or ratio questions that you’ve seen so far in this chapter is that it deals with a liquid, rather than with cars, students, adults, or children. Mixture problems involve many of the same skills you use on other ratio problems, except they require you to keep track of amounts rather than numbers.
Now let’s use the Kaplan Method on a Problem Solving question dealing with mixtures:
%This is a complex question, but there is a straightforward solution. You are creating a new mixture from two others, X and Y. X is 20% bleach, and Y is 45% bleach. The new mixture is to be 35% bleach.
In other words, some amount of a 20% bleach mixture plus some amount of a 45% bleach mixture will balance each other out to form a 35% bleach mixture.
Because this question involves finding a particular balance between Detergents X and Y, you can use the balanced average approach to solve. You could also use algebra or backsolving, but the balanced average approach will be the most efficient. This will let you calculate the proportion of Detergent X in the final mixture.
The question does not state how many parts of Detergent X are used, so call this x. And the question does not state how many parts of Y are used, so call this y. Here’s how it balances:
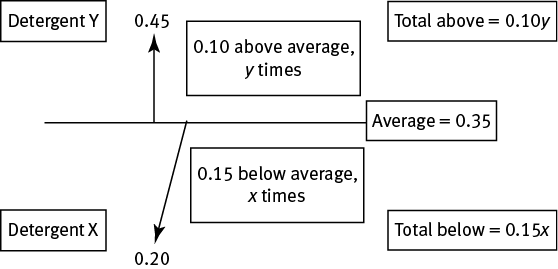
Since the amount above the average has to equal the amount below the average, 0.10y = 0.15x. To solve for a proportional amount, you can view this as a ratio. Divide both sides by y and by 0.15 to get the ratio of x to y:
So x:y is 2:3. Add the total to the ratio to determine how x relates to the total: x:y:total = 2:3:5.
Thus, x:total = 2:5. That means x makes up
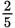, or 40%, of the total mixture. Choice (D) is correct.
Review your calculations for this question. Also, confirm that your answer choice makes sense in the context of the question.
If an amount of a solution containing 10 percent Chemical A is combined with twice as much of a solution that is 30 percent Chemical A and four times as much of a solution that is 35 percent Chemical A, what is the concentration of Chemical A in the resulting solution?