Circles

Circle Concepts and Formulas

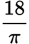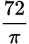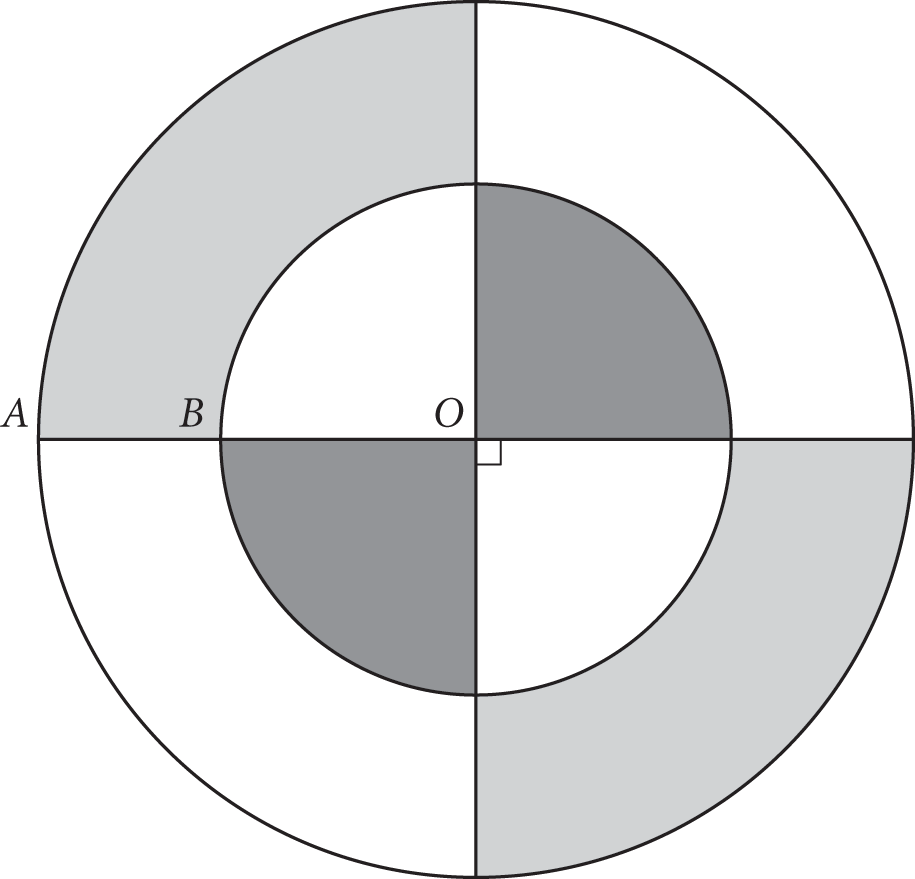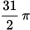
A circle is the set of all points in a plane at the same distance from a certain point. This point is called the center of the circle.

A circle is labeled by its center point: circle O means the circle with center point O. Two circles of different size with the same center are called concentric.

Diameter

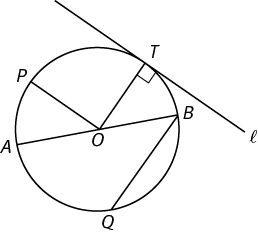
A diameter is a line segment that connects two points on the circle and passes through the center of the circle. In circle O, AB is a diameter.

A circle with center O and diameter AB.  Line segments connect O with points P and T, both located on the circumference of the circle.  An exterior line, labeled L, also intersects the circle at point T, forming a right angle with line segment OT.  Line segment BQ is also drawn, where Q and B are both on the circumference of the circle.

Radius

A radius is a line segment from the center of the circle to any point on the circle. The radius of a circle is one-half the length of the diameter. In circle O, OA, OB, OP, and OT are radii.

Chord

A chord is a line segment joining two points on the circle. In circle O, QB and AB are chords. A diameter of a circle is a longest chord of the circle.

Central Angle

A central angle is an angle formed by two radii. In circle O, ∠AOP, ∠POB, ∠AOB, along with others, are central angles.

Tangent

A line that touches only one point on the circumference of the circle is tangent to that circle. A line drawn tangent to a circle is perpendicular to the radius at the point of tangency. Line ℓ is tangent to circle O at point T.

Circumference and Arc Length

The distance around a circle is called the circumference. The number π (“pi”) is the ratio of a circle’s circumference to its diameter. The value of π is 3.14159265 . . . , usually approximated as 3.14. For the GMAT, it is usually sufficient to remember that π is a little more than 3.

Since π equals the ratio of the circumference to the diameter, a formula for the circumference is:

C = πd

or

C = 2πr

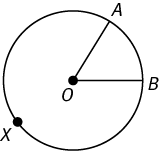
An arc is a portion of the circumference of a circle. In the figure below, AB is an arc of the circle that spans central angle AOB. The shorter distance between A and B along the circle is called the minor arc; the longer distance AXB is the major arc. An arc that is exactly half the circumference of the circle is called a semicircle (in other words, half a circle).

A circle with center O contains points A, B, and X on its circumference.  Radii AO and BO form interior angle AOB.

The length of an arc is the same fraction of a circle’s circumference as its degree measure is of the degree measure of the circle (360°). For an arc with a central angle measuring n degrees:

Arc length = 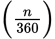× circumference

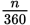= × 2πr

Example:

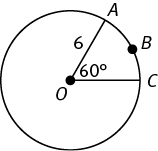
Circle with center O and arc ABC.  Angle AOC measures 60 degrees and radius AO has a length measuring 6.

What is the length of arc ABC of the circle with center O above?

Since circumference = 2πr and the radius is 6, the circumference is 2 × π × 6 = 12π.

Since ∠AOC measures 60°, the arc is 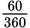, or one-sixth, of the circumference.

Therefore, the length of the arc is 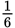× 12π, or 2π.

Inscribed Angle and Arc Length

An inscribed angle is one that opens up from the edge of a circle instead of its center. Here, angle ABC is inscribed.

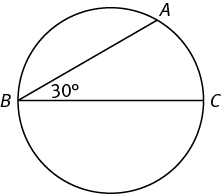
A circle contains points A, B, and C on its circumference.  Inscribed angle ABC has a measure of 30 degrees.

An inscribed angle also has a relationship with minor arc length. For an inscribed angle measuring n degrees:

Arc length = 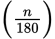× circumference

In other words, an angle that’s inscribed defines an arc twice as long as one defined by a central angle of equal angle measure.

Area of a Circle

The area of a circle is given by this formula:

Area = πr2

A sector is a portion of the circle bounded by two radii and an arc. In the circle below with center O, OAB is a sector. To determine the area of a sector of a circle, use a similar method to the one you used to find the length of an arc: determine what fraction of 360° is in the degree measure of the central angle of the sector, then multiply that fraction by the area of the circle.

Circle with center O contains points A and B on its circumference, forming sector AOB.  Angle AOB has a measure of n degrees.

Area of sector = × (Area of circle)

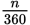= × πr2

Example:

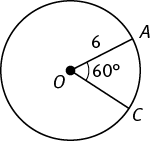
A circle with center O, radius 6, and angle AOC measuring 60 degrees.

What is the area of sector AOC in the circle with center O above?

Since ∠AOC measures 60°, a 60° “slice” is 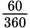, or one-sixth, of the circle. So the sector has an area of 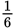× πr2 = 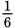× π(6)2 = × 36π = 6π.

In-Format Question: Circles on the GMAT

Now let’s use the Kaplan Method on a Problem Solving question dealing with circles:

  1. If the diameter of a circle increases by 50 percent, by what percent will the area of the circle increase?
    1. 25%
    2. 50%
    3. 100%
    4. 125%
    5. 225%
Step 1: Analyze the Question

For any geometry question without a figure, it is important to draw a quick sketch of the described figure to avoid simple mistakes on Test Day. So on your notepad, you should draw two circles: (1) the original circle and (2) the circle with increased diameter.

Two circles side by side. One has a diameter about twice the length of the other's.

Now look at the question stem again. Notice that this is a percent question in disguise and that you are not given the original or final diameter. This is a great candidate for picking numbers.

Step 2: State the Task

You want the percent increase of area from the small circle to the large one. If you use picking numbers, the task will be much more straightforward, as you will be solving for the increase between two numbers rather than two algebraic expressions.

Step 3: Approach Strategically

To make your calculations manageable, consider that the area of a circle is given in terms of its radius and the radius is of the diameter. So you want the diameter to be a multiple of 2. Suppose that the original diameter is 4. Then the original radius is (4) = 2. Therefore, the area of the original circle is

πr2 = π(2)2 = 4π

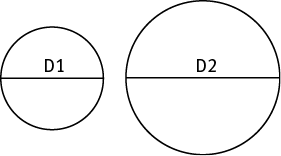
The diameter of 4 is increased by 50%, or . The new diameter is 4 + (4) = 4 + 2 = 6. Therefore, the new radius is (6) = 3. The area of the new circle is:

πr2 = π(3)2= 9π

To calculate the percent increase between the two circles, use the following equation:

The correct answer is (D).

Step 4: Confirm Your Answer

Be very careful how you apply the percent increase equation. A common error is to use the wrong value in the denominator. Another is to solve not for the percent difference but for how much one amount is as a percent of another. (E), for example, is the answer to “The area of the circle after the increase is what percent of its original area?” Always take a moment to confirm that your answer choice makes sense logically.

Practice Set: Circles on the GMAT

  1. The length of an arc on circle C formed by a central angle measuring 60° is 12. What is the diameter of the circle?
    3. 6π
    5. 12π
  2. One circle inside another circle. They share a center O. Four radii divide the smaller circle and larger circle into four sectors. One sector has a central angle of 90 degrees.
    The figure above represents a circular garden, with center O. AB is 4 feet, and BO is 3 feet. The gardener plans to plant sunflowers in the two light gray sections and tulips in the two dark gray sections. How much more area, in square feet, will be covered by sunflowers than tulips?

    2. 8π
    4. 20π
    5. 31π
  3. If two circles overlap each other, what is the area of that overlap?
    1. The edge of each circle intersects the center of the other circle.
    2. The sum of the circumferences of the two circles is 12π.