A solid is a three-dimensional figure (a figure having length, width, and height) and is, therefore, rather difficult to represent accurately on a two-dimensional page. Figures are drawn in perspective, giving them the appearance of depth. If a diagram represents a three-dimensional figure, that fact will be specified in the accompanying text.
Fortunately, only a few types of solids appear with any frequency on the GMAT: rectangular solids (including cubes) and cylinders. These are both uniform solids (solids in which the measure of each dimension is constant through the entire object). Other types, such as spheres, may appear, but these questions typically will involve only understanding the solid’s properties and not applying any special formula.
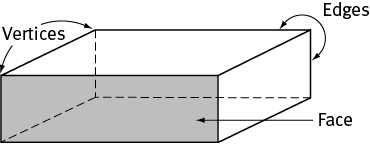
Here are the terms used to describe the common solids:
The vertices of a solid are the points at its corners. For example, a cube has eight vertices.
The edges of a solid are the line segments that connect the vertices and form the sides of each face of the solid. A cube has 12 edges.
The faces of a solid are the polygons that are the boundaries of the solid. A cube has six faces, all squares.
The volume of a solid is the amount of space enclosed by that solid. The volume of any uniform solid is equal to the area of its base times its height.
In general, the surface area of a solid is equal to the sum of the areas of the solid’s faces.

A rectangular solid is a solid with six rectangular faces (all edges meet at right angles). Examples are cereal boxes, bricks, etc.

Volume = Area of base × Height = Length × Width × Height
V = l × w × h
Surface area = Sum of areas of faces
SA = 2lw + 2lh + 2wh
It’s common for difficult geometry questions to ask you to calculate the length of a rectangular solid’s diagonal (one that runs from lower-front-left to upper-back-right, for example).
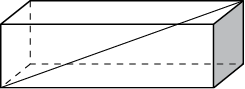
There’s a simple formula to calculate the diagonal. It looks a lot like the Pythagorean theorem (in fact, it’s derived using that theorem).
Diagonal2 = Length2 + Width2 + Height2
A cube is a special rectangular solid with all edges equal (l = w = h), such as a die or a sugar cube. All faces of a cube are squares.

Volume = Area of base × Height = Edge3
V = l × w × h = e3
Surface area = Sum of areas of faces = 6 × Edge2
SA = 6e2
A cylinder is a uniform solid whose horizontal cross section is a circle. An example is a soup can. You need two pieces of information to find the volume and surface area of a cylinder: the radius of the base and the height.
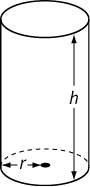
Volume = Area of base × Height
V = πr2 × h
Lateral surface area (LSA) = Circumference of base × Height
LSA = 2πr × h
Total surface area = Areas of bases + LSA
SA = 2πr2 + 2πrh
You can think of the surface area of a cylinder as having two parts: one part is the top and bottom (the circles), and the other part is the lateral surface. In a can, for example, the area of either the top or the bottom is just the area of the circle, or lid, which represents the top; hence, πr2 for the top and πr2 for the bottom, yielding a total of 2πr2. For the lateral surface area, the area around the can, think of removing the can’s label. When unrolled, it’s actually in the shape of a rectangle. One side is the height of the can, and the other side is the distance around the circle, or circumference. Hence, its area is h × (2πr), or 2πrh. Thus, the total surface area is 2πr2 + 2πrh.
A sphere is made up of all the points in space a certain distance from a center point; it’s like a three-dimensional circle. The distance from the center to a point on the sphere is the radius of the sphere. A basketball is a good example of a sphere. A sphere is not a uniform solid; the cross sections are all circles, but they are of different sizes. (In other words, a slice of a basketball from the middle is bigger than a slice from the top.)
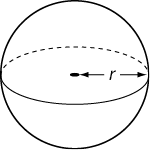
It is not important to know how to find the volume or surface area of a sphere, but occasionally a question might require you to understand what a sphere is.
Now let’s use the Kaplan Method on a Data Sufficiency question dealing with solids:
This Value question requires you to determine whether there is sufficient information to find how long it takes to fill a rectangular tank with a uniform depth with water. Not only do you need the volume of the tank, but you also need the rate at which the tank is being filled.
Statement (1) tells you that the tank is 4 feet wide and 10 feet long. Because you are not given any information about the depth, you cannot determine the volume of the tank. Furthermore, you are not given any information about the rate at which the tank is filled with water. This statement is insufficient. You can eliminate (A) and (D).
Statement (2) tells you that the tank is being filled at a rate of 1.5 cubic feet per minute. You have no information with which to determine the volume of the tank, so you cannot determine how long it will take to fill the tank with water. Eliminate (B).
Now you must combine statements. You know the length of the tank, the width of the tank, and the rate at which it is being filled. Because you do not know the depth of the tank, you cannot determine its volume. Because you cannot determine the volume of the tank, you cannot solve for how long it takes to fill the tank with water. The two statements taken together are insufficient, and (E) is correct.
 , what is the volume of the empty space inside the cube?
, what is the volume of the empty space inside the cube?