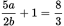4 ← numerator (also known as the dividend)
— ← fraction bar (means divided by)
5 ← denominator (also known as the divisor)
When you multiply the numerator and denominator by the same number (any number other than zero), the fraction is unchanged. You simply get an equivalent fraction.
Example:
Similarly, dividing the top and bottom by the same nonzero number leaves the fraction unchanged.
Example:
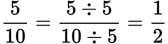
The GMAT often uses this technique to change the form of fractions that have radicals in the denominator.
Example:
Generally speaking, when you work with fractions on the GMAT, you’ll need to put them in the lowest terms. That means that the numerator and the denominator are not divisible by any common integer greater than 1.
Example: The fraction
is in lowest terms, but the fraction
is not, since 3 and 6 are both divisible by 3.
The method you use to take a fraction and put it in lowest terms is called reducing. That simply means to factor and divide out any common multiples from both the numerator and denominator. This process is also commonly called canceling. Canceling is particularly useful to avoid time-consuming calculation.
Example: Reduce
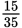to lowest terms.
First, determine the largest common factor of the numerator and denominator. Then, divide the top and bottom by that number to reduce.
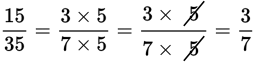
We can’t add or subtract two fractions directly unless they have the same, or a common, denominator.
A common denominator is just a common multiple of the denominators of the fractions. The least common denominator (LCD) is the least common multiple (LCM): the smallest positive number that is a multiple of all the terms.
Example:
Denominators are 5, 3, 2.
Least common denominator (LCD) = 30.
For each fraction, divide the LCD by the denominator.
|
Then, multiply the numerator and denominator by that result. Combine the numerators by adding or subtracting and keep the LCD as the denominator. |
|
To multiply fractions, simply multiply the numerators together and the denominators together. Often, this process can be sped up by canceling common factors before you multiply.
Example:
First, reduce (cancel) diagonally and vertically.
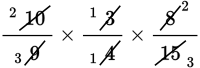
In this case, divide both 10 in the numerator and 15 in the denominator by their common factor 5. Likewise, 3 in the numerator and 9 in the denominator can be reduced by factoring out a 3. Finally, 8 in the numerator and 4 in the denominator can be divided by the common factor 4.
Then multiply the numerators together and the denominators together.
To divide one fraction by another, you actually multiply the first fraction by the reciprocal of the divisor (the second fraction).
To get the reciprocal of a fraction, invert it. Simply switch around the numerator
and the denominator. For example, the reciprocal of the fraction
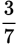is
.
Example:
Invert the divisor, then multiply as usual.
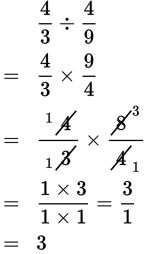
A complex fraction is a fraction that contains one or more fractions in its numerator or denominator. There are two methods for simplifying complex fractions.
Method I: Use the distributive law. Find the least common multiple of all the denominators and multiply all the terms in the top and bottom of the complex fraction by the LCM. This will eliminate all the denominators, greatly simplifying the calculation.
Example:
|
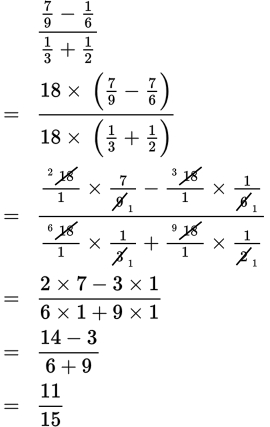
The LCM of all the denominators is 18. |
Method II: Treat the numerator and denominator separately. Combine the terms in each to get a single fraction on top and a single fraction on bottom. You are left with the division of two fractions, which you perform by multiplying the top fraction by the reciprocal of the bottom one. This method is preferable when it is difficult to get an LCM for all of the denominators.
Example:
|
The LCM of the numerator is 22. The LCM of the denominator is 16. |
If the numerators are the same, the fraction with the smaller denominator will have the larger value, since the numerator is divided into a smaller number of parts.
Example:
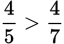
If the denominators are the same, the fraction with the larger numerator will have the larger value.
Example:
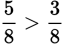
If neither the numerators nor the denominators are the same, express all of the fractions in terms of some common denominator. The fraction with the largest numerator will be the largest.
One version of this method is to multiply the numerator of the left fraction by the denominator of the right fraction and vice versa (similar to cross multiplying). Then compare the products obtained this way. If the left product is greater, then the left fraction was greater to start with.
Example: Compare
and
.
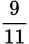Compare 5 × 11 and 9 × 7.
Because 55 < 63,
.
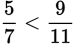Example: Compare
and
.
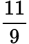As before, the comparison can be made by cross multiplying.
Compare 22 × 9 and 11 × 19.
Because 198 < 209,
.
You can also convert the fractions to percents or decimals for easy comparison. This technique is especially useful when finding a common denominator seems time-consuming.
Example: Compare
,
,
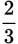and
.
,
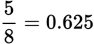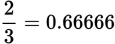. . . , and
. . .
Because 0.625 < 0.636363 . . . < 0.66666 . . . ,
.
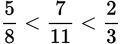Converting fractions to decimals or percents frequently comes up on the GMAT. Often, the problem gives you fractions in the question but percents in the answer choices. It’s a good idea to memorize the common fraction-to-decimal equivalencies for Test Day.
Another way to compare fractions is to find a “benchmark value” against which the fractions can be compared, particularly when dealing with large numbers.
Example: Compare
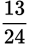and
.
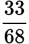Both are very close to
.
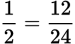and
.
Because
and
,
.
Fractions whose numerators are greater than their denominators may be converted into
mixed numbers and vice versa. Mixed numbers consist of an integer and a fraction.
For example,
,
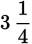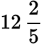, and
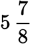are all mixed numbers.
Example: Convert
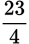to a mixed number.
Example: Convert
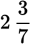to a fraction.
Decimals can be converted to common fractions with a power of 10 in the denominator.
Example:
Numbers are made up of digits in specific places. The GMAT occasionally asks questions using the terms digit and place, so you should be familiar with the naming convention:
When a GMAT question specifies that a variable is a digit, the only possible values are the integers between 0 and 9, inclusive.
To compare decimals, add zeros after the last digit to the right of the decimal point until all the decimals have the same number of digits. Doing this will make all the denominators of the fractions the same. Therefore, comparing the numerators will determine the order of values.
Example: Arrange in order from smallest to largest: 0.7, 0.77, 0.07, 0.707, and 0.077.
Because 70 < 77 < 700 < 707 < 770, 0.07 < 0.077 < 0.7 < 0.707 < 0.77.
When adding or subtracting decimals, make sure that the decimal points are lined up, one under the other. This will ensure that the corresponding places are added: that is, tenths are added to tenths, hundredths to hundredths, etc.
Example:
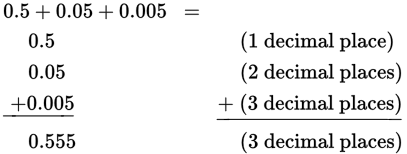
To multiply two decimals, initially multiply them as you would integers and ignore the decimal places. The number of decimal places in the product will be the sum of the number of decimal places in the factors that are multiplied together.
Example:
Division—Method I: When dividing a decimal by another decimal, multiply each by a power of 10 such that the divisor becomes an integer; that is, move the decimal point of each the same number of places. (This doesn’t change the value of the quotient.) Then carry out the division as you would with integers, placing the decimal point in the quotient directly above the decimal point in the dividend.
|
Example: |
0.675 ÷ 0.25 = |
Move the decimal point over two places to the right to make 0.25 an integer. |
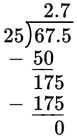
Division—Method II: Turn the division problem into a fraction. It is best when the numbers have common factors. Move the decimal point in the numerator and the denominator an equivalent number of places to make both numbers integers. Then cancel common factors.
Example: 0.675 ÷ 0.25
Now let’s use the Kaplan Method on a Problem Solving question dealing with fractions:
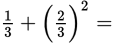
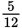
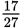
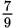
You’re given an expression with two fractions, one of which is raised to an exponent. Attention to the Right Detail is important here; in this case, note the use of the parentheses around only one of the fractions.
Follow the order of operations (PEMDAS); start with the parentheses, then add the fractions by finding a common denominator.
First, square both the numerator and denominator of
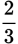, giving a value of
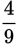. Then find a common denominator for the two fractions
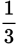and
. Multiply the numerator and denominator of
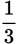by 3, which yields
. Now that the denominators are the same, you can add the two fractions
, which gives you the answer,
, choice (C).
Take a moment to verify your math, particularly making sure you followed the order of operations and accurately converted fractions into forms that have a common denominator. Note that (D) would be a tempting wrong answer if you had first added the two fractions and then squared the result.
?
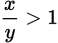
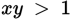
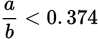
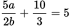is equivalent to each of the following EXCEPT:
