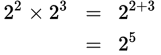
In the term 3x2, 3 is the coefficient, x is the base, and 2 is the exponent. The exponent refers to the number of times the base is multiplied by itself. For instance, in 43, you multiply 4 by itself 3 times: 43 = 4 × 4 × 4 = 64.
Accurately distinguishing among these elements is important. For instance, in the expression 3x2, only the x is being squared (x is the base), not the 3 (3 is the coefficient). In other words, 3x2 = 3(x2). If you wanted to square the 3 as well, you would need to rewrite the term as (3x)2 to make 3 part of the base. Remember that in the order of operations, you raise to a power before you multiply, so in 3x2, you square x and then multiply by 3.
A number multiplied by itself is called the square of that number (e.g., 5 × 5 or 52 is 5 squared).
A number multiplied by itself two times is called the cube of that number (e.g., 4 × 4 × 4 is 43 or 4 cubed).
To multiply two terms with the same base, keep the base and add the exponents.
Example:
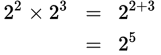
To divide two terms with the same base, keep the base and subtract the exponent of the denominator from the exponent of the numerator.
Example:
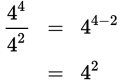
To raise a power to another power, multiply the exponents.
Example:
To multiply two terms with the same exponent but different bases, multiply the bases together and keep the exponent.
Example:
Any number raised to the first power equals itself: a1 = a.
Any number except zero that is raised to the zero power is equal to 1: a0 = 1. The exception to this rule is when the base is also equal to zero (00 is undefined).
A negative exponent indicates a reciprocal. To arrive at an equivalent expression, take the reciprocal of the base and change the sign of the exponent.
Example: 
When raising a fraction to an exponent, you can solve in one of two ways: either by raising the numerator and the denominator to the exponent separately, or by multiplying the whole fraction by itself the number of times indicated by the exponent. Either approach yields the same result.
|
Example: |
|
Note that the squared value here,
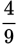, is less than the base,
. Raising a positive fraction less than 1 to a positive exponent greater than 1 results
in a smaller value. The higher the exponent, the smaller the result.
The exponent of a base of 10 tells you how many zeros the number would contain if written out.
Example: 106 = 1,000,000 (6 zeros), since 10 multiplied by itself 6 times is equal to 1,000,000.
When multiplying a number by a power of 10, move the decimal point to the right the same number of places as in the exponent; that is, the number of zeros in that power of 10.
When dividing by a power of 10, move the decimal point the corresponding number of places to the left. (Note that dividing by 104 is the same as multiplying by 10−4.)
Now let’s use the Kaplan Method on a Data Sufficiency question dealing with exponents:
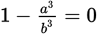
This is a Yes/No question. You need to determine whether there is enough information to answer the question “Does a = b?” There is no information provided in the question stem, so look at the statements.
Statement (1) says that a2 − b2 = 0, which is the same as saying a2 = b2. Now if a2 = b2, then either a = b or a = −b. You can test a few cases by picking numbers. If a = 5 and b = 5, then a2 = b2, so Statement (1) is true and a = b. The answer to the question is yes.
If a = 5 and b = −5, then a2 = b2 because 52 = (−5)2 = 25, so Statement (1) is true and a is not equal to b. The answer to the question is no. Because more than one answer to the question is possible, Statement (1) is insufficient. You can eliminate (A) and (D).
Statement (2) tells you that
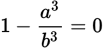, which can be simplified as
or a3 = b3. In the equation a3 = b3, both a and b are raised to the same odd exponent. Remembering the rules governing exponents, you
know that when raised to an odd power, positive numbers yield positive results and
negative numbers yield negative results. So if a3 = b3, you can now conclude that a = b. The answer to the question is always yes, and Statement (2) is sufficient. The
correct answer is (B).
If you weren’t sure about the rules of exponents, you could use picking numbers to evaluate Statement (2). In order for a3 to equal b3, a and b must have the same value. For instance, if a = −5 and b = −5, then a3 = b3 because (−5)3 = (−5)3 = −125. You cannot pick numbers such as a = 5 and b = −5, since 53 = 125 ≠ (−5)3 = −125. Since it’s impossible to pick different numbers for a and b, the answer to the question is always yes, and you can choose (B).
Note how the Core Competency of Attention to the Right Detail plays a big role in answering the question correctly. It’s easy to be misled into thinking that if a2 = b2, then a must be equal to b. Pay attention to whether exponents are even or odd when confronted with a similar problem.
, what is the value of x?