Median, Mode, Range, and Standard Deviation

Learning Objectives

In this section, you will learn how to: 

• Identify the median, mode, and range of a set of values and use these measures to solve for unknown values
• Define standard deviation and explain how this statistic is calculated
• Apply the Kaplan Methods for Problem Solving and Data Sufficiency to questions addressing median, mode, range, or standard deviation

Median

If an odd group of numbers is arranged in numerical order, the median is the middle value.

Example: What is the median of 4, 5, 100, 1, and 6?

First, arrange the numbers in numerical order: 1, 4, 5, 6, and 100. The middle number (the median) is 5.

If a set has an even number of terms, then the median is the average (arithmetic mean) of the two middle terms after the terms are arranged in numerical order.

Example: What is the median value of 2, 9, 8, 17, 11, and 37?

Arrange the values in numerical order: 2, 8, 9, 11, 17, 37. The two middle numbers are 9 and 11. The median is the average of 9 and 11, that is, 10.

The median can be quite different from the average. For instance, in the first set of numbers above, {1, 4, 5, 6, 100}, the median is 5, but the average is .

Mode

The mode is the number that appears most frequently in a set. For example, in the set {1, 2, 2, 2, 3, 4, 4, 5, 6}, the mode is 2.

It is possible for a set to have more than one mode. For example, in the set {35, 42, 35, 57, 57, 19}, the two modes are 35 and 57.

Range

The range is the positive difference between the largest term in the set and the smallest term. For example, in the set {2, 4, 10, 20, 26}, the range is 24.

Standard Deviation

Standard deviation measures the dispersion of a set of numbers around the mean. If you’ve worked with the standard deviation formula in high school or college, you might remember that the formula looks like this:

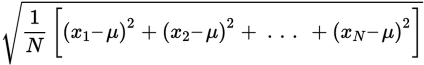
It can be intimidating, so let’s paraphrase it in plain English. Calculating the standard deviation involves the following steps:

1. Find the average (arithmetic mean) of the set.
2. Subtract the average of the set from each term in that set.
3. Square each result.
4. Take the average of those squares.
5. Calculate the positive square root of that average.

Fortunately, the GMAT will only very rarely require you to apply this formula, and only on the most difficult questions. When standard deviation is tested, all you will generally need to understand is the basic concept: standard deviation represents how close or far the terms in a list are from the average.

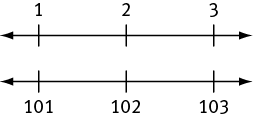
Thus, {1, 2, 3} and {101, 102, 103} have the same standard deviation, since they both have one term on the average and two terms exactly one unit away from the average. A quickly sketched number line can confirm this:

The set {1, 3, 5} will have a smaller standard deviation than {0, 3, 6}. Both sets have an average of 3, but the first has terms 2, 0, and 2 units from the average while the second has terms 3, 0, and 3 units from the average. Again, you can confirm this with a quick sketch:

You could also calculate the standard deviation for the sets {1, 3, 5} and {0, 3, 6} to confirm:

Since 6 is larger than , you can see that the standard deviation of the second, more widely spaced set of numbers is larger than that of the first set. However, you will save much time on Test Day by using your understanding of how standard deviation works to estimate rather than calculating the answers to questions such as these.

In other words, the GMAT test makers are more interested in whether you understand the concept of standard deviation and can apply Critical Thinking to situations that involve it than in whether you can perform complex mathematical calculations.

In-Format Question: Median, Mode, Range, and Standard Deviation on the GMAT

Now let’s use the Kaplan Method on a Data Sufficiency question dealing with median, mode, range, and standard deviation:

1. List L consists of 12, 8, 10, 14, and 6. If two numbers are removed from list L, what is the standard deviation of the new list?
   1. The range of the new list is 8.
   2. The median of the new list is 8.

Step 1: Analyze the Question Stem

This is a Value question. You know that two numbers are removed from the list 12, 8, 10, 14, 6. You want to determine the standard deviation of the new list. There is no other information given, so let’s look at the statements.

Step 2: Evaluate the Statements Using 12TEN

Statement (1): You are told that the range of the new list is 8. The only way to have a range of 8 is for both 6 and 14 to appear in the new list, because any other pair of numbers in the original list will be closer to one another than 8. So the new list must contain 6 and 14.

The new list will also contain one of the numbers 8, 10, and 12. If, for example, the third number in the list is 10, then the list will be 6, 10, and 14. If the third number in the list is 12, then the numbers in the list will be 6, 12, and 14. The standard deviation of the list 6, 10, and 14 will be different from the standard deviation of the list 6, 12, and 14 because the two sets have different means and the numbers in the two lists are dispersed differently around the mean.

More than one standard deviation is possible, and therefore more than one answer to the question is possible. Statement (1) is insufficient. Eliminate choices (A) and (D).

Statement (2) says that the median of the new set is 8. Because there will be an odd number (3) of members of the new list, 8 will have to appear in the list in order for 8 to be the median. Additionally, since 8 must be in the middle of the new list and there is only one possible value less than 8, you know that 6 must also be in the list. The new list could be 6, 8, 10, which has a median of 8, and the new list could also be 6, 8, 14, which also has a median of 8.

The standard deviation of the numbers in the list 6, 8, 10 is less than the standard deviation of the list 6, 8, 14. More than one standard deviation is possible, and therefore more than one answer to the question is possible. So Statement (2) is insufficient. You can eliminate choice (B).

Now that you’ve determined that Statement (1) and Statement (2) are both insufficient on their own, look at the statements together: you know from Statement (1) that 6 and 14 must be in the list, and you know from Statement (2) that 6 and 8 must be in the list. The statements taken together tell you that the list must consist of 6, 8, and 14. Because there is only one possible list, there can only be one standard deviation. The statements taken together are sufficient. (C) is correct.

Takeaways: Median, Mode, Range, And Standard Deviation

• In a list with an odd number of terms arranged in ascending or descending order, the median is the middle term.
• In a list with an even number of terms arranged in ascending or descending order, the median is the average of the two middle terms.
• The mode of a list of terms is the term(s) that appear(s) most frequently.
• The range is the positive difference between the largest term in the list and the smallest term.
• Standard deviation measures the dispersion of a set of numbers around the mean. The GMAT will hardly ever require you to apply the formula for standard deviation. Instead, use Critical Thinking and quick sketches of number lines to determine how close the terms in a list are from the average.

Practice Set: Median, Mode, Range, and Standard Deviation on the GMAT

1. Data set S contains the elements {−5, x, 2, 0, −1, 1, 9}. What is the value of x?
   
   
   1. The average (arithmetic mean) of data set S is 2.
   2. The median of data set S is 1.

2. If the range of the eight numbers 17, 8, 14, 28, 9, 4, 11, and n is 25, what is the difference between the greatest possible value of n and the least possible value of n?

   1. 1
   2. 3
   3. 21
   4. 26
   5. 29
3. In the list of numbers {a, b, c}, a is the average (arithmetic mean) of the list and b + c = 0. What is the standard deviation of a, b, and c?
   1. b − a = 2
   2. c − a = 2
4. Given the set of even numbers {2, 18, 32, x, y}, what is the median of the set?
   1. y(y − 1) = 30
   2.