Sequences of Integers

Learning Objectives

In this section, you will learn how to: 

• Recall that in a list of consecutive values, the average (arithmetic mean) equals the median
• Find the number of terms in a list of consecutive integers
• Calculate the sum of a sequence of consecutive integers
• Apply the Kaplan Methods for Problem Solving and Data Sufficiency to questions dealing with sequences of integers

Average and Median of Consecutive Integers

The average, or mean, of a set of consecutive integers will equal its median.

Example: What is the average of 1, 2, 3, 4, and 5?

For this set, 3 is both the mean and the median. This is always the case for sets of consecutive or evenly spaced integers.

There is another way to calculate the average of this set. The average of a series of consecutive or evenly spaced integers is also the same as the average of its first and last terms. For the last example, that works out to .

Sum of Numbers

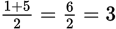If you know the average of a group of numbers and how many numbers are in the group, you can find the sum of the numbers. You can think of it as if all the numbers in the group are equal to the average value.

Sum of values = Average value × Number of values

Example: What is the sum of all the integers between 1 and 66 inclusive?

Since this is a series of consecutive integers, you can find its average by averaging the first and last terms: .

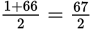To find the number of terms in a set of consecutive integers, take the difference between the largest and the smallest numbers and add 1.

Sum of values = Average value × Number of values

Granted, you still have to calculate 67 × 33, but that is much easier than adding all 66 numbers!

You may also have to find a sum in what might seem to be a normal average problem.

Example: The average daily temperature for the first week in January was 31 degrees Fahrenheit. If the average temperature for the first six days was 30 degrees, what was the temperature on the seventh day?

The sum for all 7 days = 31 × 7 = 217 degrees.

The sum for the first 6 days = 30 × 6 = 180 degrees.

The temperature on the seventh day = 217 − 180 = 37 degrees.

In-Format Question: Sequences of Integers on the GMAT

Now let’s use the Kaplan Method on a Problem Solving question dealing with sequences of integers:

1. In a new housing development, trees are to be planted in a straight line along a 166-foot stretch of sidewalk. Each tree will be planted in a square plot with sides measuring 1 foot. If there must be 14 feet between each plot, what is the maximum number of trees that can be planted?
   1. 8
   2. 9
   3. 10
   4. 11
   5. 12

Step 1: Analyze the Question

Though this is not a geometry question, a quick sketch of the situation will help illustrate how to solve it.

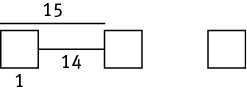
So you know that the unit of one tree and one space is 1 foot + 14 feet = 15 feet.

Step 2: State the Task

To find how many trees can be planted, determine the feet required for a tree and the space between trees. Then divide the total length of the sidewalk by the unit of 1 tree and the space between trees.

Step 3: Approach Strategically

Each tree takes up 1 foot, and each space takes up 14 feet. Together, they take up 15 feet. Now find how many times 15 goes into the total number of feet on one side of the sidewalk:

166 ÷ 15 = 11, with a remainder of 1 foot

You can plant 1 last tree in the remaining foot, bringing the total number of trees to 12. This means along the sidewalk, you can plant 12 trees with 11 spaces between them, as long as you start and end with a tree. (E) is correct.

Step 4: Confirm Your Answer

Make sure your answer makes sense in the context of the question. Did you take into account the remainder of the division? Will an entire tree fit in the remaining space? You can use these questions to confirm your work.

Takeaways: Sequences Of Integers

• In a sequence of consecutive or evenly spaced integers, the average, or mean, equals the median.
• To find the number of terms in a sequence of consecutive integers, take the difference between the largest and the smallest and add 1.
• To find the sum of a sequence of consecutive or evenly spaced integers, multiply the average of the largest and the smallest term by the number of terms.
• To find the sum of any set of numbers, multiply the average by the number of terms.

Practice Set: Sequences of Integers on the GMAT

5. The sum of a sequence of consecutive integers is 1,125 and the median is 45. What is the value of the greatest integer in the sequence?
   1. 33
   2. 45
   3. 56
   4. 57
   5. 58
6. What is the sum of the multiples of 4 between 13 and 125 inclusive?
   1. 1,890
   2. 1,960
   3. 2,200
   4. 3,780
   5. 4,400
7. If z is the sum of three consecutive odd positive integers, is z evenly divisible by 9?
   1. When the smallest of the three numbers is divided by 3, the remainder is 1.
   2. The smallest of the three numbers is divisible by 7.
8. The sum of a sequence of six consecutive positive integers is Z. The sum of terms in a different sequence of five consecutive integers is Z − 5. If the greatest term of the five-number sequence is 40, what is the difference between the median term of the five-number sequence and the least term of the six-number sequence? 
   1. 5
   2. 7
   3. 8
   4. 9
   5. 10