
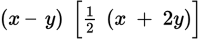

Often, the most frustrating aspect of word problems is the odd way in which information is presented. Don’t get frustrated. Just break down the information into small pieces and take things one step at a time. Word problems can usually be translated from left to right, but not always. Say you see this sentence: “There are twice as many dollars in George’s wallet as the amount that is 5 dollars less than the amount in Bill’s wallet.” Instead of trying to translate it into math all in one go, approach it piecemeal.
Whenever possible, choose letters for your variables that make sense in the context of the problem. You could start by calling the amount in George’s wallet G and the amount in Bill’s wallet B. Now, think about the relationship between the two amounts: G is not compared to B but to 5 dollars less than B, or (B − 5). You can now say that G is twice as large as (B − 5). So if you were to set them equal to each other, you’d have to multiply (B − 5) by 2. The equation is G = 2(B − 5).
If you had tried to translate it in the order it’s written, you might have come up with something like 2G = 5 − B, and you can be sure that there’d be a wrong answer choice waiting to take advantage of that. So think carefully before you translate.
The hardest part of word problems is the process of taking the English sentences and extracting the math from them. The actual math in word problems tends to be the easiest part. The following translation table should help you start dealing with English-to-math translation.
|
Word Problems Translation Table |
|
|
English |
Math |
|
equals, is, was, will be, has, costs, adds up to, the same as, as much as |
= |
|
times, of, multiplied by, product of, twice, double, by |
× |
|
divided by, per, out of, each, ratio |
÷ |
|
plus, added to, and, sum, combined |
+ |
|
minus, subtracted from, smaller than, less than, fewer, decreased by, difference between |
− |
|
a number, how much, how many, what |
x, n, etc. |
Take a look at the following example:
|
Beatrice’s wage |
is |
3 dollars more than |
twice Alan’s wage |
|
↓ |
↓ |
↓ |
↓ |
|
B |
= |
3 + |
2A |
Start by breaking the problem down into smaller, more manageable pieces:
Always take the time to make sure you are translating the problem correctly. Improper translation will cost you points.
Answers follow this exercise.
Translate the following sentences into algebra. When names are used, use the first letter of each person’s name as the appropriate variable.


Now let’s use the Kaplan Method on a Problem Solving question dealing with translating words into expressions and equations:
This problem may look complicated at first, but it’s really just asking you to translate the English sentence into math. Once the word problem has been translated, you can apply basic algebra to simplify the statement to match the correct answer choice.
You need to translate the word problem into math.
Look at the word problem and work from left to right to extract your algebraic statements. Rather than picking x and y for your variables, use C for Charles’s age and S for Sarah’s age:
Six years from now, Charles’s age will be C + 6.
Two years ago, Sarah’s age was S − 2.
Now connect these two algebraic statements. You are told that in 6 years, Charles will be at least as old as Sarah was 2 years ago. The phrase “will be at least as old as” implies that Charles could be exactly the same age as Sarah 2 years ago, or he could be older. Therefore, use the “greater than or equal to” sign between the two statements:
C + 6 ≥ S − 2
The correct answer is (E).
This translation directly matches (E), but be careful to check that the variables are in the correct order and that you have used the correct inequality sign.