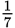than you would with the unwieldy decimal 0.1428571 . . .
Proportionality shows up on the GMAT in the form of fractions, ratios, decimals, and percents. Fundamentally, proportions represent relationships. You deal with proportionality every day, even if you might not realize it. Rates and speeds, for example, are expressed as ratios: a car travels 30 miles per hour, or a worker earns $80 per task. You can use these proportional relationships to determine how many miles a car travels at this speed over a given length of time or how many tasks a worker must complete in order to earn a given amount of money. Prices are also ratios: a certain item costs $4.50, so the ratio of items to dollars is 1:4.5. Then you could use a proportion to discover how much 24 of the same item would cost. Note that knowing the proportional relationship of one thing to another does not tell you how many things you have. For example, if the ratio of gerbils to parrots in a pet store is 2:3, you don't know the exact number of gerbils or parrots. However, you do know that for every 2 gerbils the store has, there are 3 parrots as well.
Often the GMAT tests proportions in the form of word problems, so the translation skills you learned in the Algebra chapter (a form of Paraphrasing) will continue to be valuable here as you cut through the seeming novelty of the given “story” to understand the underlying proportional relationships being described.
Here are the answers to the questions you were asked to consider.
One of the most important skills you can develop for dealing with proportions questions
on the GMAT is the ability to convert quickly among percent, decimal, fractional,
and ratio forms of the same value. This skill is so crucial because GMAT problems
often mix these various formats within the same problem—getting all the values expressed
in the same way will make them easier to handle. Also, certain values are just easier
to work with in one format or another. For instance, you’d much rather perform arithmetic
operations with the fraction
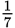than you would with the unwieldy decimal 0.1428571 . . .
In this problem, you may choose to express 45 percent as a decimal (0.45); as a fraction
(
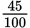, which reduces to
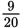); or as a ratio (45:100, which reduces to 9:20), depending on which is easiest
to work with at the time. Remembering that percent simply means “out of 100” is the key to making these conversions. Later in this chapter, you will find a chart to help you memorize some of the common conversions you’re most
likely to need on Test Day.
A lot of information is given in this question, so it is especially important that you organize your scratchwork effectively. You are asked for the number of games a team still needs to win in order to achieve a certain winning percentage. You are given the team’s winning percentage so far, the number of games it’s played so far, and the number of games it still needs to play, so you have all the information you need to solve arithmetically.
As is usual on the GMAT, this question doesn’t necessarily give you the information in the most convenient form, so you will have to do some calculating to figure out the actual number of games the team has won so far and the total number of games the team will have played, but these calculations are possible, so you can solve this question arithmetically. (We will return to this question and solve it using the Kaplan Method later this chapter.)
If that approach was the one that first occurred to you, that’s fine—and you’re not alone. You have likely been rewarded all your academic life for knowing how to do the “schoolroom math,” and this approach can get you the correct answer on the GMAT as well. What might not have occurred to you initially is the other strategy you could use to solve this problem: backsolving. Whenever you are asked to solve for a single value (here, it’s the number of games the team still needs to win) and the answer choices are all simple numerical values, it may be quicker and easier to answer the question by plugging the values in the answer choices into the scenario described in the question stem.
More guidance on backsolving is available in the Problem Solving chapter of this book; it’s a highly efficient strategy, and it’s well worth becoming comfortable with, even if you are generally expert at solving using “classroom math.”
There are various unknowns in this question that the unwary test taker might mistakenly choose as the correct answer—but to the wrong question. As you practice, never choose an answer choice simply because you recognize that number from your calculations; some of these choices are likely to be traps.
This question asks you for the number of additional games the team must win. Possible trap answers are the number of wins so far—choice (A)—and the total number of wins the team needs—choice (E).
The final step of the Kaplan Method for Problem Solving is to confirm your answer; by double-checking that you are answering the question that was asked, you will avoid this all-too-common mistake.
As you’ve seen throughout the Quant section, Critical Thinking is necessary for deciding on the most efficient strategic approach, and Attention to the Right Detail will ensure that you answer the question that is asked instead of falling for trap answers. Specifically on proportions questions, you will use your skill in Paraphrasing to convert ratios into the form that’s easiest for that problem. You will also pay Attention to the Right Detail so that you don’t confuse different types of ratios such as part-to-part and part-to-whole.
Now let’s apply the Kaplan Method for Problem Solving to the proportions question you saw earlier:
You are given the percentage of games a team has won for the first 80 games and the number of games it has yet to play (82). You are asked to calculate how many more games the team needs to win to have a 50% win record.
You need to calculate the total number of games that will be played, then the total number of those that need to be won for a 50% record. Then calculate how many games have already been won and subtract that from the total number of wins needed.
First, add the 80 games that have already been played to the number of remaining games to get the total games: 80 + 82 = 162. To win 50% of the games, the team would need to win half of these, or 81. You can use the percentage given to calculate how many games the team has already won: 45% of 80.
The number of the games the team still needs to win is 81 – 36 = 45. Choice (B) is correct. 45% can be expressed as
. Use this fraction when multiplying:
.
The answer choices are small, manageable numbers, so you may want to use backsolving,
especially if you’re not sure how to set up the arithmetic. If you choose to backsolve,
remember to think about exactly what the answer choices represent: the number of additional
games the team needs to win. Start with choice (B), 45 games. Calculate the games already won, 
, and add the 45 additional games: 36 + 45 = 81.
Now you can ask yourself, is 81 half (or 50%) of all the games? The team’s already played 80, and there are 82 left to play, so 80 + 82 = 162 and, yes, choice (B) is 50% of 162.
If you had instead backsolved starting with (D), you would have ended up with too high a proportion of games won (91 of 162) and known that you needed a smaller number of wins during the second part of the season in order to end up with a winning percentage of 50%.
Review your calculations to be sure they’re correct. You can also verify that your answer is logical using Critical Thinking: the team would need more than 40 additional wins to make up for the fact that it won less than 50% of its first 80 games.
Now let’s look at each of the areas of proportions that show up on the GMAT Quantitative section, starting with how ratios relate to proportions.