, or 0.333 . . .) and 1:2 (or
, or 0.5). (A) and (B) are both in that range, but all the others are above 1:2. So you can make a guess—with
50% odds of being right—just by analyzing the problem logically.
A well-placed guess can sometimes be the best thing you can do on a problem. Because of the severe penalty exacted on those who fail to finish a section, you need to stay on a steady pace. If you fall behind, it’s a good idea to guess on the hardest problems. That way you’ll get back lost time instead of falling further behind. And while you shouldn’t be afraid to guess, you should be afraid to rush! The GMAT builds in twists and writes problems in complicated ways; rushing almost always leads to a misperception of the problem. The test makers base many wrong answers on the most common misperceptions. So rushing through a problem virtually guarantees a wrong answer. It’s far better to guess as needed than to rush through an entire section.
Sometimes you just have no idea how to approach a problem. Instead of throwing away 3 or 4 minutes getting frustrated, make a guess. If you didn’t know how to approach the problem, you weren’t likely to choose the right answer in any case, and you can use the time you save to solve other problems that you stand a better chance of answering correctly.
Lastly, there are some problems that are best solved using guessing techniques. The two keys to good guessing are (1) elimination of likely wrong answers by using your knowledge of the problem and of the GMAT’s tendencies and (2) maintaining your focus on the “big picture”—remembering that your performance on the section as a whole matters much more than your performance on two or three questions. Better to make a guess in 1 minute and be done with a hard problem than spend 6 minutes before guessing; the extra time will pay off.
Also, keep in mind that the hardest questions are the ones you’ll be most likely to need to guess on—and are also the ones that will hurt your score the least when you get them wrong. So don’t be afraid to guess!
There are five guessing strategies that you can apply to Problem Solving:
You won’t be able to use all of these strategies on every problem. But if you run through the checklist and eliminate whatever choices you can, you’ll make your best possible guess in the least possible amount of time. Let’s look at the strategies.
Some answers are simply logically impossible. By analyzing and simplifying before attempting to solve, you may learn enough about the problem to eliminate many wrong answer choices. Consider this problem:
It seems a challenging problem at first glance. But the simplified version of the
problem is that you’re adding a 1:2 solution to a 1:3 solution. So logically, the
right answer has to be between 1:3 (or
, or 0.333 . . .) and 1:2 (or
, or 0.5). (A) and (B) are both in that range, but all the others are above 1:2. So you can make a guess—with
50% odds of being right—just by analyzing the problem logically.
In case you were curious, the answer is (B). The 12-ounce solution has 4 ounces of alcohol and 8 ounces of water. The 8-ounce solution has 2 ounces of alcohol and 6 ounces of water. Add the amounts of alcohol and water to get 6 ounces of alcohol and 14 ounces of water for a ratio of 3:7 alcohol to water.
Also, note that Roman numeral questions are good candidates for logic-based guessing. If you can evaluate only one statement, you can still logically eliminate several answers.
The GMAT asks some questions that are intended to be solved via estimation. When a question stem includes a word like approximately, that’s a clear signal that estimation is the best approach you can take.
Example:
If you had a calculator on the Quant section, you could quickly figure out that the product in question is 3,715,891,200. But with no calculator, what can you do? The keys to the solution are the word “closest” and the big spread of values in the answer choices—each is 10 times the nearest value. This problem has “estimation” written all over it.
Jot down the numbers in question:
2 × 4 × 6 × 8 × 10 × 12 × 14 × 16 × 18 × 20
Now, how to estimate these values? Since each answer is a power of 10, you should estimate each value in a way that easily relates to 10:
2 × 4 × 6 × 8 × 10 × 12 × 14 × 16 × 18 × 20
2 × 4 × 6 × 10 × 10 × 10 × 10 × 20 × 20 × 20
What about the small ones? 2 × 4 × 6 = 48, which is very close to 50.
50 × 10 × 10 × 10 × 10 × 20 × 20 × 20
Continuing to look for tens:
(5 × 10) × 10 × 10 × 10 × 10 × (2 × 10) × (2 × 10) × (2 × 10)
That’s eight 10s, one 5, and three 2s:
2 × 2 × 2 × 5 × 108
(2 × 2) × (2 × 5) × 108
4 × 10 × 108
4 × 109
That’s closer to 109 than to 1010, so (D) is the correct answer. No calculator needed, just the willingness to estimate!
The test makers lay psychological traps as well as mathematical ones, and this guessing principle helps you to stay out of them. It’s part of human psychology to deal with being lost by looking for familiar things. When you get lost in a problem, you tend to grab hold of familiar numbers, such as those you’ve just seen in the question stem. The GMAT doesn’t like to reward people who get lost with right answers, so such numbers tend to be wrong.
This is psychology again. Our eyes are attracted to difference. (Next time you watch a movie or a TV show, notice how often no one else is dressed in the same color as the main character—it’s a subtle trick to keep your attention where the director wants it.) Random guessers, then, will be attracted to uniqueness. As the GMAT does not like to reward random guessing, the oddballs should be eliminated.
A word of warning about this technique: the GMAT also uses a little reverse psychology. The test makers know that people tend to be afraid of answers that seem too out of line with the others. These outlying values, then, will sometimes be correct. What Kaplan means by an “oddball,” then, is not a number that’s notably bigger or smaller but an answer choice that is structurally unique—the only fraction or the only negative number, for example.
Look at these five answer choices, for example:
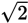
In this case, the answer choice 2,056 is not an oddball and should not be eliminated. But 
is and should be.
Because the GMAT is a test of critical thinking, answers that you’d get just by mashing numbers together are usually wrong. Consider this question:
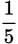
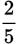
It’s true that you want
2 of the
5 marbles in the bag. But GMAT questions usually
require a little more math than just that, so
isn’t likely to be correct. (In fact, it’s the odds of getting
1 red marble when selecting
1; the probability of getting
2 red when selecting
2 is actually
.)
Believe it or not, there are some GMAT problems for which a guessing strategy—most notably Logic or Estimation—is the best approach you could take. Remember that the test makers aren’t trying to judge your math skills alone; they are also testing your ability to find efficient solutions to problems. Every so often, they give you a set of choices with only one logically possible answer. Make sure to look at the answer choices before you choose your approach. Otherwise, you might not realize that you can estimate.
Example:
It’s true that you could pick the original price to be $100, but you can do better here by thinking logically about the question and the answer choices. The price goes up 20% and then up another 15%. That 15% increase is being applied not to the original price but to the price after the first increase. If it were 15% of the original, then the total increase would be 20% + 15% = 35% (that’s the “uncritical solution”). But since the second increase is based on a higher starting price, the total increase will be a little more than 35%. Only one answer, choice (C), fits the bill, so it must be correct.
If applied strategically, guessing will be a great tool for you on Test Day. It will help keep you out of time management trouble, help you to feel confident and in charge of the test, and occasionally reward you with a very quick right answer.