Answers and Explanations

Practice Set: Translating Words into Expressions and Equations on the GMAT

  1. (E)
    Step 1: Analyze the Question

    The sentences in this word problem can be translated into algebraic statements to determine the total number of paper clips produced by both machines over a given number of hours. Alternatively, numbers could be picked for r and t and arithmetic could be done, but algebra is the more efficient approach if you are comfortable with it. 

    Step 2: State the Task

    Find the expression that represents the number of paper clips both machines working together produce in t hours.

    Step 3: Approach Strategically

    Translate the phrase “s is 30 greater than r” as s = r + 30. Thus, the two machines produce r + r + 30 = 2r + 30 paper clips in each hour. In t hours, that would be t(2r + 30). That’s (E).

    Step 4: Confirm Your Answer

    If you solve using algebra, you could pick numbers to confirm: say r = 10, then s = 10 + 30 = 40. Together, the machines produce 10 + 40 = 50 paper clips each hour. If t = 2, then the machines produce 50 × 2 = 100 paper clips in 2 hours. When you plug the numbers you picked into the answer choices, only (E) equals 100. 

  2. (A)
    Step 1: Analyze the Question

    You can apply the translation rules to this word problem to convert the question into a manageable algebraic equation.

    Step 2: State the Task

    Once the word problem has been translated, apply basic algebra to simplify the statement to match the correct answer choice.

    Step 3: Approach Strategically

    Let x be the age of the youngest sibling in years. Then the ages of the other siblings, who are 3, 5, and 8 years older than the youngest sibling, are x + 3, x + 5, and x + 8, respectively. The average age of the four siblings is 21. Therefore, the average of x, x + 3, x + 5, and x + 8 is 21.

    The average formula is 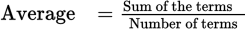. So you can write the equation .

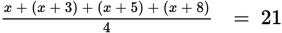    Solve the equation for x:

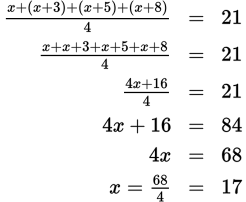
    The correct answer is (A).

    Step 4: Confirm Your Answer

    For Average questions, an easy way to confirm your answer is to plug your value for x into the average formula and see if the same answer comes out on both sides. If not, go back over your calculations.

Practice Set: Isolating a Variable on the GMAT

  1. (E)
    Step 1: Analyze the Question

    You are provided with an equation with fractions in terms of the variables a, b, c, d, and e. The answer choices are also fractions with variables.

    Step 2: State the Task

    Use algebra to manipulate the equation so that  is on one side and all other terms are on the other side.

    Step 3: Approach Strategically

    To isolate the variable e, cross multiply the given equation to eliminate the fractions: 2(3a − 2ce) = 3(4b − 2de). Distributing 2 on the left side of the equation and 3 on the right side gives 6a − 4ce = 12b − 6de.

    Add 6de to both sides so that all terms that contain e are on one side of the equation: 6a − 4ce + 6de = 12b.

    Subtract 6a from both sides so that only terms with e are on the left: −4ce + 6de = − 6a + 12b.

    Factoring out e yields e(−4c + 6d) =  − 6a + 12b.

    Dividing both sides by (−4c + 6d) results in . Simplify the fraction on the right by dividing each term by 2: .

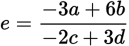    Your task is not to solve for e but for 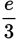. Thus, . None of the choices match, but (E) is close. Multiplying this expression by  does not change its value but does change the sign of each term, resulting in . Thus, (E) is correct.

    Step 4: Confirm Your Answer

    Double-check that you solved for the right expression; (C) represents the value of e rather than .

  2. (D)
    Step 1: Analyze the Question

    The question provides a complicated-looking equation in terms of two variables. Since the answer choices are all numbers, however, there must be a way to find a numerical value for the requested expression.

    Step 2: State the Task

    Find the value of s − r.

    Step 3: Approach Strategically

    The fact that x − y = −(y − x) is an important idea for the GMAT. For example, you may use this property to reexpress algebraic expressions to match the given answer choices. Here, a variation can be used to simplify the equation in the question stem, , to solve for s − r. Begin by dividing both sides by 2:

    To multiply the numerator by −1, simply reverse the terms: 

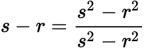
    Cancel common factors:

    (D) is correct.

    Step 4: Confirm Your Answer

    If you have time, double-check your algebra.

  3. (B)
    Step 1: Analyze the Question

    You’re given a relationship between the desktop computer’s electricity usage and the laptop computer’s electricity usage in terms of a variable, and you’re also given the combined electricity usage in terms of another variable. Either straight algebra or picking numbers could work here.

    Call the desktop computer’s usage D and the laptop’s usage L.

    Because the laptop uses s fewer watts than the desktop, the L = D − s.

    Because the sum of the desktop’s usage and the laptop's usage is t watts, you have the equation D + L = t. You also know that L = D − s, so you can use substitution to rewrite this equation as D + (D − s) = t.

    Step 2: State the Task

    Isolate the desktop computer’s electricity usage in terms of the given variables.

    Step 3: Approach Strategically

    Now that you’ve translated the facts of the problem into math expressions, you can solve the equation for D:

    Thus, (B) is correct.

    Alternatively, you could pick numbers. Say the combined electricity usage, t, is 100 watts and the desktop uses 70 watts. This means the laptop uses 30 watts, or 40 fewer watts than the laptop; therefore, s = 40. Plug these values of t = 100 and s = 40 into the answer choices to see which choice matches the desktop’s wattage of 70:

    (A): 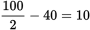. Eliminate.

    (B): 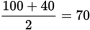. Keep for now and check the remaining answers.

    (C): 100(40 − 1) = 3,900. Eliminate.

    (D):  . Eliminate.

    (E): 100 − (2 × 40) = 20. Eliminate. So (B) is correct.

    Step 4: Confirm Your Answer

    If you solved algebraically, be sure you correctly translated the words into mathematical expressions. If you picked numbers, check that each variable is assigned the correct value.

Practice Set: Quadratic Equations on the GMAT

  1. (A)

    Step 1: Analyze the Question Stem

    In this Yes/No question, sufficiency means determining that x is either definitely positive or definitely not positive (zero or negative).

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) provides a quadratic equation in which the sign of the constant term (16) is positive. A plus sign here means the quadratic has roots (value(s) of x) that are either both positive or both negative. Thus, this statement is sufficient to answer the question with either a clear yes or no. Don’t take the time to find the value of x, but if you did, you would reverse-FOIL to find that x2 − 8x + 16 = (x − 4)(x − 4) = 0, meaning that x − 4 = 0 and x = 4; the answer to the question is yes. Eliminate (B), (C), and (E). 

    Statement (2) provides a quadratic equation in which the sign of the constant term (−12) is negative. You don’t need to factor the equation to determine whether this is sufficient, because a negative sign in this position of a quadratic guarantees that it has two roots—one positive and one negative. This statement is therefore insufficient. Eliminate (D) and choose (A).

  2. (D)
    Step 1: Analyze the Question

    The question stem provides the equation n2 − 4n = 12, which can be restated as the quadratic equation n2 − 4n − 12 = 0.

    Step 2: State the Task

    The question asks which of the answer choices could be equal to zero, given the values of n that are consistent with the equation in the stem.

    Step 3: Approach Strategically

    When a quadratic equation is set equal to 0 and factored, one of the factors must be equal to 0 and the possible values of the variable are derived from that fact. Therefore, if an expression in the choices shares a common factor with the given equation, that expression could be equal to 0.

    The equation in the question stem factors to (n − 6)(n + 2) = 0. So factor the choices to determine whether they have either n − 6 or n + 2 as a factor. If they do, they could be equal to zero.

    (A) is n2 − 2n − 15 = (n + 3)(n − 5). Eliminate.

    (B) is n2 − 2n + 1 = (n − 1)(n − 1). Eliminate.

    (C) is n2 + 4n − 12 = (n − 2)(n + 6). Be careful here! The factors of this expression reverse the signs of the factors of the given equation. Eliminate.

    (D) is n2 − 5n − 6 = (n − 6)(n + 1). The factor (n − 6) is shared by the given equation, so (D) is correct.

    For the record, (E) is n2 + 6n + 5 = (n + 5)(n + 1). Eliminate.

    (D) shares a factor with the given equation, so it is correct.

    Step 4: Confirm Your Answer

    When factoring quadratics, an easy way to check your work is to expand the binomials back into their original form by applying the FOIL technique. If time permits, do this for every quadratic expression you factor to avoid calculation errors.

  3. (D)
    Step 1: Analyze the Question

    This is a Roman numeral question involving equations with x raised to various exponents; expect that you’ll have to do some factoring. 

    Step 2: State the Task

    Determine which of the equations could be equal to 0.

    Step 3: Approach Strategically

    No statement is markedly easier to work with than the others, and Statement I shows up the most in the choices, so start there. Factor the expression into 3(x2 − 4) = 3(x + 2)(x − 2). If x is 2 or −2, the expression is 0. Statement I must be part of the correct answer, so eliminate (B).

    Evaluate Statement II next. Notice that both variable terms, x2 and x4, will never be negative, since any real base raised to an even exponent is either zero or positive. Therefore, this expression cannot be less than the constant term, 1. Eliminate (C) and (E).

    Evaluate Statement III by factoring x2 + 7x + 6 into (x + 6)(x + 1). The expression will be 0 if x = −6 or x = −1. (D) is correct.

    Step 4: Confirm Your Answer

    In Roman numeral questions, make sure you pick the choice that includes all the valid statements and none of the invalid statements.

Practice Set: Systems of Linear Equations on the GMAT 

  1. (B)
    Step 1: Analyze the Question

    The question provides information about the 42 countries a photographer has been to, which are on 3 continents. The number of visited countries on each continent can be represented by a variable, and there’s enough information to set up three equations. Thus, you’re able to solve for any of the three variables.

    Step 2: State the Task

    Use a system of linear equations to determine the number of countries in Asia that the photographer has visited.

    Step 3: Approach Strategically

    Let S represent the number of countries in Asia, F the number in Africa, and E the number in Europe. Since there are 42 countries total, F + E + S = 42. Also, since the photographer has been to 6 more countries in Europe than in Asia, E = S + 6. Twice as many in Africa as in Europe gives F = 2E.

    It follows that, since E = S + 6, F = 2E = 2(S + 6). So by substitution: 

    Therefore, the photographer has been to 6 countries in Asia, and the answer is (B).

    Step 4: Confirm Your Answer

    As always, be sure to answer the right question. (C) is the number of countries visited in Europe, and (E) is the number visited in Africa. If time permits, plug 6 back into the word problem as the number of countries in Asia and see whether you come up with 42 total countries: Asia = 6; Europe = 6 + 6 = 12; Africa = 2 × 12 = 24. Finally, 6 + 12 + 24 = 42. 

  2. (C)

    Step 1: Analyze the Question Stem

    This is a Value question. The question stem says that Paula’s used book collection is worth $104 and asks how many are histories, but there is no information about any other books or their worth.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) tells you that Paula has only mysteries at $1 apiece and histories at $25 apiece. If m is the number of mysteries and h is the number of histories, the total worth can be stated as the number of each type of book times the unit worth: 104 = 1m + 25h. Since you have one equation with two variables, this is insufficient. Eliminate (A) and (D).

    Statement (2) states that there are exactly 4 mysteries with a total worth of $4. Thus, the worth of each mystery is $1, and the total worth of the histories is $104 − $4 = $100. Lacking information about the worth per history book, this statement is also insufficient. Eliminate (B) and evaluate the statements together. 

    Statement (1) says that history books are worth $25 each, and from Statement (2), you know that the history books are worth $100 each. This is sufficient to determine the number of history books, so (C) is correct.

  3. (E)
    Step 1: Analyze the Question

    The question provides information about two people’s ages at varying points in time. The answer choices are integers, but because they represent a sum of two unknown ages, backsolving would not be an efficient strategy here. 

    Step 2: State the Task

    Determine the sum of the two people’s ages 3 years from now, or (L + 3) + (M + 3) = L + M + 6. You’ll need to translate the words into algebraic equations and then solve the system of equations for the unknown.

    Step 3: Approach Strategically

    That Leonard’s age in 8 years will be twice Mikala’s current age can be written as L + 8 = 2M. Note that you age Leonard by 8 years by adding 8 to L, but you don’t add any years to M because this statement deals with Mikala’s current age. Because the task is to find the sum of their ages, rearrange this so the L and M terms are on the same side of the equal sign: L − 2M = −8.

    Leonard’s age 2 years ago is L − 2, so twice that age is 2(L − 2). And 2 years ago, Mikala’s age was M − 2, so five times that age is 5(M − 2). The equation for the second sentence is thus 2(L − 2) + 5(M − 2) = 51. Distribute the 2 and 5 across the parentheses: 2L − 4 + 5M − 10 = 51. Simplify: 2L + 5M = 65.

    There is no way to directly add or subtract these equations to find L + M, but if you add the equations, the two terms have the same coefficient, which can then be divided out. Thus, combination is an efficient approach.

    The question asks for the sum of the two ages in 3 years: L + M + 6 = 19 + 6 = 25. (E) is correct.

    Step 4: Confirm Your Answer

    Be certain that you correctly untangled the question stem and that you answered the question that was asked. (C) is the sum of the ages now. (D) is the sum of the ages plus 3 years, but both Leonard and Mikala will be 3 years older, so 3 needs to be added twice. 

Practice Set: Special Cases in Systems of Linear Equations on the GMAT

  1. (B)

    Step 1: Analyze the Question Stem

    This Value question stem gives no information about b. Thus, move on to the statements. For sufficiency, a statement must supply information that would allow you to calculate a single value for b.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) is 5b − a = 3b + 5a. Simplifying this equation yields 2b = 6a, which is b = 3a, but neither variable cancels out. Thus, you have one equation with two variables, and you can’t solve for the value of either variable. Therefore, there is not enough information to find the value of b. Statement (1) is insufficient. Eliminate (A) and (D).

    Statement (2) is 4(b − a) = 12 − 4a. Simplify this equation to see whether a variable cancels out. Multiplying out the left side of the equation gives 4b − 4a = 12 − 4a. Adding 4a to both sides yields 4b = 12, so the variable a cancels out in the simplification, leaving you with one linear equation containing only one variable, b, which you could solve for. Thus, Statement (2) is sufficient, and (B) is correct. 

    If you see a question like this one on Test Day, don’t be too quick to assume that you need two equations to solve for the value of either variable—be sure to simplify the equation first.

  2. (C)

    Step 1: Analyze the Question Stem

    In this Value question, you must determine whether there is sufficient information to determine the value of a + b. Note that this may not require finding the individual values of a and b; solving for the value of the entire expression would suffice. Because no information is given in the question stem, move on to the statements.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) provides one equation with two variables, 5a + 2b = 22. Because the number of variables is greater than the number of different equations, there’s no way to solve for the values of a and b. Moreover, there’s no way to isolate a + b on one side. Thus, Statement (1) is insufficient. Eliminate (A) and (D).

    Statement (2) gives 3b = 30 − 6a, which is one equation with the two variables a and b. Rearranging this gives 6a + 3b = 30; dividing each term by 3 yields 2a + b = 10. Again, because the number of variables is greater than the number of different equations, and because there’s no way to simplify for the value of a + b, Statement (2) is insufficient. Eliminate (B).

    Now look at the statements together. You have two distinct linear equations and two variables, so you can solve for their values. Therefore, the two statements taken together are sufficient, and (C) is correct. For the record, here’s the math: if you rearrange the equation in Statement (2) by adding 6a to both sides, you get 6a + 3b = 30. Now use combination, subtracting one equation from the other, to solve for a + b in one step:

  3. (D)
    Step 1: Analyze the Question

    You’re given the average of x and y and the value of 3y + z. There are two equations and three variables, so look for a way to eliminate y, which is not part of the value you’re solving for.

    Step 2: State the Task

    Find the value of  .

    Step 3: Approach Strategically

    Translate “the average of x and y is 30” as . Multiply both sides by 2 to find that x + y = 60. Since you need the value of , isolate each of these variables: x + y = 60, so x = 60 − y, and 3y + z = 180, so z = 180 − 3y. Therefore, 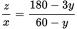 . Factoring out a 3 from the numerator yields 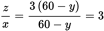. The correct choice is (D).

    Here’s another approach. After getting x + y = 60, multiply this equation by 3 to get 3x + 3y = 180. Since 3y + z = 180, you can set the two equations equal to each other: 3x + 3y = 3y + z. Subtract 3y from both sides to find 3x = z. Now divide both sides by x: .

    Step 4: Confirm Your Answer

    Confirm that you’ve found   and not  , which is (B). You can also pick numbers to confirm: since the average of x and y is 30, choose x = 30 and y = 30. Then 3y = 90, so since z = 180 − 3y, z = 90. Then  .

Practice Set: Sequences on the GMAT

  1. (D)
    Step 1: Analyze the Question

    You are provided with the definition of an arithmetic sequence and told that l, m, n, o, p is one such sequence. As this is a Roman numeral question with variables, expect to use picking numbers and don’t forget to check the Roman numeral statements in the most efficient order. In this question, you will want to begin with Statement III, as it shows up the most in the answer choices.

    Step 2: State the Task

    Determine which of the Roman numeral statements are true.

    Step 3: Approach Strategically

    Statement III: To test this statement, say the original arithmetic sequence is 6, 9, 12, 1 5, 18 (adding a constant of 3 each time). Statement III would have you subtract 5 from each term, which results in the sequence 1, 4, 7, 10, 13. This is still an arithmetic sequence as each term is exactly 3 more than its preceding term, so Statement III is a true statement. Eliminate (A) and (B).

    Of the remaining statements, Statement I is easier to test. Using the same original sequence you had above, Statement I would have you multiply each term by 3. Doing so results in the sequence 18, 27, 36, 45, 54. This is still an arithmetic sequence as each term is exactly 9 more than its preceding term, so Statement I is a true statement. Eliminate (C) and (E).

    Therefore, the correct answer is (D).

    Step 4: Confirm Your Answer

    To confirm the answer, test Statement II: Using the same original sequence picked above, Statement II would have you square each term. The larger numbers can make this time-consuming, but just squaring the first three terms (36, 81, 144) should be enough to show you that Statement II does not result in an arithmetic sequence. (D) is confirmed.

  2. (B)
    Step 1: Analyze the Question

    The question stem provides the formula for a sequence and the values for the fifth and sixth terms in the sequence, t5 and t6.

    Step 2: State the Task

    Determine the value of the second term in the sequence, t2.

    Step 3: Approach Strategically

    Work backward from the known values until you get to t2. For t6, the tn−2 term is t4 and the tn−1 term is t5. Plug the two known values into the formula for the series to get 152 = 3(t4) + 2(51) − 1. This simplifies to 3(t4) = 51, so t4 = 17. For t5, the formula is 51 = 3(t3) + 2(17) − 1. Thus, 3(t3) = 18 and t3 = 6. One more to go! For t4, 17 = 3(t2) + 2(6) − 1. So 3(t2) = 6 and  t2 = 2, which is (B).                                      

    Step 4: Confirm Your Answer

    (D) is t3 and (E) is t4. Checking your scratchwork to make sure you’ve calculated through to the correct number in the sequence will help you avoid these wrong answer traps.

  3. (D)

    Step 1: Analyze the Question Stem

    This is a Value question. You must determine what information is needed to solve directly for the term S2. The question stem says that if Sn is the nth term of the sequence, then for n > 2, you have Sn = Sn−1 + Sn−2. That is, after the second term in the sequence, the next term is equal to the sum of the two previous terms. For example, the third term is equal to the sum of the first and second terms.

    You also know that S1 is 4. Because S3 = S2 + S1, S3 = S2 + 4. So you have one linear equation with two variables, S3 and S2. To find the value of S2, you need more information that will lead to a single possible value for S2.

    You could find the value of S2 if you were given the value of S3. You could also find the value of S2 if you were given another linear equation with the variables S3 and S2 that is different from the first equation. Look at the statements.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) says that S3 = 7. Because S3 = S2 + 4, you have the equation 7 = S2 + 4. From this equation, you can find the single possible value of S2. Statement (1) is sufficient. Eliminate (B), (C), and (E).

    Statement (2) says that S4 = 10. Because S4 = S3 + S2, you have the equation S3 + S2 = 10. This is another linear equation containing the terms S2 and S3. Because the two equations are distinct, you have enough information to determine the values for both S3 and S2. Statement (2) is sufficient. (D) is correct.

Practice Set: Functions and Symbolism on the GMAT

  1. (D)
    Step 1: Analyze the Question

    This is a symbolism problem containing two definitions and a nested function. You will need to begin with the innermost function and work your way outward.

    Step 2: State the Task

    Find the value of image.

    Step 3: Approach Strategically

    Symbolism problems may look frighteningly complicated, so it’s important to remember that they are nothing more than dressed-up equations for which you are asked to plug in a value. In this question, you are given two definition equations and a nested function (a function within a function). You’re also told that m = 2. With nested functions, you start with the innermost equation and work outward, so begin by plugging 2 in for the variable in the circle equation: 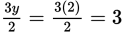. Now take the result, 3, and plug that into the square equation:

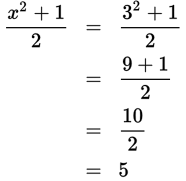
    The value of image is 5, so the correct answer is (D).

    Step 4: Confirm Your Answer

    When working with nested functions, remember to always work from the inside out. Doing so allows you to avoid trap choices like (C), which is the result of working from the outside in.

  2. (B)

    Step 1: Analyze the Question Stem

    Before beginning the solution, note for clarity that a positive digit is one of the integers 1, 2, 3, 4, 5, 6, 7, 8, and 9. You are given in the question stem that the product of the digits ⋄ and △ is • and that ⋄ > △. You want to know if there is sufficient information to determine the value of the digit ⋄.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) says that △ = 1. So the product of ⋄ and 1 is •. Because the product of any number and 1 is that number, the product of ⋄ and 1 is ⋄. So ⋄ = •. You know from the question stem that ⋄ > △, and because Statement (1) says that △ = 1, you have ⋄ > 1. However, you do not know the value of the digit. So ⋄ could be any of the eight remaining positive digits 2, 3, 4, 5, 6, 7, 8, and 9. Because there is more than one possible value for ⋄, Statement (1) is insufficient. Eliminate (A) and (D).

    Statement (2) says that • = 9. So the product of ⋄ and △ is 9. There are two ways to write 9 as the product of two digits, 9 × 1 and 3 × 3. Because ⋄ × △ = 9 and you must have ⋄ > △, it must be the case that ⋄ = 9 and △ = 1. So ⋄ has only one possible value, 9. Statement (2) is sufficient. (B) is correct.

  3. (E)
    Step 1: Analyze the Question

    You’re told that x ♦ y is defined by the expression 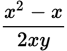 . Translated into English, this means that when you “diamond” two numbers, you square the first number, then subtract the first number from this square, and divide the result by 2 times the product of the first and second numbers. You also know that when y (the second number) equals 5 in this expression, the result is 2.

    Step 2: State the Task

    Determine the value of x based on the definition.

    Step 3: Approach Strategically

    Because you know that x ♦ 5 = 2, replace y with 5 in the defining equation and set it equal to 2: 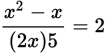. Combine factors in the denominator: 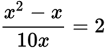. Next, multiply both sides by 10x: 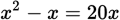 . Subtract 20x from both sides to yield x2 − 21x = 0. Now factor out an x from each term on the left: x(x − 21) = 0. Thus, either x = 21 or x = 0. The question stem specifies that x is positive, so you’re left with x = 21. The correct choice is (E).

    Step 4: Confirm Your Answer

    Check that you substituted numbers correctly into the definition and verify your calculations, making sure you solve for the value of x and not y. If you plugged in 5 for x and solved for y, you probably chose (A).

  4. (B)

    Step 1: Analyze the Question Stem

    The stem describes an operation performed on the variable x as ♫ x = ax − b(x − 1) + c, where a, b, and c are positive integers. The additional information that ♫ 0 = 7 is provided. Therefore, substitute 0 for x into the function and set it equal to 7: a(0) −b(0 − 1) + c = 7; this simplifies to b + c = 7. 

    Simplified, the question stem provides two variables but only one equation. Each additional value for ♫ x would enable you to create an equation in terms of a, b, and c, just as you did when you translated ♫ 0 = 7 into b + c = 7. So two more values for ♫ x or some other information that enables you to determine a value for c would be sufficient.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) says that a = 3. This information, unlike a value for ♫ x, does not enable you to write another equation, nor does a appear in the equation b + c = 7. Thus, Statement (1) is insufficient. Eliminate (A) and (D).

    Statement (2) informs you that c = 5. This information also does not enable you to write another equation, so you do not have enough information to determine the value of all the variables. However, you can plug this value into b + c = 7 to get the value of b. Therefore, Statement (2) is sufficient to solve for the value of b, and (B) is correct.