Answers and Explanations

Practice Set: Fractions and Decimals on the GMAT

  1. (B)

    Step 1: Analyze the Question Stem

    This is a Yes/No question. It is given that x and y are positive, so each side of the inequality can be multiplied or divided by x or y without having to flip the sign. The fractions can be eliminated by multiplying both sides by :  

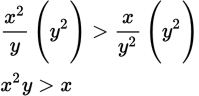
    This can then be simplified further by dividing both sides by x:

    Simplified this way, the question can be interpreted as asking whether the product of x and y is greater than 1.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) indicates that x divided by y is greater than 1. As y is positive, you can multiply both sides of this statement by y to get rid of the fraction:

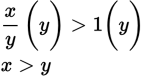
    However, knowing that that x is greater than y does nothing to confirm whether their product is greater than 1. It’s possible that x is 2 and y is 1, resulting in a product of 2. However, it’s also possible that x is 2 and y is 0.1, resulting in a product of 0.2. The product can be greater than or less than 1, making this statement insufficient. Eliminate (A) and (D).

    Statement (2) directly confirms that the product of x and y is indeed greater than 1. Thus, this is sufficient. Eliminate (C) and (E). 

    There is no need to combine the statements. The second statement is sufficient by itself, but not the first statement. The correct answer is (B).

  2. (D)

    Step 1: Analyze the Question Stem

    This is a Yes/No question. Because a and b are positive, both sides of the inequality can be multiplied or divided by either variable without having to switch the sign. Because the inequality can be rearranged in several ways, take a look ahead at the statements to determine what approach will be most useful. As each statement provides a different arrangement of the variables, it will be better to rearrange the given inequality twice, each time mimicking the arrangement in the statement being tested. 

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) provides information about the fraction , so manipulate the inequality in the question stem to get the same fraction for easier comparison. Start by dividing both sides by b:

    Then divide both sides by 8:

    As a decimal, . So the question is asking whether 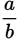 is  less than 0.375. If  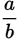is less than 0.374, as Statement (1) indicates, then it must also be less than 0.375. That makes Statement (1) sufficient. Eliminate (B), (C), and (E). 

    Statement (2) provides an inequality about b. Again, manipulate the inequality in the question stem to get b by itself for easier comparison. Divide both sides by 3 and translate the resulting fraction into a decimal:

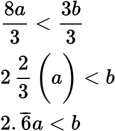
    So the question is asking whether b is greater than . If b is greater than 2.671a, as Statement (2) indicates, then it is certainly greater than . That makes Statement (2) sufficient. That eliminates (A).

    Combining the statements will not be necessary. Each statement is sufficient by itself, making (D) the correct answer.

  3. (D)
    Step 1: Analyze the Question

    The question states that four of the answer choices are equivalent to 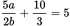  and one isn’t. Simplify that equation to make it easier to compare to the choices. There are a couple of routes you might take. You might first subtract   from both sides:  . So 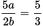. Cross multiply to get 15a = 10b. Then divide by 5 so that 3a = 2b. 

    Alternatively, you might have cleared the fractions first by multiplying each term by (2b)(3): 

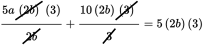
    15a + 20b = 30b

    15a = 10b

    3a = 2b

    Step 2: State the Task

    Determine which of the answer choices is not equivalent to the given equation. This means that the same values that produce an equality in the stated equation do not produce an equality for the correct choice.                              

    Step 3: Approach Strategically

    Rearranging the given equation in lots of different ways until you’ve satisfied yourself that it’s equivalent to four of the choices could be time-consuming. Fortunately, picking numbers will be an efficient approach. Since 3a = 2b, a = 2 and b = 3 would be good choices. 

    Because you’ve already simplified the given equation to 3a = 2b, you know that (A) is equivalent and is not the correct choice.

    (B): Since 5a − 2b = 5(2) − 2(3) = 10 − 6 = 4 and  this choice is equivalent to the original. Eliminate.

    (C): Plug the numbers into this equation:  . This also works. Eliminate.

    (D): 3a + 2b − 1 = 3(2) + 2(3) − 1 = 11, but 2a + 3b = 2(2) + 3(3) = 13. This is not a valid equation, so (D) is correct. 

    Since this is an EXCEPT question, there is no need to check (E). For the record, .

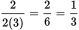    Step 4: Confirm Your Answer

    Confirm that your calculations for (D) are correct and that you chose an answer that is not a valid equation.

Practice Set: Exponents on the GMAT

  1. (C)
    Step 1: Analyze the Question

    This question states that after a machine’s wheel assembly turns 4.09 × 106 times, the machine needs maintenance. The machine has received maintenance 30 times.

    Step 2: State the Task

    Find the approximate total number of turns that the wheel assembly had made at the time of its last maintenance.

    Step 3: Approach Strategically

    Because the machine received maintenance 30 times, the total turns must be 30 times 4.09 × 106. Since the question asks for an approximate value, round 4.09 to 4. Notice that the answer choices are written in terms of powers of 10. Therefore, rewrite 30 as 3 × 10. Then calculate:

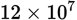
    Looking at the answer choices, notice that the leading value 12 is not among the options. However, 12 can be rewritten as 1.2 × 10, giving  (C) is correct.

    Step 4: Confirm Your Answer

    Reread the question stem, making sure that you translated the scenario correctly into math. For example, dividing 4.09 × 106 by 30 would result in (A). Also, make sure you accurately kept track of the exponent and the decimal places in your answer.

  2. (C)
    Step 1: Analyze the Question

    You need to solve for x in an equation with exponents in the numerator and denominator of a fraction. The bases in the numerator and denominator are not the same, but one of the bases, 8, is equal to the other one, 2, raised to the third power.

    Step 2: State the Task

    Because of the complexity of the expression with the variable and the potentially large values of the numbers, backsolving is unlikely to be efficient. Instead, use algebra and the rules for exponents to solve for x.

    Step 3: Approach Strategically

    Start by cross multiplying to eliminate the denominator of the fraction: 25x = (82x−2) × 8 = (82x−2)(81) = 82x−2+1 = 82x−1.

    Now the equation is 25x = 82x − 1. As written, the two bases are different, so it’s necessary to make them the same before solving for x. Since 8 = 23, you can substitute 23 for 8 in the equation: 25x = (23)2x−1. Further simplifying on the right yields 25x = 26x−3. 

    When exponential expressions with the same base have equal values, where the base is not 1, 0, or −1, the exponents must also have equal values. Therefore, 5x = 6x − 3, so x = 3. (C) is correct.

    Step 4: Confirm Your Answer

    Check that you properly multiplied exponents when converting the larger base to the smaller one. 

  3. (D)
    Step 1: Analyze the Question

    The question involves an expression that adds two numbers that have different bases and different exponents. Both exponents contain the variable x. Recall that you can only add or subtract numbers with exponents when both the bases and the exponents are the same.

    Step 2: State the Task

    Determine which of the answer choices is equal to the given expression.

    Step 3: Approach Strategically

    To solve this question algebraically, first convert both terms to a common base. Since 9 = 32, the expression becomes (32)x + 32x+1, which further simplifies to 32x + 32x+1. Now consider that 32x+1 can be restated as (31)(32x). Now the expression reads 32x + 3(32x), which is 4(32x ). (D) is correct.

    You could also use the picking numbers strategy. For a question with variables in the answer choices, all four incorrect choices must be eliminated because sometimes one or more incorrect choices will work for the particular value that you choose.

    Try x = 1. Then 9x + 32x+1 = 91 + 32+1 = 9 + 27 = 36. Now substitute 1 for x into each answer choice. Any choice that does not equal 36 when x = 1 can be eliminated.

    (A) 3(32x+1) = 3(33) = 34 = 81. Eliminate (A).

    (B) 34x−1 = 34−1 = 33 = 27. Eliminate (B).

    (C) 34x+1 = 35 = something greater than 81 of (A). Eliminate (C).

    (D) 4(32x) = 4(32) = 4(9) = 36. This could be the correct choice.

    (E) 122x = 122 = 144. Eliminate (E). 

    (D) is correct.

    Step 4: Confirm Your Answer

    Confirm that your application of the exponent rules and your calculations are correct.

Practice Set: Radicals on the GMAT

  1. (D)
    Step 1: Analyze the Question

    The question stem first says that . Translate each component of the next part of the sentence to arrive at the equation . Because you are being asked to find the value of x, look for a way to set the term with x in it equal to the numeric value on the right of the second equation. If , then . Now you have A2 equal to two different terms, so you can set them equal to each other: .

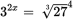    Step 2: State the Task

    Strategically apply exponent and radical rules to solve for x.

    Step 3: Approach Strategically

    If you happen to know that the cube root of 27 is 3 (because 33 = 27), then you can substitute 33 for 27 and simplify to . Because the bases are the same, you can set the exponents equal and solve: 2x = 4 and x = 2. 

    You can also use radical sign rules, which tell you that 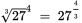. Then substitute 33 for 27 to make this . When you raise a power to a power, you multiply the exponents; , so the right side of your equation is 34. Now 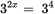,  2x = 4, and x = 2. 

    This matches choice (D).

    Step 4: Confirm Your Answer

    Backsolving is a great way to confirm your choice. Plug in 2 for x to find that A = 9 and therefore A2 = 81. This is indeed equal to 3 (the cube root of 27) to the fourth power. 

  2. (B)

    Step 1: Analyze the Question Stem

    This is a Yes/No question. Here you are given that r is positive, and you need to find out whether you have sufficient information to determine whether is an integer. There is no information in the question stem that you can use to determine whether or not 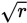is an integer, so look at the statements.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) says that r2 is an integer. If r = 4, then r2 = 42 = 16 is an integer, so Statement (1) is true. In this case, is an integer, and the answer to the question is yes. If r = 5, then r2 = 52 = 25 is an integer, so Statement (1) is true. In this case, 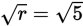is not an integer, and the answer to the question is no. Because different answers to the question are possible, this statement is insufficient. You can eliminate (A) and (D).

    Now look at Statement (2). If r = m2, where m is an integer, then 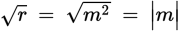. Thus, 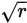must always be an integer, since you are told that m is an integer. Statement (2) is sufficient, so (B) is correct.

  3. (C)
    Step 1: Analyze the Question

    You are given a complicated radical expression with numbers but no variables.

    Step 2: State the Task

    Use the rules of radicals to simplify the given expression.

    Step 3: Approach Strategically

    Straightforward math is the best approach here. Subtraction under the radical sign cannot be “split up” under separate radical signs, so the first step is to combine the two terms into one fraction using a common denominator.

    Now simplify by finding the factors of 75 and 4 that are perfect squares. Since all that is left under the radical sign is multiplication and division, you can split up the factors to facilitate simplification. 

    The answer is , so (C) is correct.

    Step 4: Confirm Your Answer

    Check your application of the rules for radicals and your arithmetic. The GMAT will try to trick you into forgetting that you cannot split up subtraction and addition under the radical sign. Notice that (A) is the trap answer that awaits those who forget this rule.

Practice Set: Absolute Value on the GMAT

  1. (E)
    Step 1: Analyze the Question

    You are given an equation that has an absolute value. Recall that when absolute value is involved, you need to set up two equations, one for a positive value inside the absolute value bars and one for a negative value inside the bars. 

    Step 2: State the Task

    The question asks you to find what could be the value of x. This implies that x potentially has multiple values, although only one will be in the answer choices.

    Step 3: Approach Strategically

    First, deal with the term outside the absolute value bars by subtracting 2 from both sides of the equation to get |12 − 4x| = 4. Now, 12 − 4x could equal 4 or −4. Solve for each of the cases separately.

    If the expression equals 4, the equation is 12 − 4x = 4. Solve for the value of x:

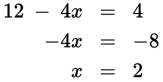
    Because this is not an answer choice, solve for the value of x when the expression equals −4: 

    This is choice (E).

    Step 4: Confirm Your Answer

    To confirm your answer, you can backsolve, plugging 4 in for x in the original equation: |12 − 4(4)| + 2 = |12 − 16| + 2 = |−4| + 2 = 4 + 2 = 6. (E) is confirmed as correct.

  2. (E)

    Step 1: Analyze the Question Stem

    This is a Yes/No question asking whether z = 0. Given the equation z = |x − 2| − |y + 2|, if z = 0, then |y + 2| = |x − 2|. So if the answer to the question is yes, x and y have the same magnitude but different signs. For example, if x = −2, y must equal 2 so that |2 + 2| = |−2 − 2| = 4. If x = 0, then y must equal 0 so that |0 + 2| = |0 − 2| = 2. So for sufficiency, the statements will need to provide enough information to determine whether x and y meet that condition. The question stem says that x and y are integers, so while the statements have inequalities involving scary fractions, you’ll only need to consider integer values in those ranges.

    Step 2: Evaluate the Statements Using 12TEN

    In Statement (1), the only integers in the range for x are 2 and 3, and the only integers in the range for y are −3 and −2. Thus, the values of x and y could, but do not necessarily have to be, opposites of each other. Eliminate (A) and (D).

    From Statement (2), you can conclude that x must equal 2 and that y must equal −3 or −2. Thus, y’s value could be but does not necessarily have to be the opposite value of x. Eliminate (B).

    Combining Statements (1) and (2), you know that x must equal 2 because that is the only value for x that works for both statements. However, in both statements, y could equal −3 or −2. Since y’s value could be −2 and the opposite of x, but y could also be −3, the correct answer is (E).

  3. (C)
    Step 1: Analyze the Question

    This question involves an inequality with an absolute value. The solution to an inequality will have a range of values, and solving for an absolute value means writing two inequalities, one if the value between the bars is positive and one if it is negative. Note that the question wants a statement that must be true, not one that could be true. 

    Step 2: State the Task

    Evaluate the inequality to find the range of values for j. Check this result against the answer choices to see which must hold true.

    Step 3: Approach Strategically

    Rewrite the given inequality as two inequalities: 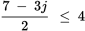 and 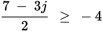. Remember to flip the inequality sign for the negative case. Evaluate both equations to find the range for j.

    Evaluate the first inequality. Reverse the inequality sign when dividing by a negative number.

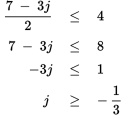
    Evaluate the second inequality:

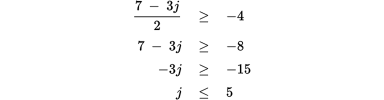
    Therefore, the full range of values for j is . 

    Evaluate the choices to see which must be true. (A) and (E) contain numbers that appear in the inequality for the full range of values for j, but both are incorrect because they use the opposite inequality symbols. (B) and (D) could both be true, but do not have to be true, as there are permissible values of j that are both less than and greater than . However, it is true that j must be less than 5, and (C) is correct.

    Step 4: Confirm Your Answer

    A good way to check your answer to questions involving inequalities is to sketch the solutions to the inequalities on a number line so you can see the range of the solutions. 

Practice Set: Inequalities on the GMAT

  1. (B)

    Step 1: Analyze the Question Stem

    In this Yes/No question, sufficiency means demonstrating that a is either definitely greater than 5 or that a is definitely less than or equal to 5.

    Step 2: Evaluate the Statements Using 12TEN

    Simplify Statement (1). If 8a ≥ 40, then a ≥ 5. This means that a can be greater than 5 or equal to 5, so this statement is insufficient. Eliminate (A) and (D).

    Statement (2) says that 4a + 6 ≤ 25, which simplifies to 4a ≤ 19 and a ≤ (19 ÷ 4). Since 19 ÷ 4 < 5, a must be less than 5. This means that the answer to the stem question is unequivocally no, so Statement (2) alone is sufficient. (B) is correct. 

  2. (C)
    Step 1: Analyze the Question

    The variable n is defined as an integer, and several operations are performed on n in the given inequality, which includes an absolute value expression.

    Step 2: State the Task

    Solve the inequality to determine n’s total possible number of integer values.

    Step 3: Approach Strategically

    Since each part of the inequality has a negative sign, start by multiplying each term by −1 to make it positive. Remember to reverse the direction of each inequality sign because you are multiplying by a negative number: 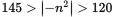. Also, this may be easier to read if you write it with the smallest value on the left, just as numbers are placed on the number line: . Now based on the general rule that |−x| = |x|, 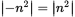, simplify the inequality further to .

    The question stem says that n is an integer, so  is a perfect square. Since 120 is 1 less than the perfect square 121 (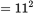) and 145 is 1 greater than the perfect square 144 (), both 121 and 144 are within the range of permissible values for . Therefore, you can rewrite the inequality as . Thus, the perfect square 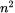 could equal only  or .

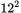    If ; if 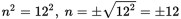. So n could equal ±11 or ±12 for a total of four possible values. Thus, (C) is correct.

    Step 4: Confirm Your Answer

    Ensure that you determined the entire total number of possible values for n, including the negative square roots of both 121 and 144.

  3. (E)

    Step 1: Analyze the Question Stem

    This is a Yes/No question that asks whether c is negative, given an inequality that contains c along with two other variables. That expression is positive, so (a − b) and c are either both positive or both negative. Thus, a statement that gives information on the sign of the expression (a − b) would provide sufficient information to answer the question.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) does not provide any information on c, so see what, if anything, you can deduce about a and b by rewriting Statement (1) to more closely resemble the (a − b) expression from the question stem.

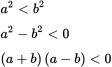
    Since the product of (a + b) and (a − b) is negative, either (a + b) is positive and (a − b) is negative, or (a + b) is negative and (a − b) is positive. The value of (a + b) is completely unknown, so you cannot determine whether (a − b) is positive or negative, and thus you don’t know whether c is positive or negative. Statement (1) is insufficient; eliminate (A) and (D).

    Statement (2) can be rewritten as follows.


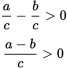
    Since this inequality matches that from the question stem, Statement (2) does not provide any new information and is thus insufficient. Eliminate (B).

    Now combine the statements. Since you already determined that Statement (2) just repeats what the question stem already says and that Statement (1) does not tell you the sign of either c or (a − b), the statements are insufficient even when combined. Thus, (E) is correct.