Answers and Explanations

Practice Set: Lines and Angles on the GMAT

(A)
Step 1: Analyze the Question

There are several relationships that you can deduce from the diagram:
1. Vertical angles are equal, so x + 2y = 5x − 4y.
2. Angles along a straight line add up to 180°, so x + 2y + 3x − 3y = 180.
3. By the same logic, 5x − 4y + 3x − 3y = 180.
Step 2: State the Task

The question only asks about the value of y. However, there are two variables, x and y, which means you need two equations to solve for the value of either individual variable.

Step 3: Approach Strategically

Any two of the relationships identified in the first step are sufficient to determine the value of y. For example, using the first two relationships, you can start by simplifying the first equation:

Simplify the second equation as follows:

Note that the 4x term appears in both simplified equations. Replace the 4x in the second equation with the 6y from the first equation and solve for y:

(A) is correct.

Alternatively, if you chose to use the first and third relationships, you can use the 6y = 4x relationship from simplifying the first equation and simplify the third equation as follows:

Note that 8x = 2 × 4x, which means you can replace it with 2 × 6y = 12y. Plug in 12y for 8x and solve for y:

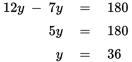
This again matches (A).

Another alternative is to use the two supplementary angle relationships. Based on the previous work, the two equations you have from simplifying the equations are 4x – y = 180 and 8x – 7y = 180. Double the first equation to yield 8x – 2y = 360 so that the x term has the same coefficient in both equations. Subtract the second equation from the first and solve for y:

Once more, (A) is correct.

Step 4: Confirm Your Answer

Make sure that you copied the expressions correctly from the figure and solved for the value of y, not x, which is (B) 54.
(C)

Step 1: Analyze the Question Stem

This is a Value question. You’re given a figure and told that lines r and s are parallel, which makes the other lines in the figure transversals. When a transversal intersects a pair of parallel lines, all acute angles formed by that transversal are equal, and all obtuse angles formed are equal. Therefore, since angle a and angle b are both acute angles on the same transversal, they’re equal to each other. So in order to determine the value of a + b, all you need to know is the value of either angle. Angles c and d form a straight line, so their sum is 180°.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) indicates that c − a = 25. This doesn’t give you enough information to pin down the value of any of the angles. Eliminate (A) and (D).

Statement (2) says that a − d = 15. Similar to Statement (1), this tells you that angle a is greater than angle d but gives no clue as to their values. Eliminate (B) and evaluate the statements together.

Restate the equation in Statement (2) as a = d + 15. Then substitute d + 15 for a in the equation in Statement (1) to get c − (d + 15) = 25, so c − d − 15 = 25 and c − d = 40. You know that c + d = 180. Add these two equations to eliminate the d terms:

You wouldn’t do the math for this Data Sufficiency question, but you could then determine that c = 110 and plug that into c − a = 25 to get the value of a. From that, you would also know the value of b, since a = b, and you could find the sum a + b. So, together, the statements are sufficient. (C) is correct.
(E)
Step 1: Analyze the Question Stem

Simplify the question stem by determining the number of degrees that the segment has to rotate to be less than 5% of its starting length. Consider picking 100 to represent the segment’s initial length, so when the segment is 5% of its starting length, its length is 5.
- After the first 45° rotation, the segment measures one-half of 100, or 50.
- After 90°, it measures 25.
- After 135°, it measures 12.5.
- After 180°, it measures 6.25.
- After 225°, it measures half of 6.25. This is less than 5.
The segment will therefore reach less than 5% of its starting length after moving five 45° increments, or 225°. Thus, the question becomes, “Did the segment make 5 movements?” or “Did it rotate 225°?”

Step 2: Evaluate the Statements Using 12TEN

Statement (1) says that the segment rotated at least 180°. If the segment rotated exactly 180°, the answer is no. However, the segment could have rotated 225°, and then the answer would be yes. Statement (1) is insufficient, so eliminate (A) and (D).

Statement (2) says that the segment made no more than 5 movements. If the segment made 5 movements, the answer is yes, but if the segment made fewer movements, the answer is no. Statement (2) is insufficient, so eliminate (B) and combine the statements.

Combining Statements (1) and (2) produces this statement: the segment rotated at least 180° and made at most 5 movements. This leaves open the possibility that it moved 4 times (for 180°) or 5 times (for 225°). The answer to the question could still be yes or no, so (E) is correct.

Practice Set: Triangles on the GMAT

(D)

Step 1: Analyze the Question

In this Roman numeral question, the figure consists of two triangles that share the side of length 5. One triangle’s other two sides measure a and b, while the other triangle’s other two sides measure y and z. Additionally, the latter triangle contains a right angle, so since z is opposite that right angle, z is that triangle’s hypotenuse, and y and 5 are that triangle’s legs.

Step 2: State the Task

This question asks which Roman numeral statement(s) could be true, meaning that incorrect answer choices reference statements that must be false.

Step 3: Approach Strategically

Roman numeral I says that sides a and b have the same length. Since you are not given any information for that triangle other than its remaining side’s length of 5, the lengths of a and b could be equal or unequal to each other. Since this statement could be true, eliminate those choices that do not contain Roman numeral I: (A) and (C).

Consider Roman numeral II and note that since z is the triangle’s hypotenuse and thus is that triangle’s longest side, z > y. Roman numeral II therefore must be false. Eliminate any remaining choices that contain II: (E).

Finally, examine Roman numeral III: . Recall the Pythagorean theorem: the sum of the squared leg lengths equals the squared hypotenuse length. So . Now subtract from both sides to obtain .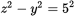

Since the two triangles share the side of length 5, see whether you could apply the Pythagorean theorem to the other triangle as well. While you are not told that the triangle with side lengths a and b is a right triangle, you are also not told that it cannot be. So if that triangle were a right triangle, you could treat the sides of lengths a and b as the triangle’s legs and the side of length 5 as that triangle’s hypotenuse to get . Since must equal and could equal as well, it could be true that 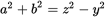. Since Roman numeral III could be true, (D) is correct.

Step 4: Confirm Your Answer

Ensure that you selected all choices that contain only Roman numeral statements that could be true.
(D)

Step 1: Analyze the Question

In this geometry question, you’re given a right triangle, and you’re told that BD bisects the hypotenuse of the triangle. This means that it also bisects ; that is, and both measure 45°.

Step 2: State the Task

Find the ratio of BC to AC, that is, the ratio of one of the legs of the original right triangle to its hypotenuse.

Step 3: Approach Strategically

Line segment BD divides right triangle ABC into two right triangles. Each of the two smaller triangles consists of a 90° angle at vertex D, a 45° angle at vertex B, and a 180° − (90° + 45°) = 45° angle at the third vertex. Thus, the angles at vertices A and C are 45°, and the large triangle is a 45-45-90 triangle. This means that the corresponding side ratios are . Leg BC is represented in this ratio by x and hypotenuse AC by , making the ratio of BC to AC equal to . Cancel the x terms and rationalize the denominator: .

Step 4: Confirm Your Answer

Make sure you answer with the ratio of the right sides in the right order. (E) is the reciprocal of the correct choice, reduced to its simplest form.
(C)

Step 1: Analyze the Question

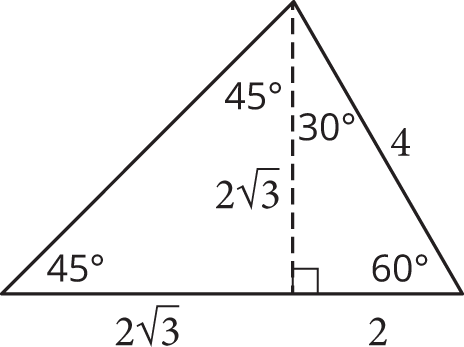
To find the area of a triangle requires knowing the base and height of the triangle. An angle measurement is missing from the diagram. Since all the angles in a triangle add to 180°, the missing angle must be 180° – (45° + 75°), or 60°. Note that two of the angle measurements, 60° and 45°, are part of two of the GMAT’s most commonly used shapes: the 45-45-90 special right triangle and the 30-60-90 special right triangle. If a special right triangle appears in a GMAT problem, it is probably key to the solution.

Step 2: State the Task

You are trying to find the area, which involves using a basic triangle formula: area = base × height.

Step 3: Approach Strategically

Divide the triangle into two smaller right triangles by imagining an altitude from the 75° angle to the horizontal base. This will create a 45-45-90 triangle on the left side of the altitude and a 30-60-90 triangle on the right side of the altitude.

The 30-60-90 triangle on the right side of the altitude has a hypotenuse of 4. The ratio of sides of a 30-60-90 triangle is , where x is the shorter leg, is the longer leg, and 2x is the hypotenuse. Therefore, you can deduce that the shorter leg is 2 and the longer leg (the altitude) is .

You now also know the length of the sides of the 45-45-90 triangle: . Therefore, the horizontal base of the large triangle is and the height is .

Now plug the known dimensions into the triangle area formula: area =. Therefore, (C) is correct.

Step 4: Confirm Your Answer

Check that you’ve correctly remembered the special right triangle relationships and have plugged in the correct values to the area formula.

Practice Set: Polygons on the GMAT

(B)

Step 1: Analyze the Question

You’re given a pentagon that has two parallel sides, three angles that are equal (labeled x°) and one angle of 60°. The remaining angle is labeled y°. This irregular pentagon is not a figure for which there is any set formula, so look to divide it into figures for which you do know formulas.

Step 2: State the Task

Use the given information to derive the value of y.

Step 3: Approach Strategically

Because two opposite sides of the pentagon are parallel, and you know one of the angles formed by one of these parallel sides, you can deduce the value of x, and from there, the value of y. Subdividing this complex polygon into simpler shapes can help with your analysis, and the 60° angle is a strong clue to make a 30-60-90 triangle. Draw an altitude to create this right triangle:

Because x is the complete angle at vertex A, you can deduce that x = 30° + 90° = 120°. Alternatively, you may have deduced this because AB and DE are parallel, making AE a transversal and the two angles it forms supplementary. Use this information to figure out how much all of the known angles add up to; then subtract this from the sum of interior angles of a pentagon to find y. The interior angles of a pentagon sum to 540°. (If you didn’t know this, you could use the formula for the sum of interior angles of a polygon: s = 180(n − 2), where s is the sum of interior angles and n is the number of sides.) Since x = 120°, 3x = 360°, and you can say that 3x + 60° = 420°. Therefore, y = 540° − 420° = 120°. That’s (B).

Step 4: Confirm Your Answer

Double-check that you’ve properly added up the angles and used the correct value for the interior angles of a pentagon.
(B)

Step 1: Analyze the Question

The question describes a contractor using half of her concrete to make an 8- by 12-foot rectangular area. She uses the remainder of the concrete to create a uniform-width walkway around that area. Since she used half the concrete to make the inner rectangle, she uses the remaining half—or the same amount of concrete—for the walkway.

Step 2: State the Task

Use the geometry formula for area of a rectangle to determine the maximum width of the walkway.

Step 3: Approach Strategically

Draw a sketch to illustrate the scenario:

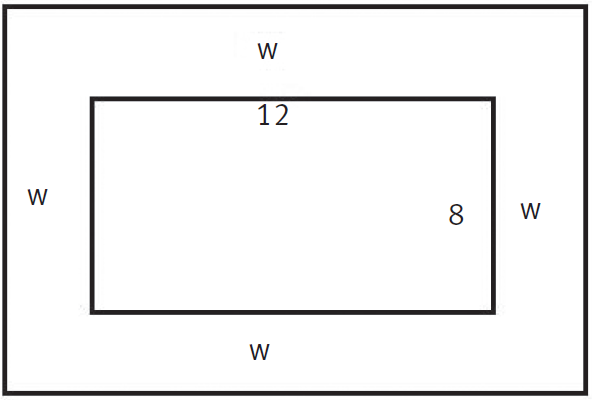
Since the amounts of concrete used for the base and the walkway are the same, the contractor will have enough concrete to make a walkway that has an area of 8 × 12 = 96 square feet. The area of the walkway is the area of the larger rectangle formed by the perimeter of the walkway less the area of the rectangular base. If you designate the width of the walkway as w, you can write the equation (w + w + 12)(w + w + 8) − (8 × 12) = 8 × 12, which simplifies to (2w + 12)(2w + 8) − 96 = 96. So 4w² + 40w + 96 = 192. Because the squared term has a coefficient of 4, see if you can divide all terms by 4 to eliminate that coefficient. Indeed you can, getting w² + 10w + 24 = 48. So in standard quadratic form, w² + 10w − 24 = 0. Factor this to get (w − 2)(w + 12) = 0. Since w cannot be −12 (a dimension of a geometric figure cannot be negative), it must be 2. (B) is correct.

Step 4: Confirm Your Answer

Given a width of 2, the outer dimensions of the walkway are 8 + 2 + 2 = 12 and 12 + 2 + 2 = 16. The area of such a rectangle is 12 × 16 = 192. This is, indeed, equal to the area of the monument base plus the area of the walkway, since 96 + 96 = 192.
(B)

Step 1: Analyze the Question Stem

This Yes/No question requires that you determine whether there is enough information to answer the question “Is the length of a side of square S greater than the length of a side of the equilateral triangle T?” Let a be the length of a side of square S and let b be the length of a side of equilateral triangle T. Then you can paraphrase the question as “Is a > b?” There is no information in the question stem that you can use to determine whether or not there is sufficiency, so look at the statements.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) says that a + b = 22. Here, a could be greater, b could be greater, or a and b could be equal. If a = 18 and b = 4 (they have to be consistent with Statement (1), so they must total 22), then a > b, and the answer to the question is yes. However, if a = 4 and b = 18 (again, consistent with Statement (1), as they total 22), then a < b, and the answer to the question is no.

Because different answers to the question are possible, Statement (1) is insufficient. Eliminate (A) and (D).

Statement (2): The ratio of the perimeter of the square to the perimeter of the triangle is 5 to 6. The perimeter of the square is 4a. The perimeter of the equilateral triangle is 3b. Thus, you can write the equation . Since this equation gives a proportional relationship between a and b, you know that you could simplify this equation and answer the question with a definite yes or no. Because a and b are side lengths, a and b are both positive, so this equation will describe a consistent ratio between these values. Note that you don’t have to solve for the ratio in order to know that Statement (2) is sufficient. (B) is correct.

Practice Set: Circles on the GMAT

(D)

Step 1: Analyze the Question

The question gives you the length of the arc formed by a 60° central angle. The ratio of the central angle to the total 360° of the circle can be used to relate the arc formed by the central angle to the full circumference.

Step 2: State the Task

Find the circumference of the circle and then use that value to determine the diameter.

Step 3: Approach Strategically

Set up a proportion to find the circumference:

Because circumference = π × diameter, 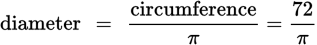. (D) is correct.

Step 4: Confirm Your Answer

Check your logic and the setup of the proportion. Be certain that you answered the question that was asked; (B) is the radius, not the diameter.
(C)

Step 1: Analyze the Question

The figure contains one circle inside a larger circle. Each of the tulip regions is a quarter of the inner circle. The total area dedicated to tulips is thus of the inner circle.

Each of the sunflower regions is a quarter of the ring between the outer and inner circles. The total area dedicated to sunflowers is of the ring area. The total area of the ring is the difference between the areas of the outer and inner circles.

Step 2: State the Task

Find the difference in areas dedicated to the two types of flowers, or the difference between half the ring area and half the inner circle area.

Step 3: Approach Strategically

First, find the area of the inner circle. The formula for the area of a circle is πr². From the question stem, you know that r = 3, so the area of the inner circle is πr² = π(3)² = 9π. Because the area in the garden for tulips is half of this, the tulip area equals .

Now solve for the area of the outer circle. The radius of the outer circle is AO, which is equal to AB + BO = 4 + 3 = 7. Therefore, the area of the outer circle is πr² = π(7)² = 49π.

Now you can solve for the area of the ring. This value is the difference of the two circle areas: 49π – 9π = 40π. Because the area in the garden for sunflowers is half of this, the sunflower area equals .

Lastly, solve for how much more area is dedicated to sunflowers by subtracting the tulip area from the sunflower area.

This matches (C).

Step 4: Confirm Your Answer

Confirm that you answered the right question, using the formulas for area of a circle (and not circumference, for example) and remembering to take half the various areas to get the areas planted with flowers.
(C)

Step 1: Analyze the Question Stem

This Value question says that two circles overlap and asks for that overlap’s area. To be sufficient, a statement needs to provide enough information to determine just one area value for the overlap.

Step 2: Evaluate the Statements Using 12TEN

Consider sketching the scenario that Statement (1) describes. The sample sketch below names the circles A and B.

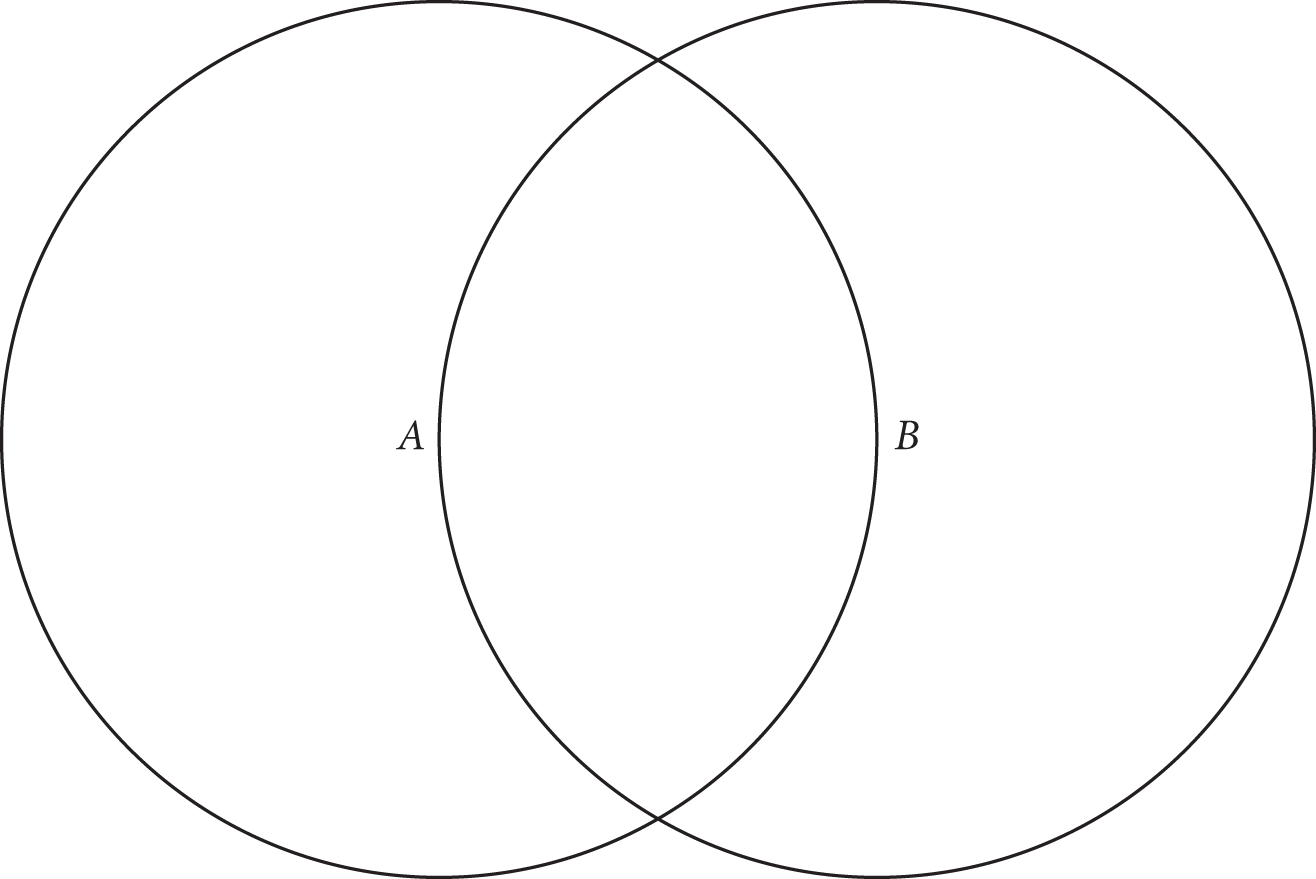
Since each circle’s edge intersects the other circle’s center, the circles must have the same radius. A small radius would mean small circles and a small area of overlap, while a large radius would mean large circles and a large area of overlap. Statement (1) is insufficient, so eliminate (A) and (D).

Statement (2) says that the circles’ circumferences add to 12π. Although you can determine a circle’s radius from that circle’s circumference, using the formula circumference = (2π)(radius), this statement tells you about both circles together, and there is no way to know whether they are congruent or one is larger than the other, or how much the two circles overlap. Therefore, finding the area of overlap is impossible. Since Statement (2) is insufficient, eliminate (B) and combine the two statements.

Statement (1) indicates that the circles are congruent and thus have the same radius. Statement (2) gives you the sum of the circumferences (12π), so dividing that total by 2 gives either individual circle’s circumference (6π). From the circumference, you could solve for the radius using the equation 6π = 2πr.

To determine whether knowing the radius is sufficient to answer the question, sketch radius AB and two additional radii for each circle (AD and AE for circle A and BD and BE for circle B) to create two congruent, equilateral triangles ADB and AEB that share segment AB as a base. An equilateral triangle has only 60° interior angles; the updated sketch below labels one as an example.

From this more complete sketch, notice that the area of overlap between circles A and B is (area of circle A’s sector DAE) + (area of circle B’s sector DBE) − (area of triangles ADB and AEB). Since the area of each triangle was originally included twice, once in the area of sector DAE and again in the area of sector DBE, their combined area must be subtracted once to leave the area of the two circles’ overlap.

Each of triangles ADB and AEB is equilateral, so the sum in degrees of angles DAB and EAB is 60 + 60 = 120; similarly, the sum in degrees of angles DBA and EBA is 120. Since 120° is one-third of the 360 total degrees in a circle, the area of each of sectors DAE and DBE is one-third of the area of circles A and B, respectively: 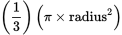. And since sectors DAE and DBE are congruent, the sum of their areas is double that of either area alone: .

The area of either triangle ADB or triangle AEB is determined by the triangle’s base and its height. Add heights CD and CE to triangles ADB and AEB, respectively.

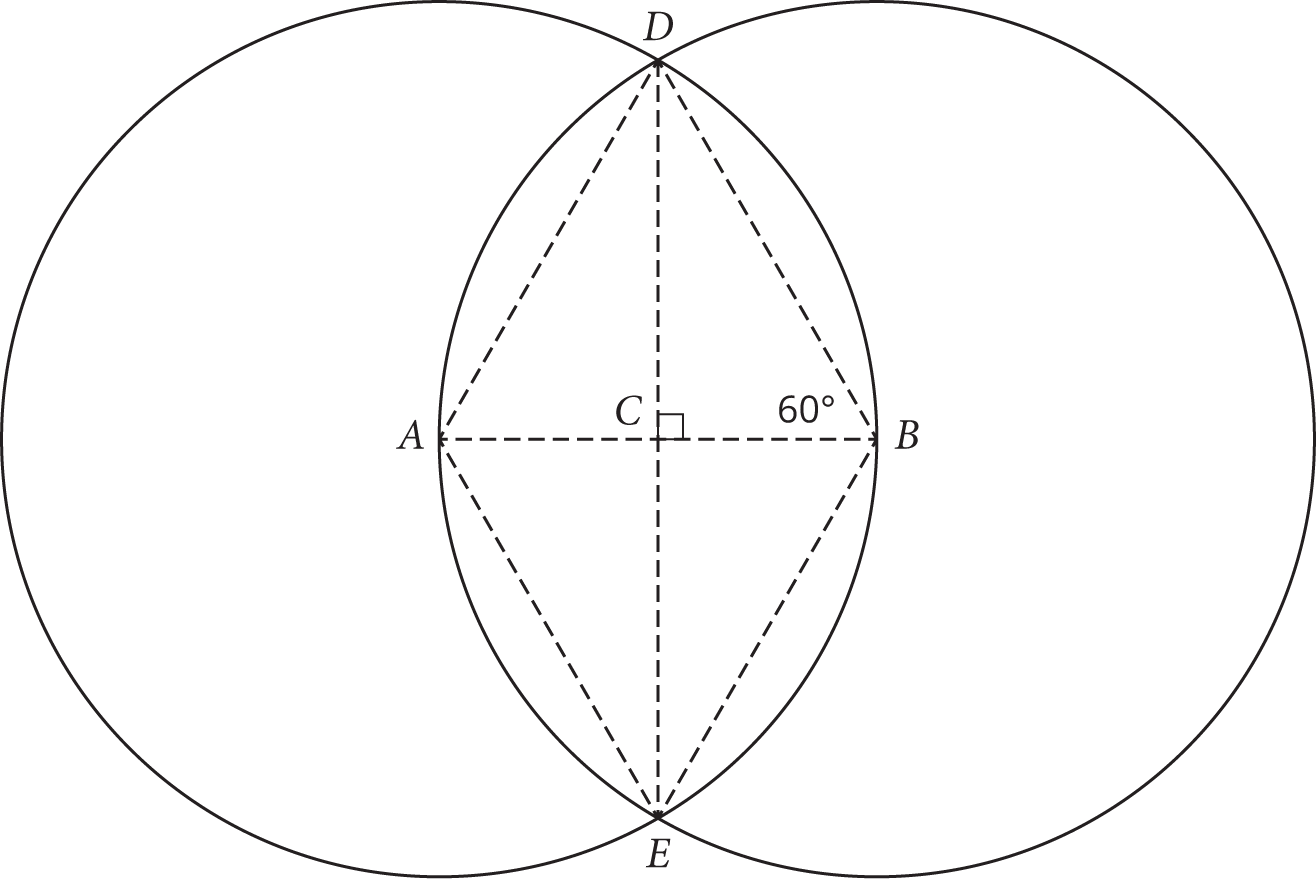
In sketching each equilateral triangle’s height, you break each triangle into a pair of congruent 30°-60°-90° triangles. The lengths of the sides opposite the 30°, 60°, and 90° angles are in the ratio . So for example, triangle DCB’s base CB is half of either circle’s radius AB and is multiplied by to determine that triangle’s height CD. Segment CD is also triangle ADB’s height, so that triangle’s area equals . Again, since triangles ADB and AEB are congruent, triangle AEB’s area is the same, so the sum of those triangles’ areas is twice their individual areas: .

Combining this information on the areas of the sectors and triangles, the area of the circles’ overlap is .

Since you know the radius from Statement (2), Statement (1) allows you to determine the area of the circles’ overlap via the expression. Since this is a Data Sufficiency question, do not spend time actually calculating that area; instead, knowing that you could if you wanted to is enough to conclude that (C) is correct.

Practice Set: Multiple Figures on the GMAT

(A)

Step 1: Analyze the Question Stem

For this Value question, you can make the following observations from the figure:

In triangle DFC, the measure of angle DFC is 180° − 70° − 60° = 50°.

Angle BFG is vertical to angle DFC, so the measure of angle BFG is also 50°.

In triangle FBG, the measure of angle GBF is 180° − 50° − 60° = 70°.

Angle ABF completes a straight line with angle GBF, so the measure of angle ABF is 180° − 70° = 110°.

Angles GFC and BFD each complete a straight line with angle DFC, so the measure of each of these angles is 180° − 50° = 130°.

There are many things that would give you the value of x. You have two of the angles in quadrilateral ABFD, so getting the measure of angle FDA would give you the third and allow you to solve for x (all quadrilaterals have interior angles that sum to 360°). It’s a complex figure, so there may be other ways to solve for x as well. You’ll need to think carefully about any information you’re given.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) states that AD is parallel to BC. Therefore, angle GBF and the angle marked x° must be equal. Because the measure of angle GBF is 70°, the measure of the angle marked x° must be 70°. Thus, x = 70. Statement (1) is sufficient. You can eliminate (B), (C), and (E).

Statement (2) tells you that ∠GBC = 70°. You already concluded that ∠GBF = 70° when you gathered information from the figure in step 1. Because angle GBF is the same as angle GBC, this statement does not provide you with any new information and is therefore insufficient.

The correct answer is (A).
(A)
Step 1: Analyze the Question

This question presents you with a complex figure consisting of three triangles inscribed in a semicircle. You are told that PQ is parallel to OS.

Step 2: State the Task

Find the measure of ∠ROS.

Step 3: Approach Strategically

The problem looks downright daunting, but the key, as with all geometry problems that involve complex figures, is to use any concrete information given to determine the starting point. With that in mind, begin by listing what you know from the figure:
1. Two of the three sides of each of the three inscribed triangles are radii of the semicircle. That means the three inscribed triangles are isosceles.
2. Since PQ is parallel to OS, QO is a transversal. When a transversal intersects with a pair of parallel lines, alternate interior angles are equal. In this case, since ∠PQO = 70°, ∠QOS must also be 70°.
Add this information to your sketch of ∆QOR and ∆ROS:

As you can’t simply split angle ∠QOS in half to find your answer (you can’t make assumptions about the relative sizes of angles just from eyeballing the diagram), you’ll instead need to solve for x. To do so, recall that a triangle’s interior angles sum to 180°. If you add up all six interior angles from ∆QOR and ∆ROS, you’ll have a sum of 360°. You can now set up an equation to solve for the value of x.

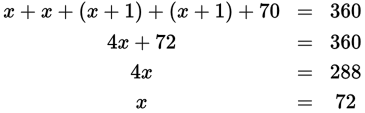
Since x = 72, each of the two base angles in ∆ROS is 72 + 1 = 73°. Therefore, the measure of ∠ROS is 180 − 2(73) = 180 − 146 = 34°. The correct answer is (A).

Step 4: Confirm Your Answer

If you were pressed for time, a bit of Critical Thinking would reveal that isosceles triangles with base angles of approximately 70° cannot possibly allow a remaining angle as large as (C), (D), or (E) would indicate.
(D)

Step 1: Analyze the Question

“An isosceles triangle is inscribed in a circle” means that each vertex of a triangle with at least two sides of equal length is on the circumference of a circle. Furthermore, “one of the triangle’s sides coincides with the circle’s longest chord” means that one side of the triangle is a diameter of the circle. When a side of a triangle that’s inscribed in a circle is a diameter of the circle, the vertex across from the diameter is a right angle, so the triangle is a right triangle and the side that coincides with the diameter is its hypotenuse. You’re also told that the measure of another side of this triangle is 5. Since the triangle is isosceles, the third side must also have a length of 5, and the angles that are opposite those sides must also be of equal measure. Since one angle already measures 90°, each of the other two measures 45°. Thus, the inscribed figure is a 45°-45°-90° triangle.

Sketching a figure on your notepad to visualize the figures will be helpful. Your sketch might look something like this:

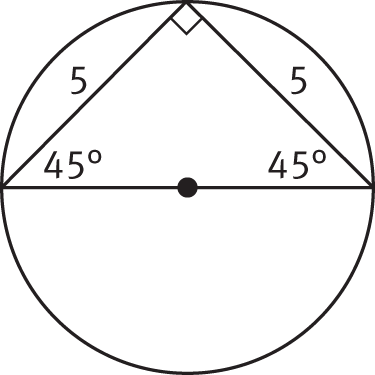
Step 2: State the Task

Determine the difference between the circle’s area and the triangle’s area, or A_C − A_T.

Step 3: Approach Strategically

You’re given a measure of one of the triangle’s sides, so start by finding the area of the triangle. Since it is a right triangle, one leg is the triangle’s base, and the other leg is the height. Substitute those lengths into the formula for area of a triangle: .

The formula for area of a circle is πr², so to find the area of the circle, you need to know the radius. In this figure, the radius of the circle is half the length of the triangle’s hypotenuse. Because the triangle is a 45°-45°-90° triangle, the measures of the sides are in the ratio . Thus, since each of the two legs measures 5, the hypotenuse measures . This is also the circle’s diameter, so the radius is half of , or 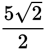. Thus, the circle’s area is this:

Finally, the area of the circle minus the area of the triangle is , which matches (D)—the correct choice.

On Test Day, if you were behind on time and needed to make a strategic guess, you could note that (A) stands out as being the only choice whose binomial factor doesn’t begin with π. Indeed, because π is greater than 1, 1 − π is negative. This choice is thus the product of a positive number and a negative number, which is negative. The difference between the area of a circle and the area of a triangle inscribed within it must be positive, so you could eliminate (A) and guess from among the other choices.

Step 4: Confirm Your Answer

Ensure that you answered the question, which asks for the difference in areas between the circle and the triangle. Potential trap answers include (A), which is the area of the triangle minus the area of the circle, and (C), which is the sum of the two areas.

Practice Set: Solids on the GMAT

(E)

Step 1: Analyze the Question

There are two cylindrical tanks. The first is completely full of gasoline, which is all transferred to the second. The height of the first tank is given. Both the height and the diameter of the second tank are given, but that height is actually irrelevant since you’re not finding the volume of the second tank; what is relevant is the height that the gasoline reaches in that second tank. The key to such a transference problem is noting that the volume of the gasoline in the original tank must equal the volume of the gasoline in the new tank.

Step 2: State the Task

Use the formula for volume of a cylinder to find the diameter of the original tank.

Step 3: Approach Strategically

The volume of any uniform solid is equal to the area of its base times that solid’s height, so the volume of a right circular cylinder is πr²h. More information is given about the second cylinder, so start there. It has a diameter of 24 feet, so its radius must be 12 feet. The gasoline fills it to a height of 2 feet, so use 2 for the height. Thus, the volume of the gasoline in that tank is π(12)²(2) = 288π ft³.

Now, plug this value back into the volume formula for the first cylinder to find its diameter: 288π = πr²(8), so r² = 36 and r = 6 ft. Finally, double the radius to find the diameter, which is 12 ft. The answer is (E).

Step 4: Confirm Your Answer

As always, be sure to read the question stem carefully, noting the key details. Here, the diameter, not the radius, of the second tank’s base was given and the gasoline did not reach the top of the second tank.
(D)

Step 1: Analyze the Question

The question stem tells you that the number of units in a rectangular solid’s volume and the number of units in that solid’s surface area are the same. Recall that the volume of a rectangular solid is Length × Height × Width and that the surface area is the sum of the areas of all six faces. You are also given specific values (4 and 5) for two of the three dimensions of the solid.

Step 2: State the Task

Determine the sum of the areas of the two largest faces of the solid.

Step 3: Approach Strategically

The solid’s volume and surface area are equal values, so . Since you are not told which dimensions 4 and 5 represent, simply substitute those values into this equation in a consistent way, assigning x to the third dimension. If, say, and w = 5, then 4(5)x = 2(4)(5) + 2(4)x + 2(5)x. Now, solve for x:

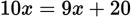
Because 20 is greater than 4 or 5, 20 is the largest dimension of the solid. Use that value and the second-largest dimension’s measure to find the area of each of the largest faces of the solid: 20(5) = 100. Finally, since opposite faces of a rectangular solid have the same area, double 100 to determine the sum of the areas of those two largest faces: 2(100) = 200.

The correct choice is (D).

Step 4: Confirm Your Answer

Ensure that you answered the question asked. For example, if you stopped working after solving for x, you might have selected (A). If you forgot to double the area in the last step, (C) was waiting for you.
(C)

Step 1: Analyze the Question

The question stem tells you that a cube with edge 6 contains the largest possible sphere that completely fits inside of it. So the length of the sphere’s diameter is the same as the length of the cube’s side. There is also some empty space in the cube that is not occupied by the sphere; this is the three-dimensional equivalent of inscribing a circle in a square—there’s some empty space in the corners. The formula for the volume of a sphere is given to you. Recall that the volume of a cube is the edge length cubed.

Step 2: State the Task

Determine the volume of the empty space in the cube, which is the difference between the cube’s and sphere’s volumes:

Step 3: Approach Strategically

You’re given concrete information about the cube, so start by finding its volume:

Now use the given formula to find the volume of the sphere. Since the length of the sphere’s diameter is the same as the length of the cube’s edge, the sphere’s radius is half the length of the cube’s edge: . Plug this in for r in the formula:

Now, determine the volume of the empty space in the cube: 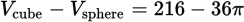. This doesn’t look like any of the answer choices, which all begin with a factor of 36. Factor 36 out of this expression to get 36(6 − π).

This matches (C), which is the correct choice.

Step 4: Confirm Your Answer

Make sure you determined the difference between the volume of the cube and the volume of the sphere and not some other value, starting with confirming that you correctly derived the sphere’s radius.

Practice Set: Coordinate Geometry on the GMAT

(C)

Step 1: Analyze the Question Stem

This is a Yes/No question asking whether two lines, each of which is represented by a unique equation, are parallel. Since two lines are parallel if they have the same slope, the statements are sufficient if they provide enough information to determine whether m and n, the slopes of lines 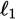and , respectively, are equal.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) says that m² − n² = 0. This is one of the “classic” quadratics; it factors to (m + n)(m − n) = 0. This means that m = n or −n. In other words, m and n have the same magnitude, but they could have either the same sign or opposite signs. So, if they had the same sign, the slopes would be equal and the answer to the question would be yes, but if they had opposite signs, the slopes would not be equal and the answer would be no. Thus, this statement is insufficient; eliminate (A) and (D).

Statement (2) says that the product of m and n is positive. This means that m and n have the same sign; they’re either both positive or both negative. Without more information, though, there’s no way to know whether they’re equal, so this statement is insufficient. Eliminate (B).

Now, combine the statements. According to (1), m = n or −n, but according to (2), m and n must have the same sign. That leaves m = n as the only possibility. Even though there’s not enough information to determine what the slopes are, they must be equal to each other. Choose (C).
(C)

Step 1: Analyze the Question

You’re given the x- and y-coordinates of one of the three vertices of triangle ABC, the x-coordinates of the remaining two vertices, and the area of the triangle. Since the y-coordinates of the two vertices not specified are both represented by y, they are the same, so the side BC of the triangle is parallel to the x-axis. Additionally, side AB lies on the y-axis, so this is a right triangle.

Step 2: State the Task

Determine the y-coordinate of points B and C on the graph.

Step 3: Approach Strategically

Since you are given the area of the triangle, use the formula for the area of a triangle to determine the missing coordinate:

The area of triangle ABC = 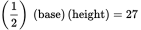. Since the graph indicates that the base of the triangle extends from point (0, y) to point (9, y), the base has a length of 9, so . Simplifying yields 9 × height = 54, so height = 54 ÷ 9 = 6. Since vertex A lies at point (0, 9), the y-coordinate of vertex B must be 9 − 6 = 3. Thus, y = 3. The correct choice is (C).

Step 4: Confirm Your Answer

Use the height you’ve calculated from the y-coordinate you’ve found to check whether the area matches that in the question stem. Note also that 6 in (E) is a trap answer for the unwary test taker, since that’s the height of the triangle, not the value of y.
(B)

Step 1: Analyze the Question

For any question involving the equation of a line, a good place to start is the slope-intercept form of the line, y = mx + b. Remember that if you have two points on a line, you can derive the entire equation, and if you have an equation of the line, you can calculate any points on that line.

Step 2: State the Task

You must solve for k, which is the amount by which the y-coordinate increases when the x-coordinate increases by 2.

Step 3: Approach Strategically

The slope of a line is the ratio between the change in y and the change in x. In other words, every time the x-coordinate increases by 1, the y-coordinate increases by the amount of the slope.

The equation of the line in the question stem is defined as x = 2y + 5. You must isolate y to have slope-intercept form:

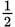So the slope of this line is . This means that for every change of +1 in the x direction, there is a change of + in the y direction. Therefore, you know that, because there is an increase of 2 units in the x direction when moving from m to m + 2, there must be a change of 1 unit in the y direction when moving from n to n + k. So k = 1.

Since there are variables that eventually cancel (m and n are not part of the answer choices), you can use picking numbers. Say that you choose the y-coordinate of the point (m, n) to be 0 to allow for easier calculations. Using the equation you’re given to relate x- and y-coordinates, you can calculate the x-coordinate:

So (m, n) is the point (5, 0).

Now you’ll plug your values of m and n into the next point: (m + 2, n + k). That yields (7, k). All you have to do is plug an x-coordinate of 7 into the equation to solve for k, the y-coordinate:

(B) is correct.

Step 4: Confirm Your Answer

Reread the question, making sure that you didn’t miss anything. For example, if you thought that the original equation was y = 2x + 5, then you would have answered (E). This step would help you to catch that error.