Answers and Explanations

Practice Set: Integers and Non-Integers on the GMAT

  1. (D)

    Step 1: Analyze the Question Stem

    This question gives an equation with three variables, each defined as a positive integer. It asks for the value of one of the variables.

    Before heading to the two statements, simplify the information in the question stem. Since each variable is a positive integer, dq is a positive integer. Since dq + r = 3, only two possibilities exist.  

    • If dq = 1, r = 2. In this case, both d and q must equal 1.
    • If dq = 2, r = 1. Here, either d = 1 and q = 2, or d = 2 and q = 1.

    So far, you have enough information to determine that d equals either 1 or 2. A statement that provides enough information to limit d to just one of those two values would be sufficient.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) essentially says that  is a fraction that is less than . For this to be true, r must be less than d, so r would equal 1 and d would equal 2. This statement is sufficient, so eliminate (B), (C), and (E).

    Statement (2) says that  is an integer that is less than 2. This means that , which can be rewritten as q = r. Now test the possibilities for q and r in relation to d: 

    • If q = r = 1, d = 2. 
    • If q = r = 2, the question stem’s equation becomes dq + r = 2d + 2 = 3, which would mean that d was not an integer—and this is not permitted according to the question stem.

    Therefore, d can equal only 2. This statement is sufficient, so (D) is correct.

  2. (B)

    Step 1: Analyze the Question Stem

    This Yes/No question states that f and g are positive integers and asks whether the fraction  is an integer. While multiplication, addition, and subtraction of integers all result in an integer, when an integer is divided by an integer, the numerator must be a multiple of the denominator for the result to be an integer. Thus, you need enough information to determine whether f + g is a multiple of f.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) informs you that g = 5f − 4. Substitute that into the fraction in the question stem to get  . This is an integer only if 4 is a multiple of f. There is not enough information to determine whether that is true, so eliminate (A) and (D).

    Statement (2),  , can be rearranged as 3f = g. Substitute that into the fraction to get  . This is, indeed, an integer, so (B) is correct. 

  3. (A)

    Step 1: Analyze the Question Stem

    This is a Yes/No question. You are told that n is a positive integer. You need to determine whether there is enough information to determine whether  is an integer. Since the square root of 9 is 3, in order for the answer to be yes, n would have to be 9 multiplied by a perfect square (a perfect square with 9 as a factor).

    To see this, you can pick numbers: 

    If n = 9 × 1, then . 

    If n = 9 × 4 = 36, then . 

    And if n = 9 × 9 = 81, then . 

    You can see that this pattern always yields an integer. 

    But if n = 3, , which is not an integer. If n = 9 × 3 = 27, then , which is not an integer. So if n is some number other than 9 multiplied by a perfect square, the answer to the question is no.

    Step 2: Evaluate the Statements Using 12TEN

    You can either use logic and the number property rules or pick numbers to evaluate the statements.

    Statement (1) tells you that   is an integer. This means that n = 3x, where x is some unknown integer that is a perfect square. If none of the factors of x is 3, then there is no way that n can be 9 times a perfect square, so the answer would be no. If, on the other hand, x does have a factor of 3, because x is a perfect square, it must have an even number of factors of 3. Consequently, n, which is 3x, would have an odd number of factors of 3 and its square root would not even be an integer, let alone an integer that is divisible by 3. Statement (1) is sufficient to answer the question with a no. Eliminate (B), (C), and (E).

    As an alternative to the above solution, you could have plugged in some numbers for n into . Use 9 × 1, 9 × 4, and 9 × 9, since those values mean that  is an integer. Plugging in 9 × 1 = 9 results in 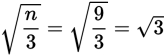, which is not an integer and, therefore, not a permitted value of n. Plugging in 9 × 4 = 36 gives you , and plugging in 9 × 9 = 81 results in 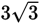. Continuing with greater values for n will just continue this pattern. None of the values that would answer the question with a yes are permissible values for Statement (1). Thus, the answer to the question must be no, and this statement is sufficient. 

    Statement (2) tells you that  is not an integer. For any value of n that is not a multiple of 14, that radical is not an integer. However, the question asks whether   is an integer. So n could be 9 and  would be an integer. On the other hand, there are a myriad of values for which neither  nor  is an integer. Eliminate (D). The correct choice is (A).

Practice Set: Odds and Evens on the GMAT

  1. (C)

    Step 1: Analyze the Question Stem

    This is a Value question. You need to determine whether there’s enough information to figure out how many of the integers in set S are even, and you know that the sum of all five integers in set S is odd. If the sum of the integers is odd, there has to be an odd number of odd integers in the set. Therefore, set S must contain either 1, 3, or 5 odd integers.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) says that the sum of A and B is odd. When two integers sum to an odd number, one must be even and the other odd (because the sum of two even integers or two odd integers will always be even). Therefore, there cannot be five odd integers in the set. Since A + B is odd, and the sum of all the integers in the set is odd, the sum of C, D, and E must be even. However, that could mean that two of these three are odd and one is even, or it could mean that all three are even. Thus, Statement (1) is insufficient. Eliminate (A) and (D).

    Statement (2) says that the product of B, C, and D is odd. An odd product can have only odd factors, never any even ones, so for B × C × D to be odd, B, C, and D must each be odd. However, this statement says nothing about A or E, which could both be even or both be odd for all five integers in the set to sum to an odd number. Therefore, this statement is insufficient and you can eliminate (B).

    Now take the statements together. You’ve already determined from information in the question stem and from Statement (1) that there must be either one or three odd integers in set S. From Statement (2), you know that B, C, and D are all odd. Thus, the two statements together prove that there must be exactly three odd integers in set S, and therefore two even integers. (C) is correct.

  2. (B)

    Step 1: Analyze the Question Stem

    In this Yes/No question, you are told that a is an odd integer and asked whether b is even. If you can answer either “definitely yes” or “definitely no” to this question, you’ll have sufficiency. Therefore, sufficiency means showing that b is either always even or always odd.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) provides an expression that’s even. Evaluate it one piece at a time. Since a is odd, a3 must also be odd (because odd × odd is always odd); therefore, a3 + 1 must be even (because odd + odd = even). Since an even times any other integer will always be even, b could be either even or odd and the statement would still hold true. Therefore, Statement (1) is insufficient. Eliminate (A) and (D).

    Statement (2) offers an algebraic equation that expresses the relationship between a and b. Solve this to see if there’s enough information to determine whether b is even or odd:

    There’s no need to simplify further. Instead, use the rules of odds and evens; since a is odd, again a2 must be odd, because odd × odd = odd. Thus, you can say that b2 − 4b must also be odd. Because any even number times any other integer is always even, 4b must be even. Therefore, you can say that b2 − even = odd. 

    Since an odd minus an even will always yield an odd, but an even minus an even will always be even, b2 must be odd. Because two integers multiplied together (in this case, b × b) that produce an odd product must both be odd, b itself must be odd. Thus, Statement (2) is sufficient, and (B) is correct.

  3. (E)
    Step 1: Analyze the Question

    In this abstract number properties question, m must be an odd number and p must be a prime number. A prime number is a positive integer with exactly two factors: 1 and itself. Examples of prime numbers include 2, 3, 5, and 7. Note that 2 is even (2 is the only even prime number), so p may be even or odd.

    Step 2: State the Task

    Determine which answer choice must always be odd or, in other words, eliminate any answer choices that can be even.

    Step 3: Approach Strategically

    For some number properties questions, picking numbers is an efficient strategy. 

    Since m is an odd number, let m be a small, easy-to-manage value such as 1. While 1 can be a poor choice for picking numbers in a Problem Solving question where you are solving for a numeric value, it is a fine choice when you are finding an expression with a particular number property, since 1 behaves the same way as any other odd number. Since p is a prime number, 5 is a good choice. Evaluate each answer choice by plugging in these values and eliminating any choice that produces an even value.

    (A) mp = (1)(5) = 5. Keep (A).

    (B) m(m + p) = 1(1 + 5) = 1(6) = 6. Eliminate (B).

    (C) m − p = 1 − 5 = −4. Eliminate (C).

    (D) m2 + 2p2 + 1 = 12 + 2(5)2 + 1 = 1 + 50 + 1 = 52. Eliminate (D).

    (E) m2(m + 2p) = 12(1 + 2 × 5) = 1(1 + 10) = 1(11) = 11. Keep (E).

    Since both (A) and (E) produced odd values, they both can be odd. But must they be odd? Pick numbers one more time. Pick 2 for p to test an even number for this variable. Keep m = 1 since all other permissible values for m are also odd and will not affect the result.

    (A) mp = (1)(2) = 6. Eliminate (A).

    Therefore, (E) is correct. 

    Step 4: Confirm Your Answer

    You can verify that (E) is correct: m2(m + 2p) = 12(1 + 2 × 2) = 1(1 + 4) = 1(5) = 5. Also, you can check (E) by applying the rules for odds and evens. Since m2 is an odd value squared, this is an odd × odd, which is always odd. Then 2p is even for any p value, and m + 2p is then an odd + even, which is odd. Lastly, multiplying two odd values, m2 and m + 2p, yields an odd product. 

Practice Set: Positives and Negatives on the GMAT

  1. (C)
    Step 1: Analyze the Question

    You know that x – y = 8. As this is a Roman numeral question with variables, expect to use picking numbers and don’t forget to check the Roman numeral statements in the most efficient order. In this question, begin with Statement II, as it shows up the most in the answer choices.

    Step 2: State the Task

    Determine which of the Roman numeral statements are true.

    Step 3: Approach Strategically

    Statement II: If x is positive, y must be positive. To test whether this statement needs to be true, try to pick some numbers for x and y where the result is false. The key is to pick numbers such that the condition is true but the result is false. If x = 6 and y = −2, then x – y does equal 8. The condition is true, yet you were able to make the result false, so Statement II does not need to be true. Eliminate (B), (D), and (E).

    Of the remaining statements, Statement I (Both x and y are positive) is the easier one to test because the numbers picked for x and y can be used to invalidate this statement as well. Eliminate (A).

    Therefore, the correct answer is (C).

    Step 4: Confirm Your Answer

    Confirm the answer by checking Statement III: If x is negative, y must be negative. In the equation x – y = 8, if x is negative and y is positive, then the result would simply get more negative. The only way to arrive at a positive answer when x is negative is for y to also be negative. Choice (C) is confirmed.

  2. (B)
    Step 1: Analyze the Question

    The question tells you that 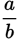 is a fraction between −1 and 1. The answer choices compare various expressions to 0, so you’ll be considering positive and negative number properties as you evaluate the choices. The inequality in the question stem means that the absolute value of a is less than the absolute value of b (a is closer to 0); the two values may have the same or different signs. 

    Step 2: State the Task

    Find the answer choice that cannot be true, no matter what permissible values of a and b are used.

    Step 3: Approach Strategically

    Evaluate each choice to see whether or not it can be true; since there’s no need to go in order, pick statements that seem easy to evaluate. (A) and (E) are very similar and relatively easy to evaluate. Since both a and b could be negative, their sum could be less than 0, which means (A) could be true; since they could be positive, their sum could be greater than 0, which means (E) could be true. Eliminate both of these choices.

    (C) is a good one to tackle next. This statement is true if a > b. The inequality in the question stem allows for a to be positive while b is negative (e.g., a = 1 and b = −2), so this choice could be true—eliminate it.

    (B) and (D) contain the same quadratic expression: (a + b)(a − b). Restate this as a2 − b2. Any non-zero value raised to an even exponent is positive, so the fact that a and/or b could be negative can be ignored. The absolute value of b is greater than that of a, so b2 > a2. Thus, a2 − b2 must be negative and cannot be positive. The statement (a + b)(a − b) > 0 cannot be true, so (B) is correct.

    Step 4: Confirm Your Answer

    If needed, you can pick permissible numbers to quickly check that (B) cannot be true. 

  3. (D)

    Step 1: Analyze the Question Stem

    This is a Yes/No question that asks whether an algebraic expression is negative. The answer will be yes if (s − t) and st have opposite signs, and the answer will be no if they have the same sign. Thus, a statement would need to provide the values of the individual variables or the signs of both (s − t) and st to provide sufficient information to answer the question.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) says that s is positive and t is negative. Therefore, (s − t) involves subtracting a negative number from a positive number. Subtracting a negative number is the same as adding a positive number, so since s is already positive, (s − t) is really a positive number plus another positive number, which must be positive. 

    Additionally, st is a positive number times a negative number, so st is negative. So . The answer to the question is thus a definite yes, and Statement (1) is sufficient; eliminate (B), (C), and (E).

    Statement (2) says that the reciprocal of the given expression is less than −1. Whether a negative fraction is written as or as , the fraction is still negative. So  is also negative, making Statement (2) sufficient; (D) is correct.

Practice Set: Factors and Multiples on the GMAT

  1. (C)
    Step 1: Analyze the Question

    The question states that a number is divisible by both 18 and 24, meaning that 18 and 24 divide into the number with no remainder. This is the same as saying that this number is a multiple of both 18 and 24. 

    Step 2: State the Task

    By asking which choice the number is “divisible by,” the question is asking which of the choices divides into the number with no remainder. This is the same as asking which of the choices must be a factor of the number.

    Step 3: Approach Strategically

    To think about what this number could be, you can count by 18s and 24s until you find a number that is on both lists. So it’s 18, 36, 54, 72 . . . and it’s 24, 48, 72 . . . The smallest number that’s divisible by both 18 and 24 is 72. Numbers smaller than this aren’t divisible by both 18 and 24, and while the number could be a larger multiple of 72 (for example, 2 × 72 = 144 is divisible by both 18 and 24), it isn’t necessarily greater than 72. Thus, you know that the number must be divisible by 72, and (C) is correct. Note that 72 is the least common multiple of 18 and 24.

    If you don’t feel comfortable counting by 18s and 24s (or if you encounter a problem with larger numbers that you definitely don’t feel comfortable counting by), another way to find the least common multiple is to use prime factorization, discussed in depth in the next section. The prime factorization of 18 is 2 × 3 × 3, so this number must have at least one 2 and two 3s as factors. The prime factorization of 24 is 2 × 2 × 2 × 3. You already know the number has a 3 as a factor (in fact, it has two 3s), but now you also know it must have not just one but three 2s as factors. So the number in question must have prime factors of 2, 2, 2, 3, and 3. It could have other factors as well, but these are the only ones you can be sure of.

    If you go the prime factorization route, the next step is to determine the prime factors of each choice and compare them to the prime factors 2, 2, 2, 3, and 3. The prime factors of 30 are 2, 3, and 5, but the number does not necessarily have a prime factor of 5. Eliminate (A). The prime factorization of 36 is 2 × 2 × 3 × 3. Since the number in the question requires three factors of 2, eliminate (B). The prime factorization of 72 is 2 × 2 × 2 × 3 × 3. All of these prime factors must be in the given number, so (C) is correct. 

    Step 4: Confirm Your Answer

    Be certain that you answered the question that was asked. A common error is to multiply 18 by 24 to get 432 and choose (E). However, while it is possible that the number is 432 or a multiple of 432, it does not have to have all these factors; it could be a smaller common multiple of 18 and 24.

  2. (C)
    Step 1: Analyze the Question

    This question states that 96x can be a factor of 8110+x. Because x is a positive integer, both exponent terms are positive integers. The answer choices are possible values of x.

    Step 2: State the Task

    Use the rules of exponents and an understanding of factors and multiples to find the largest possible exponent x that will make 96x a factor of 8110+x. 

    Step 3: Approach Strategically

    First, to work more easily with the two exponent terms, give them the same base. Since 81 is 92, 8110+x is (92)10+x = 920+2x. 

    Now the task is to find the largest x such that 96x is a factor of 920+2x. Recall that the largest factor of a positive integer is that integer (e.g., the greatest factor of 5 is 5, and the greatest factor of 100 is 100). So the largest factor of 8110+x is a value equivalent to 8110+x. Therefore, find the x value that makes 96x equal to 920+2x. Since the bases are the same, set the exponents equal to each other and solve for x.

    6x = 20 + 2x

    4x = 20

    x = 5

    When x = 5, 96x equals 8110+x and is its greatest possible factor. (C) is correct. 

    Step 4: Confirm Your Answer

    Plugging 5 back in for x shows that the two exponent terms are equal. You get 96×5 and 8110+5, or 930 and 8115. Because 81 = 92, 8115 = (92)15 = 930. The two values are equal, and 96x is as large as it can be to still be a factor of 8110+x; x can’t be any greater than 5.

  3. (D)
    Step 1: Analyze the Question

    This question involves multiples of 3 and multiples of 4 or, in other words, numbers that are divisible by 3 or by 4. When dealing with divisibility, remember that prime factorization can often provide an efficient path to the solution.

    Step 2: State the Task

    Find the number of multiples of 3 that are less than 70 and take out the values that are multiples of both 3 and 4. Find the number of multiples of 4 that are less than 70 and take out the values that are multiples of both 3 and 4. Add the two values together.

    Step 3: Approach Strategically

    The prime factorization of 3 is 3 because it is already a prime number. The prime factorization of 4 is 2 × 2. Since there are no overlaps in the prime factors needed to make up the two numbers, a number that is a multiple of both 3 and 4 is a multiple of 2 × 2 × 3 = 12.

    Dividing 3 into 70 yields 23 and a remainder. Therefore, there are 23 multiples of 3 among the positive integers less than 70. Dividing 12 into 70 yields 5 and a remainder, which means there are 5 positive integers less than 70 that are multiples of both 3 and 4. Subtracting 5 from 23 yields 18, which represents the number of positive integers less than 70 that are multiples of 3 but not 4.

    Dividing 4 into 70 yields 17 and a remainder. Therefore, there are 17 multiples of 4 among the positive integers less than 70. You have already found that there are 5 positive integers less than 70 that are multiples of both 3 and 4. Subtracting 5 from 17 yields 12, which represents the number of positive integers less than 70 that are multiples of 4 but not 3.

    The question asks for the number of multiples of 3 or 4 but not both. This is equal to the number of multiples of 3 but not 4 plus the number of multiples of 4 but not 3, the two values previously computed. Adding 18 and 12 yields 30, making (D) correct.

    Step 4: Confirm Your Answer

    To confirm the answer, you could write out all of the multiples of 3 under 70, then cross out any that are multiples of 4. Next, write out all the multiples of 4 under 70 and cross out any that are multiples of 3. The total number of numbers that are not crossed out is 30, so (D) is confirmed.

Practice Set: Remainders and Primes on the GMAT

  1. (B)

    Step 1: Analyze the Question Stem

    This Yes/No question states that n is an integer between 12 and 24 inclusive, and it asks whether n is a prime number. Information that allows you to determine that n definitely is prime, or definitely is not prime, will be sufficient.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) tells you that dividing n by 4 leaves a remainder of 1, meaning that n is 1 greater than a multiple of 4. The multiples of 4 within the range are 12, 16, 20, and 24, and 1 more than 24 is outside the range. Thus, the possible values of n are 13, 17, and 21. The first two are, indeed, prime numbers, but 21 is divisible by 3 and 7. Therefore, Statement (1) is insufficient. Eliminate (A) and (D).

    Statement (2) says that dividing n by 6 leaves a remainder of 1. Thus, according to this statement, n could be 13 or 19. Both of these are prime numbers, so Statement (2) is sufficient. (B) is correct.

  2. (A)
    Step 1: Analyze the Question

    The question gives the values of x and y and says that x2y2 is the product of three integers and a third variable, z. You need to determine the value of z. When the GMAT presents large-scale multiplication or division that seems overly complicated, look for a faster way. This question is a great candidate for prime factorization, since you need to factor a large product to determine the unknown factor z.

    Step 2: State the Task

    Determine the prime factors of the given expression and of each term in the product; then cancel out all the common terms. Those that remain will be the prime factors of z.

    Step 3: Approach Strategically

    Find the prime factorization of x2 and y2:

    Thus, you can say that x2y2 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5 × 7 × 7. Now find the prime factors of 21, 28, and 30:

    Therefore, 21 × 28 × 30 × z = 2 × 2 × 2 × 3 × 3 × 5 × 7 × 7 × z. Now compare the two lists of prime factors you’ve found and cancel out prime factors that are shared to determine what is left over; these will be the factors of z:

    (A) is correct.

    Step 4: Confirm Your Answer

    When using prime factorization, be careful to list all of the prime factors, including ones that repeat, such as 2 × 2 × 2 × 2 or 5 × 5.

  3. (A)
    Step 1: Analyze the Question

    This question tests your ability to think critically about the characteristics of remainders in division.

    Step 2: State the Task

    Use the two equations given to find the remainder when a + b is divided by 5.

    Step 3: Approach Strategically

    Start by determining the value of a + b by adding the two given equations: a + b = 5m + 2 + 5n + 13 = 5m + 5n + 15. Notice that all three terms have a common factor of 5, so a + b = 5(m + n + 3). Thus, (a + b) ÷ 5 = m + n + 3. Since m and n are integers, m + n + 3 must be an integer. So when a + b is divided by 5, the result is an integer; this means that a + b is a multiple of 5. Since a + b is a multiple of 5, there is no remainder when a + b is divided by 5, and (A) is correct.

    Step 4: Confirm Your Answer

    To double-check your work, you could pick numbers. Using 2 for m and n will make the arithmetic easy. Now a = 5(2) + 2 = 12 and b = 5(2) + 13 = 23. Thus, a + b = 12 + 23 = 25, which is evenly divisible by 5.