Answers and Explanations

Practice Set: Ratios on the GMAT

1. (C)

   Step 1: Analyze the Question

   The question gives you enough information to set up two ratios. The football program gets 4 times as much funding as basketball, so the ratio f:b is 4:1. Football and basketball combined get 3 times as much funding as the other sports, so the ratio (f + b):s is 3:1. However, no actual values are given.

   Step 2: State the Task

   Find the ratio of basketball’s funding to funding for other sports (not including football).

   Step 3: Approach Strategically

   Picking numbers is a great strategy to answer ratio questions when no actual values are given. Numbers need not be realistic; pick easy-to-use values. Let the funding for basketball be $3. Since football receives 4 times as much, its funding is $12. Together, these two programs have $15 in funding, which is 3 times as much as that of all of the other sports combined. Therefore, the other programs receive $5. Finally, the ratio of funding for basketball to that for all other sports is 3:5.

   Alternatively, select variables to represent the funding unknowns (such as f for football, b for basketball, and s for other sports programs). Then, f = 4b, since football gets 4 times more than basketball. Together, these two teams’ funding is f + b, and, substituting 4b for f, the total amount is 4b + b = 5b. That’s 3 times the amount given to the other programs, s, so 5b = 3s. Rewriting the equation to solve for b:s, you obtain the ratio 3:5.

   Solving with either method shows that the correct answer is (C).

   Step 4: Confirm Your Answer

   In a ratio question where the answer represents a part:part ratio, make sure the answer you pick represents the right parts in the right order.

2. (A)

   Step 1: Analyze the Question Stem

   This Value question stem provides a proportion with four variables and asks for a numerical value of the ratio of b to d. Rearranging the proportion to put b over d on one side may help you visualize what is needed: cross multiply to get ad = bc; divide both sides by d to get 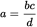, and divide both sides by c to get 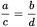  . Therefore, you need the ratio of a to c in order to determine the ratio of b to d. 

   Step 2: Evaluate the Statements Using 12TEN

   Statement (1) says that  . Cross multiply to find that 2ab = 3bc. Divide both sides by b: 2a = 3c. This means that  . You’ve already determined that this is also the ratio of  . This statement is sufficient, so eliminate (B), (C), and (E).

   Plug the values in Statement (2) into the equation: 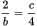 . Cross multiplying results in bc = 8. Although the statement provides a value for d, you can’t determine the value of b, so this statement is insufficient. (A) is correct.

3. (A)

   Step 1: Analyze the Question

   You are given two ratios, a to b and b to c, and are asked to solve for the ratio of a to c.

   Step 2: State the Task

   Produce the ratio a to c. You can do so by picking numbers or by translating the given information into equations and combining them.

   Step 3: Approach Strategically

   Translating the first equation, you have .

   Translating the second equation, you have .

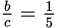   You can calculate by multiplying by :

   

   (A) is correct.

   Had you used picking numbers, the most straightforward values to choose are a = 4 and b = 3. If b = 3, then the only permissible value of c is 15. That makes the ratio of a to c equal to .

   Step 4: Confirm Your Answer

   When you are given two ratios, their product or quotient will always produce a third ratio. Be sure to confirm the order of the words in the question stem ratios to ensure that you have translated the ratios correctly.

Practice Set: Applying Fractions to Proportions on the GMAT

4. (B)

   Step 1: Analyze the Question

   The first sentence of the question, with “directly proportional,” is a strong clue that you can set up an equation to relate the length of the cable to its weight.

   Step 2: State the Task

   Create a proportion using the known length-to-weight relationship to find the weight of 110 meters of the cable.

   Step 3: Approach Strategically

   Let w equal the unknown weight of 110 meters of the cable. The cable’s weight is proportional to its length, so set up a proportion:

   

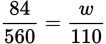
   While it’s important to know how to calculate such proportions mathematically, using critical thinking and estimation can often make your life easier on Test Day. 

   Note the relationship between 560 and 110: 110 is about a fifth of 560 (that’s because 110 × 5 = 550, which is very close to 560). Therefore, you can say that the unknown weight of 110 meters of cable must be about a fifth of 84. A fifth of 100 would be 20; a fifth of 75 would be 15; a fifth of 84 must be between 15 and 20. Among the answer choices, only 16.5 is close to one-fifth of 84. Thus, (B) is correct.

   If you didn’t spot this opportunity to estimate, you could do the math like this: 

   

   Step 4: Confirm Your Answer

   Plug the value you calculated for w back into the original proportion you set up to confirm that the relationship among values makes sense.

5. (A)

   Step 1: Analyze the Question

   You’re given a ratio of length of a plank to cost of that plank. You’re also told the lengths of two planks that will be purchased. You can express this ratio as a fraction and reduce: . 

   Step 2: State the Task

   You’re asked for the difference between the two people’s costs. Use the fixed (proportional) relationship between length and cost to find the cost of the difference between their planks.

   Step 3: Approach Strategically

   The plank that Jordan wants to buy is 10 – 7.5 = 2.5 feet longer than the plank that Kristen wants to buy. Let x be the cost of the 2.5-foot difference and set up the following proportion:

   

   The equation after you cross multiply is x = 16 × 2.5, so x = 40. (One way to do this mental arithmetic efficiently is to first multiply 16 by 2 to get 32, then multiply 16 by 0.5 to get 8, and finally to add 32 and 8 to get 40.)

   This matches (A).

   Step 4: Confirm Your Answer

   You can confirm your answer by solving for the separate amounts that Jordan and Kristen pay and then taking the difference. Since they pay $16 per 1 foot, Jordan pays 10 × $16 = $160 and Kristen pays 7.5 × $16 = $120. That’s a difference of $40.

6. (C)

   Step 1: Analyze the Question

   This question presents colored chips as parts that make up a whole. Most of the parts are identified as fractions of the whole, while one part is identified as a specific quantity. If you note that the actual number of each color of chips as well as the total number of chips must be integers, this insight will help you backsolve efficiently. (Things that normally come whole, such as chips, people, pets, etc., will never be broken into pieces in proportions questions on the GMAT.)

   Step 2: State the Task

   Use the information given about chips of different colors to determine the total number of chips. 

   Step 3: Approach Strategically

   There is more than one way to approach this question. One strategy is to determine what fraction of the total are the 12 red chips and then use that information to calculate the total number. Convert the three given fractions to the common denominator of 30 and add those rewritten fractions: 

   

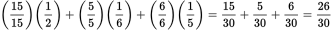
   So the rest of the chips, , are the 12 red ones. Solve for the total number of chips, x, by setting up the proportion of part-to-whole ratios, . Cross multiply: 2x = 180. Thus, x = 90, and (C) is correct.

   Alternatively, you could backsolve. Since 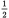, , and of the chips are integers, the total number of chips must be divisible by 2, 5, and 6. Thus, the total is divisible by the least common multiple of 2, 5, and 6, which is 30. Since the total number of chips must be divisible by 30, eliminate (B), (D), and (E). Select one of the two remaining choices to backsolve. For (A), 60, there would be  white chips, 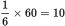  green chips, and   blue chips. Thus, 60 − 30 − 10 − 12 = 8 chips would be red if 60 were the correct total. Since there are actually 12 red chips, the correct choice must be (C), 90.

   Step 4: Confirm Your Answer

   As a quick check that you determined the correct total, use the fact that when a fraction is taken of a whole, the fraction is multiplied by the whole. Thus, multiply the fractions given in the question stem by 90 and then sum those values along with the 12 red chips. The result should equal 90: 

   
   

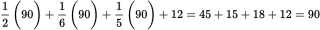
Practice Set: Percents with Specified Values on the GMAT

7. (B)

   Step 1: Analyze the Question

   The question provides the percentage of gravel in four different batches of concrete that are combined into one large mixture. Batch A weighs 1,000 pounds. The weights of the other batches are given in relative terms. Batch B is twice the weight of batch A, or 2,000 kilograms. Batch C weighs 25% less than batch B, so batch C is 1,500 kilograms. Batch D is half the weight of batch A, or 500 kilograms.

   Step 2: State the Task

   Determine the percentage of gravel in the final mixture.

   Step 3: Approach Strategically

   Calculate the total weight of gravel and the total weight of the complete mixture. Then divide the weight of gravel by that total weight and convert to a percentage. Batch A, which weighs 1,000 kilograms (kg), contains 30% gravel, so that is 1,000 × 0.30 = 300 kg. Batch B contains 2,000 × 0.40 = 800 kg of gravel. The weight of the gravel in batch C is 1,500 × 0.50 = 750 kg, and the weight of the gravel in batch D is 500 × 0.60 = 300 kg.

   The total weight of gravel is 300 + 800 + 750 + 300 = 2,150 kg, and the weight of the complete mixture is 1,000 + 2,000 + 1,500 + 500 = 5,000 kg. Therefore, the percentage of gravel is . One efficient way to do the division in your head is to think of 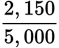 as being equal to . Then convert each of these fractions to 0.40 and 0.03, respectively, and add to get 0.43. (B) is correct.

   Step 4: Confirm Your Answer

   Be certain that you calculated a weighted average; the unweighted simple average is (C) 45%. If you were pressed for time, you could have made an educated guess. By noting that the two largest batches contained 40% and 50% gravel, you could have logically narrowed the choices down to (B) and (C).

8. (C)

   Step 1: Analyze the Question

   This question stem contains information about two periods of sales, one as a percent of a total and the other as a fraction of the remaining total. You are asked to calculate the percent decrease in sales from one quarter to the next. To determine this value, you need the number of crafts sold in each quarter.

   Step 2: State the Task

   Translate the question stem into three equations to determine (1) number of crafts sold in the first quarter, (2) number of crafts sold in the second quarter, and (3) percent decrease in the number of crafts sold.

   Step 3: Approach Strategically

   Translating the first sentence (first quarter), you have 36% × 75 crafts = 0.36 × 75. This arithmetic looks time-consuming. However, 0.75 × 36 produces the same result, and 0.75 is equal to three-fourths. So there were  crafts sold.

   Next, she sold one-fourth of the remaining crafts. The number of crafts remaining is 75 − 27 = 48. Therefore, she sold . 

   The percent change formula is this:

   

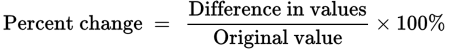
   Plug in the values:

   

   (C) is correct.

   Step 4: Confirm Your Answer

   Make sure you translated each part of the scenario correctly, especially the sentence about the second quarter sales, which describes one-fourth of the remaining crafts. Then double-check your work, especially in setting up the percent change calculation.

9. (C)

   Step 1: Analyze the Question Stem

   This is a Value question. When presented with a chart, take a quick look at the information in it and consider the types of calculations that can be made using that information. This circle graph displays the results of the student survey. Since there are 120 students, the number of students who prefer the science museum is 120 × 0.60, the number of students who prefer the art museum is 120 × 0.30, and the number of students who prefer neither museum is 120 × 0.10.

   The question stem asks how many students will not be able to visit their preferred museum. This question implies that there is some limitation on the number of students who can attend each museum. You can ignore the students who have no preference as they are irrelevant to this question.

   Step 2: Evaluate the Statements Using 12TEN

   Statement (1) indicates that no more than 55 students can visit the science museum for the field trip. Comparing 55 to the number of students who prefer the science museum would allow determination of how many of these students won’t get their first choice. (If you’re curious, 120 × 0.60 = 72 students would like to go, so 72 − 55 = 17 students who don’t get their first choice.) However, this statement alone provides no information about how many students who want to visit the art museum will be denied the opportunity to attend that museum. Eliminate (A) and (D). 

   Statement (2) says that the limitation for the art museum is 50. Again, comparing 50 to the number of students who wish to visit the art museum would allow determination of the number thwarted in their desire. (The number who prefer the art museum is 120 × 0.30 = 36, so all these students get their first choice and the number denied is 0.) By itself, however, this statement provides no information about the students who want to visit the science museum, so eliminate (B). 

   Together, the statements allow calculation of the number of students from the science museum group and the art museum group who will not get their preferred museum. All students who have expressed a preference are accounted for. Thus, (C) is correct.

Practice Set: Mixtures on the GMAT

10. (C)

    Step 1: Analyze the Question Stem

    For this Value question, your first step is to translate the words into math. Let c equal the number of chocolate donuts, j equal the number of jelly donuts, and p equal the number of plain donuts. If T is the total number of donuts, then c + j + p = T and . You want to know how many more chocolate donuts (x) need to be added to make the case consist of one-quarter chocolate donuts. When x chocolate donuts are added, this also adds to the total number of donuts, so  . Substituting   for c makes the equation 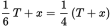. Thus, if you had enough information to determine how many donuts are in the case (T), you could solve for x.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1): While this tells you the number of plain donuts in the case, the fact that p = 40 doesn’t tell you how many donuts there are in total. Thus, Statement (1) is insufficient. Eliminate (A) and (D).

    Now evaluate Statement (2), which provides a ratio between plain donuts and jelly-filled donuts. This tells you how the   of donuts that aren’t chocolate are divvied up between plain and jelly, but since there is no actual number of any of the donut types, this statement does not allow calculation of T or c. Statement (2) is not sufficient. Eliminate (B).

    Now combining the statements, you can say that p = 40 and that , so you can set up a proportion to determine how many jelly-filled donuts there are: 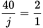 , so 40 = 2j and j = 20. Thus, there are 40 + 20 = 60 non-chocolate donuts in the case. You know that 60 = 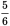  of the total donuts (because 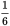  of the donuts are chocolate), so 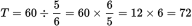  . You’ve determined that finding this is enough to answer the question, so the statements together are sufficient, and the correct choice is (C).

    While you only need to know that you have sufficient information to find a value to answer a Data Sufficiency value question, if you’re curious, here’s what the math would look like.  You’re starting with 72 total donuts, so T = 72:  

    

    

    

    

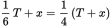
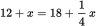
    x = 8

    So you start with 72 total donuts, 12 of which are chocolate. Adding 8 chocolate donuts yields 20 chocolate donuts and 80 total donuts, and the number of chocolate donuts is now 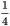 of the total.

11. (B)

    Step 1: Analyze the Question

    The question describes that a particular farmer always has the same total target output for crops each year, growing only corn and soybeans. This year, 24 tons of corn makes up 40% of the output; next year, she wants to grow the same total output but have only 15% be corn. Since the total output remains the same, she is going to grow less corn and more soybeans.

    Step 2: State the Task

    Translate the information into equations to determine how many more tons of soybeans the farmer must grow to reach the desired output level.

    Step 3: Approach Strategically

    First, use the fact that 24 tons of corn makes up 40% of the target output to find the target output amount t: 

    

    

    

    

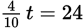
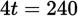
    The total output is 60 tons. Next year, corn will only be 15% of the total output, so that will be 0.15 × 60. You can do this arithmetic quickly in your head: 10% of 60 is 6, and 5% of 60 is half that, or 3. Then (10% + 5%) of 60 is 6 + 3, or 9 tons. This is 15 fewer tons than for the current year. Therefore, to maintain the target output, the farmer will need to grow 15 more tons of soybeans.

    Step 4: Confirm Your Answer

    Make sure you’ve answered the right question. (A) represents the amount of corn the farmer will grow next year, (D) represents the total amount of soybeans grown this year, and (E) represents the total amount of soybeans to be grown next year.

12. (E)

    Step 1: Analyze the Question

    The question provides the relative amounts of solutions containing different stated concentrations of a chemical. These different solutions are combined. The ratio of the solutions is 1:2:4. No actual amounts of solution are given, but since the answer choices are percents, not amounts, you don’t need amounts to solve.

    Step 2: State the Task

    Determine the concentration of Chemical A in the total solution. 

    Step 3: Approach Strategically

    You can determine the final concentration by first calculating the total relative amounts of Chemical A and of the combined solution and then dividing the amount of Chemical A by the total amount of solution. 

    One unit of the 10% solution contains 1 × 0.1 =  0.1 units of Chemical A; 2 units of the 30% solution contain 2 × 0.3 = 0.6 units; 4 units of the 35% solution contain 4 × 0.35 = 1.4 units. So the total amount of Chemical A is 0.1 + 0.6 + 1.4 = 2.1 units. The total volume of the combined solution is 1 + 2 + 4 = 7 units. Thus, the resulting concentration is 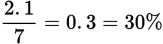. (E) is correct.

    Step 4: Confirm Your Answer

    You can check your result of 30% using the balance approach. One unit of the 10% solution is 1(30 − 10) = 20 below the overall 30%. The 30% solution is the same as the overall concentration, and 4 units of the 35% solution are 4(35 − 30) = 20 above the overall 30%. Thus, the concentrations are “in balance” when the average of 30% is used.