Answers and Explanations

Practice Set: Median, Mode, Range, and Standard Deviation on the GMAT

  1. (A)
    Step 1: Analyze the Question Stem

    This Value question lists the elements of a data set, including the variable x, and asks for the value of that variable.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1): Since the mean of a group of numbers is , you could write the equation  and solve for x. This statement is sufficient, so eliminate (B), (C), and (E).

    Statement (2): In order to determine the median of a list of numbers, restate them in ascending numerical order. Begin by listing the known values: {−5, −1, 0, 1, 2, 9}. Since there are seven values, the fourth greatest value will be the median. Pick some values for x. If x = 1, then the median is 1; thus, x could be 1. However, if x is any value greater than 1, such as 2, then 1 is still the median. Thus, x could be any value equal to or greater than 1. This statement is insufficient, so (A) is correct.

  2. (D)
    Step 1: Analyze the Question

    By saying that the range of these eight numbers is 25, this question is saying that the difference between the largest and smallest value is 25. The range of the seven known numbers in the set is 28 − 4 = 24. Thus, n must be either the largest number or the smallest number in the set.

    Step 2: State the Task

    Determine how far n can be from the smallest known value and the largest known value in the set and then find the difference between those distances.

    Step 3: Approach Strategically

    List the known numbers in order, leaving spaces to visualize where n might be in the list:  _,  4,  8,  9, 11, 14, 17, 28,  _ . The largest known value is 28, so if that were the largest value of all eight numbers, n would have to be 28 − 25 = 3. On the other hand, the smallest known value is 4, so if that were the smallest value, n would have to be 4 + 25 = 29. Thus, n could either be 3 or 29. Therefore, the difference between the largest and smallest possible values of n is 29 − 3 = 26. The correct answer is (D).

    Step 4: Confirm Your Answer

    Review the order of numbers on your list and confirm your calculations. Finally, make sure you answered the question asked, which is not about a possible value of n—(B) and (E) represent n’s possible values—but the difference between its possible values.

  3. (D)

    Step 1: Analyze the Question Stem

    This Value question presents three variables, a, b, and c, and tells you that a is the average of the three values. Also, b and c sum to 0. This means that b and c have the same magnitude (e.g., if b = 2, then c = –2; if b = 0, then c = 0).

    Since b and c are balanced around 0 (their absolute values are equal), a must be exactly between b and c and thus equal to 0. Standard deviation is calculated by finding each number’s distance from the mean as a first step. So for you to be able to determine the standard deviation of a, b, and c, a statement would need to provide either the specific value of b or c or the difference between either of those values and a.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) tells you the difference between b and a. Since the difference between b and the average a is 2, the distance between c and the average is 2, and the distance between a and the average is 0. These are the values you’d use to find the standard deviation, making this statement sufficient. Eliminate (B), (C), and (E).

    Statement (2) gives the difference between c and the average a. As with Statement (1), this tells you the difference between c and the mean and allows you to find the difference between b and the mean, and you already know that the mean is 0. Thus, this statement is sufficient, so (D) is correct.

  4. (C)

    Step 1: Analyze the Question Stem

    This is a Value question. You’re asked for the median of numbers in a set that includes two variables. One way to answer this question would be to find the values of both variables. You can also get to one value for the median of a set of five numbers if you can identify which number has two numbers in the set less than or equal to it and two numbers in the set greater than or equal to it. In other words, you can solve if you can find the number that must be in the middle of the set, even if you’re not sure exactly what that number is.

    Step 2: Evaluate the Statements Using 12TEN

    Since Statement (1) is a quadratic equation with one variable, you might be able solve for a single value of y. However, since this would not tell you the value of x, you wouldn’t know what the median was. Eliminate (A) and (D).

    Evaluating Statement (2) and applying knowledge of number properties (specifically that a negative base raised to an odd exponent results in a negative number), there are two potential scenarios:

    1. x = y, making x − y = 0 and 
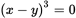
    2. x < y, making x − y < 0 and 

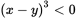
    While Statement (2) provides information on the relationship between the two variables, it does not provide information about the relationship between the variables and the other numbers in the set, which makes it insufficient for the task at hand. Eliminate (B).

    Now try combining the statements. You were able to eliminate Statement (1) without taking the time to solve for y, but it’s now worthwhile to do so:

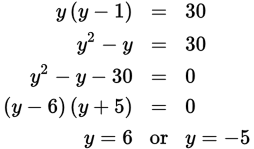
    The question stem indicates that the set only contains even numbers, so you know that y = 6.  

    Based on the other numbers in the set, you know for sure that there are two numbers greater than y (the 18 and the 32). Based on Statement (2), you know that x  is less than or equal to y, which would mean that, in the context of the set, y also has two numbers lesser than or equal to it. The set contains five numbers, so y (which is 6) is the median, and you can definitively answer the question. Because the statements together are sufficient, the correct answer is (C). 

Practice Set: Sequences of Integers on the GMAT

  1. (D)
    Step 1: Analyze the Question

    The question states that the median of a sequence of consecutive integers is 45 and that the sum of all the integers is 1,125. In a sequence of consecutive integers, the median equals the average (arithmetic mean).

    Step 2: State the Task

    Determine the value of the greatest integer in the sequence.

    Step 3: Approach Strategically

    Use the formula for averages to determine how many integers are in the sequence. Then use that information and the given median to find the value of the greatest number in the sequence.

    Rearrange the averages formula to get . So that is . Thus, there will be 1 less than half of 25, or 12, consecutive integers less than 45 and 12 greater than 45. So the greatest value in the sequence is 45 + 12 = 57. (D) is correct.

    Step 4: Confirm Your Answer

    Double-check your calculations to ensure that you haven’t made any avoidable mistakes.

  2. (B)
    Step 1: Analyze the Question

    When working with sets of consecutive numbers, look for ways to save time and work by recognizing patterns and first and last terms in the set.

    To find the sum of terms in a set of consecutive numbers, apply the average formula:

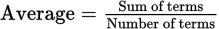
    Sum of terms = (Average)(Number of terms)

    Step 2: State the Task

    To find the sum, you need to calculate the average of the terms in the set and the number of items in the set. 

    Step 3: Approach Strategically

    First, find the smallest and largest multiple of 4 between 13 and 125. In this range, the smallest multiple of 4 is 16, and the largest is 124. Thus, the set of values in this question is really the multiples of 4 from 16 to 124 inclusive.

    The average of a set of consecutive numbers equals the average of the smallest and largest terms. The average of these two numbers is 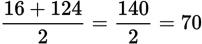. So the average of all terms in this set is 70.

    Now find the number of multiples of 4 between 16 and 124 inclusive. You could simply list all of the terms in the sequence, but that would be time-consuming. A great shortcut to determine this value is to find the difference between the smallest and largest terms and add 1. Because the numbers in this set are multiples of 4, you must divide the difference by 4 before adding 1. Therefore, the number of terms in this set is . 

    So the average of the terms in the set is 70, and the number of terms in the set is 28. The sum of the terms in the set is the product of these two values: 28 × 70 = 1,960. (B) is correct.

    Step 4: Confirm Your Answer

    Pay careful attention to the wording of this question stem. The set is inclusive, so confirm that you added 1 when you calculated the number of terms.

  3. (A)

    Step 1: Analyze the Question Stem

    This is a Yes/No question. If z is the sum of three consecutive odd positive integers, call the smallest integer x and write the other two as (x + 2) and (x + 4), respectively. Therefore, the sum of the three integers is x + (x + 2) + (x + 4) or, combining like terms, 3x + 6. Finally, you can factor to find that the sum is 3(x + 2).

    So the question is really asking, “Is 3(x + 2) evenly divisible by 9?”

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1): You are told that when x is divided by 3, the remainder is 1. So x is 3 times some integer plus 1. Call that integer y and substitute 3y + 1 for x in the expression above to get 3(3y + 1 + 2) = 3(3y + 3). When the factor is distributed, this is 9y + 9.  Since y is an integer, this expression must be divisible by 9. So the answer is always yes, and Statement (1) is sufficient. Eliminate (B), (C), and (E).

    If you prefer picking numbers to algebra, you could set x = 1. If x = 1, then the sum of the 3 numbers is 1 + 3 + 5 = 9. Then you could try x = 7, the next odd number that leaves a remainder of 1 when divided by 3, and get a sum of 27, which is also divisible by 9. Each time you increase x by 6 to find the next odd integer that leaves a remainder of 1 when divided by 3, the sum increases by 18, so the relationship holds true.

    Statement (2): You can check this statement for sufficiency by picking numbers. If x = 7, then the sum is 3(7 + 2) = 27, which is divisible by 9. However, if x = 21, the next odd number divisible by 7, then the sum is 3(21 + 2)= 69, which is not divisible by 9. Therefore, Statement (2) is insufficient. The correct choice is (A).

  4. (C)
    Step 1: Analyze the Question

    There are two sequences of integers. The sum of the sequence with six consecutive integers is Z. The second sequence consists of five consecutive integers, the sum of which is Z − 5. The greatest integer in this latter sequence is 40. 

    Step 2: State the Task

    Determine the difference between the median, or middle, term of the five-number sequence and the smallest term of the six-number sequence.

    Step 3: Approach Strategically

    If the greatest term in the five-number sequence is 40, that sequence must be 36, 37, 38, 39, 40. The sum of a sequence of integers is the average (arithmetic mean) times the number of terms. Since this sequence has an odd number of consecutive terms, the middle or median value, 38, is also the mean. Thus, the sum of terms in this sequence is 38 × 5 = 190. Since this sum is equivalent to Z − 5, Z = 195.

    Since the sum of terms in the six-term sequence is 195, then using the formula   yields 195 ÷ 6 = 32.5. This sequence has an even number of terms, so the mean is the average of the two middle terms when all of the terms are arranged in numeric order. Therefore, the third and fourth terms in the sequence must be 32 and 33, and the entire sequence is 30, 31, 32, 33, 34, 35. Thus, the difference between the third term of the five-number sequence (38) and the smallest term of the six-number sequence (30) is 8, which is (C).

    Step 4: Confirm Your Answer

    Go back over the question stem to make sure that you didn’t misread anything. Then check your determination of the sequences to make sure you selected the correct values to compare.

Practice Set: Combinations and Permutations on the GMAT

  1. (E)
    Step 1: Analyze the Question

    The question describes the creation of an organizational structure and the divisions that could be included in it. Since nothing indicates that order matters (for an organization to have Divisions A and B is exactly like that organization having Divisions B and A), this is a combinations question.

    Step 2: State the Task

    Find the number of organizational structures that can be made according to these specifications, using the combinations formula as needed.

    Step 3: Approach Strategically

    Since Division A must be part of the organization, there is only 1 way to choose that unit.

    If at least one of B and C must be in the organization, only B, only C, or both could be in it, making for 3 possible ways to choose from these divisions.

    At least two of D, E, and F must be part of the organization. If two join, there are 3 possible outcomes: D and E, D and F, or E and F. Or all three could be included, which is 1 more outcome. So there are 4 possible ways to choose this group of units.

    Finally, at least two of G, H, J, and K must be included. If two are included,  possible outcomes. If three of these divisions are used, there are four ways to leave one division out, so that’s 4 possible outcomes. If all four are included, that’s 1 more outcome. Thus, there are 11 possible ways to choose divisions from this group.

    To find the number of organizational structures that can be formed from these various groups, multiply the numbers of ways of selecting each group: 1 × 3 × 4 × 11 = 132. 

    Step 4: Confirm Your Answer

    Make sure you counted all of the possibilities for including the divisions in counting the number of possible organizational structures.

  2. (D)
    Step 1: Analyze the Question

    For any question that asks you to make subsets or groups of a larger pool of items, pay careful attention to the wording of the question stem. You need to determine whether the order of the items in each subgroup matters. In this question, you are asked to make distinct combinations of 3 wires from a set of 5 wires. Because you want distinct combinations, the order of the wires will not matter, and you can apply the combinations formula to solve the question. Notice the phrase “at least” in the question stem. When questions use that phrase, solving for the total and then subtracting the undesired outcomes is usually a very efficient approach. The total is the number of ways one could select any 3 wires from 5. The undesired outcome is selecting only telephone wires.

    Step 2: State the Task

    Apply the combinations formula to determine how many subsets of 3 wires can be created from the pool of 5 wires. Then determine how many ways there are to select only 3 telephone wires and subtract.

    Step 3: Approach Strategically

    Use the combinations formula, , to find the total number of ways to choose 3 wires out of 5. Substituting 5 for n and 3 for k, you find that the total number of ways to choose 3 wires out of 5 is:

    You now know that there are 10 subsets of 3 wires. Now turn your attention to what is undesired—selecting only telephone wires. Because there are only 3 telephone wires, there is only 1 possible way to choose 3 of the 5 wires such that all are telephone wires. Thus, there are 10 − 1 = 9 ways to choose 3 wires such that at least 1 of the wires would be for cable. (D) is correct.

    Step 4: Confirm Your Answer

    Pay careful attention to exactly what the question stem is asking. Notice that (E) is a trap for the unwary test taker who simply calculates the total number of possible outcomes.

  3. (C)

    Step 1: Analyze the Question Stem

    This Value question describes lining up different candles and figurines in such a way that no two of the same type of object are adjacent to each other and asks how many different arrangements can be made. In order to determine that value, you would need to know the exact number of each object.

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1) tells you that 40,320 arrangements can be made using only the distinct figurines. If the number of figurines is f, then the number of arrangements is f! = 40,320. You could solve this for the number of figurines, but there’s no need to do so on Test Day (but for the record, 8! = 40,320). However, you don’t know the number of candles. The row could start and end with a candle, in which case there would be f + 1 candles, there could be equal numbers of candles and figures, or the row could start and end with figurines, meaning that there would be f − 1 candles. Thus, Statement (1) is insufficient. Eliminate (A) and (D).

    Statement (2) informs you that there’s one more candle than figurine, but does not tell you how many there are. This is insufficient, so eliminate (B) and proceed to evaluate the statements together.

    Statement (1) enables you to calculate the number of figurines and Statement (2) tells you that there’s one more candle. So you know the numbers of each object, which is sufficient to determine the number of arrangements. (C) is correct.

  4. (B)
    Step 1: Analyze the Question

    The question states that there are 6 identical chips, each with a red side and a blue side. Since the chips are identical, there is no way to distinguish among any chips with the same color showing.

    Step 2: State the Task

    Determine the difference between the number of ways that 3 red-sided and 3 blue-sided chips can be arranged and the number of ways 4 red-sided and 2 blue-sided chips can be arranged.

    Step 3: Approach Strategically

    If the chips were all different from each other, there would be 6! ways to arrange them. However, that number must be reduced by factors that represent the number of ways that the red sides can be arranged and the blue sides can be arranged, since all of these configurations are identical.

    For 3 of each color, divide 6! by 3! twice to represent the indistinguishable arrangements of 3 blue and 3 red chips. Thus, the number of ways to arrange the chips is  . Similarly, the number of ways to arrange 4 reds and 2 blues is  . Since 20 − 15 = 5, (B) is correct.

    Step 4: Confirm Your Answer

    Check that you answered the question that is actually asked. (C) is merely the number of chips, and (D) and (E) represent the number of arrangements for each of the two configurations.

Practice Set: Probability on the GMAT

  1. (C)
    Step 1: Analyze the Question

    Three bags are randomly chosen, without replacement, from a shed containing 3 kinds of bags. You’re given the total number of bags (8) and the numbers of fertilizer (2) and grass seed (3) bags, so the starting number of non-mulch bags is 2 + 3 = 5.

    Step 2: State the Task

    Use the probability formula for dependent events to find the probability of not choosing a bag of mulch 3 times.

    Step 3: Approach Strategically

    Probability is . There are 8 total bags and 5 of them do not have mulch, so the first time you pick a bag out of the shed, there is a 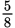chance of getting a non-mulch bag.

    This bag is not replaced, so now there are 7 total bags and 4 are non-mulch: that’s a 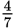 probability.

    One more bag to pick up: this time there are 6 total bags and 3 non-mulch, so there is a 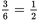 chance of getting the desired result this time.

    To achieve the desired result, you need to get 1 non-mulch bag and a second one and a third one. This means you multiply the individual events’ probabilities: 

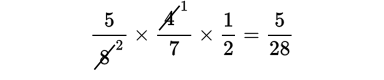
    (C) is correct.

    Step 4: Confirm Your Answer

    Reread the question stem to ensure that you understood the scenario correctly, and double-check that you didn’t make any mistakes in calculating the probabilities.

  2. (C)
    Step 1: Analyze the Question

    The question says that there are 2 different bags containing 9 marbles each. One bag contains 4 red marbles, and the other bag has 3 red marbles. A marble is selected randomly from each of the bags.

    Step 2: State the Task

    Determine the probability that exactly 1 of the 2 marbles that is drawn is red.

    Step 3: Approach Strategically

    There are two ways to select exactly 1 red marble. One way is to select a red marble from the first bag and a non-red marble from the second bag. The other way is to select a non-red marble from the first bag and a red marble from the second bag. Since the desired result can be attained in one manner or another, add these two probabilities to get the total probability of selecting exactly 1 red marble.

    The probability that the red marble is chosen from the first bag is , and the probability that a non-red marble is chosen from the second bag is . Since both of these outcomes must occur, multiply their probabilities to get 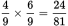 . There is no need to simplify at this point because you will be adding this to another fraction.

    The probability that a non-red marble is chosen from the first bag is  , and the probability that a red marble is chosen from the second bag is  . Since both of these outcomes must occur, multiply their probabilities to get  .

    Now, add the probabilities of the two desired outcomes; the probability that exactly 1 of the chosen marbles is red is  . (C) is correct.

    Step 4: Confirm Your Answer

    Confirm that these two scenarios are the only two ways in which the desired outcome can occur. (A) is the probability that both marbles will be red, and (D) is the probability that one or both will be red.

  3. (E)
    Step 1: Analyze the Question

    The question states that an event has two equally likely outcomes and that they are mutually exclusive. In other words, every time the event happens, there’s a 50% chance of outcome A and a 50% chance of outcome B.

    Step 2: State the Task

    Determine the probability that fewer than half of 5 random trials result in outcome A.

    Step 3: Approach Strategically

    The probability that less than half of 5 trials have an outcome of A is the total of the probability of 0, 1, or 2 outcome As. Use the probability formula  to determine this probability.

    Since each occurrence has 2 possible outcomes, the total number of possible outcomes is 25 = 32. There is only 1 way to have no As, that is, 5 Bs. There are 5 ways to have 1 A, since that singular A could occur on any 1 of the 5 trials.

    There are 2 ways to find the number of ways to get 2 As. You could actually count the ways: AABBB, ABABB, ABBAB, ABBBA, BAABB, BABAB, BABBA, BBAAB, BBABA, and BBBAA, for a total of 10 different ways. Alternatively, you could use the combinations formula to find the number of combinations of 2 As out of 5 events:  

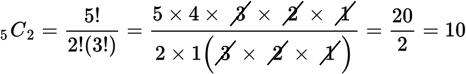
    The total number of ways to obtain the desired outcome is thus 1 + 5 + 10 = 16, so the probability is . (E) is correct.

    Step 4: Confirm Your Answer

    Be certain that you answered the question that was asked and counted all the ways to get 2 or less outcomes of A. Although it may seem counterintuitive that the probability of getting less than half As is exactly , you can verify that this is correct by checking to see if the probability of all outcomes is equal to 1. The same calculations would show that the probability for 0, 1, or 2 Bs, is also . Since this corresponds to 3, 4, or 5 As, the total probability of 0, 1, 2, 3, 4, or 5 As is  . Put another way, since there are 6 different numbers of As that are possible (from 0 to 5), getting 0, 1, or 2 As does in fact cover half the possibilities. 

  4. (D)

    Step 1: Analyze the Question Stem

    This Value question asks for the probability that a student receives housing in at least one of two consecutive years. In order to calculate that probability, you would need to know the probability of getting housing in each year. (Another possibility that could be useful is the chance of not getting housing, since 1 − Undesired Probability = Desired Probability.)

    Step 2: Evaluate the Statements Using 12TEN

    Statement (1): This gives you the probability of not getting into housing. An 80% chance of not getting housing each year means a 20% chance of getting housing each year. The exact answer isn’t something that you need to worry about, since this isn’t Problem Solving. You know an answer can be calculated, so Statement (1) is sufficient. Eliminate choices (B), (C), and (E).

    Statement (2): This isn’t given in percentage form, but any proportion will serve. This gives you the likelihood of getting housing in any given year. You now know that Statement (2), which gives you the same information that Statement (1) does, must be sufficient. (D) is correct.