Figure 1.1 The Cyrillic alphabet used for Russian
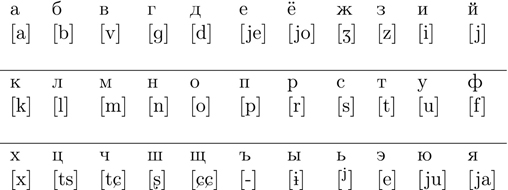
One of the aims of this book is to introduce you to different ways that computers are able to process natural language. To appreciate this task, consider how difficult it is to describe what happens when we use language. As but one example, think about what happens when a friend points at a book and says: “He’s no Shakespeare!”. First of all, there is the difficulty of determining who is meant by “he”. Your friend is pointing at a book, not at a person, and although we can figure out that “he” most likely refers to the author of the book, this is not obvious to a computer (and sometimes not obvious to the person you are talking with). Secondly, there is the difficulty of knowing who “Shakespeare” is. Shakespeare is the most famous writer in the English language, but how does a computer know that? Or, what if your friend had said “He’s no Lessing!”? English majors with an interest in science-fiction or progressive politics might take this as a reference to Doris Lessing; students of German literature might suspect a comparison to G.E. Lessing, the elegant Enlightenment stylist of German theater; but in the absence of background knowledge, it is hard to know what to make of this remark.
Finally, even if we unpack everything else, consider what your friend’s statement literally means: the author of this book is not William Shakespeare. Unless there is a serious possibility that the book was written by Shakespeare, this literal meaning is such a crushingly obvious truth that it is difficult to see why anyone would bother to express it. In context, however, we can tell that your friend is not intending to express the literal meaning, but rather to provide a negative evaluation of the author relative to Shakespeare, who is the standard benchmark for good writing in English. You could do the same thing for a slim book of mystical poetry by saying “She’s no Dickinson!”, provided the hearer was going to understand that the reference was to American poet Emily Dickinson.
Or consider a different kind of statement: “I’m going to the bank with a fishing pole.” Most likely, this means that the speaker is going to a river bank and is carrying a fishing pole. But it could also mean that the speaker is going to a financial institution, carrying a fishing pole, or it could mean that the speaker is going to a financial institution known for its fishing pole – or even that the river bank the speaker is going to has some sort of notable fishing pole on it. We reason out a preferred meaning based on what we know about the world, but a computer does not know much about the world. How, then, can it process natural language?
From the other side of things, let us think for a moment about what you may have observed a computer doing with natural language. When you get a spam message, your email client often is intelligent enough to mark it as spam. Search for a page in a foreign language on the internet, and you can get an automatic translation, which usually does a decent job informing you as to what the site is about. Your grammar checker, although not unproblematic, is correct a surprising amount of the time. Look at a book’s listing on a site that sells books, like Amazon, and you may find automatically generated lists of keywords; amazingly, many of these words and phrases seem to give a good indication of what the book is about.
If language is so difficult, how is it that a computer can “understand” what spam is, or how could it possibly translate between two languages, for example from Chinese to English? A computer does not have understanding, at least in the sense that humans do, so we have to wonder what technology underlies these applications. It is these very issues that we delve into in this book.
There is a fundamental issue that must be addressed here before we can move on to talking about various applications. When a computer looks at language, what is it looking at? Is it simply a variety of strokes on a piece of paper, or something else? If we want to do anything with language, we need a way to represent it.
This chapter outlines the ways in which language is represented on a computer; that is, how language is encoded. It thus provides a starting point for understanding the material in the rest of the chapters.
If we think about language, there are two main ways in which we communicate – and this is true of our interactions with a computer, too. We can interact with the computer by writing or reading text or by speaking or listening to speech. In this chapter, we focus on the representations for text and speech, while throughout the rest of the book we focus mainly on processing text.
If we only wanted to represent the 26 letters of the English alphabet, our task would be fairly straightforward. But we want to be able to represent any language in any writing system, where a writing system is “a system of more or less permanent marks used to represent an utterance in such a way that it can be recovered more or less exactly without the intervention of the utterer” (Daniels and Bright, 1996).
And those permanent marks can vary quite a bit in what they represent. We will look at a basic classification of writing systems into three types: alphabetic, syllabic, and logographic systems. There are other ways to categorize the world’s writing systems, but this classification is useful in that it will allow us to look at how writing systems represent different types of properties of a language by means of a set of characters. Seeing these differences should illustrate how distinct a language is from its written representation and how the written representation is then distinct from the computer’s internal representation (see Section 1.3).
For writing English, the idea is that each letter should correspond to an individual sound, more or less, but this need not be so (and it is not entirely true in English). Each character could correspond to a series of sounds (e.g., a single character for str), but we could also go in a different direction and have characters refer to meanings. Thus, we could have a character that stands for the meaning of “dog”. Types of writing systems vary in how many sounds a character represents or to what extent a meaning is captured by a character. Furthermore, writing systems differ in whether they even indicate what a word is, as English mostly does by including spaces; we will return to this issue of distinguishing words in Section 3.4.
One important point to remember is that these are systems for writing down a language; they are not the language itself. The same writing system can be used for different languages, and the same language in principle could be written down in different writing systems (as is the case with Japanese, for example).
We start our tour of writing systems with what should be familiar to any reader of English: alphabets. In alphabetic systems, a single character refers to a single sound. As any English reader knows, this is not entirely true, but it gives a good working definition.
We will look at two types of alphabetic systems. First, there are the alphabets, or phonemic alphabets, which represent all sounds with their characters; that is, both consonants and vowels are represented. Many common writing systems are alphabets: Etruscan, Latin, Cyrillic, Runic, and so forth. Note that English is standardly written in the Latin, or Roman, alphabet, although we do not use the entire repertoire of available characters, such as those with accents (e.g., è) or ligatures, combinations of two or more characters, such as the German ß, which was formed from two previous versions of s.
As an example of an alphabet other than Latin, we can look at Cyrillic, shown in Figure 1.1. This version of the alphabet is used to write Russian, and slight variants are used for other languages (e.g., Serbo-Croatian). Although some characters correspond well to English letters, others do not (e.g., the letter for [n]). The characters within brackets specify how each letter is said – that is, pronounced; we will return to these in the discussion of phonetic alphabets later on.
Figure 1.1 The Cyrillic alphabet used for Russian
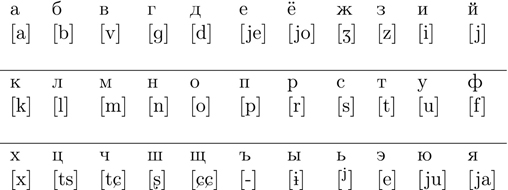
Some alphabets, such as the Fraser alphabet used for the Lisu language spoken in Myanmar, China, and India, also include diacritics to indicate properties such as a word’s tone (how high or low pitched a sound is). A diacritic is added to a regular character, for example a vowel, indicating in more detail how that sound is supposed to be realized. In the case of Fraser, for example, M: refers to an [m] sound (written as M), which has a low tone (written as :).
Our second type of alphabetic system also often employs diacritics. Abjads, or consonant alphabets, represent consonants only; some prime examples are Arabic, Aramaic, and Hebrew. In abjads, vowels generally need to be deduced from context, as is illustrated by the Hebrew word for “computer”, shown on the left-hand side of Figure 1.2.
Figure 1.2 Example of Hebrew (abjad) text
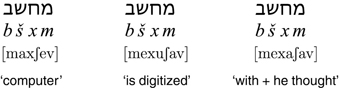
The Hebrew word in its character-by-character transliteration bšxm contains no vowels, but context may indicate the [a] and [e] sounds shown in the pronunciation of the word [max∫ev]. (Note that Hebrew is written right to left, so the m as the rightmost character of the written word is the first letter pronounced.) As shown in the middle and right-hand side of Figure 1.2, the context could also indicate different pronunciations with different meanings.
The situation with abjads often is a little more complicated than the one we just described, in that characters sometimes represent selected vowels, and often vowel diacritics are available.
As we have discussed, alphabets use letters to encode sounds. However, there is not always a simple correspondence between a word’s spelling and its pronunciation. To see this, we need look no further than English.
English has a variety of non-letter–sound correspondences, which you probably labored through in first grade. First of all, there are words with the same spellings representing different sounds. The string ough, for instance, can be pronounced at least five different ways: “cough”, “tough”, “through”, “though”, and “hiccough”. Letters are not consistently pronounced, and, in fact, sometimes they are not pronounced at all; this is the phenomenon of silent letters. We can readily see these in “knee”, “debt”, “psychology”, and “mortgage”, among others. There are historical reasons for these silent letters, which were by and large pronounced at one time, but the effect is that we now have letters we do not speak.
Aside from inconsistencies of pronunciation, another barrier to the letter–sound correspondence is that English has certain conventions where one letter and one sound do not cleanly map to one another. In this case, the mapping is consistent across words; it just uses more or less letters to represent sounds. Single letters can represent multiple sounds, such as the x in “tax”, which corresponds to a k sound followed by an s sound. And multiple letters can consistently be used to represent one sound, as in the th in “the” or the ti in “revolution”.
Finally, we can alternate spellings for the same word, such as “doughnut” and “donut”, and homophones show us different words that are spelled differently but spoken the same, such as “colonel” and “kernel”.
Of course, English is not the only language with quirks in the letter–sound correspondences in its writing system. Looking at the examples in Figure 1.3 for Irish, we can easily see that each letter does not have an exact correspondent in the pronunciation.
Figure 1.3 Some Irish expressions

The issue we are dealing with here is that of ambiguity in natural language, in this case a letter potentially representing multiple possible sounds. Ambiguity is a recurring issue in dealing with human language that you will see throughout this book. For example, words can have multiple meanings (see Chapter 2); search queries can have different, often unintended meanings (see Chapter 4); and questions take on different interpretations in different contexts (see Chapter 6). In this case, writing systems can be designed that are unambiguous; phonetic alphabets, described next, have precisely this property.
You have hopefully noticed the notation used within the brackets ([]). The characters used there are a part of the International Phonetic Alphabet (IPA). Several special alphabets for representing sounds have been developed, and probably the best known among linguists is the IPA. We have been discussing problems with letter–sound correspondences, and phonetic alphabets help us discuss these problems, as they allow for a way to represent all languages unambiguously using the same alphabet.
Each phonetic symbol in a phonetic alphabet is unambiguous: the alphabet is designed so that each speech sound (from any language) has its own symbol. This eliminates the need for multiple symbols being used to represent simple sounds and one symbol being used for multiple sounds. The problem for English is that the Latin alphabet, as we use it, only has 26 letters, but English has more sounds than that. So, it is no surprise that we find multiple letters like th or sh being used for individual sounds.
The IPA, like most phonetic alphabets, is organized according to the articulatory properties of each sound, an issue to which we return in Section 1.4.2. As an example of the IPA in use, we list some words in Figure 1.4 that illustrate the different vowels in English.
Figure 1.4 Example words for English vowels (varies by dialect)
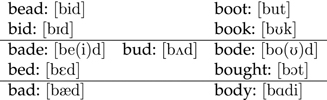
At http://purl.org/lang-and-comp/ipa you can view an interactive IPA chart, provided by the University of Victoria’s Department of Linguistics. Most of the English consonants are easy to figure out, e.g., [b] in “boy”, but some are not obvious. For example, [θ] stands for the th in “thigh”; [ð] for the th in “thy”; and [∫] for the sh in “shy”.
syllabic system are like alphabetic systems in that they involve a mapping between characters and sounds, but the units of sound are larger. The unit in question is called the syllable. All human languages have syllables as basic building blocks of speech, but the rules for forming syllables differ from language to language. For example, in Japanese a syllable consists of a single vowel, optionally preceded by at most one consonant, and optionally followed by [m], [n], or [ŋ]. Most of the world’s languages, like Japanese, have relatively simple syllables. This means that the total number of possible syllables in the language is quite small, and that syllabic writing systems work well. But in English, the vowel can also be preceded by a sequence of several consonants (a so-called consonant cluster), and there can also be a consonant cluster after the vowel. This greatly expands the number of possible syllables. You could design a syllabic writing system for English, but it would be unwieldy and difficult to learn, because there are so many different possible syllables.
There are two main variants of syllabic systems, the first being abugidas (or alphasyllabaries). In these writing systems, the symbols are organized into families. All the members of a family represent the same consonant, but they correspond to different vowels. The members of a family also look similar, but have extra components that are added in order to represent the different vowels. What is distinctive about an abugida is that this process is systematic, with more or less the same vowel components being used in each family.
To write a syllable consisting of a consonant and a vowel, you go to the family for the relevant consonant, then select the family member corresponding to the vowel that you want. This works best for languages in which almost all syllables consist of exactly one consonant and exactly one vowel. Of course, since writing is a powerful technology, this has not stopped abugidas from being used, with modifications, to represent languages that do not fall into this pattern. One of the earliest abugidas was the Brahmi script, which was in wide use in the third century BCE and which forms the basis of many writing systems used on the Indian subcontinent and its vicinity.
As an example, let us look at the writing system for Burmese (or Myanmar), a Sino-Tibetan language spoken in Burma (or Myanmar). In Figure 1.5, we see a table displaying the base syllables.
Figure 1.5 Base syllables of the Burmese abugida
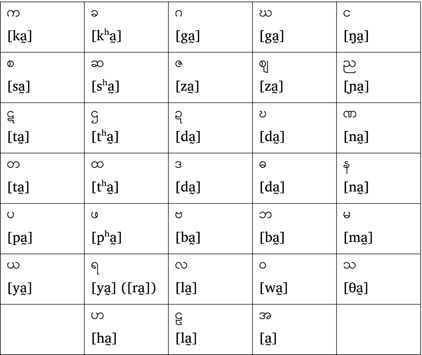
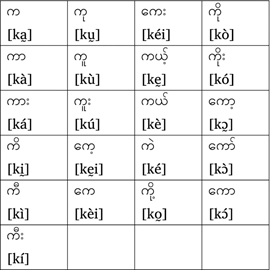
As you can see in the table, every syllable has a default vowel of. This default vowel can be changed by adding diacritics, as shown in Figure 1.6, for a syllables that start with [k]. We can see that the base character remains the same in all cases, while diacritics indicate the vowel change. Even though there is some regularity, the combination of the base character plus a diacritic results in a single character, which distinguishes abugidas from the alphabets in Section 1.2.1. Characters are written from left to right in Burmese, but the diacritics appear on any side of the base character.
Figure 1.6 Vowel diacritics of the Burmese abugida
The second kind of syllabic system is the syllabary. These systems use distinct symbols for each syllable of a language. An example syllabary for Vai, a Niger-Congo language spoken in Liberia, is given in Figure 1.7 (http://commons.wikimedia.org/wiki/Category:Vai-script).
An abugida is a kind of syllabary, but what is distinctive about a general syllabary is that the syllables need not be organized in any systematic way. For example, in Vai, it is hard to see a connection between the symbols for [pi] and [pa], or any connection between the symbols for [pi] and [di].
The final kind of writing system to examine involves logographs, or logograms. A logograph is a symbol that represents a unit of meaning, as opposed to a unit of sound. It is hard to speak of a true logographic writing system because, as we will see, a language like Chinese that uses logographs often also includes phonetic information in the writing system.
To start, we can consider some non-linguistic symbols that you may have encountered before. Figure 1.8, for example, shows symbols found on US National Park Service signs (http://commons.wikimedia.org/wiki/File:National-Park-Service-sample-pictographs.svg). These are referred to as pictographs, or pictograms, because they essentially are pictures of the items to which they refer. In some sense, this is the simplest way of encoding semantic meaning in a symbol. The upper left symbol, for instance, refers to camping by means of displaying a tent.
Some modern systems evolved from a more pictographic representation into a more abstract symbol. To see an example of such character change, we can look at the development of the Chinese character for “horse”, as in Figure 1.9 (http://commons.wikimedia.org/wiki/Category:Ancient-Chinese-characters).
Figure 1.7 The Vai syllabary

Originally, the character very much resembled a horse, but after evolving over the centuries, the character we see now only bears a faint resemblance to anything horse-like.
Figure 1.8 US National Park Service symbols (pictographs)

Figure 1.9 The Chinese character for “horse”

Figure 1.10 Semantic–Phonetic Compounds used in writing Chinese

There are characters in Chinese that prevent us from calling the writing system a fully meaning-based system. Semantic-phonetic compounds are symbols with a meaning element and a phonetic element. An example is given in Figure 1.10, where we can see that, although both words are pronounced the same, they have different meanings depending on the semantic component. Of course, it is not a simple matter of adding the phonetic and semantic components together: knowing that the meaning component of a semantic-phonetic compound is “wood” by itself does not tell you that the meaning of the compound is “timber”.
In addition to writing systems making use of characters differentiated by the shape and size of different marks, there are other writing systems in existence that exploit different sensory characteristics.
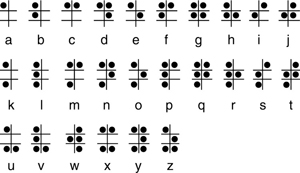
Perhaps best known is the tactile system of Braille. Braille is a writing system that makes it possible to read and write through touch, and as such it is primarily used by the blind or partially blind.We can see the basic alphabet in Figure 1.11 (http://commons.wikimedia.org/wiki/File:Braille-alfabet.jpg). The Braille system works by using patterns of raised dots arranged in cells of up to six dots, in a 3 x 2 configuration. Each pattern represents a character, but some frequent words and letter combinations have their own pattern. For instance, the pattern for f also indicates the number 6 and the word “from”. So, even though it is at core an alphabet, it has some logographic properties.
Figure 1.11 The Braille alphabet
An interesting case is the chromatographic writing system supposedly used by the Benin and Edo people in southern Nigeria (http://purl.org/lang-and-comp/chroma). This system is based on different color combinations and symbols. We have some reservations in mentioning this system, as details are difficult to obtain, but in principle both color and shape can encode pronunciation.
As we mentioned before, there is no simple correspondence between a writing system and a language. We will look at two examples, Korean and Azeri, which will highlight different aspects of the unique ways languages are written.
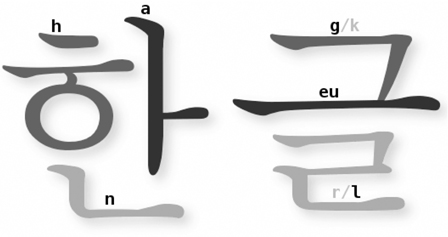
The writing system for Korean is a hybrid system, employing both alphabetic and syllabic concepts. The writing system is actually referred to as Hangul (or Hangeul) and was developed in 1444 during the reign of King Sejong. The Hangul system contains 24 letter characters, 14 consonants and 10 vowels. But when the language is written down, the letters are grouped together into syllables to form new characters. The letters in a syllable are not written separately as in the English system, but together form a single character. We can see an example in Figure 1.12 (http://commons.wikimedia.org/wiki/File:Hangeul.png), which shows how individual alphabetic characters together form the syllabic characters for “han” and “geul”. The letters are not in a strictly left-to-right or top-to-bottom pattern, but together form a unique syllabic character. Additionally, in South Korea, hanja (logographic Chinese characters) are also used.
Figure 1.12 Composition of the characters for “Hangeul”
Azeri is a language whose history illustrates the distinction between a language and its written encoding. Azeri is spoken in Azerbaijan, northwest Iran, and Georgia, and up until the 1920s it was written in different Arabic scripts. In 1929, however, speakers were forced to switch to the Latin alphabet for political reasons. In 1939, it was decided to change to the Cyrillic alphabet, to bring Azeri more in line with the rest of the Soviet Union. After the fall of the USSR in 1991, speakers went back to the Latin alphabet, although with some minor differences from when they had used it before. Azeri is thus a single language that has been written in many ways.
Given the range of writing systems, we now turn to the question of how to encode them on a computer. But to address that, we have a more fundamental question: How do we encode anything on a computer?
To answer that, we need to know that information on a computer is stored in bits. We can think of the memory of a computer as, at its core, a large number of on–off switches. A bit has two possible values, 1 (yes) or 0 (no), allowing us to flip the switches on or off. A single bit on its own does not convey much information, but multiple bits can come together to make meaningful patterns. It is thus often more convenient to speak of a byte, or a sequence of 8 bits, e.g., 01001010.
These sequences of bits tell the computer which switches are on and which are off, and – in the context of writing systems – a particular character will have a unique pattern of on–off switches. Before we fully spell that out, though, let us consider a better way to think of sequences of bits, other than just a sequence of mindless 0s and 1s.
Bit sequences are useful because they can represent numbers, in so-called binary notation. They are called binary because there are only two digits to work with. The base ten numbers we normally use have columns for ones, tens, hundreds, and so on; likewise, binary numbers have their own columns, for ones, twos, fours, eights, and so on. In addition to base two and base ten, there are encodings such as hexadecimal, where there are 16 digits (0–9 and then the letters A–F).
In Big Endian notation, the most significant bit is the leftmost one; this is the standard way of encoding and is parallel to decimal (base ten) numbers. The positions in a byte thus encode the top row of Figure 1.13. As we can see in the second row of the figure, the positions for 64, 8, and 2 are “on”, and 64 + 8 + 2 equals 74. The binary (base two) number 01001010 therefore corresponds to the decimal number 74.
Figure 1.13 Example of Big Endian notation for binary numbers
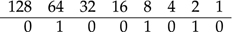
Little Endian notation is just the opposite, where the most significant bit is the rightmost one, but it is less common. In both cases, the columns are all powers of two. This is just like with decimal numbers, where the columns are all powers of ten. As each digit is here limited to either 0 or 1 (two choices), we have to use powers of two.
Although many of you are likely already familiar with binary numbers, it is instructive to see how to convert from decimal to binary notation. We will consider the division method of conversion and walk through an example, converting the decimal number 9 into a 4-bit binary number.
The division method is easy to calculate and moves from the least significant to the most significant bit. Because every column has a value that is a multiple of 2, we divide by 2 with every step. In Figure 1.14, for example, we divide 9 by 2 and find that we have a remainder. A remainder after dividing by 2 means that we started with an odd number. Since 9 is odd, the rightmost bit should be 1.
Figure 1.14 The division method

The trick now is to take the resulting value, in this case 4, and divide it by 2. The same principle is at work here: if there is no remainder, it means that the starting number (4) was even, and this bit needs to be switched off for that to happen.
With 8 bits (a single byte) and each byte storing a separate character, we can represent 256 different characters (= 28). This is sufficient for many applications and more than enough for anyone wishing simply to type in Latin characters for English. With 256 possible characters, we can store every single letter used in English, plus all the auxiliary characters such as the comma, the space, the percent sign, and so on.
One of the first encodings for storing English text used only 7 bits, thus allowing for 128 possible characters. This is the ASCII encoding, the American Standard Code for Information Interchange. We can see most of the ASCII chart in Figure 1.15.
Figure 1.15 The ASCII chart
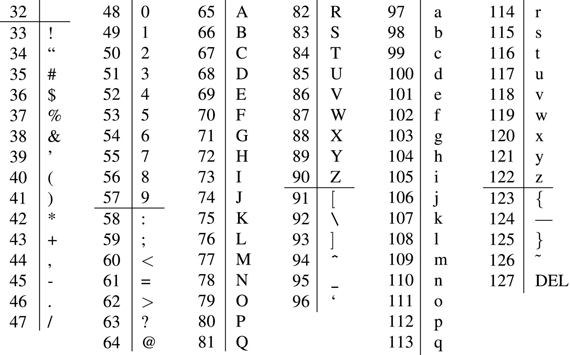
Omitted from the chart are codes 1–31, since these are used for control characters, such as a backspace, line feed, or tab. A nice property is that the numeric order reflects alphabetic ordering (e.g., 65 through 90 for uppercase letters). Thus, we can easily alphabetize the letters by comparing numbers. Although we have written the base ten number, for ease of reading, the binary number is what is used internally by the computer.
You might already be familiar with ASCII or other character-encoding systems, as many communications over email and the internet inform you of different encodings. Emails come with lots of information about themselves. Specifically, Multipurpose Internet Mail Extensions (MIME) provide meta-information on the text, or information that is part of the regular message, but also tell us something about that message. MIME information tells us, among other things, what the character set is; an example can be seen in Figure 1.16.
Figure 1.16 MIME example

We have just mentioned ASCII and that there are other encoding systems, and, as you may recall, one of our goals is to be able to encode any language. With only 128 possible characters, ASCII clearly is insufficient for encoding the world’s writing systems. How, then, do we go about encoding writing systems other than the Latin alphabet?
One approach is simply to extend the ASCII system with various other systems. For example, ISO-8859-1 is an 8-bit encoding that in addition to ASCII includes extra letters needed for French, German, Spanish, and related languages; ISO-8859-7 is for the Greek alphabet; ISO-8859-8 for the Hebrew alphabet; and JIS-X-0208 encodes Japanese characters. While multiple encoding systems make it possible to specify only the writing systems one wants to use, there are potential problems. First, there is always the possibility of misidentification. Two different encodings can use the same number for two different characters or, conversely, different numbers for the same character. If an encoding is not clearly identified and needs to be guessed, for example by a web browser displaying a web page that does not specify the encoding explicitly, the wrong characters will be displayed. Secondly, it is a hassle to install and maintain many different systems in order to deal with various languages.
Unicode (http://www.unicode.org) is a system that addresses these problems by having a single representation for every character in any existing writing system. While based on the earlier discussion we have some idea about the variety of writing systems, we may not have a good feel for how many characters there are to encode in the world. Unicode, version 6.0, has codes for over 109,000 characters from alphabets, syllabaries, and logographic systems. While this sounds like a lot, it should be noted that Unicode uses 32 bits to encode characters. The number of distinct characters a system can encode is equal to 2n, where n is the number of bits: with 7 bits, we had 27 (=128) possibilities. With 32 bits, we can store 232 = 4, 294, 967, 296 unique characters.
At this point, we should consider the situation: Unicode allows for over four billion characters, yet only needs about 100,000. If we use 32 bits to encode every character, that will take up a lot of space. It seems as if ASCII is better, at least for English, as it only takes 7 bits to encode a character. Is there any way we can allow for many characters, while at the same time only encoding what we really need to encode?
The solution Unicode uses is to have three different versions, which allow for more compact encodings: UTF-32, UTF-16, and UTF-8. UTF-32 uses 32 bits to directly represent each character, so here we will face more of a space problem. UTF-16, on the other hand, uses 16 bits (216 = 65,536), and UTF-8 uses 8 bits (28 = 256).
This raises the question: How is it possible to encode 232 possibilities in 8 bits, as UTF-8 does? The answer is that UTF-8 can use several bytes to represent a single character if it has to, but it encodes characters with as few bytes as possible by using the highest (leftmost) bit as a flag. If the highest bit is 0, then this is a single character or the final character of a multi-byte character. For example, 01000001 is the single-character code for A (i.e., 65). If the highest bit is 1, then it is part of a multi-byte character. In this way, sequences of bytes can unambiguously denote sequences of Unicode characters. One nice consequence of this set-up is that ASCII text is already valid UTF-8.
More details on the encoding mechanism for UTF-8 are given in Figure 1.17. An important property here is that the first byte unambiguously tells you how many bytes to expect after it. If the first byte starts with 11110xxx, for example, we know that with four 1s, it has a total of four bytes; that is, there are three more bytes to expect. Note also that all nonstarting bytes begin with 10, indicating that they are not the initial byte.
Figure 1.17 UTF–8 encoding scheme

To take one example, the Greek character α (“alpha”) has a Unicode code value of 945, which in binary representation is 11 10110001. With 32 bits, then, it would be represented as 00000000 00000000 00000011 10110001. The conversion to UTF-8 works as follows: if we look at the second row of Figure 1.17, we see that there are 11 slots (x’s), and we have 10 binary digits. The 10-digit number 11 10110001 is the same as the 11-digit 011 10110001, and we can rearrange this as 01110 110001, so what we can do is insert these numbers into x’s in the second row: 110 01110 10 110001. This is thus the UTF-8 representation.
We now know that we can encode every language, as long as it has been written down. But many languages have no written form: of the 6,912 known spoken languages listed in the Ethnologue (http://www.ethnologue.com), approximately half have never been written down. These unwritten languages appear all over the world: Salar (China); Gugu Badhun (Australia); Southeastern Pomo (California); and so on.
If we want to work with an unwritten language, we need to think about dealing with spoken language. Or, more practically, even if a language has a written form, there are many situations in which we want to deal with speech. Picture yourself talking to an airline reservation system on the phone, for example; this system must have some way of encoding the spoken language that you give to it. The rest of this chapter thus gives a glimpse into how computers can work with speech. Even though the book mainly focuses on written text, it is instructive to see how spoken and written data are connected.
In order to deal with speech, we have to figure out what it looks like. It is very easy to visualize spoken language if we think of it as phonetically transcribed into individual characters, but to transcribe, or write down, the speech into a phonetic alphabet (such as the IPA we saw before) is extremely expensive and time-consuming. To better visualize speech and thus encode it on a computer, we need to know more about how speech works and how to measure the various properties of speech. Then, we can start to talk about how these measurements correspond to the sounds we hear.
Representing speech, however, is difficult. As discussed more fully below, speech is a continuous stream of sound, but we hear it as individual sounds. Sounds run together, and it is hard for a computer to tell where one ends and another begins. Additionally, people have different dialects and different sizes of vocal tracts and thus say things differently. Two people can say the same word and it will come out differently because their vocal tracts are unique.
Furthermore, the way a particular sound is realized is not consistent across utterances, even for one person. What we think of as one sound is not always said the same. For example, there is the phenomenon known as coarticulation, in which neighboring sounds affect the way a sound is uttered. The sound for k is said differently in “key” and the first sound in “kookaburra”. (If you do not believe this, stick one finger in your mouth when you say “key” and when you say “koo”; for “key” the tongue touches the finger, but not for “koo”.) On the flipside, what we think of as two sounds are not always very different. For instance, the s in “see” is acoustically very similar to the sh in “shoe”, yet we hear them as different sounds. This becomes clear when learning another language that makes a distinction you find difficult to discern. So both articulatory and acoustic properties of speech are relevant here; let’s now take a closer look at both of these.
Before we get into what sounds look like on a computer, we need to know how sounds are produced in the vocal tract. This is studied in a branch of linguistics known as articulatory phonetics. Generally, there are three components to a sound, at least for consonants: the place of articulation, the manner of articulation, and the voicing.
The place of articulation refers to where in the mouth the sound is uttered. Consider where your tongue makes contact with your mouth when you say [t] (t in tip) as opposed to when you say [k] (k in key, c in cool). For [t], the tip of your tongue touches the area of your mouth behind your upper teeth (what is called the alevolar ridge), whereas for [k], the back of your tongue rises to the back of the roof of your mouth (i.e., the velum).
While place makes some distinctions, there are sounds said at nearly the same point in the mouth that come out differently, due to the manner of articulation. For example, [s] (s in sip, c in nice), like [t], is an alveolar consonant, uttered with the tongue behind one’s upper teeth. However, [t] involves a complete stoppage of air (and thus is commonly called a stop consonant), whereas [s] allows a narrow stream of air to continually pass through the constriction (and is referred to as a fricative).
The final distinction involves voicing, or whether or not one’s vocal cords vibrate during the utterance. Your vocal cords are in your throat, so you can easily compare sounds by putting a hand on your throat and feeling whether there are vibrations. For example, [s] and [z] (z as in zoo) are both alveolar fricatives, but [s] is unvoiced and [z] is voiced.
While studying articulation provides important distinctions, to which we will continue to refer in the following, to represent spoken language on a computer we need speech properties that we can quantify, which brings us to acoustic phonetics. Acoustic properties of speech refer to the physical characteristics of sound. Sound waves that we speak are simply “small variations in air pressure that occur very rapidly one after another” (Ladefoged, 2005). When these waves hit a recording device, we can measure how often they hit, how loud they are, and so on.
As mentioned before, sound is continuous, but computers store data in discrete points, as illustrated in Figure 1.18, and thus can only capture the general pattern of the sound. The quality of a recording depends on the sampling rate, or how many times in a given second we extract a moment of sound. The sampling rate is measured in samples per second, commonly referred to as Hertz(Hz).
Figure 1.18 A continuous line with evenly spaced discrete points
The higher the sampling rate, the better the recording quality, though it takes more space to store. For capturing the frequencies of language sounds when using the telephone, 8,000 samples per second turn out to be adequate, and 16,000 or 22,050 Hz is often used when recording speech.
Some of the properties of speech we are interested in include the speech flow, the rate of speaking and the number and length of pauses. This is easy enough to measure in units of time (i.e., seconds). The loudness, or amplitude, is the amount of energy a sound has. Again, we have an intuitive sense of what it means to measure amplitude; loudness of sounds is typically measured in decibels.
Most important for classifying sound waves into individual speech sounds are the frequencies associated with each sound. As we will see below, the frequency – or how fast the sound waves repeat – is the basis on which we are able to tell sounds apart. Frequency can be measured in terms of cycles per second, again referred to as Hertz.
To get a feel for how sounds are represented on a computer, we start with a waveform, shown in an oscillogram. Figure 1.19 represents the word “Thursday”: as time passes on the x-axis, we can observe the changes in amplitude, or loudness, on the y-axis. All phonetic figures in this chapter were produced using Praat (http://www.fon.hum.uva.nl/praat/). The first vowel in the figure has the loudest sound and there is essentially silence in the middle of the word, due to the stop consonant [d].
The pitch of a sound – how high or low it is – provides additional information, especially for vowels. Speech is composed of different frequencies all at once (due to the way sound reverberates in the vocal tract): there is a fundamental frequency, or pitch, along with higher-frequency overtones. These overtones give unique character to each vowel. We also have intonation; that is, the rise and fall in pitch. For example, the intonation at the end of questions in English typically rises.
Figure 1.19 A waveform for “Thursday”
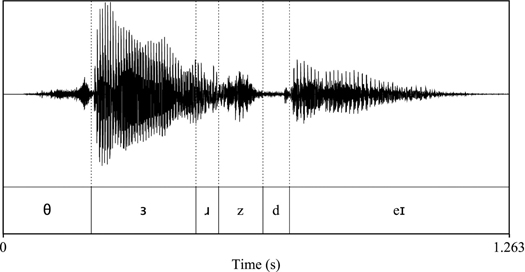
Figure 1.20 A spectrogram for “Thursday”
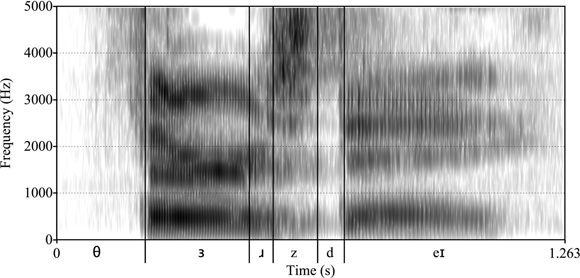
Finally, we can analyze spoken language using a spectrogram, which is a graph to represent the frequencies of speech (y-axis) over time (x-axis). As we can see in Figure 1.20, each sound is a complex unit made of different frequencies. In fact, what we observe in a spectrogram will help us the most in automatically determining what sound was uttered, to which we turn next.
A spectrogram has various measurable properties that tell us what the sounds are. Under the Hood 1 on Reading a spectrogram provides more details, but we will sketch a few general properties here. These are questions you can ask when looking at a spectrogram:
This tells us how loud each sound is and is measured in decibels. Different sounds differ in their loudness, including some sounds – such as [d] – that involve a moment of complete silence. Compare [θ] and [z] in Figure 1.20, which show that [θ] is not as loud.
The darkest lines tell us which frequencies (measured in Hertz) are the loudest and the most important for determining the sound. Each vowel has roughly three prominent frequency bands, and the vowels are distinguished by these bands. For voiced sounds, we typically also see a low dark band.
One last point involves how the frequencies change over time. When we have stop consonants like [t] or [k], there appears to be nothing in the spectrogram by which we can distinguish the sounds, and yet we make the distinction quite easily. It turns out that the transitions of the vowel bands before and after the consonant are unique.
It is these measurements that represent speech on the computer. In other words, to a computer, speech is nothing but a sequence of various numeric measurements. After we discuss reading a spectrogram, we will delve into turning these measurements of speech into text.
Figure 1.21 A spectrogram for “fuss”
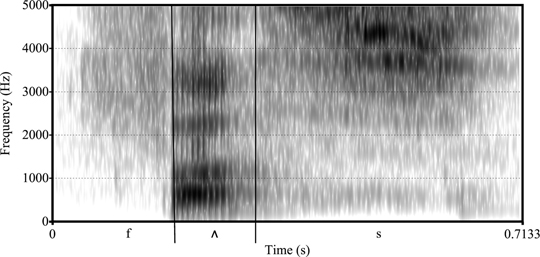
Figure 1.22 A spectrogram for “fuzz”
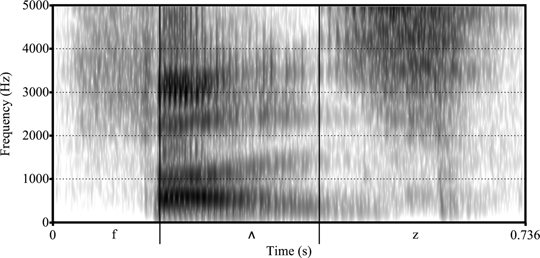
Figure 1.23 A spectrogram for “deet”
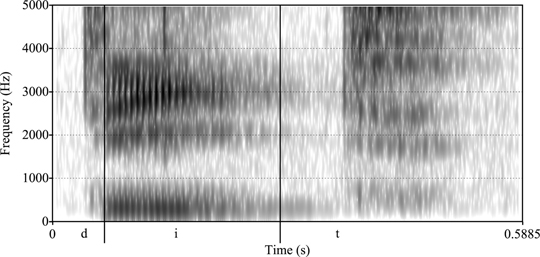
Figure 1.24 Some of the major vowels in English

Written and spoken forms of language are clearly relatable. If we can automatically relate the two, then we can perform two very practical tasks: automatic speech recognition (ASR), which maps sound to text, and text-to-speech synthesis (TTS), which maps text to sound.
Automatic speech recognition is the process by which a computer converts a speech signal to text. Such systems, are enormously practical, as they can be integrated into dialogue systems, can allow doctors to dictate patient diagnoses in one quick pass, and so on.
In general, ASR systems go through three steps. First, speech is digitally sampled, as was discussed above. As this converts continuous speech into a discrete representation, this will naturally involve information loss. Secondly, the speech samples are converted into measurable units, as was also discussed above; this is referred to as acoustic signal processing. Here, the digital samples are converted into, among other things, recognizable frequencies, giving the computer a representation of speech to work with. These frequencies are used for the third step, the recognition of sounds, groups of sounds, and words. The frequencies can be used to identify speech sounds, but, as we discussed before, the interpretation of a given frequency is often ambiguous, since different people speak differently. For example, a [t] might sound like a [d]. Thus, more sophisticated analysis will likely be added to this step; the Under the Hood section on language modeling provides more information below.
Given these basics, there are different kinds of ASR systems. The main distinction we can make is between speaker-dependent and speaker-independent ASR systems. Speaker-dependent systems work for a single speaker, whereas speaker-independent systems work for any speaker of a given variety of a language, for example American English. Given the range of pronunciations across different people, speaker-dependent systems are clearly more accurate. This is why there are also speaker-adaptive systems, which start out as independent systems but begin to adapt to a single speaker in order to improve accuracy.
We can also distinguish ASR systems based on their domain. ASR systems that are built for a particular domain, for instance flight reservations, are optimized for dealing with flight vocabulary, and their vocabulary size may be much smaller than general-purpose ASR systems.
The reverse of automatic speech recognition is text-to-speech (TTS) synthesis, which converts words into speech. This might seem like a trivial task: couldn’t we simply record a voice saying phrases or words and then play back those words in the appropriate order?
While this might work for talking toy dolls, when we deal with technology such as dialog systems (see Chapter 6), the computer system generates written sentences that need to be synthesized on the fly. Thus, we have to be able to break the text down into smaller units that can be converted into speech. This is challenging, given that writing system representations are often phonetically ambiguous.
The main idea behind speech generation is to adjust the values of the frequencies, the loudness, and so forth, to produce the correct sounds. Since we know what frequencies correspond to which vowels, for example, we can play those frequencies to make the speech sound like the right vowel. Of course, as we mentioned before, sounds are always different, across time and across speakers. One way to help in the process of generating speech is to have a database of speech and to use diphones – that is, two-sound segments – to generate new utterances. The contextual information found in diphones helps with two different issues: (i) the fact that every sound is spoken differently depending on the neighboring sounds; and (ii) the fact that phonetically ambiguous characters are less ambiguous in context.
After reading the chapter, you should be able to:
Further reading
More information on writing systems, including various graphics, can be gleaned from websites such as http://www.omniglot.com. Additionally, there are books on writing systems, such as Daniels and Bright (1996). Sproat (2000) offers a unique treatment, which focuses on computational properties of writing systems, and Sproat (2011) extends the writing system discussion to language technology and its impact on society. Both are highly recommended. Turning from writing systems to language, a thorough set of information on the world’s languages can be found in the Ethnologue (Gordon, 2005). For an accessible overview of topics related to language and how language can be studied, check out Language Files (Mihaliček and Wilson, 2011). As a reference book, you can find comprehensive information in David Crystal’s Cambridge Encyclopedia of Language (Crystal, 2011).
For an introductory look at automatic speech recognition and language modeling, the Jurafsky and Martin (2009) textbook is a valuable resource. There are also papers such as Madnani (2009) that provide good overviews of language modeling, and you can check out practical toolkits, such as SRILM (Stolcke, 2002), at http://purl.org/lang-and-comp/srilm. For thorough introductions to the field of phonetics, Ladefoged (2005) and Johnson (2003) are recommended. The latter is especially good for examining the acoustic properties of speech.