In the 1960s, if you wanted to read the news, you bought or borrowed a newspaper. If you were unwilling to spend the necessary time, you could read capsule summaries of the most important news in, for example, Time magazine’s listings section. If you were too busy, or too important, to do even that, you could arrange for someone to read the newspapers for you and give you a summary of what you needed to know. If you were a fruit grower, you could subscribe to Fruit Growers’ News and get targeted digests of the news that mattered to you.
But now, many newspapers and magazines offer you the chance to read their material online, often at no charge. This is a big change, because the text is now searchable, indexable, and available for reuse. As well as traditional newspapers, there are weblogs and aggregator sites. Aggregators pull together information from all over the web, providing a digest suitable for the target audience. Aggregators exist for tracking news about cars (www.autoblog.com), greener cars (www.green.autoblog.com), bicycles (www.cyclelicio.us), running (www.coolrunning.com), baby strollers (http://strollersandprams.com), and stationary exercise machines (www.treadmilladviser.com). Even Fruit Growers’ News is now readily available online (www.fruitgrowersnews.com), as are countless other websites and weblogs catering to specialist interests. These can be money-making ventures if they can deliver an audience that is attractive to advertisers.
Now that text is available online, we have the opportunity to add value by using language technology to process the text. The methods we study in this chapter are all about sorting documents into user-defined classes, so the techniques go by the name of document classification. You might, for example, have one class for articles about cars, another (overlapping) class for articles about environmentally friendly cars, and another for articles about fruit trees. In principle, the classes can be anything you like, but in practice you only care about classes that have some commercial or scientific value.
One of the most commercially significant uses of this technology is known as sentiment analysis. Another term that means much the same is opinion mining. The key idea is to automate the detection of positive and negative sentiments in documents. For many years companies, political parties, and pressure groups have used focus groups and audience surveys to track opinions about their products, policies, and positions. Sentiment analysis technology promises to be able to automate this process, trawling the press, internet, and social media for documents that express opinions, organizing them according to the opinions that they express, and presenting summaries of the results. This is a kind of data mining, one that makes especially heavy use of language technology.
For example, if you want to find out about the general opinion of the movie Pearl Harbor, you can check out Metacritic (www.metacritic.com) or Rotten Tomatoes (www.rottentomatoes.com) and see multiple reviews, by both professionals and lay people. The least favorable user review makes its opinion very clear:
Ridiculous movie. Worst movie I’ve seen in my entire life [Koen D. on metacritic]
This person hated it. The most positive review is equally clear:
One of my favorite movies. It’s a bit on the lengthy side, sure. But its made up of a really great cast which, for me, just brings it all together. [Erica H., again on metacritic]
However, most of the reviews for this movie are similar to Alan Scott’s from the New York Times:
The Japanese sneak attack on Pearl Harbor that brought the United States into World War II has inspired a splendid movie, full of vivid performances and unforgettable scenes, a movie that uses the coming of war as a backdrop for individual stories of love, ambition, heroism and betrayal. The name of that movie is From Here to Eternity. (First lines of Alan Scott’s review of Pearl Harbor, New York Times, May 25, 2001)
While Scott’s review finishes up being positive about the fabulous action sequence at the heart of Pearl Harbor, and very positive about From Here to Eternity (a different, and apparently much better, movie), it drips with sarcasm about everything else in the first movie. That is obvious to a human, but is difficult for a machine to spot. Here is another review that we enjoyed reading:
The film is not as painful as a blow to the head, but it will cost you up to $10, and it takes three hours. The first hour and forty-five minutes establishes one of the most banal love triangles ever put to film. Childhood friends Rafe McCawley and Danny Walker (Ben Affleck and Josh Hartnett) both find themselves in love with the same woman, Evelyn Johnson (Kate Beckinsale). [Heather Feher, from http://filmstew.com]
Most review sites use human editors to associate scores with reviews, but this is very much the kind of activity that people want to automate. Some of the automation might be quite easy: a review that dubs the film “ridiculous” and “worst” is probably negative, and one that says “favorite” and “great” is probably positive. But Scott’s clever New York Times review reads a lot like a very positive review, until you notice that the positive comments are directed at a completely different film. And Feher’s backhanded “not as painful as a blow to the head” is also likely to defeat any simple automated system.
“Painful” would be bad, “not painful” might be good, “not as painful as …” suggests that some pain is involved. “Not as painful as a blow on the head” quantifies the pain in a rather alarming way. Language is like that: the meaning twists and turns as each word is added to the next. The authors happen to find Feher’s subtle deployment of this roller-coaster effect cool and funny, but it certainly is not going to be easy for a machine to handle.
Clearly, if we can rate movie reviews automatically, we can make our own versions of MetaCritic, and maybe apply the idea to a wider range of topics than is possible when humans are in the loop. But language is subtle, so we cannot be sure that this kind of automation is going to be possible.
The movie sites are interested in telling the difference between good and bad reviews, and also in assigning a numerical score – which generally makes them semi-structured data, as outlined in Section 4.4. In general, when we are interested in assigning a label (e.g., good or bad) to a document, the task is called classification. In this chapter, we focus on document classification, and show some of the uses to which it can be put. The most important practical examples of this technology are the junk mail filters that try to protect you from the flood of unwelcome email that would otherwise clog up your inbox. They are so good that we normally hardly notice them, but when they stop working or misbehave we realize how important they are in keeping our email interactions manageable. Other uses of the technology are call-routing systems (the systems that try to send you to the best, or perhaps cheapest, person when you phone a helpline), systems for classifying texts by topic, and systems that classify documents according to their sentiment. An automated movie review site would need a really good sentiment classifier to judge whether a review is good or bad. It might also make use of a topic classifier to scan documents and decide whether they are movie reviews in the first place.
Document classification is an example of a computer science activity called machine learning. Machine learning applies not just to language, but to any situation in which the computer is expected to “learn from experience.” If we wanted, we could devote pages to discussions of whether machines can ever be said to be truly intelligent, or about the true nature of the so-called learning. We think that these discussions are interesting, and we touch on them very briefly at the end of Chapter 6, but they really belong in a philosophy class, not here.
The basic set-up for machine learning is the following: we have access to a training set of examples; we aim to learn from these examples. For the moment, think of the examples as articles from the online version of last month’s New York Times.
Our long-term goal is to use what we have learned in order to build a robust system that can process future examples of the same kind as those we found in the training set. Think of these future examples as the articles that are going to appear in next month’s New York Times. Clearly, we have a problem, because future examples are not yet available.
As an approximation, we use a separate test set of examples to stand in for the unavailable future examples. Think of these as this month’s New York Times articles. Since the test set is separate from the training set, the system will not have seen them. If the system performs well on the test set examples, it will probably also do well on the unseen future examples.
There are several important variations on this scheme, at which we take a closer look in the next sections.
In supervised learning we need the training set and the test set to have been labeled with the desired “correct answers.” Imagine that there is a news service that provides a stream of uncategorized articles, and that a newspaper needs a system that will sort these articles into separate piles for News, Sport, Arts, Business, and Do not use. The first step is to make a training set and a test set by labeling a few hundred articles with the desired categories. The second step is to apply machine learning software to the labeled training set. This produces an object called a model, which summarizes what the software has learned from the training set.
The third step is to read the trained model into the machine learning software and use it to generate predictions for the test set. Since we are testing the model’s ability to make a prediction, we do not let the software see the correct answers for the test set examples. If the software is working well and the model is good, the predictions will often be accurate. We discuss precisely how to measure accuracy in Section 5.4. It is unlikely that the model will be perfect, but it may well be good enough for our purposes. The fourth and final step is to deploy the trained model on unseen examples. It uses what it has learned to sort the articles into the necessary piles. This kind of learning could be the basis for an automated system. A newspaper might have a national news section, a local news section, a business section, and a sports section. The learning goal would be to allocate each article to the correct section. In a real-world application, there will usually be someone who is responsible for checking the results before the paper is printed, because there will almost certainly be some mistakes, no matter how good the machine learning method is.
In unsupervised learning, we assume that there are no prespecified categories. Imagine that the newspaper still has a stream of uncategorized articles, but now the task is to organize the articles into piles in such a way that similar articles occur in the same pile. In this setting, the piles are often called clusters, and the process of organizing the articles into clusters is called clustering. Clustering can be used to sort articles into groups that could be laid out on the different webpages of an online publication. In that setting, there is no need for the groups to have fixed names.
The reader will be able to notice that articles in a given cluster share something, such as being about sports, but the algorithm would be just grouping articles, not trying to name the clusters. The big plus of this approach is that you do not need a training set, so there is no costly process of going through labeling up the articles. The big negative is that the clusters might not be that intuitive. For example, if you cluster common words, one cluster often turns out to be the words “Monday”, “Tuesday”, “Wednesday”, and “Thursday”, with “Friday” off in another cluster. This is because Friday is the only weekday that frequently turns up following “Thank goodness it’s …”
When we try to classify or cluster documents, the first step is to identify the properties that are most relevant to the decision we want to make. These properties are called features. In biology, a specimen could have features like scales or gills. If you observe these features, you can be fairly confident that your specimen is a fish. In the same way, when you are trying to decide whether a document is junk mail or not, you should pay attention to features of the document that are likely to help with the decision.
If you are trying to guess whether something is junk mail, these could include things like:
None of these features is a certain indicator of junk mail, but all are strong evidence that the document is more likely to be junk than if we had not seen the feature. To make a useful system, we need to tell the computer two things. First, we have to say exactly which features are used and exactly how to detect them. Secondly, we have to specify a way of weighting the evidence provided by the features. It often works well to use machine learning to weight the evidence, rather than doing it by hand, but it is much harder to automate the first stage of deciding what evidence is potentially relevant. This first stage is often called feature engineering.
There are two common strategies for doing feature engineering. The first is to use lots of features, in the hope that some of them will be relevant and useful. We will call this the kitchen sink strategy, since we throw everything we have at the problem, including, perhaps, the kitchen sink. If you are building a junk mail detector, you could adopt a version of this strategy by using the words themselves as features: because there are lots of different words in the messages, there will also be lots of different word-based features. It is almost certain that some of these features (such as the presence or absence of the word enlargement) will be useful indicators. Of course, there will also be many irrelevant features, such as the presence or absence of the word “apple”. If we adopt the kitchen sink strategy, we will need to choose a machine learning method that is good at focusing on the few but important relevant features, and also good at ignoring the many irrelevant features. We will return to this later in the chapter, when we discuss machine learning methods in detail.
Feature engineering actually has two parts. You need to decide which features you would like to collect, then write computer code to do the work of collecting them. One advantage of using words as features is that it is almost as easy to collect and count all the words in a document as it is to collect just a selected few.
The second common strategy for feature engineering is to use careful thought to try to identify, ahead of time, a small set of features that are likely to be relevant. We will call this the hand-crafted strategy, because it demands from the software developer the same kind of careful and sustained attention to the problem that a skilled woodworker might give to the creation of a beautiful piece of furniture. The software developer uses intuition and experience to select features that seem promising. An advantage of this approach is that there will be fewer irrelevant features, so the machine learning method does not have to be as good at ignoring them as was needed when we were using the kitchen sink features. A disadvantage is that the task of choosing relevant features ahead of time is very difficult. Human beings are not good at this task. Part of the reason is that it is hard to know whether the selected features are general enough. Testing for “DR. MRS.” specifically is easy, but it is far harder to cover all the cases of similar features that might arise.
In practice, most software developers use an iterative method. They pick an initial set of features, train a classifier, measure how well it does, then try to work out which features are working well, and which less well. By analyzing the results, they come up with ideas for further features, add them in, and retry the machine learning. Depending on the problem, they might go around this cycle multiple times, until satisfactory performance is reached. The key to the success of this iterative approach, which is used on a much larger scale by firms such as Google, is to insist on systematically and thoroughly measuring success rates. With the luxury of very large numbers of users and correspondingly huge data centers, the big web firms can rapidly collect evidence about how well they are doing. This instant feedback makes it possible to try out all kinds of possible improvements, keeping only the ones that seem to work well.
Software developer time is a limited resource, so it may be better to collect a large number of easy but marginally relevant features quickly than to spend a lot of time trying to write code to extract the difficult features.
The Text Retrieval Conference (TREC) made available a sample collection of email consisting of about 57,000 junk emails and about 39,000 good emails. Computer scientists and engineers tend to call junk emails spam, for reasons that are slightly unclear, but that may involve the obsession that the Monty Python comedy team had with Hormel’s processed pork product. They also tend to call nonjunk emails ham, presumably on the basis that real ham is to be preferred to any imitation. The authors feel that the spam/ham terminology is a bit geeky, and try to avoid overusing it, but sometimes we cannot help ourselves.
When writing this paragraph, we checked and found that one of us had received 20 instances of spam and 3 of ham in the last 12 hours. All of the spam was successfully filtered out. Many people (including us) trust the filters enough that we hardly ever check for misclassified ham. We say that the false positive rate of the spam-detection task is very low (see more below on measurements).
If we are serious about spam detection, we need to be precise about how to measure success. It may seem obvious what we need to measure. We have a series of decisions to make, so we make them, and measure whether we got them right or not. If we classify all the spam as spam, and all the good mail as good, we have succeeded and all is well. Although this is definitely correct, we would be fooling ourselves if we believed that we can design a perfect system that gets every single decision correct. So we need measures that quantify our partial successes and failures and help us to build better systems.
Machine learning is a real-world science, like medicine, and we cannot always afford to wait for complete and reliable evidence to become available, so mistakes are almost inevitable. What we really want is a way of measuring performance that tells us what we need to know about ways in which an imperfect system could be improved.
To do this, we borrow some concepts and evaluation methods that were developed to meet the needs of medical science. These methods apply anywhere, but they turned up first in medicine because of the need to reason effectively with complex and uncertain data. When we run a classifier on a document to decide whether it is spam or not, it is much like running a diagnostic test to collect evidence about whether a patient has a disease or not. Here there are two two-way distinctions to be made:
So there are four possible ways the situation could be after the test has been given, as shown in Table 5.1.
Table 5.1 A diagnostic test
| Has disease | No disease | |
| Test positive | True positives | False positives |
| Test negative | False negatives | True negatives |
Perhaps the patient has the disease, and the test correctly returns a positive result. We call this a true positive. When the patient does not have the disease, and the test correctly returns a negative result, it is called a true negative. In both of these cases, the test is doing its job. But there are two other possible outcomes. The test could return a negative even though the patient has the disease. This is called a false negative and is a bad thing, because a patient who needs treatment may not receive it. The fourth possibility is that the test returns a positive even though the patient does not have the disease. This is called a false positive and is again a bad thing, because the patient is then likely to receive unnecessary treatment.
Epidemiology example You are an epidemiologist working on a disease (which means that you study health patterns across a population). You know from previous experience that about 10% of the population has the disease. You have a medical test for a disease. The solution is supposed to turn blue if the person has the disease; otherwise, it should stay clear. If the person has the disease, there is a 98% chance that the solution will turn blue and a 2% chance that it will stay clear. If the person does not have the disease, there is a 90% chance that the solution will stay clear and a 10% chance that it will turn blue.
Now suppose that you run the test and the solution does turn blue. You now know that you are dealing with either a true positive or a false positive, but you do not know which it is. Therefore, you cannot tell for sure whether the person has the disease.
It surprises most people that in this situation the probability that the patient has the disease is only a little more than 50%, since many of us have an intuitive feeling that the answer should be around 90%. If you are not familiar with this kind of probability calculation, do not worry; we will give the details later in the chapter. If you are curious about where the intuitive sense that the answer should be 90% comes from, we will discuss that too. But first, we will introduce some concepts.
The numbers in Table 5.1 are affected both by how well the test works, and by whether the disease we are testing for is rare or common. If the disease is rare, the vast majority of the patients tested will be in the second column of the table, and the first column will only have a few entries. If the disease is common, for example influenza, there will be more of a balance, with significant numbers of patients in the first column. In order to make the right decisions about how to interpret test results, medical scientists need to make a numerical estimate of how rare or common the disease is. Their best guess about how likely it is that a random person drawn from the population will have the disease is called the base rate. If we think that, at any given time, about 1 in 80 of Ohio State students will have influenza, that makes the base rate 1.25%. Since there are about 50,000 Ohio State students, our guess is that around 50,000/80 = 625 students have the flu right now.
If 1 in 80 seems low to you, remember that this is your chance of having the flu right now. Since there are about 30 weeks in the Ohio State year, and the illness takes about a week, your chance of catching it at some point in the year would be something like 30/80 = 38%.
The probability of 1 in 80 is a guess, but what is important is that by making a guess we get some feel for what might be going on. By contrast, our estimate of the base rate of yellow fever among the same population is 1 in 250,000. This means that we think it is rather unlikely that even one student has yellow fever right now. This number is also a guess.
The airport security line The analysis in Table 5.1 applies to many nonmedical situations, including the security line at airports. Suppose there is a scanner that is designed to detect guns in passenger baggage. Imagine that you are in charge of designing a sensible policy about how to use the scanner and interpret the results.
Medicine uses two standard measures to assess the value of a test. An overview of these measures, and their relationship to false and true positives, is in Table 5.2.
Table 5.2 Measures of a diagnostic test
sensitivity
The first is called sensitivity. This is the ratio
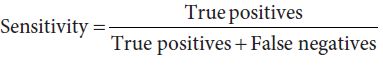
which focuses on what happens when the patient does really have the disease. Sensitivity is high when true positives massively outnumber false negatives; if you get a negative result in a high-sensitivity test, you can be pretty sure that you do not have the disease. In computational linguistics, we usually call sensitivity recall, as we discussed in Section 4.3.2. Precision corresponds to the positive predictive value, and the calculations are the same. If you know that your search engine typically has high recall, and your search for fifty-year-old boy bandsproduces no results, you can be pretty sure that there are no relevant documents out there. Sensitivity is important for ruling out the disease, and for making sure that people who do have the disease get treated, but it says nothing at all about what happens to patients who do not have the disease. So, the picture is incomplete.
A second measure, which focuses on what happens when the patient does not have the disease, is called specificity. This is the ratio
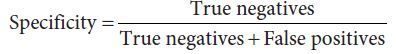
Specificity will be high if true negatives massively outnumber false positives. The higher the specificity, the fewer the number of healthy people who will be subjected to follow-up tests.
Errors in medical tests Let us now revisit the question about medical diagnosis that was posed earlier. Suppose that you have a medical test for a disease. It has 90% specificity and 98% sensitivity. The base rate of the disease among the population tested is 10%. You test 1,000 patients.
The questions we need to answer are:
On average, we expect that about 100 patients will have the disease and 900 will not. So we expect to see around 100 × 0.98 = 98 true positives, 100 × (1−0.98) = 2 false negatives, 900 × 0.90 = 810 true negatives and 900 × (1−0.90) = 90 false positives, as in Table 5.3.
Table 5.3 Expected numbers if you do 1,000 tests
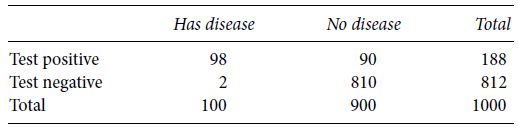
Notice the following:
Remember that there are four possible situations:
To find out how likely it is that you really have the disease if you have a positive test, we need to consider the ratio between the probability of a true positive and the probability of any kind of positive. In the formula below, the numerator is the probability of getting a true positive and the denominator is the probability of getting either a true positive or a false positive. The result is the probability of having the disease, given that you got a positive test, which is what we want.
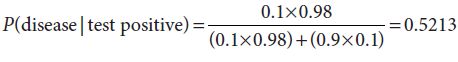
The probabilities of false negatives and true negatives are not needed for this calculation, because we know that the test came out positive. They would be needed if you wanted to calculate the probability of having the disease after a negative test.
If this problem was new to you, and you used your intuition when we first asked the question, it would not be at all unusual to be surprised by the estimate of 52% as the probability of having the disease given a positive test. This is because there is a cognitive bias called base rate neglect, which tends to make human beings ignore the effect of the base rate and focus far more on the connection between the symptoms and the disease. This leads us, almost without noticing it, to assume that about 50% of the people to whom the test is administered have the disease and the other 50% do not. If you do the calculation again, this time under the assumption that the base rates are equal, you will get:
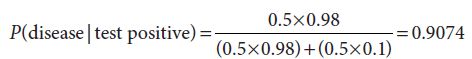
which will lead you to believe that nearly 91% of the people with a positive test are going to have the disease. In the same way, it is easy to fall into the trap of unintentionally assuming that the airport scanner sees about 50% terrorists and 50% nonterrorists. Unless you are particularly paranoid, next time you are in the line at an airport, you will be able to look at the people around you and decide that you really do not believe that 50% of them are terrorists. But, even knowing this, it is not easy to adjust your feelings about risk to match what you know to be true about the situation.
As you may have realized in thinking about the extended example on medical diagnosis, a third factor comes into the evaluation of a medical test. It is not enough to know how well the test works and how common the disease is, we also need to assess the costs and benefits of the various options available to us. To show how this works, we are going to use a simplified version of the calculations that a real doctor would need to do. To keep things gentle, we will say that the disease is always curable and that nobody ever dies of it. However, there are two different treatments: treatment A is cheap, costing the hospital $10, but treatment B is expensive, and would cost the hospital $1,000. For simplicity, and because we like the idea, we are going to say that the patient pays nothing, and the cost is all on the hospital. Treatment B will work any time, but treatment A works only in the early stages of the disease. The point of the test is to find people who should get treatment A now. The hospital’s policy is to apply treatment A whenever the test comes back positive. It costs the hospital an unnecessary $10 whenever there is a false positive. We say that the payoff for a false positive is −$10. The payoff for a true positive is also −$10, because the hospital pays for the treatment in that situation too.
However, if the test misses a patient who does have the disease, that person will eventually come back in and require treatment B, which is much more expensive. So, the payoff for a false negative is −$1,000. The payoff for a true negative is $0, because no treatment is needed. In a real hospital situation, life would be more complicated, because there would be another choice to be made before this all happened: the doctors would have to consider the cost of the test itself. They might decide that some people are so unlikely to have the disease that it isn’t even worth running the test.
Table 5.4 The payoffs for the four outcomes
| Has disease | No disease | |
| Test positive | − $10 | − $10 |
| Test negative | − $1,000 | $0 |
At this point, you are probably wondering whether this book has been taken over by medical researchers, biologists, or Homeland Security types. Not exactly, because the ideas we have used so far apply to document classification, too. In document classification, high specificity means that few of the irrelevant distractor documents will be classified into the target class. If the target class is junk emails, this means that few nonjunk emails will be placed in your junk mail folder. Similarly, high sensitivity means that few relevant documents will be missed.
Errors in junk mail filters If you are using this book in a class, at some point the instructor is likely to ask you to spend five minutes discussing junk mail with your neighbor. Here are some questions to think about:
Most of the applications that we have looked at so far rely on some kind of technology for distinguishing between different kinds of documents. In this section of the chapter, we explain some of the tools that are used to do this.
In the earlier sections of this chapter, we talked about the need to collect and assess evidence about the appropriate classification for documents. The crucial technical decision is to choose an appropriate algorithm for weighting the evidence. One simple and effective algorithm is known as the Naive Bayes classifier. We start by explaining the idea and then justify the math.
When we use the Naive Bayes classifier to classify documents, we run a competition between the hypothesis that the document is a piece of junk mail and the alternative hypothesis that it is not. This is expressed in math by doing a probability calculation for each of the two hypotheses. It is the evidence we collect that allows us to decide between these two hypotheses.
An example of the kind of data used in this calculation is given in Table 5.5. In order to make the example manageable, we are going to pretend that there are just a few words for which we have collected statistics. In reality, there would be many more. We have imagined an email user (we will call this user Sandy) whose usual mail conversations include recreational chat about horses, unicorns, and similar creatures, but who also gets some of the usual kind of spam. Sandy does not want genuine messages from friends (including particular friends Alice, Seth, and Emily) to be filtered out. Messages that mention rideable animals are usually good, but some of the ones mentioning stallions are suspect.
We are going to see some words that bias us to believe that the document is spam, and others that make us think it is not. The classifier needs a policy for how to reconcile the conflicting evidence.
The simplest policy is to pretend that we are dealing with a completely unstructured collection of words. We ignore the fact that the words were arranged into a particular order and that they go together to form sentences and paragraphs. All we worry about is which words occur in the document and how often they occur. This is done because it simplifies the math, not because it is realistic about how language is used. Computer scientists refer to this simplification as the bag-of-words assumption (see also Section 7.7 on word alignment).
Imagine that we cut up a document and put the words in a bag. The document might be spam, or it might not. Now, we draw the words out of a bag one at a time. Each time we see a word, we ask whether that word is more likely to have come out of a document that is spam, or more likely to have come out of a document that is not spam. We can turn this idea into math using Table 5.5 and some simple reasoning.
Table 5.5 Some evidence from Sandy’s email collection
| Spam | Ham | |
| Cash | 200 | 3 |
| Alice | 1 | 50 |
| Seth | 2 | 34 |
| Emily | 2 | 25 |
| Viagra | 20 | 0 |
| Credit | 12 | 2 |
| unicorn | 0 | 5 |
| Cookie | 1 | 5 |
| hippogriff | 0 | 18 |
| Pony | 9 | 50 |
| stallion | 3 | 8 |
| TOTAL | 250 | 200 |
For concreteness, imagine that the word that came out of the bag was “Emily”. We are also going to pretend temporarily that the words in the table are the only ones that exist. We have seen this word in a spam document 2 times, out of a total of 250 spam words overall. This means that we can reasonably estimate that we are likely, on average, to see “Emily” 2 times in 250 (or 1 time in 125, or 0.8% of the time) if the document that we put in the bag was spam. We have seen the same word 25 times in Sandy’s real messages, out of a total of 200 nonspam words overall. So, we can guess that we are likely to see the word 25 times in 200 (or 1 time in 8 or 12.5%) if the document is not spam. Since 12.5% is much bigger than 0.8%, we think, from seeing just one word, that the document in the bag is much more likely to be ham than spam. We can keep track of this by recording the odds ratio for ham to spam as 12.5/0.8, or nearly 16. This is much greater than 1, which means that we think the document is ham.
Suppose that the next word is “credit.” The counts for this are 12 in 250 for spam, 2 in 200 for ham. The odds ratio for this word is 2/200 against 12/250, or about 0.29. This is less than 1, so we think, on the basis of this word alone, that the document in the bag is probably junk.
To combine the evidence, we multiply the ratios, 16 × 0.29 = 4.63, and decide, because the combined ratio is greater than 1, that the two words together indicate a genuine document and not junk. We carry on in the same way, calculating a ratio for each new word as it comes out of the bag, and multiplying it into the combined ratio. Once we have put all this evidence in place, we can make an overall decision about the document. If the final value of the combined ratio is greater than 1, we claim that the document is genuine email; otherwise, we rate it as junk.
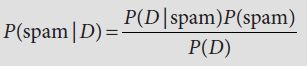
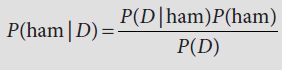
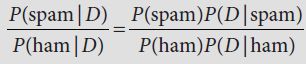
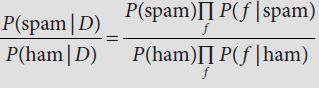
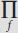. means “product over all features f.” This tells you to multiply together the probabilities for each of the individual features, one time (in the numerator) for spam, one time (in the denominator) for ham. (If you recall your algebra classes you might remember the corresponding 
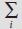notation for sums. 
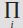is just the same as this, but for products.)The Naive Bayes classifier depends on counting things that occur in the test set. A different approach to machine learning is the perceptron, which is based on the idea of error-driven learning. The perceptron maintains a collection of weights, where each weight links a feature with an outcome. The perceptron learns from experience by trying to predict outcomes, then adjusting the weights when it makes a wrong prediction. Initially, the weights are uninformative and the perceptron is just guessing, but over time the perceptron builds up an ability to associate features with outcomes in a useful way.
Figure 5.1 The perceptron
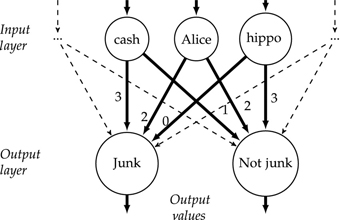
The perceptron (see Figure 5.1) is a network with two layers. The input layer has one node for each possible input feature. In our running example of Sandy’s email, there would be one node for each of “cash”, “Alice”, “Seth”, “hippogriff”, and so on. This would be unwieldy to draw in full, so we content ourself with three nodes in the diagram. The output layer contains one node for each possible outcome (in the case of Sandy’s email, one each for junk and not junk, exactly as in the diagram). The edges that link the input and output layer are associated with weights. In order to do a prediction, the perceptron reads a document and notes which words are present. We turn the nodes that correspond to these words on, and turn the others off. The role of the weights is to decide how strongly to transmit the activity of the active nodes to the output layer. Suppose that exactly three nodes (“cash”, “Alice”, “hippogriff”) were active in Sandy’s perceptron, and the weights linking these words to junk and not junk are as in Table 5.6.
Table 5.6 Weights for a perceptron
| Word | Junk | Not junk |
| cash | 3 | 1 |
| Alice | 2 | 2 |
| hippogriff | 0 | 3 |
Under this supposition, the total activity of the junk output node would be 3 + 2 + 0 = 5 and that of not junk would be 1 + 2 + 3 = 6, so not junk would win. If this prediction is right, Sandy’s perceptron can stay as it is, but if the message is actually junk, then the weights need to change.
Let us suppose that this is what happens. The perceptron algorithm changes all the relevant weights a little, in such a way as to move the result closer to a correct prediction. So it would increase the weight of “cash” (and each of the other two words) as a predictor for junk, and downweight it as a predictor for not junk. A possible result (if “a little” is taken as 0.01 for the sake of demonstration) would be as in Table 5.7.
Table 5.7 Adapted weights for a perceptron
| Word | Junk | Not junk |
| cash | 3.01 | 0.99 |
| Alice | 2.01 | 1.99 |
| hippogriff | 0.01 | 2.99 |
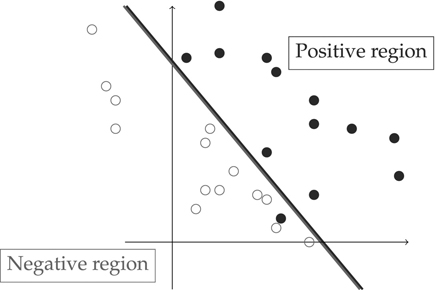
This weight change is not enough to change the prediction, but it does move the result in the right direction (not junk still wins, but not by so much). To train the perceptron, we go through the training corpus, presenting each example to the current version of the perceptron, and adapting weights whenever we make a mistake. When we get to the end of the training corpus, we start again at the beginning. Each round of this process is called an iteration. After a sufficient number of iterations, the weights will change enough that some of the predictions will flip. Gradually, the mistakes tend to go away (not completely, but to a reasonable extent). This is a result of the feedback mechanism under which features that contribute to wrong predictions get their weights changed. There is a mathematical proof that the perceptron will give perfect performance on the training set if that set has the mathematical property of being linearly separable. In two dimensions, the idea of linear separability is that a dataset is linearly separable if it is possible to draw a straight line that has all the positive examples on one side of the line and all the negative examples on the other.
In three dimensions the line turns into a plane, and in four or more dimensions it turns into a mathematical object called a hyperplane. However, the idea is always that all the positive examples are on one side and all the negative examples are on the other. In Figure 5.2, positive examples are represented by hollow circles and negative examples by filled circles. The diagonal line is a nearly perfect linear separator, as only one positive example is on the wrong side of the boundary and the rest are correctly separated. For this dataset, this is the best that any linear separator can do.
In practice, as well as in the example shown in Figure 5.2, perfect performance is rare, because real world problems are usually not linearly separable, so some misclassifications remain, and training is stopped when the number of remaining mistakes has stayed stable for long enough. When this happens, we are probably doing as well as possible on the training set, but this does not give us certainty about how well we will do on an unseen test set. If the test set and the training set are similar enough, a perceptron that does well on the training set will also do well on the test set. Unfortunately, we are not completely sure how similar the test set will be, so there is an element of uncertainty in our guesses about how well we will do.
The perceptron is an algorithm for training a linear model. The technical details of how linear models work would take us too far afield, but the discussion of linear separability above is part of the story. The final weights can be understood as saying something about the importance of each piece of evidence in a combined solution to the classification problem. When there are a large number of potentially useful features in a classification problem, researchers have discovered that linear models often work well. The perceptron algorithm is not the only way of training linear models, or necessarily the best, but it is a good starting point for exploration.
Figure 5.2 Linear separability
The main reason for including a brief discussion of the perceptron is to show that there is more than one way to do machine learning. Intuitively, the idea of collecting statistics over a collection of examples is very different from maintaining a collection of weights that are updated in a mistake-driven way. But at a deeper level, both of these approaches are supervised learning, and it is likely that they will perform similarly a lot of the time. Usually, the most important part of a machine learning solution is the choice of features that provide information on the distinctions about which we want the classifiers to learn, and the choice of classifier plays an important but secondary role. Our advice is to try a few off-the-shelf classifiers and choose the one that seems to be working best for your problem. A toolkit containing state-of-the-art implementations of many classifiers is Weka (http://en.wikipedia.org/wiki/Weka-(machine-learning)), which is written in the programming language Java and is fairly easy to use.
Weka also contains software for predicting numeric continuous values, such as the numbers of stars in a movie review (here we are imagining that the movie review site produces really detailed ratings, not just whole numbers of stars, and that the rating could be a decimal like 3.72). Predicting continuous values from features is called regression. By contrast, the perceptron and Naive Bayes produce predictions from a fixed set of discrete values, often just yes or no. Programs that predict discrete values are called classifiers in the machine-learning literature, and the term classification is used when it is important to make clear that they are predicting discrete rather than continuous values.
Another way of making our general point is that the choice of classifier should be based on thinking about the context of use of the technology. While programmers will certainly care about the details of how the algorithms work, users and managers will care more about what the system can do, what kind of errors it will make, and how this fits in with the real-world needs of the organizations or other clients who want to use the technology. One of the reasons for the substantial emphasis on evaluation in this chapter is that good evaluation focuses attention on the tradeoffs that are involved in using technology to the full. In the final section of this chapter, we provide a brief case study to illustrate how document classification technology is actually deployed. The important lesson is not that the authors think the technology is cool, although we do, but that we think it is useful for finding good solutions to real-world problems.
In the early 2000s, companies such as Lexalytics, Attensity, and Scout Labs began to offer software and services for opinion mining. Starting at about the same time, there have been many academic papers on sentiment classification. These use several different techniques, some of them very sophisticated. Figure 5.3, for example, shows the result of an analysis by Lexalytics.
Figure 5.3 Positive+ and negative− phrases detected by Lexalytics
Lexalytics is well aware that sentiment classification is never going to be perfect. But neither are spelling correctors, internet searching, or spam filters. The advantages come when you are working with large volumes of data, or when you are doing other things that human beings find boring or complicated. One of the company’s ideas is to concentrate on monitoring of sentiment, and on comparisons between the client’s business offerings and those of its competitors. For example, it is easy to find public reviews of hotels in Las Vegas, but these reviews will mix up:
Table 5.8 Comparison of hotels by category
Only the third kind of comments is truly of interest to the hotel manager. This is a fact about what the hotel manager is looking for, not a fact that is evident from the reviews themselves. But Lexalytics understands what the hotel manager will be looking for, so rather than just counting positive and negative words in the whole article, the software can search the review site for sentences that say something specific about:
A point-by-point comparison could look like Table 5.8.
This might not mean that customers of Hotel Y were systematically less happy than those of Hotel X, but it could (and in this case did) mean that the unhappy customers of Hotel Y were much more inclined to write very negative reviews than those of Hotel X. Both hotels are in the same location on the Vegas strip, but in fact Hotel Y is very famous as a super-luxury hotel. The conclusion drawn by Lexalytics was that Y’s unhappy customers, who are small in number but very vocal in their outrage, were expecting more, and felt even slightly negative experiences more keenly than did X’s. Presumably Hotel Y can react to this by working especially hard on training staff to notice, acknowledge, and fix potentially negative experiences when they happen. By being nice to a few customers who are extremely irritated, the hotel can dramatically improve its public image.
Using insight and simple quantitative reasoning, sentiment analysts are able to provide information that is useful to businesses and others, even though the underlying document-classification techniques will make mistakes in detecting positive and negative words. Provided that the general trend is well enough represented, managers can use these kinds of techniques to gain insight and plan future service improvements. Comparisons can also be made week to week, to see whether satisfaction levels are changing. It remains important to keep a human in the loop, because blindly relying on the algorithms could be seriously misleading. Notice that the conclusion about Hotels X and Y depended on insight about how customers might be reacting, not just on the data or the mathematics. The theory of machine learning provides an understanding of the technology – which you need – but intelligent common sense is just as important. Add sensible experimentation and measurement, and you have a set of powerful tools for understanding the world.
After reading the chapter, you should be able to:
Further reading
The statistical approach to junk mail filtering was popularized by Paul Graham’s “A Plan for Spam” (http://www.paulgraham.com/spam.html). His article is an excellent starting point for learning about the technology and sociology of the junk mail phenomenon. Pang and Lee (2007) is a comprehensive introduction to opinion mining and sentiment analysis. The setting for the exercise about airline complaints comes from the infamous “United breaks guitars” incident (http://www.huffingtonpost.com/2009/07/24/united-breaks-guitars-did_n_244357.html). The discussion of base rate fallacy is based on Bar-Hillel (1980). Cognitive biases are discussed both in the psychology literature and in the relatively recent growth area of behavioral economics.