Chapter 4
Quadratic equations
A quadratic equation is one involving a squared term and which, when all terms have been moved to the left-hand side, takes on the form ax2 + bx + c = 0. Quadratic equations are as old as mathematics itself, with examples appearing in ancient Babylonian tablets from over 4000 years ago. What is more, although lacking modern notation, these ancient mathematicians seemed to be well aware of the principles involved in solving them. Quadratic expressions are central to mathematics, and quadratic approximations of all kinds are tremendously useful in describing processes that are changing in direction from moment to moment.
The way to tackle quadratic equations is normally taught in three stages. The first looks at simple examples and tries to factorize the quadratic expression into two linear factors, which then allows you to write down the two solutions (for normally there are two). This seems to be guesswork, trial and error if you like, and so not satisfactory. Next, a mathematical device is introduced called completing the square, which allows solution of any particular quadratic. This is the general method of the ancients, although the key step may seem at first to be a little unnatural. Finally, completing the square is applied to the general equation to derive the famous quadratic formula that allows us to plug the three coefficients into the associated expression, which then provides the solutions. This formula often represents the first sophisticated piece of algebra that a student meets.
Although the quadratic formula solves every quadratic, there is much to be learnt from the other approaches apart from just methods to solve the equations, as will now be explained.
Factorization and completing the square
Let’s begin with the equation x2 − 5x + 6 = 0. The idea is to find a factorization of the expression as x2 − 5x + 6 = (x − r)(x − s), for then the two solutions of our equation will be the numbers r and s, known as the roots of the equation. This is because, when we substitute x = r into this factorized expression it returns (r − r)(r − s) = 0(r − s) = 0 and, similarly, substituting x = s into this product also gives the desired output of 0, while no other numbers apart from r and s can do this. But how are we to find r and s?
The next step represents an important idea. We expand the expression (x − r)(x − s) to give it the same form as the original quadratic expression and then choose r and s to match the corresponding coefficients. Now,
We equate the two expressions to hand:
so we need to find r and s so that r + s = 5 and rs = 6. A little thought will lead to the result r = 2, s = 3, which is to say that x2 − 5x + 6 = (x − 2)(x − 3), so the solutions of our original equation are x = 2 and x = 3. This works—substituting either the number 2 or the number 3 into x2 − 5x + 6 does indeed give zero.
The idea here is to take the quadratic expression x2 − bx + c and write it in the form (x − r)(x − s). Expanding the latter expression and matching coefficients then gives a pair of simultaneous equations in the two unknowns r and s, one of which, r + s = −b is linear, but the other, rs = c, is not. We might try to solve these equations by substituting s = −r − b into the second equation, rs = c, but that leads us in a circle back to the original quadratic equation, so this approach has serious shortcomings.
Clearly we need a better method, but before moving on it is worth noting that this sum-and-product formulation is equivalent to the original equation, and indeed this was the way these questions were often posed in classical texts, as they arise through the problem of determining the dimensions of a rectangle given its area and perimeter. With this kind of formulation, the problem was bound to have positive solutions, which were the only quantities that the ancients recognized as true numbers. For example, let us suppose that the perimeter of the rectangle is given as 28 units and the area as 48 units2. Let r and s denote the unknown dimensions of the rectangle, giving us the pair of equations
From the linear equation we infer that s = 14 − r, and substituting accordingly into the area equation yields
Instead of guessing and checking, we may complete the square to solve this quadratic. Compare the LHS, r2 − 14r, to the general expression r2 − 2ry + y2 = (r − y)2. The first two terms have the right form but the final term, y2, is missing. We may, however, force our expression to have the desired form by adding the absent term, although in order to retain a correct equation we add that term to the RHS as well to keep it balanced.
Specifically, here we will need to match −14r with −2ry so that −14 = −2y; hence y = 7 and its square is y2 = 72 = 49. This is the magic ingredient that when added to both sides allows us to take square roots:
which is to say r = 7 ± 1.
Therefore we get that either r= 7 − 1 = 6, whereupon s = 14 − r = 14 − 6 = 8, or r = 7 + 1 = 8 and s = 14 − r = 14 − 8 = 6. Either way we are led to what is essentially the unique solution, that being a 6 × 8 rectangle.
The overall approach to completion of the square is as follows. Given any quadratic equation ax2 + bx + c = 0 with a ≠ 0, we first divide through by a to get a monic equation—one in which the coefficient of the highest power, x2, is 1. This is an equivalent equation, so it follows that if we can solve any monic quadratic equation, we can solve them all, and so there is no loss of generality in confining ourselves to equations that can be written in the form x2 + bx = c. We can complete the square on the LHS by adding the square of b/2 (and not of b) because
as the cross-term that emerges when this square is expanded is 2 ⋅ (b/2)x = bx, as it needs to be. Hence, by adding this particular square to both sides, we have a new form of the equation in which the LHS is an explicit square. We now take square roots (both positive and negative) and make x the subject of the expression to finally get to the roots.
It should be appreciated that there are other interesting questions that arise involving quadratic expressions, and completion of the square allows us to answer them. We give two examples.
6. Comparing the graphs of y = x2 and y = x2 + 6x + 13.
The curve described by the equation y = x2 is the standard upward-opening parabola that has the y-axis as its axis of symmetry, and its vertex is the origin (0, 0). How does the graph of the equation y = x2 + 6x + 13 compare with that of y =x2? (See Figure 6.)
By completing the square, we can show that the two curves are identical; the difference is just that the second graph has been translated to another position, which we can describe precisely. Since
and 32 = 9, we may complete the square as follows:
Now the minimum of y = (x + 3)2 is 0, which occurs when x = −3: overall, the graph of y = (x + 3)2 is that of y = x2, only moved 3 units to the left. To obtain the graph of y = (x + 3)2 + 4, we now move the graph of y = (x + 3)2 by 4 units in the positive y-direction. In summary, the graph of y = x2 + 6x + 13 is realized by shifting the graph of y = x2 by 3 units to the left and 4 units up. In particular, the turning point of this parabola rests at (−3, 4).
Our second problem is to find the number x that most exceeds its own square. This is to say, we wish to find the value of x that maximizes x − x2 or, what is the same, that minimizes its negative, x2 − x (Figure 7). Completing the square for this expression requires us to add (and then subtract)
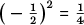. We then have
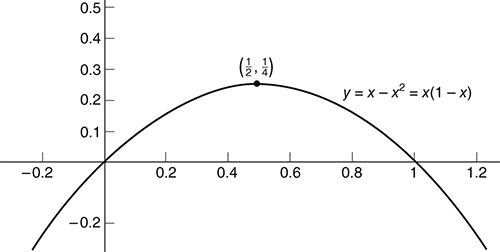
7. Graph of y = x − x2.
We minimize this quantity by making the square as small as possible, which is to say 02, and this is done in this case by putting
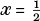. That then is our answer:
is the number that most exceeds its own square. We may note that
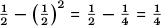and any other number exceeds its square by a lesser amount—indeed, for any number x outside the interval 0 ≤ x ≤ 1, x is actually less than x2.
As a final example in this section, let us solve
A natural impulse is to rid ourselves of the awkward square root through squaring, but doing that immediately would not work, as the root would come back to haunt us in the cross-product that arises in the square of the LHS. Instead, we focus our attack on the root by first making it the subject of the equation. Only then do we square:
hence x2 − 23x + 120 = 0 and so (x − 8)(x − 15) = 0,
which gives the two solutions x = 8 and x = 15. However, if we test these solutions, only one of them works in the original equation,
:
What has gone wrong here is that the squaring of both sides of the equation has introduced extraneous solutions, for the implication sign cannot be reversed: in general, a = b ⇒ a2 = b2, but a2 = b2 ⇏ a = b, but only that a = ±b. The extraneous solution, 15, represents the solution to the equation
.
The general point that needs to be appreciated is that if we carry out an operation on both sides of an equation that cannot be reversed, then the new equation is not equivalent to the original. Any solution of the original equation will nonetheless be contained in the solution set of the new equation. Therefore, having solved the new equation, we need to test the solutions on the original as not all of them will necessarily apply.
The quadratic formula
Applying the method of completing the square to the general quadratic equation yields the general quadratic formula, which solves the entire class of problems in one fell swoop. Quite naturally, this chapter culminates in this derivation. The slickest way to produce the formula comes through building up the RHS to the required expression as directly as possible. This begins by writing the equation as ax2 + bx = −c, multiplying throughout by 4a, and then adding b2 to both sides to complete the square on the left. In detail, we have
This derivation avoids any fractional terms until the very last line, although the argument is based upon knowing where we are headed.
It is worth studying another derivation that introduces a more general approach that may apply to other problems. The following method does not require an inspired observation as to how to manufacture squares when we are not given them in the first place, but rather the completion emerges from the algebra itself. Again we begin with the general quadratic equation, ax2 + bx + c = 0 with a ≠ 0. We make the substitution x = y + t, where t is a constant to be specified. When we make this substitution, the coefficient of y will involve t and the other coefficients. If we then choose t so that the term in y vanishes (because its coefficient is 0), we will have an equation of the form y2 = k for some constant k, from which point we may solve through taking square roots. With this in mind, we now put x = y + t. Upon rearranging the order of the terms that arise through the expansion, we obtain:
We now choose t so that the multiplier of y is 0, which is to say that the special value of t we seek comes about by putting
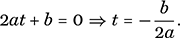(13)
The term in (12) involving y2 is ay2, while by making use of (13) we get the following for our constant term k:
We now have a clear path to the general formula, for we have reduced our original equation to ay2 + k = 0. Writing this as y2 = −k/a, we have
Rewriting y as x − t = x + b/2a and then taking square roots, the previous equation now gives
(14)
The Indian mathematician Brahmagupta (ad 597–668) seems to have been the first to explicitly describe the general quadratic formula, albeit in words, in his treatise Brāhmasphuṭasiddhānta, published in ad 628. Earlier still, Diophantus adopted a recognizably algebraic approach to such problems in the 3rd century ad. (The solutions of Euclid, some six centuries earlier, represented the roots geometrically.) The formula was, however, first stated in the modern form in 1594 by the Flemish mathematician Simon Stevin (1548–1620), who also brought decimal calculation into common usage in Europe.
As an example that leads to a quadratic the roots of which are not integers or fractions, we shall find the dimensions of the Golden Rectangle, which is defined as the rectangle that has the property that when the largest possible square is removed from the rectangle, the smaller rectangle that remains is similar to the original, meaning that both rectangles have the exact same shape, the only difference being one of scale (Figure 8).
8. Golden Rectangle.
But what is that scale? If we take the shorter side of the parent rectangle as 1 unit and the long side as x, we have from the given similarity condition that
Applying the quadratic formula (14) to the equation of (15) requires that we put a = 1, b = c = −1 and so we obtain
and since the positive solution is the one we want, we find that the Golden Ratio, often denoted by the Greek letter ϕ, is given by
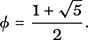(16)
The Golden Ratio arises persistently throughout mathematics, especially in the context of self-similarity problems.
We end this section by examining the number of solutions a quadratic equation may have. If we graph the function y = ax2 + bx + c, the solutions of the corresponding quadratic equation y = 0 tell us where that graph meets the x-axis. Of course, the graph may not cross the axis at all.
9. Three quadratic graphs exhibiting 0, 1, and 2 roots, respectively.
It all depends on the discriminant Δ = b2 − 4ac, which is the term that lies under the square root sign in the quadratic formula (14); in the monic case, Δ = (r − s)2, the square of the difference of the roots. The quadratic has two solutions if Δ > 0 but no solutions if Δ < 0, as there is no square root of a negative number. If Δ = 0, however, there is a unique solution, that being x = −b/2a, in which case the corresponding graph just touches the x-axis at this point, with the axis being tangent to the curve (see Figure 9). We close with a problem that showcases this transitional case.
A man, running at constant speed υ, tries to catch an old-fashioned London bus (of the kind that you could leap on while in motion) (Figure 10). When he gets within a distance d of the door, the bus, which has been stationary, begins moving away from him with constant acceleration a. What is the maximum value of d that will allow our man to catch his bus?
Let us take the origin, O, from which we measure the position of both man and bus to be the man’s initial position as the bus begins to move. At time t he will have travelled a distance υt in the positive x-direction. The speed of the bus at time t, however, is at. Since it started from rest and the acceleration is constant, the average speed of the bus in the time interval from time 0 up to time t is
. Hence the distance of the door of the bus from the origin at time t is
.
10. Man running for a bus.
Now, the runner will be at the same position as the door at the times when these two expressions for the position of man and bus agree, which is to say when the time t satisfies
(17)
We could now find these times by solving the equation (17), which is a quadratic equation in the variable t of time. However, that was not the question. Take a moment to think what is physically possible here.
Suppose there are two solutions to (17). The earlier of the two times would represent the moment when the man catches up with the bus. If he decided not to get on the bus at this point, he would overrun the door. However, since he is running at constant velocity and the bus is accelerating, eventually the bus would catch up and pass him by. The second solution is the later point when the bus door would pass him, offering him his last chance to hop on board. If, on the other hand, the values of d and a are too great, he never catches the bus and (17) has no solutions. These two scenarios correspond to Δ > 0 and Δ < 0, respectively. If the values of a and d are small, the man will catch his bus easily and the second coincidence will be quite far down the road. As we increase a and/or d, the moments of opportunity to board draw closer to one another, and at the point where Δ = 0 they merge into a single precious moment. The question then asks us to find, for a given value of a, what is the value of d where there is just one solution to (17). To determine this value, we just need to set Δ = 0. First, let’s find Δ for our equation (17):
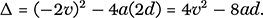
Putting Δ = 0 now gives the critical value of d:
The would-be passenger will catch his bus as along as d ≤ υ2/2a. For example, if the man is running at 6 m/s and the bus is accelerating at 1 m/s2 then the critical value is d = 62/2(1) = 18, so if the initial gap between him and the door is more than 18 m, then the bus gets away.
Having solved linear and quadratic equations, our next step would seem to be the solution of equations involving cubes and higher powers. Prior to that, however, we shall look at the algebra of polynomials and how it compares to that which governs the number system in order to see what may be learnt in general about equations involving powers higher than 2.