Torsional Contact

This chapter is dedicated to contacts between a rigid, rotationally symmetric indenter and an elastic half-space, which are subjected to a twisting moment along the z-axis in the normal direction of the half-space. The fundamental equations of elastostatics exhibit an interesting property; that purely torsional problems are generally elastically decoupled in cases of rotational symmetry. This means that the tangential displacements $u_{\varphi}$ in no way affects the radial and normal displacements. (Note regarding the notation in this chapter: contrary to the previous chapter, the word “tangential” refers to “circumferential direction” in this chapter. With this in mind, all tangential displacements will be denoted by u with the corresponding index of the tangential direction, i.e., $u_{x}$ , $u_{y}$ , $u_{\varphi}$ , etc. Normal displacements will retain the notation w.) However, in spite of the elastic decoupling, there exists the coupling caused by friction. We initially consider contacts without slip, which accordingly are decoupled from the normal contact problem, and we subsequently examine finite coefficients of friction.

5.1 No-Slip Contacts

5.1.1 The Cylindrical Flat Punch

Twisting a rigid flat punch of radius a that is in no-slip contact with an elastic half-space (see Fig. 5.1) results in the tangential displacements caused by the rigid body rotation of the punch by the torsion angle ${\varphi}$ :

$u_{\varphi}(r)=r\varphi,\quad r\leq a.$

(5.1)

The torsional stresses $\sigma_{\varphi z}$ in the contact area and the outer displacements $u_{\varphi}$ are given by:

$\begin{aligned}\displaystyle\sigma_{\varphi z}(r)&\displaystyle=-\frac{4G\varphi}{\pi}\frac{r}{\sqrt{a^{2}-r^{2}}},\quad r\leq a,\\ \displaystyle u_{\varphi}(r)&\displaystyle=\frac{2}{\pi}\varphi\left[r\arcsin\left(\frac{a}{r}\right)-a\sqrt{1-\frac{a^{2}}{r^{2}}}\right],\quad r> a,\end{aligned}$

(5.2)

where G is the shear modulus. The stresses and displacements are represented in a normalized form in Figs. 5.2 and 5.3. The total torsional moment is:

$M_{z}=\frac{16}{3}Ga^{3}\varphi.$

(5.3)

../images/459405_1_En_5_Chapter/459405_1_En_5_Fig1_HTML.png — Fig. 5.1
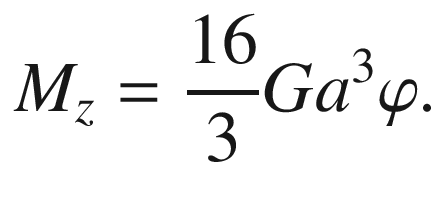
Torsional contact between a rigid flat punch and an elastic half-space

../images/459405_1_En_5_Chapter/459405_1_En_5_Fig2_HTML.png — Fig. 5.2
Normalized torsional stresses as a function of the radial coordinate for torsion by a flat cylindrical punch

../images/459405_1_En_5_Chapter/459405_1_En_5_Fig3_HTML.png — Fig. 5.3
Normalized tangential displacements as a function of the radial coordinate for torsion by a flat cylindrical punch

5.1.2 Displacement from Torsion by a Thin Circular Ring

We will now consider the torsion of the elastic half-space induced by a moment $M_{z}$ that is distributed over a thin circular ring of radius a. Let the ring be sufficiently thin for the stress distribution to be described by a Dirac function:

$\sigma_{\varphi z}(r)=-\frac{M_{z}}{2\pi a^{2}}\delta(r-a).$

(5.4)

The resulting displacement of the half-space can be gained from the superposition of the fundamental solutions of elasticity theory. A point force $F_{x}$ acting in the x-direction on the origin causes the tangential displacements at the half-space surface (Johnson 1985 ) of:

$\begin{aligned}\displaystyle u_{x}&\displaystyle=\frac{F_{x}}{2\pi G}\left[\frac{1}{s}\left(1-\nu\right)+\nu\frac{x^{2}}{s^{3}}\right],\\ \displaystyle u_{y}&\displaystyle=\frac{\nu F_{x}}{2\pi G}\frac{xy}{s^{3}},\end{aligned}$

(5.5)

with s being the distance from the point of the force application. A force in the y-direction results in correspondingly identical expressions for the opposite coordinates. A slightly involved yet elementary calculation yields the displacements caused by the stress distribution (5.4):

$\begin{aligned}\displaystyle u_{\varphi}(r;a)&\displaystyle=\frac{1}{2\pi G}\int_{0}^{2\pi}\frac{M_{z}}{2\pi a}\frac{\cos\varphi\mathrm{d}\varphi}{\sqrt{a^{2}+r^{2}-2ar\cos\varphi}}\\ \displaystyle&\displaystyle=\frac{M_{z}}{2\pi^{2}Ga^{2}}\left[\frac{r^{2}+a^{2}}{r^{2}+ar}\mathrm{K}\left(\frac{2\sqrt{ra}}{r+a}\right)-\frac{(r+a)^{2}}{r^{2}+ar}\mathrm{E}\left(\frac{2\sqrt{ra}}{r+a}\right)\right],\end{aligned}$

(5.6)

with the complete elliptical integrals of the first and second kind:

$\begin{aligned}\displaystyle\mathrm{K}(k)&\displaystyle:=\int_{0}^{\pi/2}\frac{\mathrm{d}\varphi}{\sqrt{1-k^{2}\sin^{2}\varphi}},\\ \displaystyle\mathrm{E}(k)&\displaystyle:=\int_{0}^{\pi/2}\sqrt{1-k^{2}\sin^{2}\varphi}\mathrm{d}\varphi.\end{aligned}$

(5.7)

These displacements are displayed in Fig. 5.4 and allow the direct calculation of the displacements from a given rotationally symmetric torsional stress distribution.

../images/459405_1_En_5_Chapter/459405_1_En_5_Fig4_HTML.png — Fig. 5.4
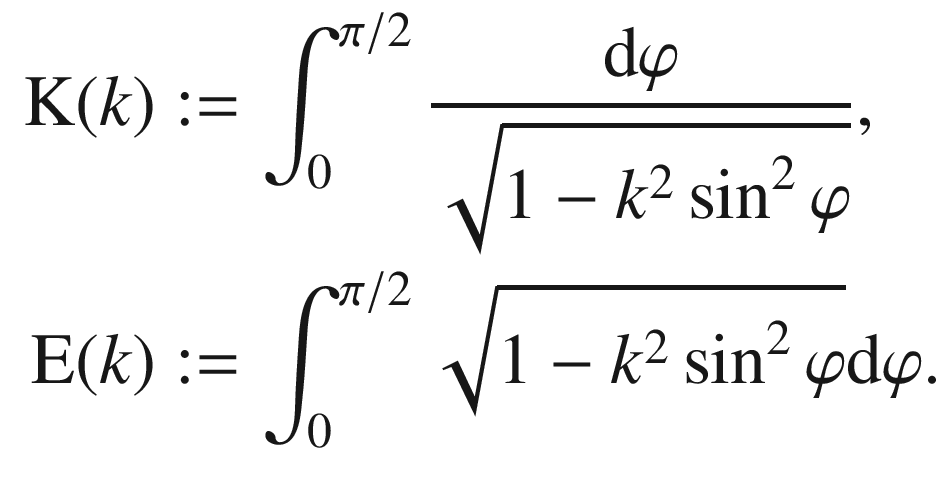
Tangential displacement of the surface from torsion by a thin circular ring

5.2 Contacts with Slip

We now consider contacts which are simultaneously loaded in the z-direction by a normal force $F_{N}$ and a twisting moment $M_{z}$ . Once again, the problem can be reduced to the contact between a rigid indenter and an elastic half-space by introducing the effective modulus of elasticity:

$\frac{1}{E^{*}}=\frac{1-\nu_{1}}{2G_{1}}+\frac{1-\nu_{2}}{2G_{2}}=\frac{1-\nu}{2G},$

(5.8)

with the shear moduli $G_{i}$ and Poisson’s-ratios $\nu_{i}$ . The index “1” denotes the indenter and “2” the half-space. Many statements from Chap. 4 concerning tangential contacts with slip also hold true for torsional contacts with slip: the contacts exhibit hysteresis and memory, i.e., the solution of the contact problem is dependent on the loading history. Once again, we restrict ourselves to contacts with a constant normal force and a subsequently applied, increasing twisting moment. This induces a slip zone of radius a, which gradually expands inwards from the boundary of the contact. The inner stick zone is characterized by the radius c.

Contrary to tangential contacts, there exists no theorem for torsional contacts permitting the reduction to the solution of the frictionless normal contact. Nevertheless, Jäger (1995 ) published a general solution for arbitrary rotationally symmetric indenters with a profile shape $\tilde{z}:=f(r)$ . The boundary conditions for the normal and tangential stresses $\sigma_{zz}$ and $\sigma_{\varphi z}$ as well as the normal and tangential displacements w and $u_{\varphi}$ at the surface of the half-space are:

$\begin{aligned}\displaystyle w(r)&\displaystyle=d-f(r),&\displaystyle&\displaystyle r\leq a,\\ \displaystyle u_{\varphi}(r)&\displaystyle=r\varphi,&\displaystyle&\displaystyle r\leq c,\\ \displaystyle\sigma_{\varphi z}(r)&\displaystyle=\mu\sigma_{zz}(r),&\displaystyle&\displaystyle c<r\leq a,\\ \displaystyle\sigma_{zz}(r)&\displaystyle=0,&\displaystyle&\displaystyle r> a,\\ \displaystyle\sigma_{\varphi z}(r)&\displaystyle=0,&\displaystyle&\displaystyle r> a,\end{aligned}$

(5.9)

with the indentation depth d, the torsion angle ${\varphi}$ , and the coefficient of friction ${\mu}$ . We assume that the pure normal contact problem has been solved and the corresponding normal stresses $\sigma_{zz}$ are known (refer to Chap. 2 for details). The solution of the torsion problem then requires just a single function $\tilde{\phi}$ , which can be determined from the condition:

$\tilde{\phi}(x;a)=-\frac{\mu}{2G}\int_{x}^{a}\sigma_{zz}(r)\frac{\mathrm{d}r}{\sqrt{r^{2}-x^{2}}}.$

(5.10)

The relationship between the torsion angle and the two characteristic contact radii c and a is then given by:

$\varphi=\tilde{\phi}(c;a).$

(5.11)

Moreover, the twisting moment can be calculated from the equation:

$\begin{aligned}\displaystyle M_{z}(c,a)&\displaystyle=16G\left(\varphi\frac{c^{3}}{3}+\int_{c}^{a}x^{2}\tilde{\phi}(x,a)\mathrm{d}x\right)\\ \displaystyle&\displaystyle=16G\varphi\frac{c^{3}}{3}-4\mu\int_{c}^{a}\left[c\sqrt{r^{2}-c^{2}}+r^{2}\arccos\left(\frac{c}{r}\right)\right]\sigma_{zz}(r)\mathrm{d}r,\end{aligned}$

(5.12)

and the torsional stresses in the stick zone are determined by the relationship:

$\sigma_{\varphi z}(r)=-\frac{4Gr}{\pi}\int_{c}^{a}\frac{\mathrm{d}\tilde{\phi}(x,a)}{\mathrm{d}x}\frac{\mathrm{d}x}{\sqrt{x^{2}-r^{2}}},\quad r\leq c.$

(5.13)

The tangential displacements in the slip zone are given by the relationship:

$u_{\varphi}(r)=r\left[\varphi-\frac{4}{\pi r^{2}}\int_{c}^{r}x^{2}\left[\varphi-\tilde{\phi}(x;a)\right]\frac{\mathrm{d}x}{\sqrt{r^{2}-x^{2}}}\right],\quad c<r\leq a.$

(5.14)

Equations (5.10) to (5.14) completely solve the described torsion problem. The problem is fully defined by providing the indenter profile and one quantity of each trio $\{d,a,F_{N}\}$ and $\{\varphi,c,M_{z}\}$ . We assume in both cases that the two radii are the given quantities. Regrettably, these relationships very rarely permit an analytical solution. Therefore, we will limit the scope of detail provided in this book to the indentation by a flat cylindrical punch and by a paraboloid. The following contact problems occur, for example, in stick-slip (purely mechanical) rotary drive systems. There, the most commonly used indenter shape is the sphere (see Sect. 5.2.2).

5.2.1 The Cylindrical Flat Punch

In Chap. 2 (see Sect. 2.5.1) we considered the normal indentation of an elastic half-space to the depth d by a rigid, flat cylindrical indenter of radius a. The following stress distribution was found:

$\sigma_{zz}(r;d)=-\frac{E^{*}d}{\pi\sqrt{a^{2}-r^{2}}},\quad r\leq a.$

(5.15)

Using (5.10) we obtain:

$\tilde{\phi}(x;a)=\frac{\mu E^{*}d}{2\pi G}\int_{x}^{a}\frac{1}{\sqrt{a^{2}-r^{2}}}\frac{\mathrm{d}r}{\sqrt{r^{2}-x^{2}}}=\frac{\mu E^{*}d}{2\pi Ga}\mathrm{K}\left(\sqrt{1-\frac{x^{2}}{a^{2}}}\right),$

(5.16)

with the complete elliptical integral of the first kind:

$\mathrm{K}(k):=\int_{0}^{\pi/2}\frac{\mathrm{d}\varphi}{\sqrt{1-k^{2}\sin^{2}\varphi}}.$

(5.17)

The torsion problem is solved through the following relationships between the global torsion angle ${\varphi}$ , the radius of the stick zone c, and the torsion moment $M_{z}$ as well as the tangential stresses $\sigma_{\varphi z}$ :

$\begin{aligned}\displaystyle\varphi&\displaystyle=\frac{\mu E^{*}d}{2\pi Ga}\mathrm{K}\left(\sqrt{1-\frac{c^{2}}{a^{2}}}\right),\\ \displaystyle M_{z}&\displaystyle=16G\varphi\frac{c^{3}}{3}+\frac{8\mu E^{*}d}{\pi a}\int_{c}^{a}x^{2}\mathrm{K}\left(\sqrt{1-\frac{x^{2}}{a^{2}}}\right)\mathrm{d}x,\\ \displaystyle\sigma_{\varphi z}(r)&\displaystyle=-\frac{4Gr}{\pi}\left[\int_{c}^{a}\frac{\mathrm{d}\tilde{\phi}(x,a)}{\mathrm{d}x}\frac{\mathrm{d}x}{\sqrt{x^{2}-r^{2}}}+\frac{\tilde{\phi}\left(a,a\right)}{\sqrt{a^{2}-r^{2}}}\right],\quad r\leq c\\ \displaystyle&\displaystyle=-\frac{2\mu E^{*}dr}{\pi^{2}a}\\ \displaystyle&\displaystyle\quad{}\cdot\Bigg\{\int_{c}^{a}\left[x\mathrm{K}\left(\sqrt{1-\frac{x^{2}}{a^{2}}}\right)-\frac{a^{2}}{x}\mathrm{E}\left(\sqrt{1-\frac{x^{2}}{a^{2}}}\right)\right]\frac{\mathrm{d}x}{\left(a^{2}-x^{2}\right)\sqrt{x^{2}-r^{2}}}\\ \displaystyle&\displaystyle\qquad{}+\frac{\pi}{2\sqrt{a^{2}-r^{2}}}\Bigg\},\end{aligned}$

(5.18)

with the complete elliptical integral of the second kind:

$\mathrm{E}(k):=\int_{0}^{\pi/2}\sqrt{1-k^{2}\sin^{2}\varphi}\mathrm{d}\varphi.$

(5.19)

For the sake of brevity, the tangential displacements in their general form will not be repeated here as they have already been demonstrated in (5.14). Complete stick in the contact is possible even for a non-vanishing torsion angle and a corresponding torque. The respective limiting values are:

$\begin{aligned}\displaystyle\varphi(c=a)&\displaystyle=\varphi_{c}=\frac{\mu E^{*}d}{4Ga}=\frac{\mu d}{2(1-\nu)a},\\ \displaystyle M_{z}(c=a)&\displaystyle=M_{c}=16G\varphi_{c}\frac{a^{3}}{3}=\frac{4}{3}\mu E^{*}da^{2}=\frac{2}{3}\mu F_{N}a.\end{aligned}$

(5.20)

The torsional moment and torsion angle, both normalized to these critical values, are displayed in Figs. 5.5 and 5.6 as functions of the normalized radius of the stick zone. The variation of the torsion moment during the transition from complete stick to complete slip is less than 18%. The normalized distribution of the torsional stresses is given in Fig. 5.7 and tangential displacements is provided in Fig. 5.8.

../images/459405_1_En_5_Chapter/459405_1_En_5_Fig5_HTML.png — Fig. 5.5
Torsion angle, normalized to the critical value for complete stick, as a function of the normalized radius of the stick zone for the torsional contact with a flat punch

../images/459405_1_En_5_Chapter/459405_1_En_5_Fig6_HTML.png — Fig. 5.6
Torsional moment, normalized to the critical value for complete stick, as a function of the normalized radius of the stick zone for the torsional contact with a flat punch

../images/459405_1_En_5_Chapter/459405_1_En_5_Fig7_HTML.png — Fig. 5.7
Torsional stresses normalized to the average pressure $p_{0}$ multiplied with the coefficient of friction $\mu$ for the torsional contact with a flat cylindrical punch. The thin solid line represents the stress distribution for complete slip

$$p_{0}$$ — Fig. 5.7
Torsional stresses normalized to the average pressure $p_{0}$ multiplied with the coefficient of friction $\mu$ for the torsional contact with a flat cylindrical punch. The thin solid line represents the stress distribution for complete slip

../images/459405_1_En_5_Chapter/459405_1_En_5_Fig8_HTML.png — Fig. 5.8
Normalized tangential displacements for the torsional contact with a flat cylindrical punch. The thin solid line represents the displacement caused by the rigid body rotation

5.2.2 The Paraboloid

In Chap. 2 (see Sect. 2.5.3), for a paraboloid with the curvature radius R and the corresponding profile shape

$f(r)=\frac{r^{2}}{2R},$

(5.21)

the following solution of the normal contact problem was derived:

$\begin{aligned}\displaystyle d(a)&\displaystyle=\frac{a^{2}}{R},\\ \displaystyle F_{N}(a)&\displaystyle=\frac{4}{3}\frac{E^{*}a^{3}}{R},\\ \displaystyle\sigma_{zz}(r;a)&\displaystyle=-\frac{2E^{*}}{\pi R}\sqrt{a^{2}-r^{2}},\quad r\leq a.\end{aligned}$

(5.22)

As usual, a denotes the contact radius, d the indentation depth, $F_{N}$ the normal force, and $\sigma_{zz}$ the normal stress distribution in the contact.

Taking (5.10) into account gives us (for $\tilde{\phi}$ ):

$\tilde{\phi}(x;a)=\frac{\mu E^{*}a}{\pi GR}\left[\mathrm{K}\left(\sqrt{1-\frac{x^{2}}{a^{2}}}\right)-\mathrm{E}\left(\sqrt{1-\frac{x^{2}}{a^{2}}}\right)\right],$

(5.23)

with the complete elliptical integrals of the first and second kind:

(5.24)

The solution for the torsion problem (see Fig. 5.9), initially found by Lubkin (1951 ), is then given by:

$\begin{aligned}\displaystyle\varphi&\displaystyle=\frac{\mu E^{*}a}{\pi GR}\left[\mathrm{K}\left(\sqrt{1-\frac{c^{2}}{a^{2}}}\right)-\mathrm{E}\left(\sqrt{1-\frac{c^{2}}{a^{2}}}\right)\right],\\ \displaystyle M_{z}&\displaystyle=16G\varphi\frac{c^{3}}{3}\\ \displaystyle&\displaystyle\quad{}+\frac{16\mu E^{*}a}{\pi R}\int_{c}^{a}x^{2}\left[\mathrm{K}\left(\sqrt{1-\frac{x^{2}}{a^{2}}}\right)-\mathrm{E}\left(\sqrt{1-\frac{x^{2}}{a^{2}}}\right)\right]\mathrm{d}x,\\ \displaystyle\sigma_{\varphi z}(r)&\displaystyle=-\frac{4\mu E^{*}ar}{\pi^{2}R}\int_{c}^{a}\mathrm{E}\left(\sqrt{1-\frac{x^{2}}{a^{2}}}\right)\frac{\mathrm{d}x}{x\sqrt{x^{2}-r^{2}}},\quad r\leq c.\end{aligned}$

(5.25)

Here, ${\varphi}$ represents the global torsion angle of the rigid paraboloid, $M_{z}$ the torsional moment, and $\sigma_{\varphi z}$ the torsional stresses. The torsion angle and the torsional moment as functions of the radius of the stick zone are represented in a normalized form in Figs. 5.10 and 5.11. Furthermore, Figs. 5.12 and 5.13 display the normalized tangential stresses and displacements as functions of the radial coordinate.

../images/459405_1_En_5_Chapter/459405_1_En_5_Fig9_HTML.png — Fig. 5.9
Torsional contact between a rigid paraboloid and an elastic half-space

../images/459405_1_En_5_Chapter/459405_1_En_5_Fig10_HTML.png — Fig. 5.10
Normalized torsion angle as a function of the normalized radius of the stick zone for the torsional contact with a parabolic indenter

../images/459405_1_En_5_Chapter/459405_1_En_5_Fig11_HTML.png — Fig. 5.11
Normalized torsional moment as a function of the normalized radius of the stick zone for the torsional contact with a parabolic indenter

../images/459405_1_En_5_Chapter/459405_1_En_5_Fig12_HTML.png — Fig. 5.12
Torsional stresses normalized to the average pressure $p_{0}$ multiplied by the coefficient of friction $\mu$ for the torsional contact with a flat cylindrical punch. The thin solid line represents the stress distribution for complete slip

$$p_{0}$$ — Fig. 5.12
Torsional stresses normalized to the average pressure $p_{0}$ multiplied by the coefficient of friction $\mu$ for the torsional contact with a flat cylindrical punch. The thin solid line represents the stress distribution for complete slip

../images/459405_1_En_5_Chapter/459405_1_En_5_Fig13_HTML.png — Fig. 5.13
Normalized tangential displacements for the torsional contact with a parabolic indenter. The thin solid line represents the displacement caused by the rigid body rotation

Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.

The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.