2
Selection in Islam

Among the Christians who equipped themselves with Aristotle’s Organon to dispute about the nature of the Trinity and other enigmas were followers of the patriarch of Constantinople, Nestorius, who was excommunicated in 431 ce. When expelled from the Roman Empire they settled in Persia, at Jundishapur, a town built 200 years earlier to house captive Roman soldiers. There the Nestorians built an important school and hospital in which they enlarged their study of Aristotle and Galen. Vigorous missionaries, the Nestorians became experts in translating difficult texts between unrelated languages. The early Arabian conquests to the east increased the scope of Nestorian missionary activity. The caliphs usually considered them as allies because they had enemies and beliefs in common, and the Qur’ān recognized them as fellow “People of the Book,” provided they paid their taxes.
The first era of Arabian expansion ended in the mid-eighth century. The dynasty that had presided over most of it, the Umayyads, headquartered in Damascus, succumbed to a clan with Persian backing, the Abbasids, who built a new city, Baghdad, as its power base. Nestorian learning found a growing audience in the eclectic urban elite drawn to the new capital from around the conquered lands. In 765 the director of the hospital at Jundishapur became the Abbasids’ court physician. Syriac-speaking Christian doctors soon swarmed in the new capital. They supplied the translators who made Aristotle “The Philosopher” in the Arabic language.
The project to render Greek science into Arabic lasted three centuries. The translators had to invent many new technical terms, even a word for philosophy, for which they adopted the transliteration falsafa. In the early ninth century, the Abbasid Caliph al-Mamūn (813–33) established an academy or research center and library at Baghdad, the House of Wisdom, which gathered works by Greek medical writers and mathematicians as well as Aristotle. By 1050 every Aristotelian treatise except the Politics existed in Arabic, together with many books like the Mechanica incorrectly ascribed to him (see Figure 5).
The wealthy of Baghdad supported this activity, which, during the heyday of the House of Wisdom, centered on a wide competitive search for ancient manuscripts. This unusual treasure hunt had to do with the rapid rise of the Islamic state. Lacking administrative experience, the Arabian conquerors employed the dīwān, or bureaucratic offices and procedures of the Persian Empire, to tax, survey, and keep records. The new empire kept its books in Persian until late Umayyad times when it shifted to Arabic. That required translation of the dīwān manuals, which probably included introductions to arithmetic, geometry, and branches of applied mathematics.
The shift to Arabic opened the bureaucracy to place hunters and, insofar as careers were open to talent, intense competition. Mastery of applied mathematics may have helped people with ambitions of upper-level appointments; hence the hunt for mathematical treatises in depositories in Byzantium and elsewhere. Once domesticated by this process, mixed mathematics became a pursuit in its own right, though still supported for its applications to administration, engineering, and religious observance. Thus, unlike the Greeks, most Muslim physici and mathematicians were courtiers, officials, or functionaries.
The arts of reasoning and persuasion, useful for making headway in Baghdad’s sophisticated philosophical salons and a name in religious controversy, again served as a stalking horse for the rest of Aristotle’s system. The early Abbasids favored a liberal form of kalām (scholastic exegesis of religious writings), Mu’tazila, which allowed wide scope to reason in the interpretation of obscure or implausible passages in Scripture and in the attainment of moral as well as philosophical truth. The Aristotelian corpus showed what reason unaided by revelation could achieve. It also bore directly on such practical matters as astrology and meteorology, and hylomorphism (the doctrine of form and matter) provided the vocabulary for discussion, if not the ingredients for solution, of most questions about everyday experience.
These practical considerations may be taken as the efficient cause of the translations and the commentaries and compendia descended from them. The principles of knowledge, and the ways to wisdom, might be adduced as formal and final causes. There remains the material cause. It was paper. The Arabs became acquainted with this Chinese invention during their conquests in Central Asia. A paper mill operated in Baghdad before 800 to help meet the needs of record keepers. More paper became available just when al-Mamūn’s translators needed it. A large market in books developed, supplied by an assembly line, or rather circle, of scribes who simultaneously took dictation from an author or scholar. The scribes read back what they had taken down and the dictator, if satisfied, “authorized” the copies. The system produced more, and more faithful, versions of the originals than monastic scribes could make one at a time on vellum or parchment. Colossal libraries came into being, the largest, at 400,000 or 500,000 volumes, being over a hundred times the size of their nearest competitors in the West.
Central administration of the new empire proved impossible. As soon as the great expansion peaked in the eighth century its parts began to separate. In the tenth century, caliphates split off in Egypt under a dynasty claiming direct descent from the Prophet’s daughter Fatima, and in Andalusia under a branch of the Ummayads. At the same time, the Abbasids lost all power in the East to Turkish and Persian shahs and emirs. These arrangements proved fleeting: in 1031 the Umayyads lost Andalusia to fundamentalist Muslims from North Africa; in 1171 the Fatimids gave way to the Kurd Saladin; in 1258 the Mongols destroyed Baghdad. Nonetheless, a common language for literature and administration, and conversions to Islam, kept the disparate political elements together as a cultural, religious, and commercial “empire.”
Because of the wide distribution in place and time of niches for its cultivation, falsafa could develop only in fits and starts in Islamic lands. Hence the enormous energy devoted to producing digests, encyclopedias, and commentaries on standard material by the most gifted of the Islamic philosophers, and a reason that they did not develop a physica much different from what they inherited. Another reason is that, in contrast to mathematics, physica had consequences for faith. Aristotle’s Indifferent God, whether pure or, as was largely the case, Neoplatonized, could be Islamized, as he was Christianized, only at the expense of the logical consistency of the system. To insist on pure Aristotle, with his eternal world and perishable soul, invited theological opposition.
Falsafa
The House of Wisdom established in Baghdad by al-Mamūn incorporated the library of his father, Harun al-Rashid, the Caliph of the Thousand and one nights, and an observatory for other nocturnal activities. It also sponsored expeditions to measure the size of the Earth. Like the House’s translation project, its astronomical and geographical observations arose from Greek prompts. Al-Mamūn wanted to check Ptolemy and Eratosthenes for the surer estimate of the size of his empire and the relative positions of the principal places in it. Geography flourished wherever encouraged and, with history, made the largest body of literature in the Islamic languages during the Middle Ages, apart from religion. The great figure of the House of Wisdom was not a geographer, however, but an exemplary polymath, the founder of Arabic Aristotelianism, al-Kindī. He is a good example of the generalization made earlier about the social status of Muslim savants. His father, from Yemen, was governor of Kufa in Iraq, whence al-Kindī made his way to Baghdad. In his version of Aristotle, the visible world consists of the four restless elements, the lazy circulating quintessence, form, matter, substance, and accident, and runs on the four causes. The Unmoved Mover transmits motion, and brings about substantial change, through the rotation of the heavens. This stationary Being is Neoplatonic in holding in its mind the Ideas and Forms of created things and Qur’ānic in knowing the particulars of the physical world it created and the characters and deeds of everyone alive and dead. With this adjustment, al-Kindī’s world picture became the standard model of Aristotelian physica until the twelfth century, when defenders of falsafa in Spain advocated a stricter reading of the Philosopher.
At first the amalgam fared well, especially in the hands of al-Fārābī, the son of a Muslim general. Born in remote Turkestan and schooled by a Nestorian Christian, he arrived in Baghdad to earn the sobriquet of “Second Teacher,” Aristotle being the first, for his presentation of Peripatetic philosophy improved by the insights of Islam. His ideal syllabus, The attainment of happiness, advises the truth seeker to begin with things easiest to understand—numbers and geometrical figures—and proceed gradually toward the material world. The journey leads through optics, astronomy, music, and mechanical principles taken as Archimedean abstractions to physica, the science of the things that make up the world. Proceeding again from the least material to the most, the pursuit of happiness sets out from the heavenly bodies and descends through the four elements to stones and the Earth’s interior.
Having understood the four causes of all the species and actions of the physical world, the inquisitive mind inquires about beings more perfect than nature and natural things, and sublimes to metaphysics. Beginning with the soul and intellect of the rational animal, it discovers the way of human perfection and climbs back up the chain of principles, peeling away the material aspects, ascending through ever more perfect rational creatures to the First Principle, the Being too perfect for description. The fulfilled mind now understands the nature and place of everything in the universe, including the Islamic state: for the caliph relates to his hierarchy of subordinates down to the lowest citizen as the First Principle relates to created beings from the highest intellect to the densest stone.
This clear teaching and the support of the Abbasids did not suffice to establish a new Lyceum in Baghdad. Neither al-Kindī nor al-Fārābī led continuous academic lives in the capital. Al-Mamūn’s effort to impose Mu‘tazila failed and his successors oppressed its representatives. The House of Wisdom almost perished and al-Kindī had to leave. Al-Fārābī retained the support of his caliph, with the unhelpful consequence that they were driven out of Baghdad together. After the Second Teacher died eight years later in Damascus, falsafa moved far into Persia, where in 980 it produced one of its finest flowers, Ibn Sīnā (Avicenna), in Bukhara, in what is now Uzbekistan. Extravagantly precocious, he drifted around Persia in search of knowledge, often serving as a physician to the reigning power. His capacious memory held the entire Qur’ān, and much of Greek medicine, mathematics, and physica, which he poured into an antidote to ignorance and insomnia entitled The cure.
The cure proposes the same project as al-Fārābī’s Attainment of happiness, but arranges the steps in the order of the Aristotelian canon. Thus after the Organon come the basic principles of physica, their applications to the celestial and sublunar realms, the mysteries of motion and the human mind, and then mathematics. The last topic is First Philosophy, culminating in knowledge of the One who operates in the Neoplatonic manner of emanation and delegation. Seeking the unification of all knowledge and practice under one set of principles sanctioned by the Qur’ān’s insistence on the oneness of God, Avicenna took on human activities (prayer, prophecy, politics, law) as well as the natural and supernatural worlds, and the techniques, the logic and mathematics, necessary to study them.
Avicenna’s widely read works ended, or suspended, the productive cultivation of falsafa in the eastern reaches of Islam. That was owing primarily to al-Ghazālī (Algazel), a conscientious theologian well versed in kalām and falsafa. After isolating himself for some years to ponder the relations between reason and revelation, he announced that kalām could resolve nothing important for faith, and that falsafa was inimical to it. He emphasized the particulars in which the Unmoved Mover differed from the God of Islam, and pointed out revealed details missing from falsafa, such as the Last Judgment, the resurrection of souls, and the dissolution of the world. He allowed the practice of kalām where helpful in persuading wavering believers of a rationalistic tendency; but, in general, he thought theology and the Sufism to which he inclined would do better without it. His position had the strength of logic and of a new Seljuk ruler in Baghdad, who favored a stronger orthodoxy than the more relaxed religion of the Abbasid caliphs.
The last stage in Aristotle’s journey through Islam jumped two continents, from Persia to Spain, and over a century, from Avicenna to Ibn Bājja (Avempace), the long-serving vizier of the governor of Granada, and Ibn Rushd (Averroes), one-time cadi, or religious judge, in Seville and Cordoba. Both insisted on a purer Aristotle than al-Kindī’s, although with reservations. The better known of the two, Averroes, made his career as a physician and protégé of the Almohad Caliph Abd al-Mu’min before becoming cadi. His literalist renderings of Aristotle and his opposition to al-Ghazālī’s teachings made him the target of traditionalists worried by the successes of the Christian reconquest of Spain. Eventually a high court in Cordoba condemned his approach.
The problems raised by the schism between astronomy and physics appear to have worried Averroes for most of his philosophical life. As a preliminary to their resolution, he tried to separate Aristotelian cosmology from the Neoplatonic and Islamic accretions it had acquired since the time of al-Kindī. That this mélange had become the default falsafa appears from the fable of “Hai Eb’n Yockdan,” as its hero was named in its English translation. Abandoned on a desert island as an infant, Yockdan had plenty of time to think about nature and his place in it. Step by logical step, he invented a Neoplatonic universe on which, after instruction by a passing holy man, he successfully grafted Islam. Averroes declared war on Yockdans. In perceptive analyses of the Aristotelian corpus that would earn him the title of “The Commentator” in the Latin West, he removed the chain of creating and created beings between the One and the lunar Intelligence, restored the eternal cosmos and the Indifferent Mover, severely criticized both Avicenna and al-Ghazālī, and allowed that Aristotle had possessed as much of the truth as a man can obtain without revelation. One of these truths was that Ptolemaic astronomy perpetrated a sham: it might be good mathematics, but it had nothing to do with the real world. The Commentator thus left the Aristotelian corpus as the Arabs had found it 400 years earlier, so that it might almost be said of the gigantic effort of falsafa what Omar Khayyam said of himself after hearing the saints and doctors dispute: “[I] evermore came out by the same door as in I went.”
The blunting of kalām and discouragement of falsafa coincided with an important change in the Islamic educational system. The Abbasid House of Wisdom, with its library and observatory, and its even grander reproduction in Cairo by the Caliph al-Hakīm around 1000, were the high end of a type reproduced in several places in Iraq and Fatamid Egypt. Most in fact were little more than libraries, though some offered ink and the ubiquitous paper to their readers. Originally given over to the “foreign sciences,” the libraries either died out or converted to cultivating the “Islamic sciences” of law, religious studies, and Arabic philology. They did not constitute an educational system.
In early Islamic times, regular elementary education took place in the mosques. But from the eleventh century, schools founded by traditionalists under a provision (wafq) that allowed the endower of a public institution to retain family control over it after his death took over. Mainly Sunni institutions, these madrasas excluded the foreign sciences that had flourished in the largely Shia, Persian-inspired, libraries. The great conquerors in the East, Hūlagū Khan, Timur, the Seljuks, were great founders of madrasas, which helped to inculcate a standard faith and reduce religious controversy. Teaching relied on staggering feats of memorization, first of the Qur’ān, then of the sayings of the Prophet (hadith) and the foundations of the law (fikh). It is said of one overachiever that he died having dictated only 30,000 folio pages of the texts he knew by heart.
Mixed mathematics
Astronomy
Astronomers arrived at Averroes’ view of Ptolemy’s constructions by a steeper path. They began, as did the philosophers, by mastering the translations prepared by denizens of the Baghdad House of Wisdom. That included checking the parameters transmitted in the Almagest. After eight centuries, shortfalls between Ptolemy’s predictions and observation had become conspicuous. For 150 years or so, until around the year 1000, astronomers working in the Islamic East labored to improve the parameters and the methods by which Ptolemy had deduced them. Thus humankind came to have good values for the inclination of the ecliptic, the position of the Sun’s apogee, the precession of the equinoxes, and other desiderata.
Two social factors underpinned this steady progress. The eccentric astronomer Ibn Yūnus, who served the Fatamids and died faithfully in 1009 on the day he had calculated would be his last, specified one of these factors: “observation of the stars agrees with religious law, for it allows us to know the time of prayers and of the sunrise and sunset that mark the beginning and end of fasting.” Hence Islamic astronomers investigated assiduously topics of only passing interest to Ptolemy, like the duration of dawn and dusk, and conditions for glimpsing the first appearance of the new Moon. Also, astronomy taught the direction to Mecca, the qibla, from any place assigned, when to plant, and how to get from one place to another for commerce, pillage, or pilgrimage. Thus, in contrast to physica, the study of the stars, gently recommended in the Qur’ān (6.97, 10.5, 16.12, 16, 71.15–16), had the support of religious leaders. It also had the support of secular rulers, not only because of its help in imposing religious conformity and in guiding caravans, but also because of its foundational role in astrology. Ibn Yūnus was an expert on the subject and his primary patron, the Fatamid Caliph al-Hakīm, the builder of Cairo’s House of Wisdom, was devoted to it. Ibn Yūnus’s huge zij, or handbook of astronomical information, contains tens of thousands of bits of astronomical-astrological data.
The second social factor in the progress of Arabic astronomy was continuity. Whereas physica convulsed periodically, astronomical observation went on almost continuously, in two different senses. For one, observatories, even if they did not outlast their founders, supported frequent determinations of the positions of the luminaries and planets, whereas Ptolemy had calculated his parameters from very few strategically timed observations. Astronomers designed observational programs to last for an entire circuit of Jupiter (12 years) or, even more optimistically, of Saturn (30 years). The Islamic lands were fruitful in astronomers, zijēs, and monumental instruments. For example, at Rayy, 12 kilometers south of Teheran, al-Khujandī, who died in 1000, built a sunken sextant with a radius of 20 meters made of wood sheathed in copper and graduated to ten minutes of arc. With this giant, paid for by the local Persian strongman, he made exact determinations of the obliquity of the ecliptic and the latitude of the instrument.
By 1050 Ptolemaic astronomy had reached its apogee. Astronomers had corrected its parameters via observations with substantial instruments, invented new ways to deduce the parameters from observations, simplified its mathematics with plane and spherical trigonometry, and replaced the cumbersome ancient notation with “Arabic” (that is, Hindu) numerals. What more was there to do? The approaches of three Persian mathematicians of the mid-eleventh century—al-Bīrūnī, al-Khayyāmī (Omar Khayyam), and Ibn al-Haytham (Alhazen)—will indicate the options available.
Al-Bīrūnī, whose erudition was extraordinary even for a Muslim scholar, suffered in good measure the peripeteias of Islamic savants dependent on courts. During his lifetime the north-east fringe of the territory claimed by the powerless Abbasid caliphs changed hands several times. Born and educated in Khwārazm, he fled civil war to seek patronage in the fragmenting kingdoms around him. He met al-Khujandī, observed at the great Rayy sextant, and found temporary employment with fleeting strongmen, one of whom built him an observatory. After the murder of this Maecenas, al-Bīrūnī continued his astronomical and geographical observations in and around Ghazna (Afghanistan). The powerful Ghaznavid Sultan Mahmud knew so little about astronomy that he rejected as heresy the assertion that in the far north the Sun sometimes does not shine for days. Al-Bīrūnī enlightened him and Mahmud reciprocated by giving al-Bīrūnī the opportunity to become the sage of the age. Following the Ghaznavid armies to the east, he mastered Sanskrit, determined geographical positions, and brought back much miscellaneous Indian lore.
Most of al-Bīrūnī’s writing concerns astronomy, geography, and geodesy. Although Ptolemaic in conception, his astronomy analyzes other views, for example, the possibility that the apparent motion of the stars arises from a rotation of the Earth. He gave an Indian as well as a Greek source for this idea and reported Ptolemy’s objections to it (bodies dropped from a tower would land west of its foot) and the response (all bodies on a rotating Earth would participate in its motion even when falling). As many others would do, al-Bīrūnī accepted Ptolemy’s objection, although an incident he recorded suggests that forces beyond his predilections and the demands of his patrons may have recommended his acceptance of the traditional view. He had shown an instrument for finding the time of prayers to an orthodox legalist. The man decried its use because it bore Byzantine names of the months and so opened an entry for the infidel.
Khayyam also suffered the vicissitudes of the Islamic savant for whom good fortune, “like snow upon the desert’s dusty face,” never lasted long. Born in Khurāsān shortly after the Seljuks conquered the province, he spent his most productive years serving Sultan Malik-Shāh in Isfahan. The sultan and his vizier supported an observatory, where, under Khayyam’s direction, a group of astronomers issued their own zij. He or they also developed a new calendar with a tropical year closer by three parts in ten million to the truth than the Gregorian rule. The idyll ended with the death of Malik-Shāh and the assassination of his vizier. The new regime halted the calendar reform, beggared the observatory, and welcomed the orthodox, who opposed Khayyam’s Avicennan world view and poetical free thinking. The line of astronomy he represented, which sought progress in the next place of decimals and required ongoing dependable financing, thus came to an end in Isfahan.
The third example, Alhazen, took the bold position, later pushed by Averroes, that Ptolemaic astronomy had to be reworked to conform to physical principles. He seems to have been a man of unusual confidence, since he proposed to the Fatamid Caliph al-Hakīm—the patron of Ibn Yūnus—a plan to regulate the flow of the Nile. When the plan failed, Alhazen thought it advisable to feign the insanity that his wild project suggested. He recovered his wits when al-Hakīm died and directed them to optics as well as to the shortcomings of Ptolemy. Insisting that the rules of astrophysics required that every rotation ascribed to celestial objects had to be performed by a material shell or sphere turning with constant velocity around its own center, and that no void could exist in the heavens, Alhazen reified all the deferents and epicycles of mathematical astronomy as so many nested globes and marbles, as portrayed in Ptolemy’s Hypotheses. This produced only a qualitative version of a physical astronomy, as it lacked a replacement for equant motion.
The three directions of astronomy represented by al-Bīrūnī, Khayyam, and Alhazen came together briefly and dramatically in the work of Nasīr al-Dīn al-Tūsī. From a family of Shia jurists, al-Tūsī received a full Islamic education from several masters, including a follower of Avicenna. Political turmoil in his homeland (like Khayyam he came from Khurāsān) discouraged the life of the mind, so al-Tūsī accepted an invitation to work in the fastness of a tough Shia sect that specialized in murder. In the company of these Assassins and their grand master, “the Old Man of the Mountains,” he wrote many important tracts, some on ethics, which they certainly needed, others on logic, philosophy, and mathematics. After a quarter century in his unusual academic setting, al-Tūsī upgraded to the service of a grandson of Genghis Khan, Hūlāgū, who destroyed the Assassins in 1256, conquered Baghdad and terminated the Abbasids in 1258, and established his power from the borders of the Byzantine Empire to the fringes of China.
Though a little rough, Hūlāgū had an interest in astronomy and astrology, and encouraged al-Tūsī to gather up manuscripts before his less learned followers ate them. (Perhaps Hūlāgū owed his civility to the Nestorian Christians, from whom his father had chosen his mother and he his favorite wife.) Hūlāgū erected an observatory for al-Tūsī in the new Ilkhan capital of Marāgha in Azerbaijan. This institution, which Hūlāgū not only paid for (which was to be expected) but also, exceptionally, endowed, attracted several excellent astronomers, boasted a library and a librarian, and housed several large instruments including a mural quadrant and an armillary sphere. One of its first products, the result of 12 years of observation and calculation was, of course, a zij. Al-Tūsī and his collaborators disliked the Ptolemaic models on which they had to base their calculations, and, taking their manifesto from the Aristotelian physica eclipsed since al-Ghazālī’s victory over Avicenna, developed new planetary models. This departure, imitated in the fourteenth century by Ibn al-Shātir of Damascus, a liturgical technician (he kept track of religious time), turned out to be a useful step, when, using the same models, Copernicus took a greater stride.
Physics
With some imagination, a savant can find verses in the Qur’ān (15.16, 16.20, 24.35) that encourage the study of astrology and optical phenomena. The greatest investigator of light during the Islamic Middle Ages was Alhazen. As in his astronomy, so in his optics but to better effect, he attempted to combine Aristotle’s physica with geometrical models. Thus, in contrast to most mathematicians, he ascribed vision to rays from a luminous body entering the eye (intromission) rather that to rays from the eye falling on the body (extramission). He distinguished between primary light (from self-luminous bodies like the Sun, planets, and fire), secondary light (from all points on an opaque or transparent body illuminated by primary light), reflected light, and refracted light. This allowed him to state that the Moon shines by secondary, not reflected, light, which rebounds from a polished body only at the angle of incidence—a mathematical version of Plutarch’s description of the lunar surface.
According to Alhazen, rays proceed rectilinearly in all directions from every point on a body shining by primary or secondary light. How then can all the forms and colors they bring to the eye be received without confusion? He answered that rays striking the surface of the crystalline humor perpendicularly dominate the image. As for reflected and refracted light, he was content to define the directions of their actions by experiment. He confirmed in detail the equality of the angles of incidence (i) and reflection, and gave qualitative rules relating i to the deviation d=i−r suffered in refraction, r being the angle of refraction.
Many mathematicians who wrote on astronomy also wrote on mechanics, notably, in the Baghdad school, al-Khwārizmī, whose name inspired an English common noun (“algorithm”), and Thābit ibn Qurra, a money changer from Harrān who became a master of all the mathematical sciences; and, among the Eastern astronomers, al-Bīrūnī, Khayyam, and Avicenna. They built on Archimedes’ theories of the lever and floating bodies, Aristotle’s concepts of weight and motion, and pseudo-Aristotle’s analysis of simple machines (Mechanica). The essential interest of their work lies in its comparative realism: they endeavored, more successfully than in their astronomy, to unite the physical and the mathematical. Thus they did not neglect the weight of the beam when analyzing the equilibrium of a balance or the operation of a lever; and they invented or perfected a “balance of wisdom” with which to measure the specific gravity of anything submersible in a liquid without provoking a chemical reaction. In the case of two-component alloys, algebraic manipulation of the measurements evinced the percentage of the ingredients and gave a more convenient way of detecting counterfeits than Archimedes’ method of dropping them into his bathtub.
The most detailed account of Islamic statics and hydrodynamics comes in al-Khāzinī’s Book of the balance of wisdom, which includes an extensive table of the specific gravities of metals and minerals made by al-Bīrūnī. Al-Khāzinī, who wrote between 1115 and 1130, was the well-educated Byzantine slave of the treasurer of the Seljuk court at Merv in Khurāsān. He debuted in the normal fashion of court astronomers, with a zij dedicated to the ruler. His main accomplishment was the construction of the most precise of balances, a work inspired in equal measure by duty to his master the treasurer, who worried about counterfeit gems and alloys, and pious curiosity about the Day of Judgment, when, as the Qur’ān frequently advises, our deeds will be weighed to the last scruple. The detailed operation of al-Khāzinī’s balance, which employed five weighing pans and reached an accuracy he estimated as one part in 60,000, is less important to know now than his analysis of the stability of balances suspended from axes above, through, or under the beam’s center of gravity.
Al-Khāzinī’s analysis makes the weight of a body depend on its position in two distinct ways. It is the greater the further it hangs from the axis of rotation, and the less the higher the specific gravity or density of the medium it occupies. Invoking a strict though inappropriate analogy to the “weight” (that is, torque) of a body on a balance arm, which runs from zero on the axis to a maximum at the arm’s end, al-Khāzinī made a body’s weight a maximum at the concave surface of the lunar sphere and zero at the Earth’s center. The concept of “weight according to position” and attendant puzzles such as whether a body has weight in its own milieu, as air in air, still figured prominently in Aristotelian physica when Galileo learned it as a student at the University of Pisa.
That was around 1589, just when astrological doctrine elaborated under the early Abbasids by the Jew Māshā’ Allāh, who had helped to calculate a proper day for the founding of Baghdad, predicted an important alteration in human affairs. His astral history turned on the recondite ideas of grand conjunction and trigon change. A trigon is a group of zodiacal signs 120 degrees apart; a grand conjunction brings together Jupiter and Saturn at 20-year intervals; after 200 years or so, during which these reunions take place within a given trigon, they move over to another, and in so doing cause great disruptions (see Figure 6). Do the transitions physically produce disasters or only announce them? Although the Qur’ān suggests (15.81) and reason confirms that the heavens merely advertise, some astrologers, who identified each trigon with one of the four terrestrial elements, predicted disasters related to the qualities of the element characterizing the receiving trigon. Thus when Jupiter and Saturn first come together in the watery trigon they very probably will cause a flood. The greatest effect of trigon shifts occurs after 800 years when the conjunctions complete a full cycle. Hence Galileo arrived eight centuries after Māshā’ Allāh.
Does astrology work through physical agency and therefore belong to physica, or only give notice of future happenings through signs predictable by astronomy, and thus fall to mathematics? In this guise the old problem of the relations between mathematics and physics acquired the additional complication of whether astrology’s predictions, if correctly interpreted, could be avoided. The Qur’ān, which declares frequently that only God knows the future, hints at a possibility of avoidance (16.12, 27.65, 67.5–9). Avicenna and Averroes appealed to these declarations to convict astrology of futility. But the early adepts, like Māshā’ Allāh, al-Kindī, and Thābit ibn Qurra, who worked the literal star lore of Persia into Islamic astrology, accepted the fatalistic principles and predictions of their art. The strictest advocate was the leading Muslim astrologer Abū Ma’shar, another Persian from Khurāsān, who arrived in Baghdad close to the beginning of the reign of al-Mamūn. He taught that the only way for human souls dwelling beneath the Moon to return to the One in the region of light above the stars is to enlist the help of the deities of the planets and constellations. To win it the soul must learn the characters of the stars by studying how astrological influences act physically on terrestrial substances.
Fig. 6. Astral history. Grand conjunctions occur every 20 years, trigon changes every 200 years, and cycle changes every 800 years, more or less. The solid triangle connects the watery signs, the dashed the airy, the dotted the earthy, and the dot-dashed the fiery.
Further illumination on the question of celestial influence can be found in medical practice. Astrologers associated a zodiacal sign with body parts, thus Aries with the head, Taurus with the neck, the Gemini with the shoulders, down to Pisces and the feet. As anyone can work out by observation of the tides and the menstrual cycle, the Moon has some special influence over fluids. Hence it might cause unwanted interference during medically sanctioned bleeding. To minimize the risk, physicians avoided bleeding from any part of the body associated with the zodiacal sign through which the Moon was passing. This beneficial abstention is more plausibly construed as a response to a risk from a real physical force than to a notice delivered by abstract signs. Hence melathesia, the name of this branch of medical practice, was further evidence of the need to integrate terrestrial physics with the mixed mathematics of the heavens.
Departures
In glaring contrast to the philosophers of Greece, members of the Baghdad House of Wisdom from al-Kindī on, and men of many sciences like al-Bīrūnī, Alhazen, and Avicenna, wrote on technological and engineering subjects. The Islamic states undertook large-scale works—for example, the construction of Baghdad, with its mosques, gardens, and palaces—and large-scale wars, with their demands for weapons and fortifications. The decorations of the buildings and their furnishings incorporated geometrical designs of great beauty and complexity, and the strength of the weapons relied on unique and intricate metallurgical processes. The famous swords made of “Damascene steel” combined beauty with utility. The high-end metal industry nourished by military requirements also supplied parts for advanced engineering projects and scientific instruments. Of these latter, the best known is the planispheric astrolabe, which may stand as the emblem or logo of Islamic science.
The finest astrolabes, which consist of several delicately inscribed brass plates contained in a stubby cylinder, were collectors’ items in their time as well as in ours. They could be adjusted to show in a plane the places of the Sun and stars as they are observed in the stellar sphere. The operator needed only to turn the open-work “rete” until one of its star points, or the Sun’s position on the ecliptic, came above the appropriate circle of altitude or azimuth on the lower plate or “tympan” (see Figure 7). A good astrolabe carries several tympans engraved on both sides for use at different latitudes. The concept of the instrument is Greek, its realization in brass Islamic. The oldest extant example, from Isfahan, dates from the tenth century.
Once set, the astrolabe gives the time of day, the time and direction of sunrise and sunset, and, with additional information, the qibla. It can also serve as a compass for navigation. For these reasons it elegantly met the needs of the religion founded by the merchant Muhammad: it gave the times and orientation of daily prayers, guided pilgrims’ steps, and helped caravans cross the desert. And there is more. The sighting bar rotatable against the circular scales on the back of the instrument can measure the radius of the Earth. Al-Bīrūnī took his astrolabe to the top of a high mountain in India adjacent to a flat plain and measured the angle θ between the vertical and the horizon. Any neophyte in Muslim trigonometry could then work out r from sin θ=r/(r+h), h being the mountain height, which al-Bīrūnī measured by a standard surveying technique (see Figure 8). His result confirmed the value obtained by al-Mamūn’s mathematicians, although “their instruments were more precise, and their labor to obtain it of an extremely exacting and fastidious nature.”

Fig. 7. Computer in brass. An Iranian astrolabe showing the rotatable rete with its star points and, underneath it, a tympan with the fixed reference circles of the observer.
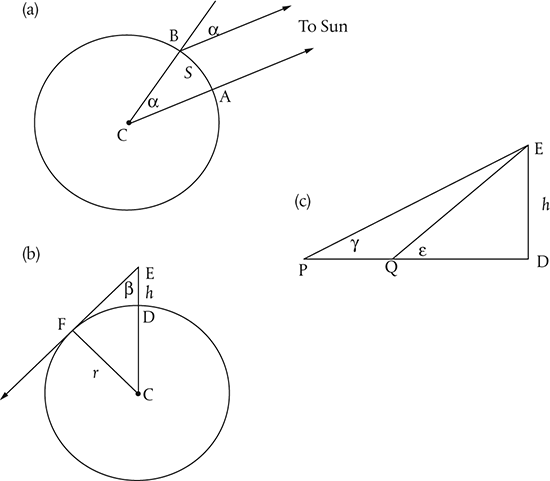
Fig. 8. Size of the Earth. (a) Eratosthenes’ method: A is Aswan, B Alexandria, α the measurable zenith distance of the Sun at B, s the separation of A and B as determined by walking, sailing, or guessing. (b) Al-Birūnī’s method: E is the mountaintop, EF the horizon through F, h the mountain’s height; the rest is trigonometry. (c) h determined from measurements of the angles γ, ε from the stations P and Q and the paced-out distance between them.
We return briefly to the House of Wisdom, where the Banū Mūsā—three sons of a bandit named Mūsā ibn Shākir, who went upmarket to die an astrologer at al-Mamūn’s court—diverted themselves from mathematics to improve the devices of Hero of Alexandria. They added some complicated siphons that, among other feats, appeared to discharge wine and water separately after imbibing them mixed. The greatest mechanician in this tradition worked for a small Turkish dynasty that ruled land around the upper Tigris in the twelfth and thirteenth centuries. He was al-Jazarī, whose Compendium of the theory and practice of the practical arts, “the most important document on machines from ancient times to the renaissance from any cultural area,” describes feedback control and other novel techniques. A fine example of his automatons, the elephant clock, carries an open domed tower with a phoenix on top (see Figure 9). A figure sits on a ledge beneath the dome flanked by falcon heads. Half way down the tower under each falcon a dragon rides on a horizontal axis. A scribe sits at the tower’s base just behind the mahout. The elephant’s body contains a large vessel full of water in which a perforated wooden bucket, loosely attached by ropes to some gearing, floats. Action begins when, in precisely 30 minutes, the leaky bucket sinks, pulling the ropes and engaging the gears, which make the phoenix whirl, causing a ball to fall and the figure on the ledge to decide from which of the falcon heads the ball will drop into a dragon’s mouth. The lucky dragon swallows the ball, swings on its axis, rewinds the ropes, and brings the bucket back to the surface. The clock continues to play every half hour until it has exhausted its balls.

Fig. 9. The magnificent elephant clock. An elaborate automaton built by al-Jazarī that celebrates every half hour, day and night.
Al-Bīrūnī mentions that gears were applied to astrolabes. The earliest surviving example, which is also the earliest extant intact gear train, dates from 1221. Five finely cut gears mounted inside the backplate drive images of the Moon to indicate its place and age. Dots representing the Sun and Moon show their ecliptic longitudes. Nibs on the rete provide a grip for turning the gears. The inclusion of information about the Moon’s zodiacal position made the astrolabe a medical instrument, since it allowed the doctor to discover with a twist whether or not he should cut his patient. If the twist were provided by a falling weight controlled by an escapement, the geared astrolabe would be a mechanical clock. That is exactly what happened in the West in the fourteenth century. Some of these clocks, and many subsequent imitations, still exist, inadvertently advertising, via their astrolabic faces and solar and lunar pointers, the logo and achievements of medieval Muslim science.

Fig. 10. Stoned students. A scene from the arts faculty at the University of Bologna in the thirteenth century, as recorded on a tombstone.