If evolution is so ongoing and everywhere, why do so many things look as if they are stuck in time? The cat and the dog, the milk and the four limbs, they are the same as they ever were. Or, so it seems. Even in technology evolution, which is happening on a much shorter time scale, we see the ossification of form. The pencil, the fork, and the four wheels of the ox cart and the auto have not changed. Why?
The reason is the phenomenon of diminishing returns, which is as much a part of physics as freedom, economies of scale, hierarchy, and evolution. Diminishing returns are observed in freely evolving flow architectures that have become “mature.” At the mature stage in the evolutionary design, the new changes that continue to occur have marginal or imperceptible effect on the broad outlook and performance of the whole flow architecture.
I begin with two illustrations of the meaning and value of this subtle aspect of the physics of evolution and freedom. These examples are from engineering design, although as we reach in conclusion (p. 134) the phenomenon rules all evolution, including social organization.
First, imagine that you have the freedom to shape a tube through which water is pumped to flow. The tube is straight, its length is fixed, but the shape of the tube cross section is free to vary. The opportunity to shape the cross section is the freedom. The possible cross sections are infinite in number: slits, wedge shapes, trapezoidal shapes, curvilinear polygons, and many more.
As you morph the shape in your imagination, you make a first discovery: the sharp corners of the cross section are bad features. They pinch the flow and act as concentrators of fluid friction. Corners that are more open are beneficial features. You arrive face to face with the secret: the possible designs are infinite; however, in this mountain are hidden a smaller number of cross-sectional shapes that stand above the rest. These are the cross sections shaped as regular polygons.
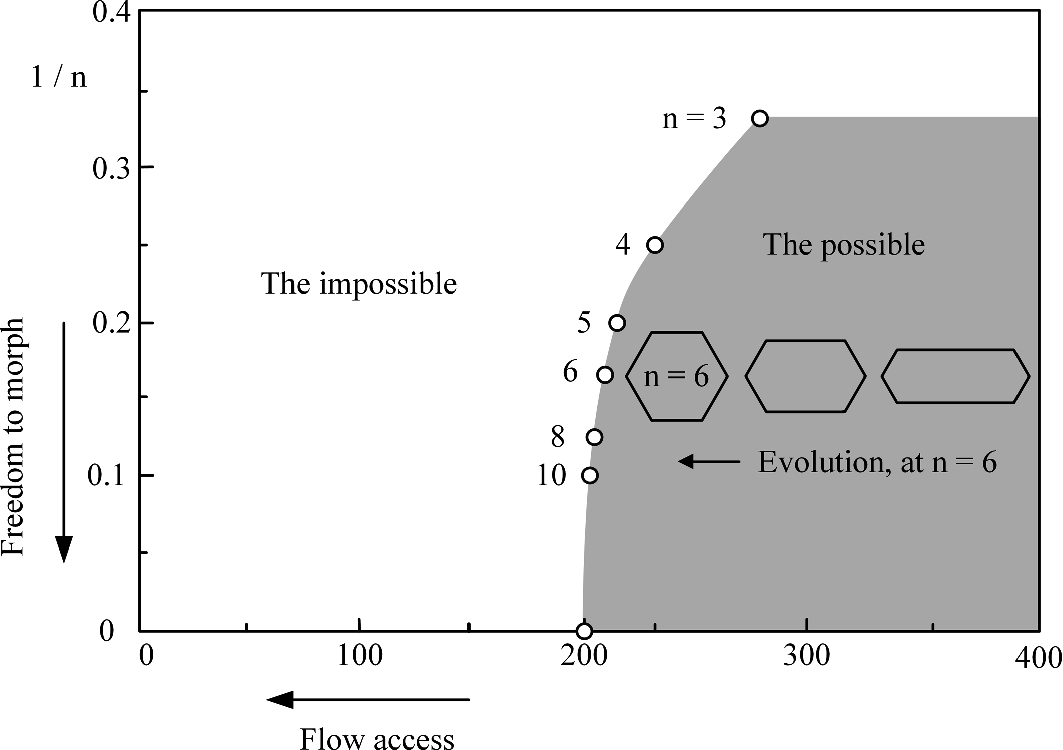
The possible duct flow designs (right) and the impossible designs (left): how the flow through a duct finds easier access by means of greater freedom in morphing its design
The numbers scribed on the abscissa are proportional to the pumping power required to push the water flow through the tube. The same numbers are also proportional to the pressure drop along the tube, the overall flow resistance posed by the tube, and the power destroyed while maintaining the flow. These details are available in Refs. [2, 5]. Here, important is the arrow that points to the left on the abscissa: easier flow access is available to the left, where the abscissa numbers are smaller.
Viewed from above, Fig. 10.1 presents a bird’s-eye view of the movie of evolutionary design. The design must evolve toward the lower left corner. The rectangular frame represents the “design space,” or the territory populated by diverse designs. As you search for easier access, your mind’s images migrate toward the lower left corner. How, by injecting more freedom (n) in the image, unwittingly.
The secret is now in plain view. The few shapes that first came to mind are the regular polygons that do not have unusually tight corners: they form a string of points in Fig. 10.1. With more freedom, these pearls offer greater access. With infinite freedom (
, or 1/n → 0), the flow cross section would offer maximum flow access, except that this shape is relevant as a theoretical limit, as a direction to the evolutionary changes that happen. The purely mathematical circle is not a physical flow cross section in nature or in ducts made by humans, because of imperfections and the unpredictability of the surroundings. In any case, the pearls are ordered on the string the way that makes sense to everybody. The round tube is better than other tube shapes.
Better does not mean much better. Diminishing returns is the phenomenon that rules. The flow access offered by a hexagonal or square cross section is not much worse than the access through a circular cross section. The entire string is populated by winners. Yet, they all look different. They are diverse, but their performance is nearly the same. They are like the winners in the 100 m sprint, who every year climb on the podium with different faces, names, and flags. That’s diversity. The faces are different, but the speed record is essentially the same. That’s diminishing returns.
Diversity is natural, ubiquitous, and the reason why the trivial view of nature is that it is complicated and random. The subtle is the orientation of the string in Fig. 10.1, and the direction toward more freedom, which the string indicates.
The subtle becomes a loud a-ha! when we recognize that the string divides the design space into two worlds—to the right the possible, to the left the impossible. The possible is easy to imagine if we read the figure from right to left at constant n, for example, at n = 6. Constant n means cross-sectional shapes that are polygons with six sides. The point on the string represents the regular hexagon. To the right, on the same n = 6 line, are all the imaginable cross-sectional shapes with six sides that are unequal. None of those shapes perform as well as the regular hexagon. From the n = 6 population, the regular hexagon is the winner.
The impossible is unmasked by continuing to read Fig. 10.1 to the left, at constant n. No drawing can exist to the left of the regular hexagon. Looking for design to the left of the string is like looking for a flowing river basin inside a brick. You are powerful because you know where not to waste your time digging. The string of pearls that marks the limit of the possible is the secret of the impossible.
The possible point-circle flow designs versus the impossible: how the vasculature finds easier flow access because of greater freedom in morphing its configuration
Important is that every possible design is represented by one point in the rectangular frame of freedom versus access. Note that Fig. 10.2 is the same frame as in Fig. 10.1, which is why this second example reinforces the conclusions drawn from the first. On the abscissa, the flow access between the center point and the perimeter increases toward the left. The numbers scribed on the abscissa are proportional to the pumping power and the resistance to flow between center and perimeter.
The freedom to construct the vasculature is measured in terms of the complexity of the drawing, which in Fig. 10.2 increases downward on the ordinate. Again, freedom is measurable. You can count the number of degrees of freedom that one has in making the drawing. The numbers indicate the value of n0, which is the number of tubes that issue from the center. This number decreases when the number of branching levels (or pairing levels, p) increases at constant N. For example, the drawing in the lower left corner has six branching levels, starting with the three tubes coming out of the center, such that the number of points of the circle is N = n02p, namely, 
.
The possible designs are infinite in number. A child can draw something to connect the center of a disc with N points on the perimeter. More clever but equally arbitrary is the so-called “fractal” design labeled “a” and pictured at the same level with “c”, on the horizontal line p = 4. Fractal design is a misnomer. It should be called “postulated (assumed) tree-like.” This design is easy to draw by assuming that the length of each branch is a certain (fixed) fraction of the length of its mother tube. The constancy of the assumed branch/mother ratio of lengths is evident in the design displayed to the right of point “a”.
Most difficult is to let all the tube lengths vary freely, and to conduct the minutious search for an architecture that offers progressively greatest flow access when N and p are specified. Three such drawings are presented in Fig. 10.2. In total, seven of these designs are represented, from p = 6 in the lower left corner, to p = 0 in the upper right corner. The p = 0 design has no branchings, just 192 tubes placed radially from the center to the perimeter. The p = 6 design has the most freedom to morph (the most numerous features to draw) and, as a consequence, it offers the easiest point-circle flow access.
All the possible designs fall to the right of the maximum freedom designs such as points “d”, “c”, and “b”. The hand-picked design “a” falls well to the right of “c”. We conclude that the exhaustive search for morphing the vasculature for progressively greater access ends up dividing the freedom-access space into two design domains. To the right of the winners indicated as points p = 6, 5, 4… is the domain of the possible. To the left is the domain of the impossible. The frontier between the two is the narrow group of designs that are most valuable.
The similarities between Figs. 10.1 and 10.2 are striking. In both figures, the frontier between the possible and the impossible has the same shape. The frontier is not a continuous curve: it is an imagined curve drawn through the few points that represent the winners. The curvature of the curve indicates that “diminishing returns” become reality as the freedom and the complexity of the design increase. The performance of design p = 6 (point “d”) is not much better than the performance of design p = 5. We reached a similar conclusion in Fig. 10.1, after comparing the hexagonal tube (n = 6) with the circular tube (
).
Diminishing returns is a universal phenomenon that accompanies evolution. The more mature the evolving flow configuration, the smaller the improvements in its overall flow-access performance. When the evolving “animal” is old enough the improvements are imperceptible, to the point that the observer believes that evolution has ended. The observer is mistaken. Evolution does not end, it just waits to be kick-started by its unruly environment into a new direction.
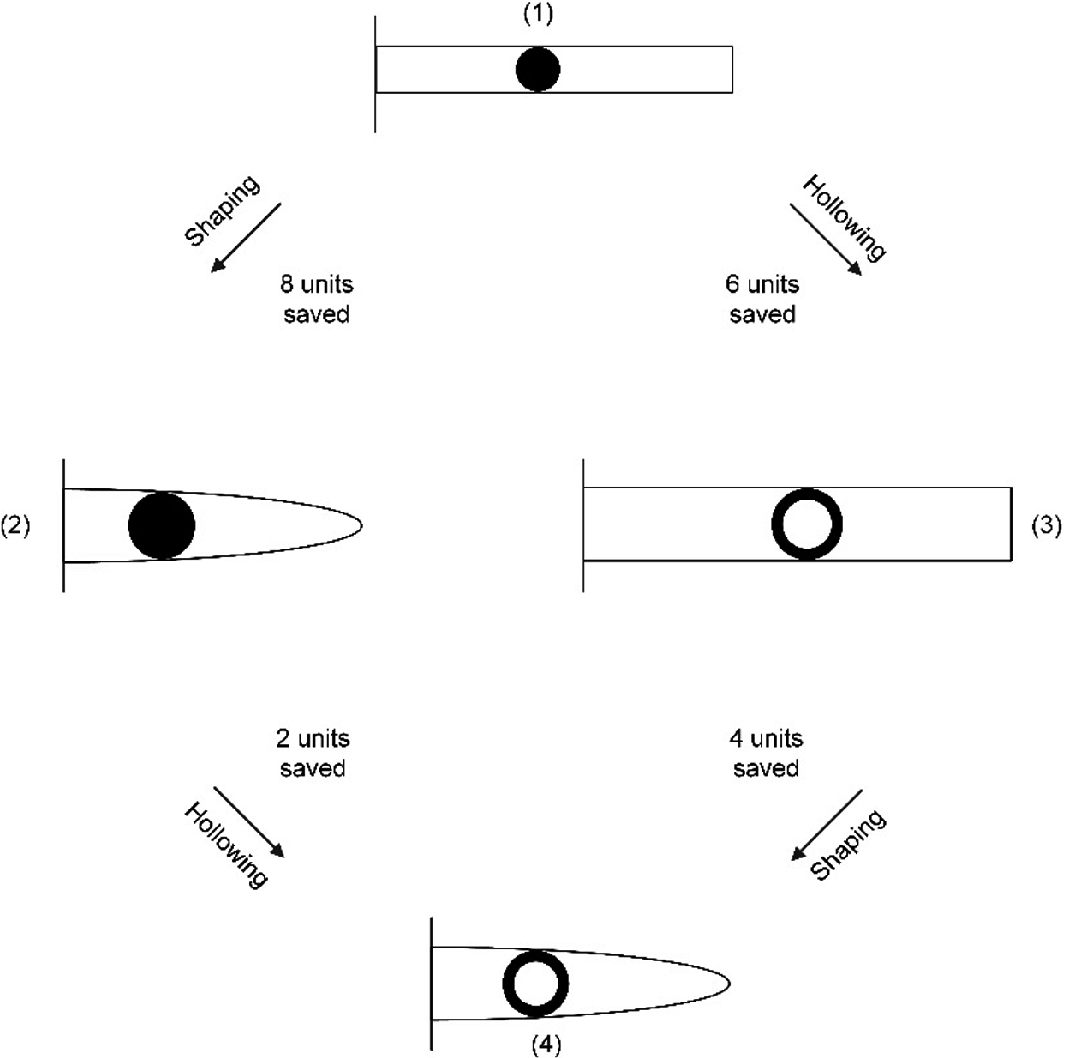
Shaping and hollowing: two directions in the evolution of an elastic cantilever beam with freedom to morph. The load P is attached at the free end, and it points downward. The downward deflection of the free end (δ) is proportional to P
The cantilever beam is an artifact, one of the earliest contrivances inherited from before antiquity. The following description uses the language of mechanics, although the subject applies equally to the evolutionary design of the limbs of trees and the bones of animals [1, 3].
First, the beam happens because it has purpose. The beam improves the life, movement, and survivability of the greater system that adopts it. The greater system is the living human and the life of the whole society, in motion. In Fig. 10.3, the purpose of the beam is to support the end load without breaking and without bending too much. Resistance to breaking means that the internal stresses must not exceed a maximum allowable stress level (sma), which is a property of the beam material. Next, not bending too much means that the beam must have a certain stiffness, which is accounted for by a specified downward deflection of its tip, δ. The cantilever beam is essentially an elastic spring, a blade with a specified spring constant equal to P/δ. The greater the ratio P/δ, the stiffer the beam.
Imagine one of the simplest beam designs, the solid rod with round cross section shown as design (1) in Fig. 10.3. The analysis of a beam with specified P, δ, sma, and E (Young’s modulus of elasticity) is relatively simple and known as slender-beam pure bending theory [2]. We can skip these details and retain the measure of the overall performance of design (1), which is the size of the beam, i.e., the amount of material that one must purchase and use to construct the beam. It turns out that the required volume of material is V1 = 12 units, where the volume unit is the value of the group 
, which is a specified constant because its four factors are specified.
Evolution begins as we search for designs that serve the same need (P, δ) while requiring less material. Such designs are accessible through a series of changes in beam morphology, each change having the effect of removing from the beam some material that is not stressed as highly as the highest stressed regions inside the beam. In design (1), the highest stresses occur in the two armpits at the wall, the dorsal (the back, in tension) and the ventral (the belly, in compression). The lowest stresses (zero, in fact) occur at the free end and along the centerline of the solid rod.
- 1.
Shaping the beam by removing material from near the tip. This way the beam becomes tapered, thick at the base, and thin at the free end, like all tree branches.
- 2.
Hollowing the beam, so that the solid rod is replaced by a tube, like the bone of a bird.
Next come the interesting results, which reveal quantitatively the diminishing returns phenomenon. We imagine three future designs, in this sequence:
If “shaping” is the only direction to morph the design then the resulting design is the tapered solid rod (2), for which the required volume is V2 = 4 units. This represents dramatic savings of material, measured as 8 units of material saved relative to design (1).
If “hollowing” is the only way to change the design then the beam is a hollow tube with the volume V3 = 6 units. The savings of material amount to 6 units, which are also dramatic.
Designs (2) and (3) are the “pioneering” designs, the first announcements of the invention that material can be saved by morphing the beam. Later, as the design matures the design evolution starts from either (2) or (3):
If the shaped design (2) is already available, then it is ripe to be subjected to hollowing. The next result then is a tapered beam that is also hollow, like the top of the original bic pen, or like the root of the goose feather. This is design (4), and its volume requirement is V4 = 2 units. The change from V2 to V4 represents material savings amounting to only 2 units. Notice the diminishing returns that come when the design tends to maturity.
If, on the other hand, the hollowed design (3) is available for the restart of evolution, then it can be subjected to shaping. The resulting design is once again design (4), the hollow tapered beam, which represents the application of “shaping” and “hollowing” together. The change from V3 to V4 brings about material savings amounting to only 4 units.
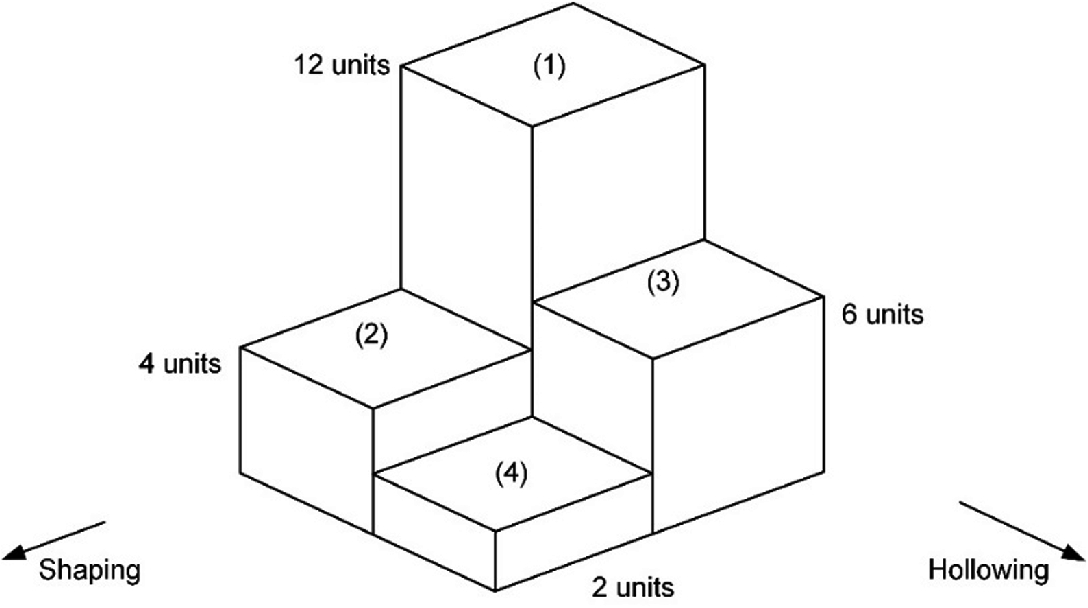
Diminishing returns: the biggest savings in beam material occur early, when each design change is implemented for the first time, alone
The biggest returns are the earliest, 8 units to the left and 6 units to the right, when the object (the beam) was untouched, and each of the design-change ideas was implemented alone. When the evolving design has become more mature, the returns are significantly smaller, 4 units and 2 units, respectively. Smaller steps happen when the two ideas are implemented together.
Diminishing returns become the norm as the design evolves by acquiring more and more design changes that proved to be beneficial in the past, when they were invented and implemented alone. They brought the greatest returns when they were new and not contaminated with similar ideas.
Diminishing returns are everywhere, most visibly in the human sphere, in the evolution of performance, in the shapes of boats, cars and airplanes, and the evolution of records in sports.
For example, ask why speed records are broken more frequently in swimming than in running [6]. The reason is that running is the “mature” design of human locomotion. We are born to walk and run—we are terrestrials. For modern humans, swimming is a young form of locomotion, something to be relearned after the prehistoric aquatic phase of human evolution (p. 119). Each swimmer must learn how to swim, to increase his or her access to movement on the globe, to avoid being stuck on one side of the river, and to gain access to the other side, which is greener. Running on soft sand and snow also requires learning.
Experts on one thing or another will surely jump in with other explanations for the difference between the frequency of records in swimming and the frequency of records being broken in running. They might mention the changes in equipment (suits, shaved body, pool depth, water quality). This argument is correct, and it reinforces the explanation given in the preceding paragraph. The equipment technology for swimming is young and the equipment technology for running is mature. The equipment and the rules of the sport are more likely to change in swimming than in running. The swimming pool is more likely to be improved than the track.
Reheating the high-pressure steam flowing through the turbines of a power plant, and preheating with bled steam the liquid water before it is fed into the boiler
The secret to inventing a more efficient power plant is to morph the circuit executed by its working fluid (e.g., steam) such that it is at a higher temperature when being heated and at a lower temperature when being cooled. The more efficient design is the one that occupies a wider temperature gap between the heat source and the heat sink.
Two methods of widening this temperature gap are shown in Fig. 10.5. The stream of high temperature and high-pressure steam arrives from the left (from the boiler and a subsequent heat exchanger in the same fire house, called superheater) and flows through turbines that generate power. The steam expands, its pressure decreases, and so does its temperature. The design change consists of intercepting the stream halfway through the turbine, and heating it in a special heat exchanger called reheater, which is also exposed to the fire. This way the turbine becomes segmented into two turbines, one for high-pressure steam and the other for low-pressure steam, and the temperature of the steam (averaged over the two turbines) is higher than what it was before the reheater was invented.
Downstream of the low-pressure turbine the steam is condensed into liquid water in a heat exchanger (called condenser) exposed to the cold ambient. Next, the liquid flows through a pump, which increases the water pressure to the high level required for boiling water at a high temperature when exposed to the fire.
The lower part of the drawing in Fig. 10.5 shows another design change, which is for preheating the pressurized water stream arriving from the pump and flowing into the boiler. The smart way to heat the water fed to the boiler (called feedwater) is by placing the water in contact with steam bled from the turbines. This heating invention is valuable because it avoids the mistake of placing the cold water from the pump in direct contact with the fire. Heat transfer across huge temperature differences is a killer of efficiency. The thermodynamics term for this mistake is irreversibility or entropy generation. Again, technical terms and details can be skipped, and can be found in the literature [4].
Important is that in Fig. 10.5 there are two very good inventions, one is reheating and the other is feedwater heating. If implemented, each invention causes an increase in the efficiency of the whole power plant. The efficiency η is the ratio of the shaft power delivered by the turbines divided by the rate of heating (or the rate of fuel consumption) administered to the steam before expansion through the turbines.
Although both reheating and feed heating lead to improvements in the efficiency of the steam turbine cycle, the efficiency increase caused by one method is greater when the method is implemented for the first time, alone. Note the distinction between efficiency (η) and the efficiency increment (Δη) resulting from one or more design changes. The efficiency is the highest when reheating and feed heating are used at the same time.
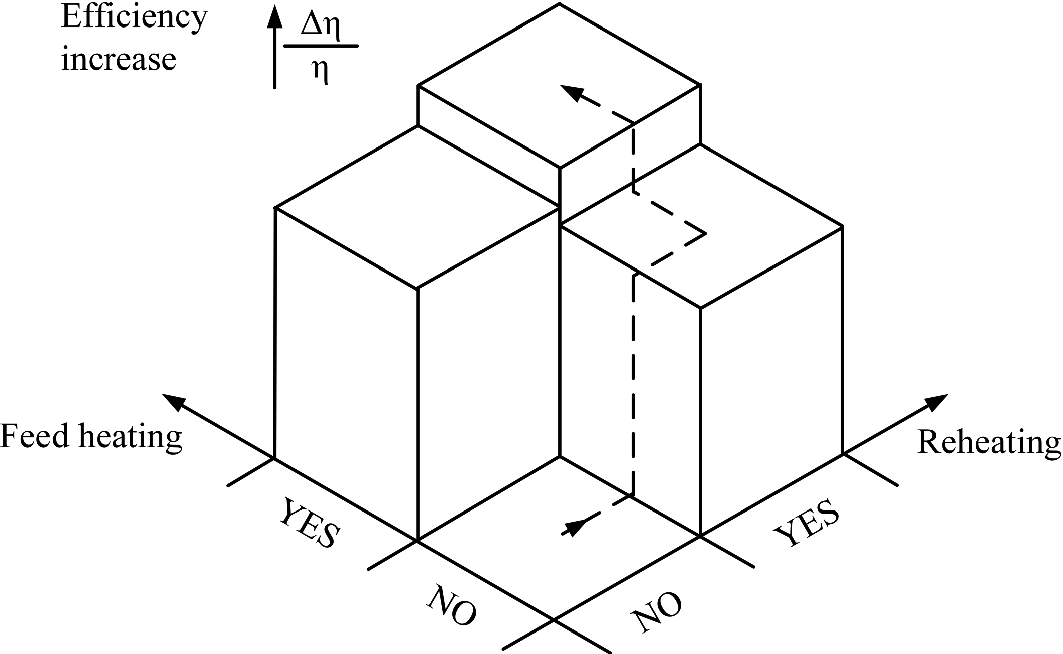
Two design changes that lead to higher global efficiency: reheating and feed heating. The efficiency increase is most pronounced when each change is implemented alone. The increase is smaller when the two inventions are implemented together. Review the same message in Fig. 10.4
There is a lot more to what I selected here for illustration. For example, the number of feed heaters (n, Fig. 10.5) is free to vary. Each feed heater is a flow system with its own flow architecture that can be morphed freely toward better performance, i.e., greater efficiency at the whole system level [4]. It turns out that the design with only one feed heater causes an efficiency increase of 9%, whereas the design with an infinite number of feed-heating stages causes an increase of 20.7%. In other words, the fresh invention (a single feed heater) delivers half of the benefits offered by the most mature and perfected version of the invention (continuous feed heating, or n = ∞).
It’s never like the first time. Returns are like squeezing a lemon. The biggest squirt comes when you squeeze it the first time.
“Gilding the lily” is an apt metaphor for the evolutionary phenomenon that has become mature. Where there is freedom, evolution happens and along with diminishing returns in global performance it gives birth to diversity and complexity. This is, in a nutshell, the visual message of Figs. 10.1, 10.2, 10.3, 10.4, 10.5 and 10.6 and the physics that underpins them. Gilding the lily is most of what goes on in a mature science. It is a good thing, but only up to a point that announces its presence naturally, and when it does it changes the movie plot.
Highlights in the evolution of the second law efficiencies of steam power plants during their history. The data that mark the crest of the domain of possible designs are from Ref. [4]. Note the logarithmic scale on the ordinate, and the ηII = 1 ceiling that no design can surpass. At every point in time, the crest divides the designs into the possible and the impossible, cf., Figs. 10.1 and 10.2
The crest is marked by pioneering designs that at the time were the most efficient. In other words, the shaded body of the mountain accounts for the multitude of designs that are less efficient than the designs that define the crest. On the ordinate, ηII is the second law efficiency of each design, which is a number that cannot be greater than 1. The second law efficiency is the ratio of the power output of the design divided by the corresponding power output of an ideal design (known as reversible engine, or Carnot engine). The crest of the mountain cannot push through the ceiling represented by ηII = 1. Consequently, the crest must be concave, and the concavity in this figure is an illustration of the phenomenon of diminishing returns in the evolution of mature flow architectures.
The subtle aspect that this science illuminates is what is impossible. This is what unites the examples shown here in Figs. 10.1, 10.2, 10.3, 10.4, 10.5, 10.6 and 10.7. This knowledge is very valuable. If we know it we do not waste our time touching and feeling our way over the cliff. This way we avoid the big mistakes. All science is about finding the limit between the possible and the impossible, and how to push the limit, if possible.
This conclusion applies broadly and reaches back to the physics of social organization, with which this book began. The unending evolutionary design of society is better known as politics—the proposals, commands, and implementations of changes in the regulations to human flow on the earth’s surface such as the polis (the city, in Greek). Changes happen, all the time. Some changes are big, while many are small. Some are sudden, cataclysmic, while most are tiny, slow, and imperceptible. Changes happen because every one of us has the urge to change something. Humans cover the range from the complacent to the revolted, with the many dissatisfied in between.
Otto von Bismarck famously said “Politics is the art of the possible.” This wisdom is old, shared broadly and known by other names, such as realism, compromise, trade-off, flexibility, perfection is the enemy of performance, can’t win them all, and the benefit of changing one’s mind. More powerful and useful is to have this wisdom put on a scientific basis. Why, because “the possible” is essentially an infinity of possibilities. With freedom, the social flow architecture can be changed in all sorts of ways, minor and major, related to each other or not related. When it comes to the possible, the sky is the limit. If there is freedom, anything goes…until the morphing design hits the wall between the possible and the impossible. Without freedom, the design is stuck much sooner far to the right in Figs. 10.1, 10.2, and 10.7, far from the better ideas that would be accessible if freedom to question were encouraged.
The way forward is to become better educated about the impossible and to implement what is possible and free, economical, safe, robust, resilient, and long lasting. With science, every new generation is brought up with a greater ability to construct and predict its own future.
True is also that every new generation arrives soaked in unpredictability. Individuals and ideas cannot be predicted. They are like the eddies that rotate “the wrong way” on the surface of the flowing Danube. To focus on the individual is to be blind to the whole. The evolving flow design that serves all the eddies is the river basin, the whole. This is why the future of the whole is the important picture to paint. The better the science, the more clairvoyant and far seeing the painter.