© Springer International Publishing AG 2018
Abdelazim M. Negm (ed.)Groundwater in the Nile Delta The Handbook of Environmental Chemistry73https://doi.org/10.1007/698_2017_210

Resistivity Characterization of Aquifer in Coastal Semiarid Areas: An Approach for Hydrogeological Evaluation

Mohamed Attwa1   and Halim Ali2
(1)
Geology Department, Faculty of Science, Zagazig University, Zagazig, Egypt
(2)
National Authority of Remote Sensing and Space Sciences (NARSS), Cairo, Egypt
 
 
Mohamed Attwa
Email: attwa_m2@yahoo.com
1 Introduction
2 DC/IP Resistivity Methods
2.1 Fundamentals
2.2 Physical Base
2.3 Electrode Arrays and Field Techniques
2.4 Hydraulic Conductivity Prediction
2.5 Geoelectrical Data Inversion
3 Applications to the Nile Delta
4 Conclusions and Recommendations
References

Abstract

In coastal and semiarid regions, the scientific interest lies in imaging the saltwater intrusion and delineating freshwater aquifer zones, respectively. Direct current resistivity (DCR) and induced polarization (IP) geophysical methods are commonly used to assess hydraulic characteristics of the aquifer. Particularly, the main reason for hydrogeophysical application of both DCR and IP is that the electrical characteristics of aquifers depend mainly on the geometry of the pore space and the porosity controlling the soil and rock effective transport properties. For preliminary hydrogeological investigations, these methods are applied at a wide range of field and laboratory scales. Accordingly, the vulnerable zone to the saltwater intrusion and/or contamination can be characterized by high accuracy. Furthermore, empirical and semiempirical relationships are widely used to predict the aquifer petrophysical characteristics, e.g., hydraulic conductivity, using the inversion results of such electrical methods. Equally, conventional and nonconventional DCR inversion algorithms are developed to reduce the nonuniqueness problem of actual resistivity interpretation and, consequently, to obtain more meaningful models than previously reported. As case histories, this chapter demonstrates the efficiency of DCR method for hydrogeological assessment in Nile Delta, Egypt, emphasizing on technical constraints to achieve sustainable development in coastal and semiarid areas.

Keywords

DC inversionDC resistivityHydraulic conductivityHydrogeophysics

1 Introduction

Geoelectrical methods are increasingly popular in detecting and characterizing aquifers as the resistivity of sediments and rocks depends mainly on their water and material contents (e.g., [1–3]). One of such electrical methods is direct current resistivity (DCR) technique. In DCR method, the potential difference is measured via injecting DC into the ground with electrodes at the ground surface. The DCR method has received a great attention because of its potential applications in the field of hydrogeology and saltwater intrusion tomography [4, 5]. In the arid and semiarid region, the DCR method is popularly used for groundwater exploration and aquifer mapping (e.g., [6, 7]). This can be attributed to the rapid advancement in the development of digital modeling solutions and electronic technology of hydrogeological problems (e.g., [8]). Besides the efficiency of such method for lithological characterization, the DCR technique has led to many studies on hydrogeological parameter estimation of the aquifer (e.g., [9]). On the other hand, in the coastal areas, the DCR imaging is suitable for monitoring saltwater intrusion and groundwater contamination as this method quickly investigates a large site without needing for well drilling (e.g., [10]).

Induced polarization (IP) technique is one of the geoelectrical methods based on studying the low-frequency polarization processes taking place in porous media. Generally, the IP method extends from the classical DCR method. Basically, IP measures the earth’s capacity to store an electric charge over time. Accordingly, after the injected current is shut off, the voltage decay curve is measured; the higher the IP, the longer over time the stored charge. It is well known that IP is a considerable and useful method for mineral exploration. On the other hand, the real and imaginary parts of conductivity are measured over a range of frequencies in spectral induced polarization (SIP). The resistivity amplitude and the phase shift between the input current and measured voltage can be recasted into a complex conductivity. Recently, the SIP method has shown its potential to predict the petrophysical parameters in saturated conditions at the field and laboratory scales (e.g., [11, 12]). Usually, DCR method is the preferred, but the resistivity data interpretation suffers from a major flaw: the inability to discriminate between surface and bulk conductivity. This causes unrealistic interpretation in hydrogeophysics. Such main problem can be resolved by using SIP method (e.g., [11, 13, 14]).

In Egypt, the River Nile is the lifeline, where the main water source is surface water from the River. With increasing populations, urbanizations and land reclamation projects in Egypt, the surface water from the River Nile is not sufficient. The groundwater is the second important water resources. Furthermore, the saltwater has intruded from the northern and eastern parts of Egypt along the Mediterranean Sea and Suez Canal, respectively. Additionally, the overpumping of groundwater at the northern parts causes vertical upwelling of saltwater from deeper parts causing degradation to groundwater quality. It can also be noticed that a large part of agricultural areas in the northern parts has been, consequently, affected by saltwater intrusion. Accordingly, the groundwater assessment and management have become extremely important.

This chapter attempts to guide the reader to some of the important sources of information on the use of DCR and IP methods for groundwater assessment. In the first section of this chapter, fundamental of DCR and IP methods will be explained. The linkage between the data of geoelectrical and hydraulic characteristics at the field and laboratory scales will be discussed. The geoelectrical data inversion techniques will be briefly covered in the second section of this chapter. Practically, three cases studied from Nile Delta are presented in the third part. Here, a saltwater intrusion and groundwater resource characterization, i.e., hydrogeophysical characterization, in coastal and semiarid areas, respectively, are reported.

2 DC/IP Resistivity Methods

2.1 Fundamentals

Basically, DCR investigations are based on the principle of applying electric current to the earth through two electrodes and measuring the potential difference between two or more other electrodes. The distance between the electrodes and the measured potential difference is used to make interpretations of subsurface conditions. The geological formation resistivity is a physical property depending on the electric current flow in the formation. Subsurface layers resistivity is controlled by several geological parameters such as rock texture, mineralization, and fluid conductivity contained within the rock. In general, the resistivity increases with grain size and also when the rock is fine-grained and compact. Other factors that affected the rock resistivity include clay content, groundwater salinity, cation exchange capacity, pore water temperature, dissolved salt concentrations, and contaminants (e.g., [15]). Accordingly, the resistivity surveys are the best suited for clay or saline zone delineation. Table 1 shows the resistivity value range of common rocks, soils, and chemicals (e.g., [16]). The soils and sedimentary rocks have a wide variation according to their resistivity. The unconsolidated sediments have lower resistivity values than rocks.
Table 1

Resistivity values of common earth’s materials and chemicals [16]

Materials

Resistivity (Ω m)

Igneous and metamorphic rocks

Granite

5 × 103–106

Basalt

103–106

Marble

102–2.5 × 108

Quartzite

102–2 × 108

Sedimentary rocks

Sandstone

8–4 × 103

Shale

20–2 × 103

Limestone

50–4 × 102

Soils and water

Clay

1–100

Alluvium

10–800

Groundwater (fresh)

10–100

Saltwater

<1

The rock conduction is by way of pore fluids, i.e., electrolytes, and so is dependent on pore fluid presence and nature. Most of earth materials obey the empirical relationship known as Archies law (Eq. 1):
$$ F={\rho}_{\mathrm{w}}/\rho =a{\varphi}^{-m} $$
(1)

ρ w is the water resistivity, ρ is the formation resistivity, a is an empirical constancy (typically 1 for unconsolidated sediments), m is an empirical constant (typically 2 for unconsolidated sediments), φ is the effective porosity, and F is the formation factor related to the volume and tortuosity of the pore space.

2.2 Physical Base

The DCR method is based on the principle that the earth material acts as a resistor in a circuit. After inducing an electrical current into the ground, the ability of that material is measured to resist the current by recording the electrical potential to achieve information on the resistivity structure in the ground. Generally, the current flows in radial form out from the source of current, and the equipotential surfaces forming half spheres run perpendicular to the current flow (Fig. 1).
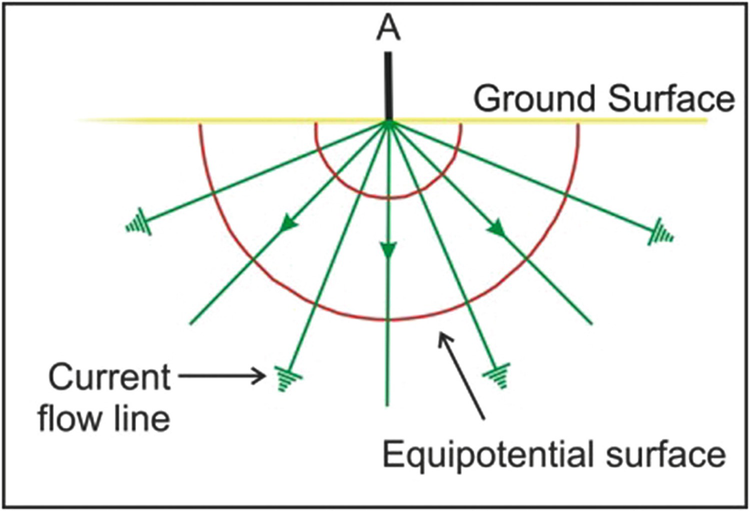
../images/437178_1_En_210_Chapter/437178_1_En_210_Fig1_HTML.png
Fig. 1

Simplified current flow lines and equipotential surfaces arising from a single current source

In the common situation with both a current source and a current sink, the current flow lines and the equipotential surfaces become more complex. Electric field is created in the earth by means of low-frequency AC generators and/or DC batteries. When the electric current is sent by means of two grounded electrode, called current electrodes “A” and “B” placed at two selected points, electrons start to flow through the earth’s subsurface from the negative to the positive terminals of the current source. The potential differences are measured by another two potential electrodes called “M” and “N” (see Fig. 2). If the ground is heterogeneous, the resulting resistivity obtained using Eq. (2) for any of the different types of configurations is called apparent resistivity (ρ a) that constitutes a weighted average of the true resistivity.
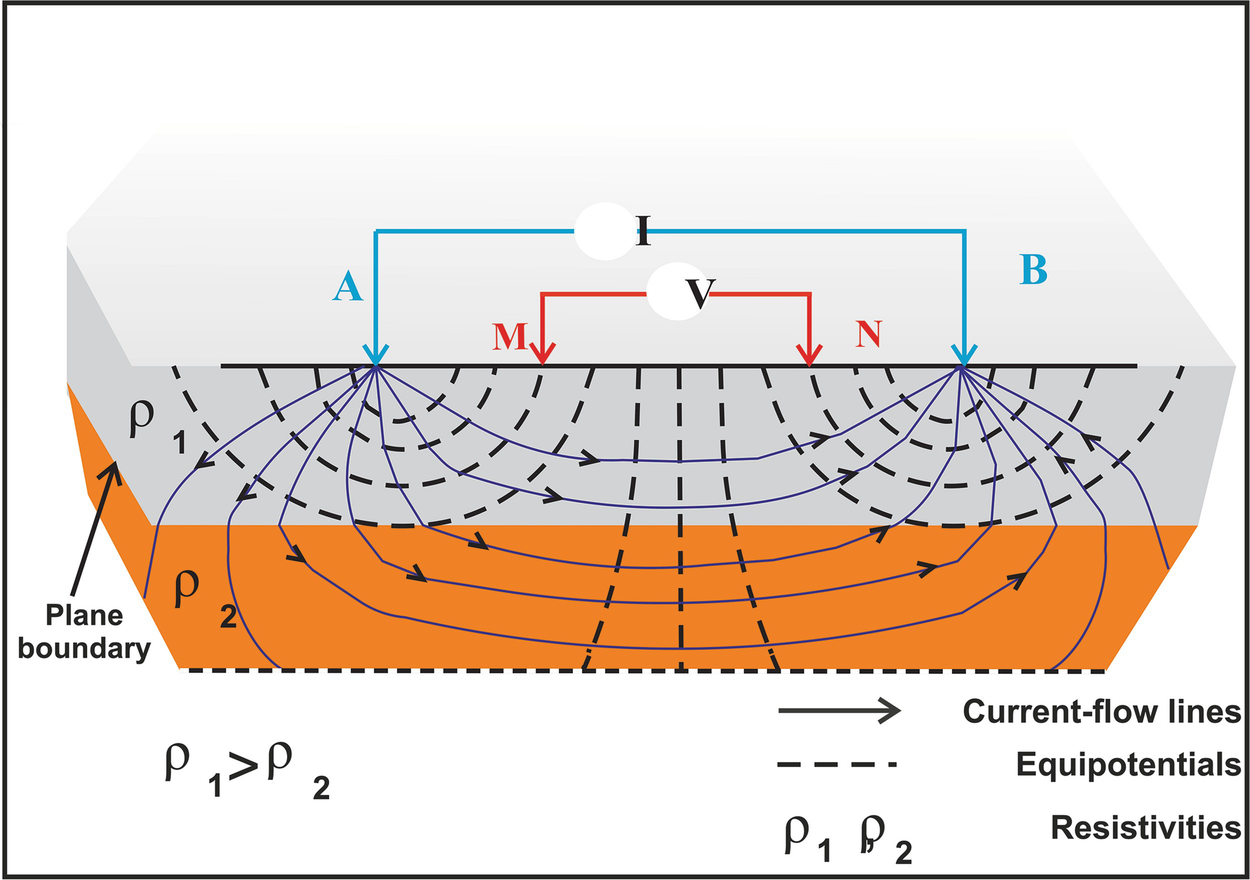
../images/437178_1_En_210_Chapter/437178_1_En_210_Fig2_HTML.png
Fig. 2

Resistivity measurement principles with a four-electrode configuration

Geoelectrical data are commonly expressed as apparent resistivities:
$$ {\rho}_{\mathrm{a}}=K\left(\raisebox{1ex}{$\Delta V$}\!\left/ \!\raisebox{-1ex}{$I$}\right.\right), $$
(2)
where
$$ K=2\pi \left(\frac{1}{r_{\mathrm{AM}}}-\frac{1}{r_{\mathrm{AN}}}-\frac{1}{r_{\mathrm{BM}}}+\frac{1}{r_{\mathrm{BN}}}\right) $$

where K is the geometrical factor having the dimension of length (m), which depends on the arrangement of the four electrodes.

The IP method is considered as an extension to the well-known geoelectric technique. It is usually assumed that IP and DCR measurements have been measured simultaneously. The IP method depends mainly on a small amount of electric charge storage when a current is passed through the rock, to be released and measured when the current is switched off. Generally speaking, the IP measurements became more established in the last 20 years.

In time domain IP, the ratio of overvoltage (V p) to observed voltage (V 0) is measured, and this ratio is known as chargeability (M), which is expressed in millivolts per volt or percent:
$$ M=\frac{V_p}{V_0}\kern0.5em \mathrm{and}\kern0.5em M=\frac{1}{V_0}\underset{t1}{\overset{t2}{\int }}{V}_{p(t)} dt=\frac{A}{V_0} $$
(3)
In frequency-domain IP, apparent resistivity at two or more AC frequencies is measured. Accordingly, the IP effect is well described by the so-called frequency effect FE (unitless):
$$ \mathrm{FE}=\frac{\rho_0-{\rho}_{\infty }}{\kern0.5em {\rho}_{\infty }}, $$
(4)
where ρ 0 is the apparent resistivity at low frequency and ρ ∞ is the apparent resistivity at a higher frequency. Both M and FE are easily interrelated and they can be expressed as
$$ M=\frac{\mathrm{FE}}{1+\mathrm{FE}}=\frac{\rho_0-{\rho}_{\infty }}{\kern0.5em {\rho}_0} $$
(5)

In the spectral induced polarization (SIP) method, the resistivity/conductivity magnitude and phase shift are measured over a wide range of frequencies (0.625 Hz to 10 kHz).

In the SIP method, the fundamental quantities of interest are the electrical conductivity magnitude |σ(ω)| and phase φ(ω) (or the equivalent real and imaginary parts of conductivity) of complex conductivity as a function of frequency as
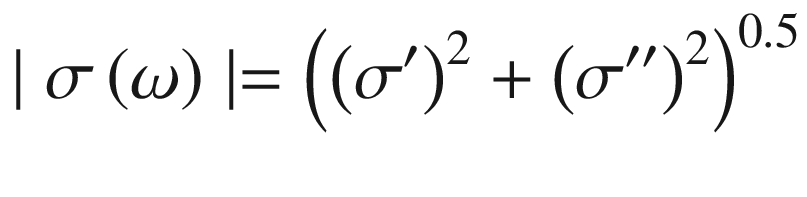
$$ \mid \sigma \left(\omega \right)\mid ={\left({\left({\sigma}^{\prime}\right)}^2+{\left({\sigma}^{{\prime\prime}}\right)}^2\right)}^{0.5} $$
(6)
$$ {\sigma}^{\prime }=\left|\sigma \left(\omega \right)\right|\cos \varphi \kern0.5em \mathrm{and}\kern0.5em {\sigma}^{{\prime\prime} }=\left|\sigma \left(\omega \right)\right|\sin \varphi, $$
(7)

where ω is the angular frequency and σ′ and σ″ are the real and imaginary parts of the electrical conductivity, respectively.

SIP method is based on the change of electrochemical and electronic conductivity in the pore spaces of the rocks and soil [17]. Recent reviews of the method, including a discussion of the underlying mechanisms, are given by [18, 19]. Figure 3 shows three polarization mechanisms associated with the mineral grain polarization coated by an electrical double layer (EDL) coating grain surface [21]. They include (1) the diffuse layer deformation at a very high frequency >10 kHz see the so-called Debye–Falkenhagen effect; Falkenhagen [22]), (2) the Stern layer polarization [23, 24], and (3) the diffusion or membrane polarization, which is related to the difference in the transference number for the cations and anions during their migration in the porous material [25, 26].
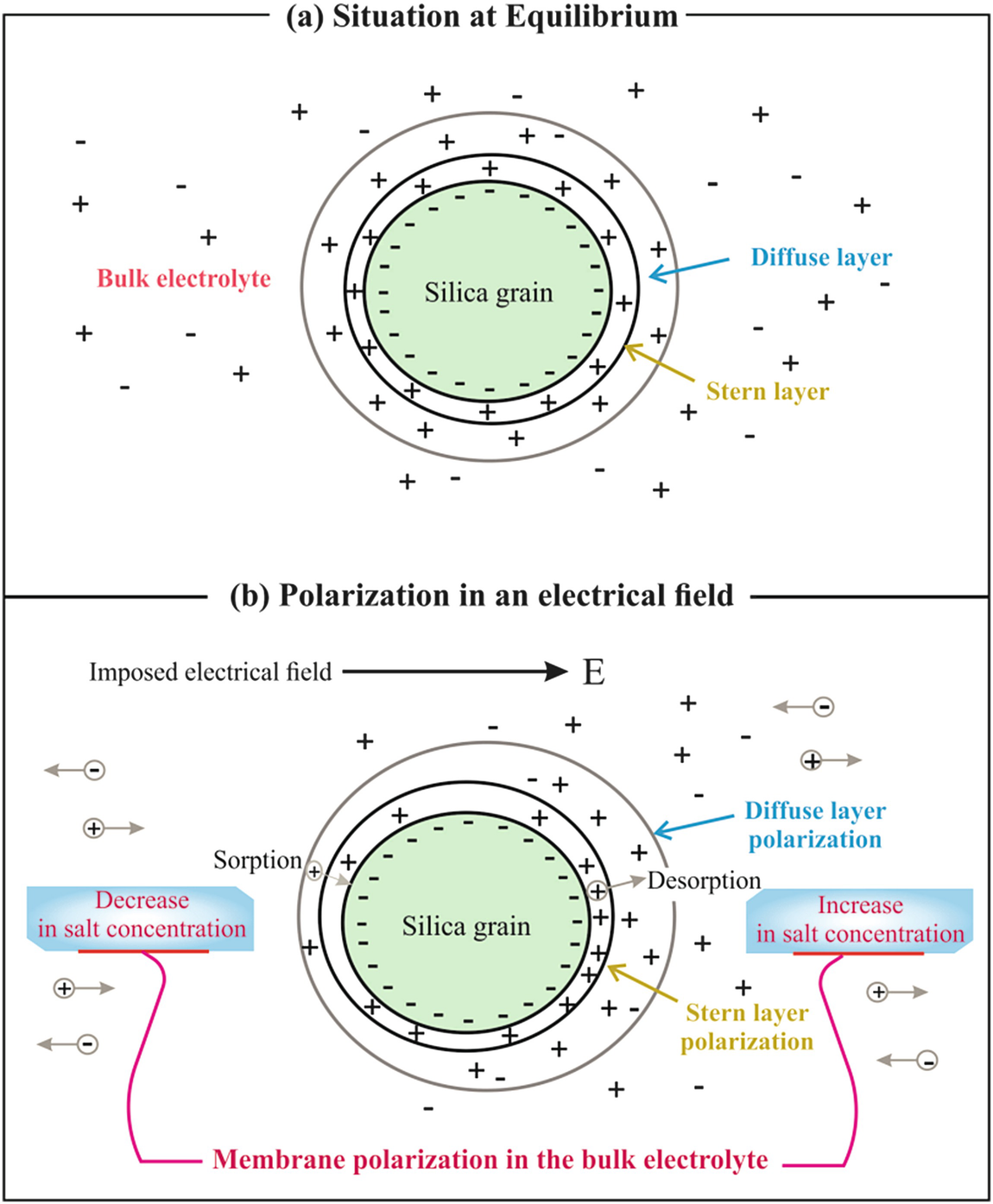
../images/437178_1_En_210_Chapter/437178_1_En_210_Fig3_HTML.png
Fig. 3

A single grain polarization. (a) Electrical double layer (Stern plus diffuse layers) at equilibrium. (b) Polarization mechanisms of the grain under an electrical field E (modified after [20]).

2.3 Electrode Arrays and Field Techniques

There are common electrode configurations (i.e., arrangements) for placing the potentials and current electrodes for field surveying. These electrode arrays for geologic investigation are Schlumberger (SC), Wenner (MN), and dipole-dipole (DD) and pole-dipole (PD) array (Fig. 4). The choice of such arrays for a field survey depends on:
  1. 1.

    The structure types to be mapped, the resistivity instrument sensitivity, the noise level, the signal strength, and the data coverage

     
  2. 2.

    The array sensitivity to vertical and horizontal changes in the subsurface resistivity (e.g., [27])

     
  3. 3.

    The depth of investigation (DOI) [28]

     
  4. 4.

    The array resolution for horizontal and dipping layers and sensitivity to surface heterogeneous [29]

     
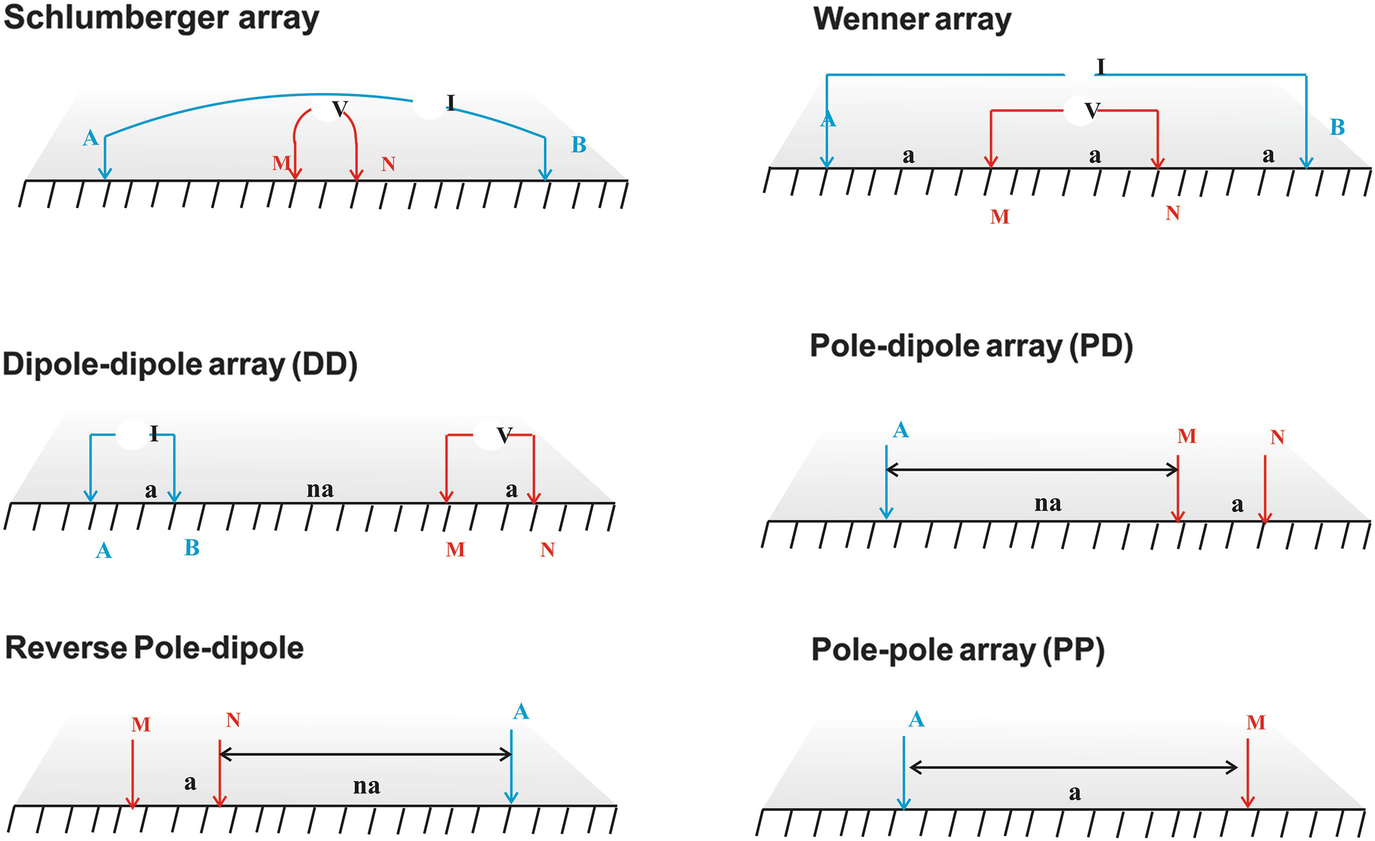
../images/437178_1_En_210_Chapter/437178_1_En_210_Fig4_HTML.png
Fig. 4

Some of the most commonly used electrode arrays. The letters A and B designate the current electrodes, and the letters M and N denote the potential electrodes

The geoelectrical data acquisition can be carried out using three field techniques: (1) single electrical sounding (SES), (2) continuous electrical sounding (CES), and (3) pulled array continuous electrical sounding (PACES). The SES is applied to determine the resistivity variation with depth. SES is typically carried out using Schlumberger array (Fig. 4), since the ES curve can be interpreted using a 1D horizontally layered earth model. In the CES, electrical resistivity data along a profile is obtained (Fig. 5). The CES measurement’s advantage is their high lateral and vertical resolution along the profile. Accordingly, CES combines the profiling and sounding surveys. On the contrary to SES, a large number of electrode arrays can be used along with a straight line. The CES data are then used for the forward and inverse modeling programs that produce the resistivity depth sections (i.e., 2D section). In the PACES, a small caterpillar drags a set (i.e., tail) of electrodes along with the processing electronics. Eight electrode arrays can be acquired simultaneously permitting for electrical sounding data to be measured continuously along the profile (Fig. 6). Further, digital data measurements can be carried out online by equipment on the caterpillar. The system in PACES has the ability to determine the inadequate galvanic contact at the potential current electrodes.
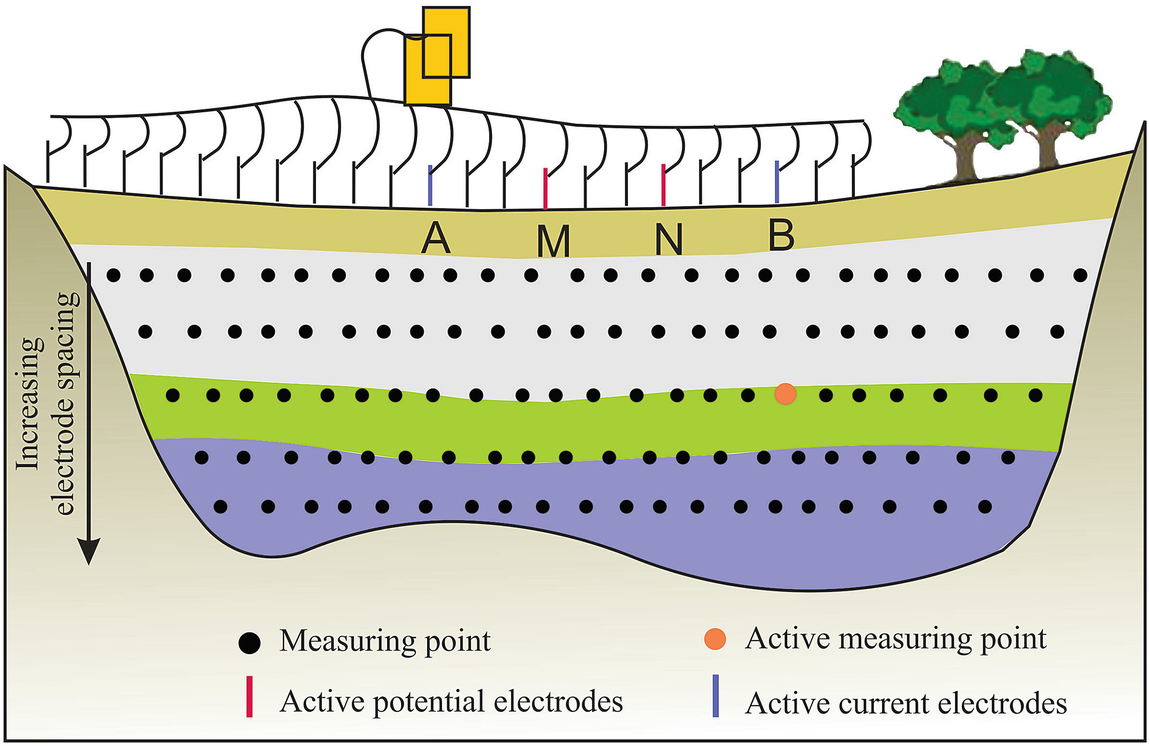
../images/437178_1_En_210_Chapter/437178_1_En_210_Fig5_HTML.png
Fig. 5

A schematic model of the CES technique and data density using Wenner array

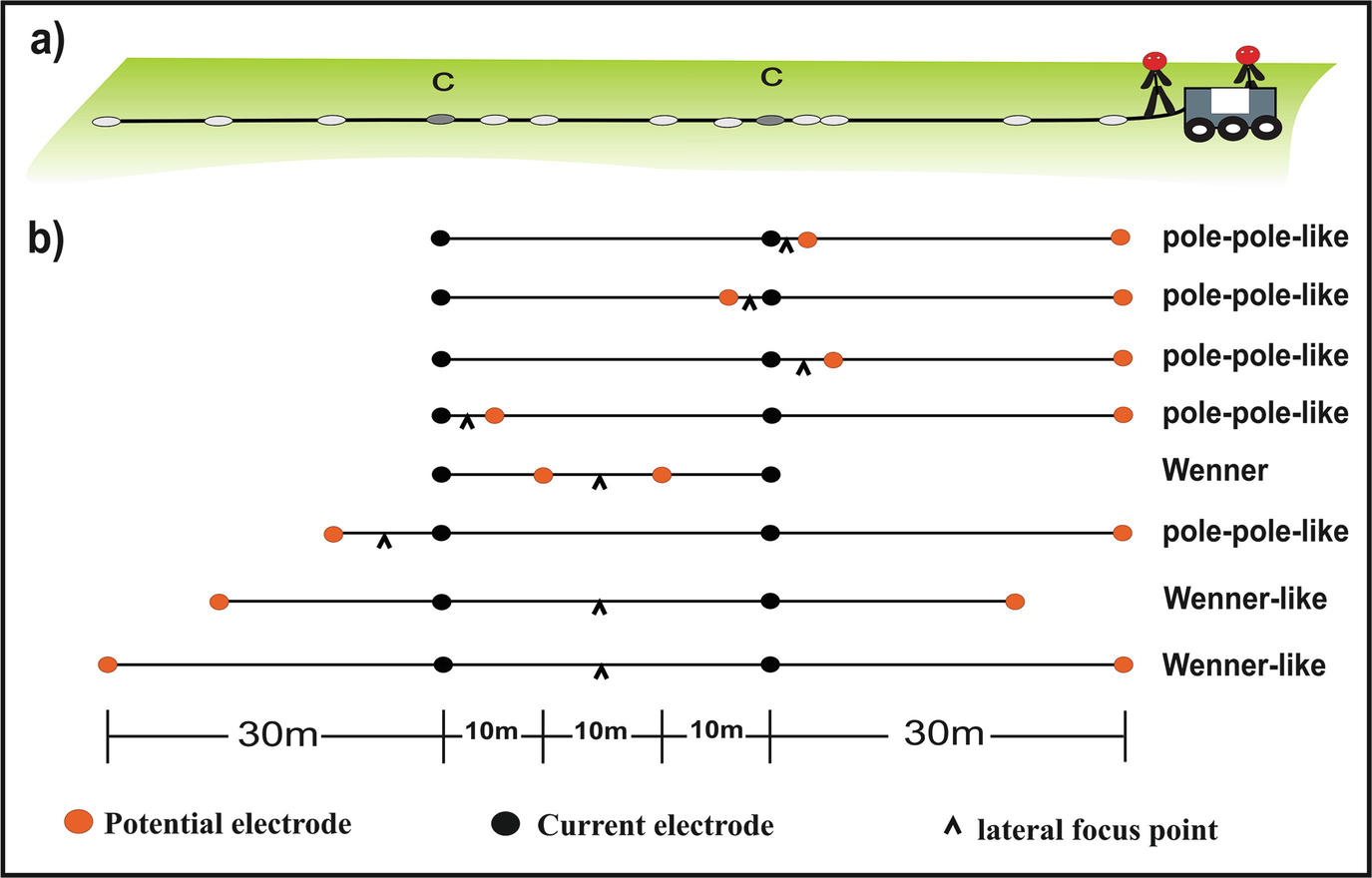
../images/437178_1_En_210_Chapter/437178_1_En_210_Fig6_HTML.png
Fig. 6

A schematic model of the PACES system (a) showing the pulled electrodes by a small caterpillar using eight-electrode configurations (b)

2.4 Hydraulic Conductivity Prediction

For clay-free porous media, i.e., uniformly sized particles, the relaxation time constant, τ, of IP decay curve can be given by [30, 31]
$$ \tau =\frac{L^2}{D}, $$
(8)
where L is the relaxation distance along the applied electric field and D is the coefficient of diffusion. Accordingly, the pore radius, R, can be calculated by
$$ R={\left( D\tau \right)}^{0.5}, $$
(9)
The earth material’s geoelectrical properties may be represented by complex resistivity (ρ *):
$$ {\rho}^{\ast }={\rho}^{\prime }+i{\rho}^{{\prime\prime} }, $$
(10)
where ρ′ and ρ″ are the real and the imaginary resistivity parts, respectively, of ρ * and φ is the phase shift of ρ * that can be also given as follows:
$$ \varphi =\arctan \left({\rho}^{{\prime\prime} }/{\rho}^{\prime}\right) $$
(11)
Generally speaking, the ρ′ (i.e., DC resistivity) has been commonly used to estimate hydraulic conductivity (K) value for unconsolidated aquifers. Positive or negative linear log-log relationships between ρ′ and K were explained by [27]
$$ K=a{\left({\rho}^{\prime}\right)}^b $$
(12)

The correlation of K with ρ′ is directly proportional on a large scale for sandy-clayey aquifer [11]. On a local scale, sometimes, such correlation is inversely proportional [32].

Many literatures [11, 33] demonstrating a power law dependence of ρ′ on specific surface area (S por) [34] indicated that the φ was particularly constant over a wide range of frequency and presented an empirical relationship to estimate K for a single frequency value, around 1 Hz. The proposed model, “Börner model,” to calculate K (m/s) for a constant phase angle (CPA) is
$$ K=\frac{a}{F{\left({S}_{\mathrm{por}}\right)}^c}, $$
(13)
where exponents a and c are adjustable parameters and F is the formation factor.
The exponent “a” is equal to 0.00475 [35] and 1 [34] for consolidated and unconsolidated sediments, respectively. The exponent a = 0.00475 was recommended by [36] for unconsolidated sediments. Further, the exponent “c” was formulated in the range of 2.8 < c < 4.6 by [34] regarding the method of K measurements. The F can be calculated using [34]
$$ F=\frac{\sigma_{\mathrm{w}}}{\sigma^{\prime }-{\sigma}^{{\prime\prime} }/\mathrm{l}} $$
(14)
where σ w is the conductivity of pore fluid. For unconsolidated sandy aquifer, S por can be calculated [18] as
$$ {S}_{\mathrm{por}}={\left(\frac{\sigma^{{\prime\prime} }}{0.0101}\right)}^{1/0.916}, $$
(15)

where σ″ in mS/m and Spor is in μm−1.

Slater and Lesmes [37] suggested another approach to calculate K by using the CPA model. The suggested model is based on a relation between the ρ″ with the grain diameter regarding the smallest 10% portion (i.e., d10) of the soil sample. Additionally, this method shows an inverse linear relation between σ″ and K around 1 Hz (Slater model):
$$ K=\frac{m}{{\left({\sigma}^{{\prime\prime}}\right)}^n} $$
(16)

where σ″ is given in μS/m. m and n are adjustable parameters with m = (2.0 ± 0.3) 10–4; n = 1.1 ± 0.2, and K is in m/s.

It is generally accepted that τ(tau) is controlled by the diffusion process [20] in the electrochemical double layer (EDL). A power law relationship between some relaxation time constants and permeability (k) has been reported in published data sets:
$$ k=a{\tau}^b, $$
(17)

where a and b are formation-specific parameters.

A power law relationship between the mean relaxation time (τm) and S por was established by [38]. In case of a weak relation between τ and permeability (k) and/or K, this relation cannot be applied. Furthermore, [18] derived an empirical power law relationship to predict k as a function of conductivity σ″, chargeability M and τm, which are derived from DD:
$$ k=a\cdot {\left({\rho}^{\prime}\right)}^b\cdot {M}^c\cdot {\left({\tau}_m\right)}^d. $$
(18)

The four empirical parameters a, b, c, and d are determined by a multivariate regression analysis.

Based on the Debye decomposition (DD) of IP spectra, [11] proposed a power law relationship in the form of
$$ K=A\left({\rho}^{\prime}\right)B(t)C, $$
(19)
where the A coefficient and the B and C exponents are determined by a regression analysis of the logarithmic quantities τ and K. This methodology was adopted for the estimation of the K when there is a general trend of increasing or decreasing both individual ρ′ and τ with K.

2.5 Geoelectrical Data Inversion

Many researchers discussed the geoelectrical data interpretation techniques in order to solve a wide range of complex inverse problems (e.g., [29]). The main goal of geoelectrical interpretation is to define the electrical property distributions inside the earth from a set of measurements, which can be mathematically modeled from physical laws, e.g., Poisson and Laplace’s equations. Figure 7 illustrates the interpretation process of geoelectrical data, which depends mainly on solving the forward and inverse problems. In the forward problem, the link between the model parameters and the model response (2D and 3D resistivity models) are solved by applying finite-difference or finite-element techniques (e.g., [39]). In both techniques, the resistivity distribution is approximated using a mesh of cells or individual elements with constant resistivity value.
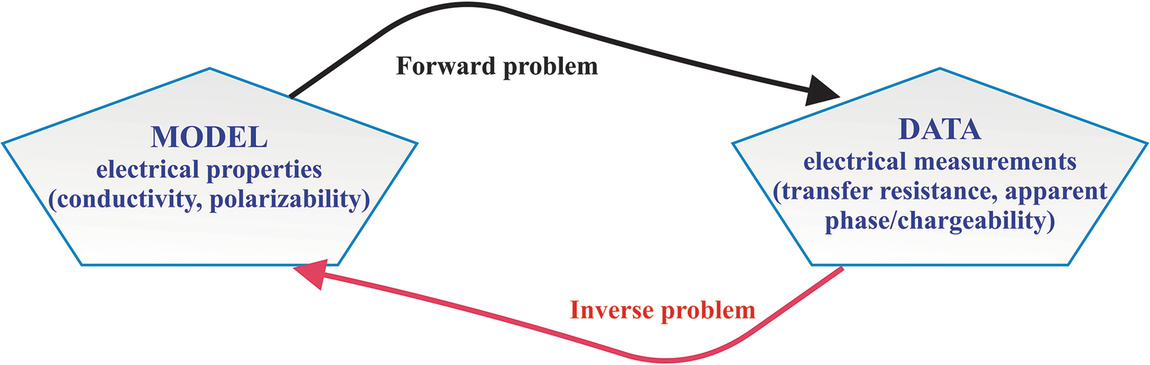
../images/437178_1_En_210_Chapter/437178_1_En_210_Fig7_HTML.png
Fig. 7

DCR interpretation process in the form of forward and inverse problems

The current commonly inversion approaches depend on mainly derivative-based inversion (DBI) methods [40]. In such conventional inversion schemes, the 2D forward calculations are constructed of small cells to construct 2D model. In general, the parameterization jointly with a 2D regularization usually represents a smooth and/or blurred image of the measured subsurface structures, which is known as the smearing [41]. Consequently, new parameterizations were developed for subsurface layers extraction with sharp boundaries [42]. Recently, model in the form of some interfaces can be used to represent the subsurface layers more consistent with the actual geological condition named as “structure-based (SB) model” [43]. For example, Fig. 8 shows the inverted ERTs using DBI and nonconventional with SB model approaches compared with the drilled borehole data at a new development area (Tenth of Ramadan City), Egypt, to image near-surface lateral heterogeneity. It is clear that the control point number (i.e., turquoise color lines) and the node point number (pink dots over white circles) representing the subsurface layers were suggested by the borehole data and the visual inspection of the 2D-ERT using DBI method.
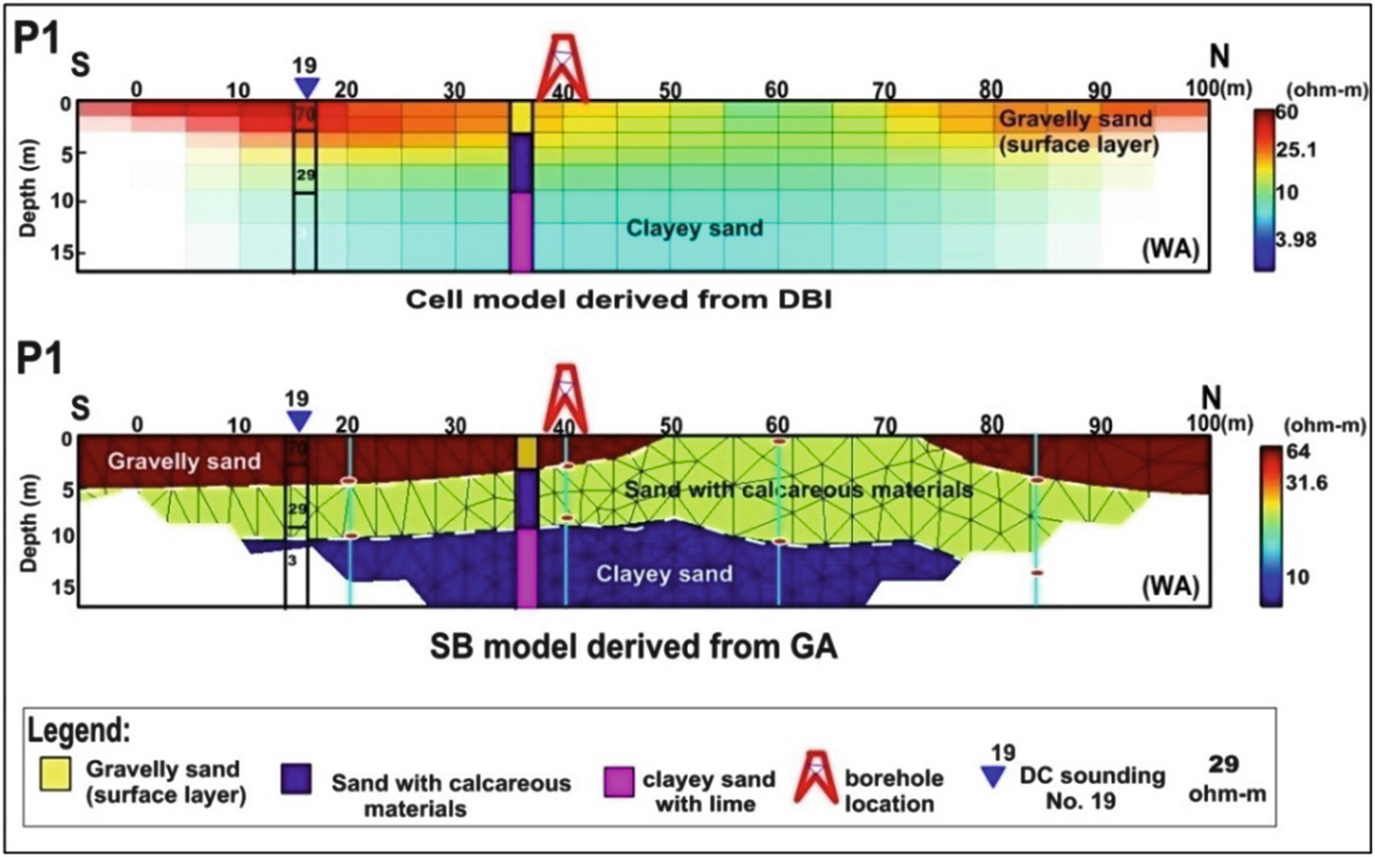
../images/437178_1_En_210_Chapter/437178_1_En_210_Fig8_HTML.png
Fig. 8

2D ERTs obtained from Wenner alpha (WA) data using (top) DBI method and (bottom) nonconventional inversion method produced by GA and structure-based (SB) model. Note that (bottom) all model nodes (pink dots over white circle) along the control points (turquoise color) defining the layer interfaces were derived from the borehole information and the preliminary DBI results

The genetic algorithim (GA) and stochastic techniques belong to the same family of global optimization (GO) algorithms. The main difference between GO and the conventional DBI is the way of data use. In the DBI methods, the differences between observed and calculated data are converted to the parameter discrepancies applying an operator called generalized inverse at each iteration step. In the GO methods, the data are not used in model update and creation. The parameter update way depends on the global minimization type. Generally speaking, the GA generates model updates by the biological process simulation and can verify a huge distinct and complicated model number. Figure 9 shows an example of DCR sounding inversion using GA, and the inversion results were calibrated with the borehole data in Atfih area, Eastern Desert (ED), Egypt.
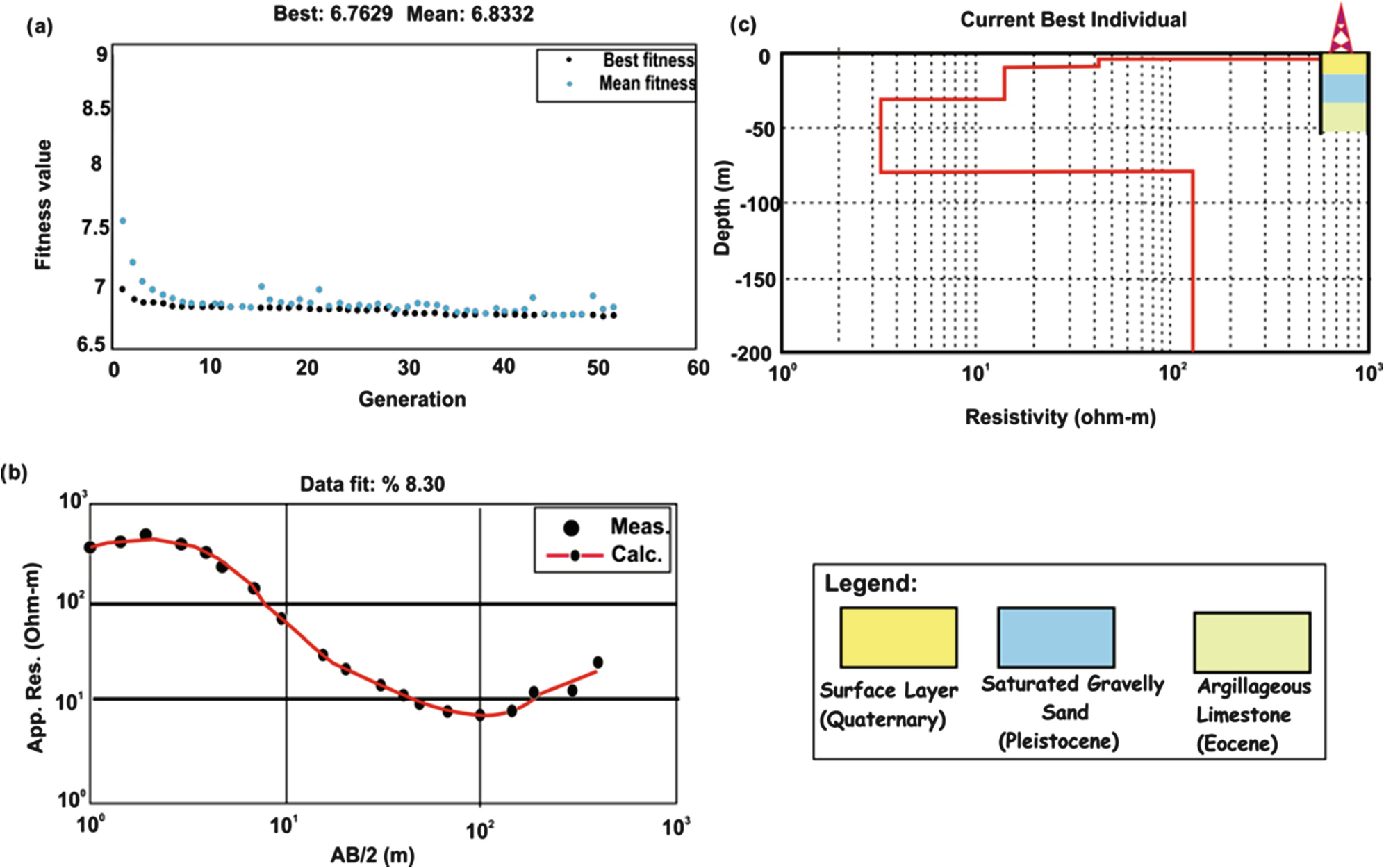
../images/437178_1_En_210_Chapter/437178_1_En_210_Fig9_HTML.png
Fig. 9

The interpreted resistivity layers constrained with the geological data using a genetic algorithm (GA); (a) variations of mean and best misfit versus generation; (b) a comparison between the measured and calculated data at the best misfit value; (c) a comparison between the model response and borehole information

3 Applications to the Nile Delta

In the northern part of East Nile Delta (coastal area), Egypt, fresh groundwater salinization is a noticeable aspect of in groundwater quality salinization. Notably, saltwater intrusion has affected irrigation and domestic wells. Furthermore, human activity affects the salt transport. Accordingly, the main goal of the study was to delineate the saltwater intrusion due to the intensive pumping in the transition zone of eastern Nile Delta aquifer. In the course of this study, the 1D model generation using a hybrid genetic algorithm (GA) is applied and tested using borehole information. The constructed geoelectrical cross sections emphasize and delineate the extension of saltwater intrusion (Figs. 10 and 11). Cleary, it is found that due to excessive pumping from shallow wells over the last decades, the subsurface resistivity and TDS distributions can change rapidly within a short distance. Additionally, the results show that despite the dominance of brackish and saltwater at the northern part of the area, perched low conductive lenses are observed reflecting a low level of groundwater salinization. To obtain a link between water salinity and aquifer resistivity, an empirical relationship is derived to predicate the salinity variations at different depths [4]. In comparison with the measured TDS, the predicted salinity map appears realistic. These results demonstrate the important role of the integration between resistivity and salinity measurements for mapping the groundwater salinization with depth and call a further research to plan and manage the area’s water resources.
../images/437178_1_En_210_Chapter/437178_1_En_210_Fig10_HTML.png
Fig. 10

3D visualization resistivity model represents the resistivity distributions at the northern part of the East Nile Delta, Egypt [4]

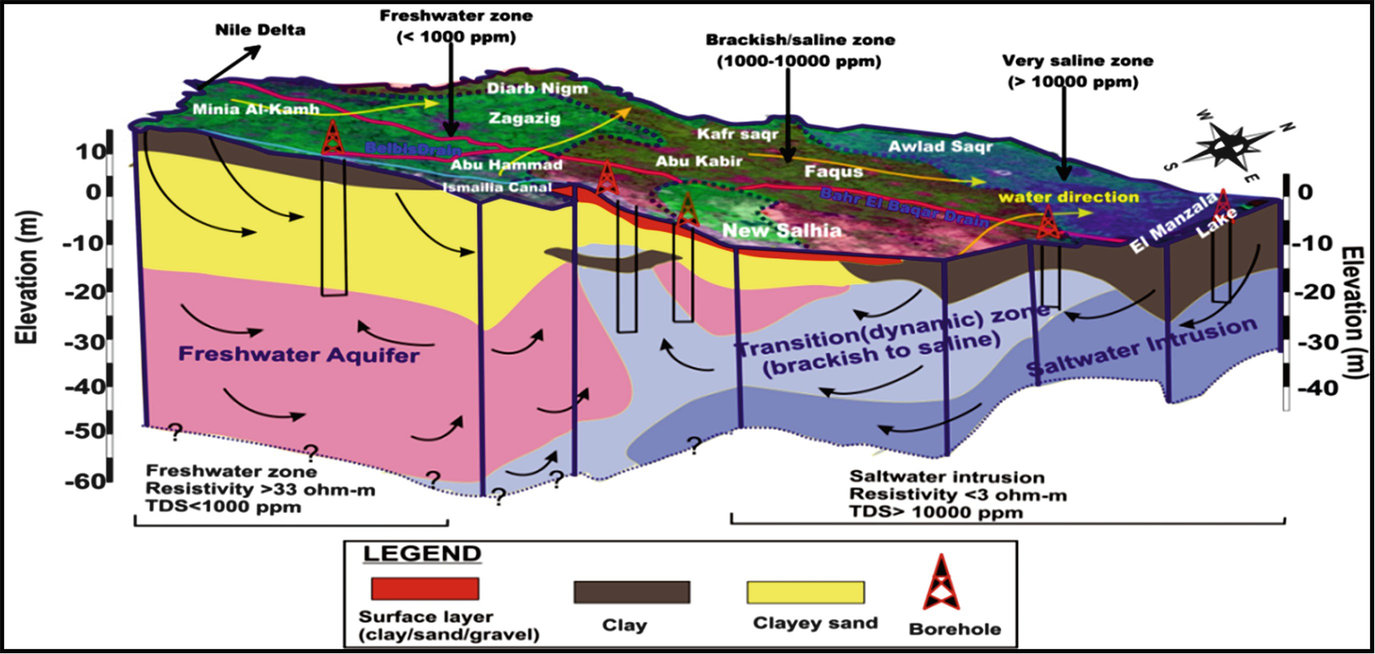
../images/437178_1_En_210_Chapter/437178_1_En_210_Fig11_HTML.png
Fig. 11

3D schematic model shows the freshwater/saltwater conditions at a coastal area, East Nile Delta, Egypt [4]

Furthermore, the aquifer salinity can be predicted using the aquifer resistivity values applying a polynomial relationship, inverse first order, of both true aquifer resistivities and the measured TDS values [4]. Figure 12 shows the polynomial relationship to predict the TDS values at the northern part of East Nile Delta using 12 data points of DCR soundings and TDS values close to the observed boreholes. Notably, the TDS prediction proves the reliability of the inverted DCR data uses to predict TDS clues with various depth using the polynomial equation over the northern coastal area of East Nile Delta.
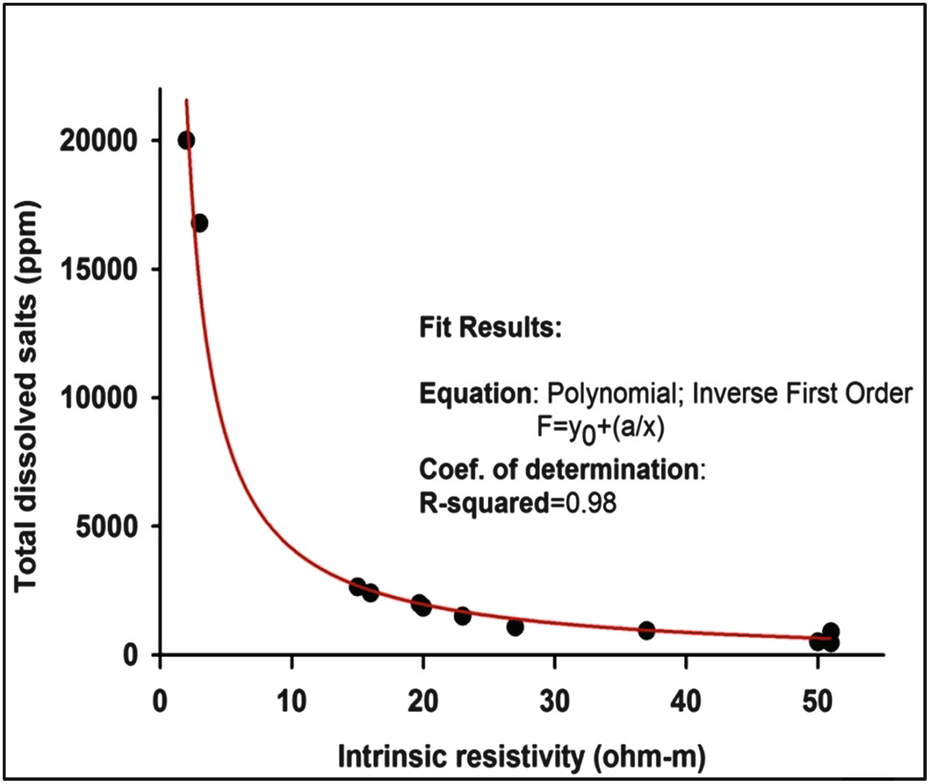
../images/437178_1_En_210_Chapter/437178_1_En_210_Fig12_HTML.png
Fig. 12

Correlation between true resistivity derived from DCR sounding inversion and TDS of some collected water samples at the northern coastal part of East Nile Delta [4]

The East Nile Delta, Egypt (Fig. 13), is characterized by different geological and hydrogeological complexity conditions. Geomorphologically, the East Nile Delta decreases in elevation northward, i.e., relatively low topography (~4 m). On the other hand, the southern parts have high features with steeper slopes. Attwa et al. [2] show the efficiency of DCR soundings to identify the geometry and nature of aquifers (Fig. 14). Regionally, the inversion results of DCR soundings represent the water-bearing formations and the main structures in the form of folds and faults. Figure 14 indicates two aquifers; main Quaternary aquifer overlies the deep saline Tertiary. Further, the Quaternary groundwater-bearing formations become the main aquifer in the central part of East Nile Delta. On the other hand, Miocene aquifer represents the main aquifer in the southern portion.
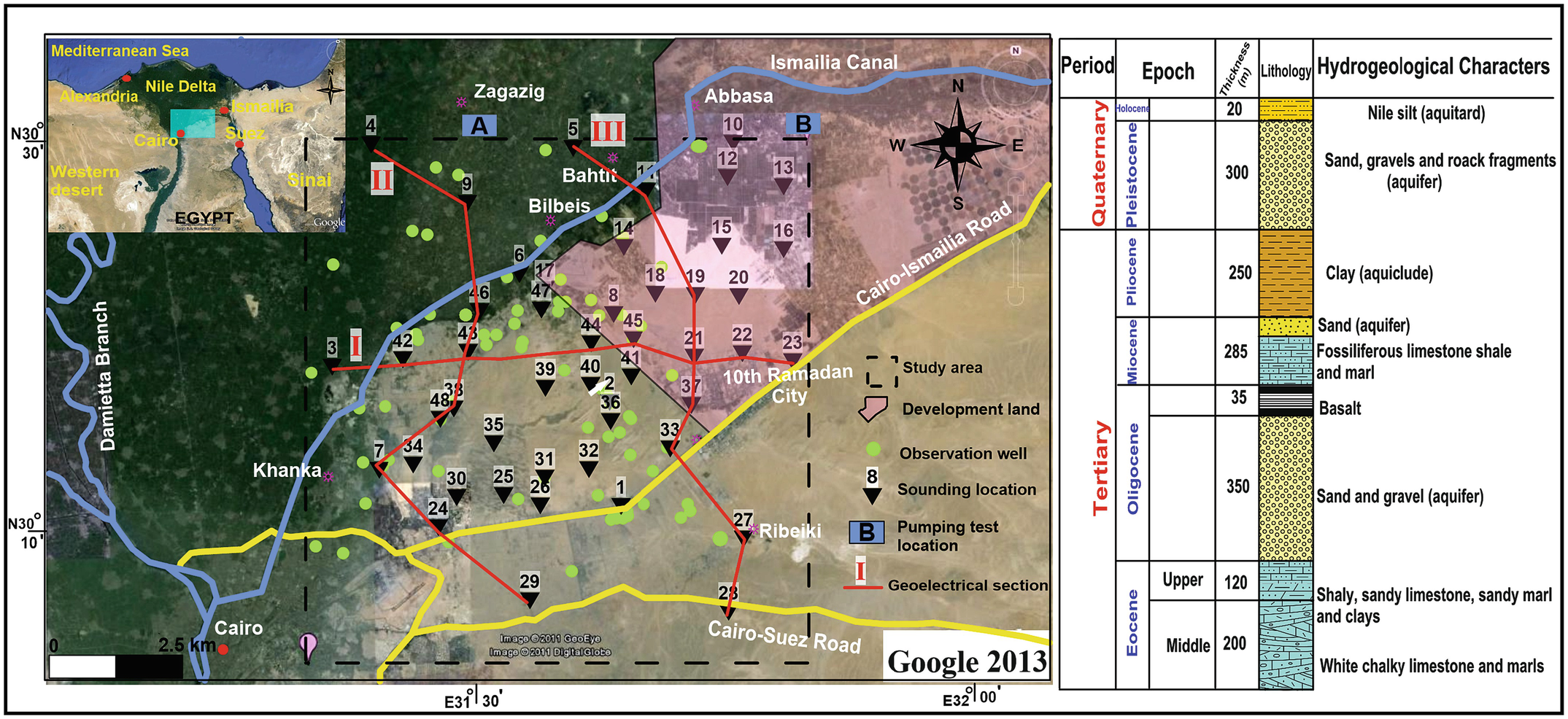
../images/437178_1_En_210_Chapter/437178_1_En_210_Fig13_HTML.png
Fig. 13

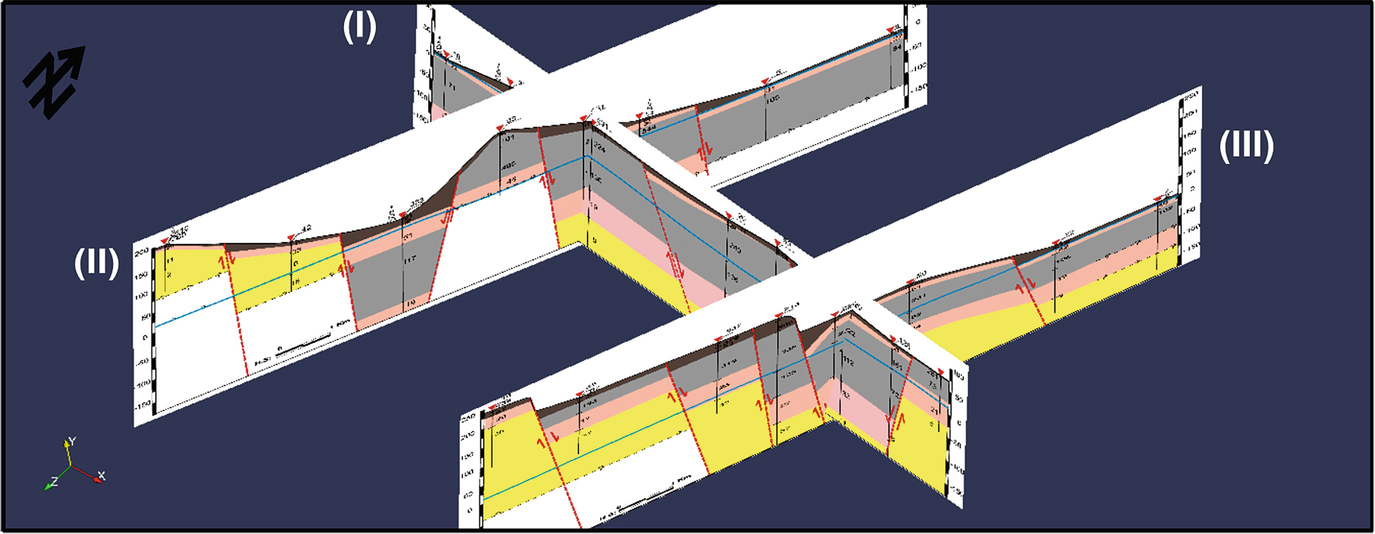
Location map of the East Nile Delta showing the DCR soundings, geoelectrical cross section, and observed boreholes (left panel). Compiles stratigraphic section (right panel) of the East Nile Delta

../images/437178_1_En_210_Chapter/437178_1_En_210_Fig14_HTML.png
Fig. 14

Geoelectrical cross sections in the form of 3D fence diagram at East Nile Delta (for location, see Fig. 11, left) [2]

Hydrogeologically, the aquifer hydraulic conductivity (K) can be predicted using the power law relation between hydraulic conductivity and aquifer resistivity (Eq. 12). Figure 15 shows log-log plot of aquifer resistivity of Quaternary and Miocene aquifers versus the observed K. It is clear that there is a general trend of increasing aquifer resistivity with increasing K. Accordingly, the K estimation from individual aquifer resistivity appears to be applicable.
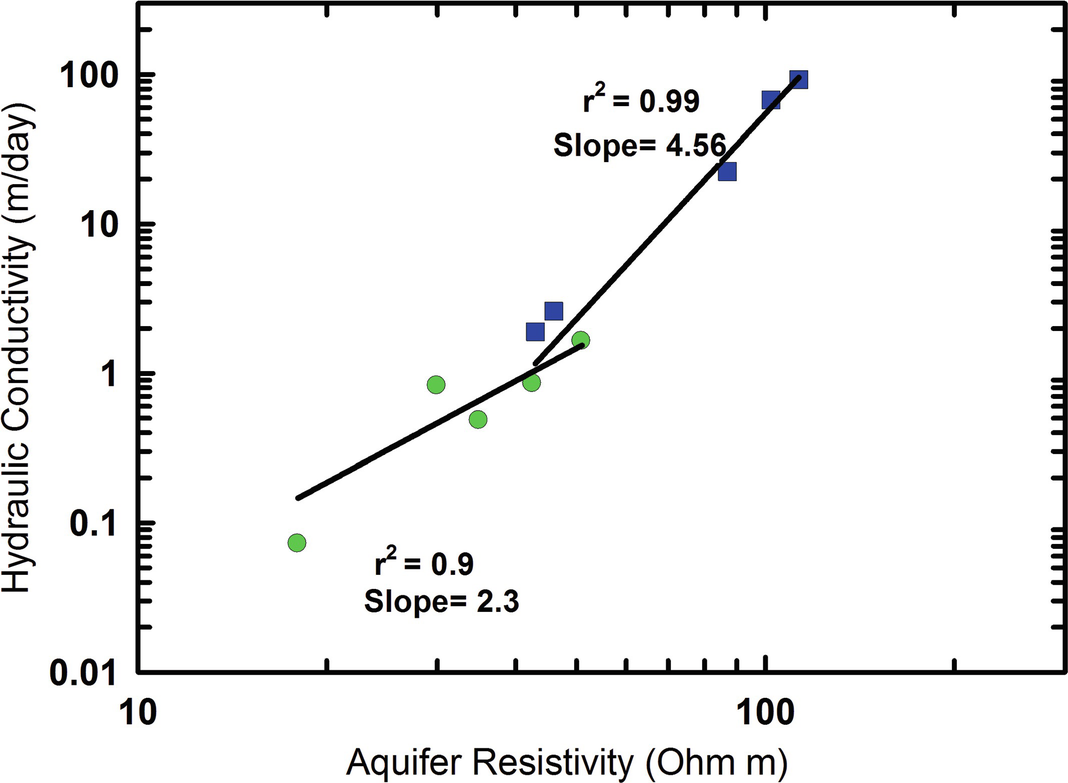
../images/437178_1_En_210_Chapter/437178_1_En_210_Fig15_HTML.png
Fig. 15

The aquifer resistivity vs. the hydraulic conductivity (K) of ten DCR soundings and observed boreholes. Blue solid squares indicate Quaternary aquifer, while the Tertiary aquifer is represented by green solid circles [2]

4 Conclusions and Recommendations

The chapter shows that the application of DCR method with available boreholes, an integrative approach, is valuable in hydrogeological conditions assessment in East Nile Delta, Egypt. Based on the present studies from East Nile Delta, the results proved (1) the efficiency of the DCR method for hydrogeological evaluation in costal semiarid areas and (2) the validity of the DCR method to predict the TDS and K using the empirical relationships for this area. Furthermore, the joint use of the conventional and nonconventional inversion techniques is recommended for hydrogeological evaluation in East Nile Delta. In the ongoing research, the computational speed of GA requires to be improved applying parallel computation. Further research including pumping tests is required to verify the prediction of hydraulic conductivity using the geoelectrical empirical relationships in East Nile Delta. Additionally the derived salinity equation modification is desirable considering the clay content ratio and grain size analysis. Therefore, it is worthwhile to mention that the DCR method has a great importance for hydrogeological assessment to the decision-makers.