The Shapes of Space
Stand up and look around. Walk in a circle. Jump in the air. Wave your arms. You are a collection of particles moving about within a small region of a 3-manifold—a three-dimensional space—that extends in all directions for many billions of light-years.
Manifolds are mathematical constructs. The triumph of physics since the time of Galileo and Kepler has been the successful description of reality by mathematics of one flavor or another, such as the mathematics of manifolds. According to physics, everything that happens takes place against the backdrop of three-dimensional space (leaving aside the speculations of string theorists that there are tiny dimensions in addition to the three that are manifest). Three dimensions means that three numbers are needed to specify the location of a particle. Near Earth, for instance, the three numbers could be latitude, longitude and altitude.
According to Newtonian physics and traditional quantum physics, the three-dimensional space where everything happens is fixed and immutable. Einstein’s theory of general relativity, in contrast, makes space an active player: the distance from one point to another is influenced by how much matter and energy are nearby and by any gravitational waves that may be passing by. But whether we are dealing with Newtonian or Einsteinian physics and whether space is infinite or finite, space is represented by a 3-manifold. Understanding the properties of 3-manifolds is therefore essential for fully comprehending the foundations on which almost all of physics—and all other sciences—are built. (The 4-manifolds are also important: space and time together form a 4-manifold.)
Mathematicians know a lot about 3-manifolds, yet some of the most basic questions have proved to be the hardest. The branch of mathematics that studies manifolds is topology. Among the fundamental questions topologists can ask about 3-manifolds are: What is the simplest type of 3-manifold, the one with the least complicated structure? Does it have many cousins that are equally simple, or is it unique? What kinds of 3-manifolds are there?
The answer to the first of those questions has long been known: a space called the 3-sphere is the simplest compact 3-manifold. (Noncompact manifolds can be thought of as being infinite or having an edge. Hereafter I consider only compact manifolds.) The other two questions have been up for grabs for a century but may have been answered in 2002 by Grigori (“Grisha”) Perelman, a Russian mathematician who has most probably proved a theorem known as the Poincaré conjecture.
First postulated by French mathematician Henri Poincaré exactly 100 years ago, the conjecture holds that the 3-sphere is unique among 3-manifolds; no other 3-manifold shares the properties that make it so simple. The 3-manifolds that are more complicated than the 3- sphere have boundaries that you can run up against like a brick wall, or multiple connections from one region to another, like a path through the woods that splits and later rejoins. The Poincaré conjecture states that the 3-sphere is the only compact 3-manifold that lacks all those complications. Any three-dimensional object that shares those properties with the sphere can therefore be morphed into the same shape as a 3-sphere; so far as topologists are concerned, the object is just another copy of the 3-sphere. Perelman’s proof also answers the third of our questions: it completes work that classifies all the types of 3-manifolds that exist.
It takes some mental gymnastics to imagine what a 3-sphere is like—it is not simply a sphere in the everyday sense of the word. But it has many properties in common with the 2-sphere, which we are all familiar with: If you take a spherical balloon, the rubber of the balloon forms a 2-sphere. The 2-sphere is two-dimensional because only two coordinates—latitude and longitude—are needed to specify a point on it. Also, if you take a very small disk of the balloon and examine it with a magnifying glass, the disk looks a lot like one cut from a flat two-dimensional plane of rubber. It just has a slight curvature. To a tiny insect crawling on the balloon, it would seem like a flat plane. Yet if the insect traveled far enough in what would seem to it to be a straight line, eventually it would arrive back at its starting point.
Similarly, a gnat in a 3-sphere—or a person in one as big as our universe!—perceives itself to be in “ordinary” three-dimensional space. But if it flies far enough in a straight line in any direction, eventually it will circumnavigate the 3-sphere and find itself back where it started, just like the insect on the balloon or someone taking a trip around the world.
Spheres exist for dimensions other than three as well. The 1-sphere is also familiar to you: it is just a circle (the rim of a disk, not the disk itself). The n-dimensional sphere is called an n-sphere.
Multidimensional Music of Spheres
The 3-sphere at the heart of Poincaré’s conjecture takes a bit of effort to visualize. Mathematicians who prove theorems about higher-dimensional spaces do not have to visualize them. They make do with abstract properties, guided by intuitive notions based on analogies to lower dimensions (but being careful not to take the analogies literally). Others, too, can form an idea of what higher-dimensional objects are like by working up from familiar lower-dimensional examples. The 3-sphere is a case in point.


Proving Conjectures
After Poincaré proposed his conjecture about the 3-sphere, half a century went by before any real progress was made in proving it. In the 1960s mathematicians proved analogues of the conjecture for spheres of five dimensions or more. In each case, the n-sphere is the unique, simplest manifold of that dimensionality. Paradoxically, this result was easier to prove for higher-dimensional spheres than for those of four or three dimensions. The proof for the particularly difficult case of four dimensions came in 1982. Only the original three-dimensional case involving Poincaré’s 3-sphere remained open.
A major step in closing the three-dimensional problem came in November 2002, when Perelman, a mathematician at the Steklov Institute of Mathematics at St. Petersburg, posted a paper on the www.arxiv.org Web server that is widely used by physicists and mathematicians as a clearinghouse of new research. The paper did not mention the Poincaré conjecture by name, but topology experts who looked at it immediately realized the paper’s relevance to that theorem. Perelman followed up with a second paper in March 2003, and from April to May that year he visited the U.S. to give a series of seminars on his results at the Massachusetts Institute of Technology and Stony Brook University. Teams of mathematicians at nearly a dozen leading institutes began poring over his papers, verifying their every detail and looking for errors.
At Stony Brook, Perelman gave two weeks of formal and informal lectures, talking from three to six hours a day. “He answered every question that arose, and he was very clear,” says mathematician Michael Anderson of Stony Brook. “No one has yet raised any serious doubts.” One more comparatively minor step has to be proved to complete the result, Anderson says, “but there are no real doubts about the validity of this final piece.” The first paper contains the fundamental ideas and is pretty well accepted as being verified. The second paper contains applications and more technical arguments; its verification has not reached the level of confidence achieved for the first paper.
The Poincaré conjecture has a $1-million reward on offer for its proof: it is one of seven such “Millennium Problems” singled out in 2000 by the Clay Mathematics Institute in Cambridge, Mass. Perelman’s proof has to be published and withstand two years of scrutiny before he becomes eligible for the prize. (The institute might well decide that its posting on the Web server qualifies as “published” because the result is undergoing as rigorous a peer review as any paper gets.)
Perelman’s work extends and completes a program of research that Richard S. Hamilton of Columbia University explored in the 1990s. The Clay Institute recognized Hamilton’s work with a research award in late 2003. Perelman’s calculations and analysis blow away several roadblocks that Hamilton ran into and could not overcome.
If, as everyone expects, Perelman’s proof is correct, it actually completes a much larger body of work than the Poincaré conjecture. Launched by William P. Thurston—now at Cornell University—the Thurston geometrization conjecture provides a full classification of all possible 3-manifolds. The 3-sphere, unique in its sublime simplicity, anchors the foundation of this magnificent classification. Had the Poincaré conjecture been false—that is, if there were many spaces as “simple” as a sphere—the classification of 3-manifolds would have exploded into something infinitely more complicated than that proposed by Thurston. Instead, with Perelman’s and Thurston’s results, we now have a complete catalogue of all the possible shapes that a three-dimensional space can take on—all the shapes allowed by mathematics that our universe (considering just space and not time) could have.
Rubber Doughnuts
To understand the Poincaré conjecture and Perelman’s proof in greater depth, you have to know something about topology. In that branch of mathematics the exact shape of an object is irrelevant, as if it were made of play dough that you could stretch, compress and bend to any extent. But why should we care about objects or spaces made of imaginary play dough? The reason relates to the fact that the exact shape of an object—the distance from one point on it to another—is a level of structure, which is called the geometry of the object. By considering a play-dough object, topologists discover which properties of the object are so fundamental that they exist independently of its geometric structure. Studying topology is like discovering which properties humans have in general by considering the properties of a “playdough person” who can be morphed into any particular human being.
If you have read any popular account of topology, you have probably encountered the hoary old truism that a cup and a doughnut are indistinguishable to a topologist. (The saying refers to a ring-shaped doughnut, not the solid, jam-filled kind.) The point is that you can morph the play-dough cup into a doughnut shape simply by smushing the clay around, without having to cut out any holes or glue any patches together. A ball, on the other hand, can be turned into a doughnut only by either boring a hole through its middle or stretching it into a cylinder and gluing the ends together. Because such cutting or gluing is needed, a ball is not the same as a doughnut to a topologist.
What interests topologists most are the surfaces of the ball and the doughnut, so instead of imagining a solid we should imagine a balloon in both cases. The topologies are still distinct—the spherical balloon cannot be morphed into the ring-shaped balloon, which is called a torus. Topologically, then, a sphere and a torus are distinct entities. Early topologists set out to discover how many other topologically distinct entities exist and how they could be characterized. For two-dimensional objects, which are also called surfaces, the answer is neat and tidy: it all boils down to how many “handles” a surface has.
By the end of the 19th century, mathematicians understood how to classify surfaces. Out of all the surfaces, the sphere, they knew, had a unique simplicity. Naturally they started wondering about three-dimensional manifolds. To start with, was the 3-sphere unique in its simplicity, analogous to the 2-sphere? The century-long history that follows from that elementary question is littered with false steps and false proofs.
Henri Poincaré tackled this question head-on. He was one of the two foremost mathematicians who were active at the turn of the 20th century (the other being David Hilbert). Poincaré has been called the last universalist—he was at ease in all branches of mathematics, both pure and applied. In addition to advancing numerous areas of mathematics, he contributed to the theories of celestial mechanics and electromagnetism as well as to the philosophy of science (about which he wrote several widely read popular books).
Poincaré largely created the branch of mathematics called algebraic topology. Around 1900, using techniques from that field, he formulated a measure of an object’s topology, called homotopy. To determine a manifold’s homotopy, imagine that you embed a closed loop in the manifold. The loop can be wound around the manifold in any possible fashion. We then ask, Can the loop always be shrunk down to a point, just by moving it around, without ever lifting a piece of it out of the manifold? On a torus the answer is no. If the loop runs around the circumference of the torus, it cannot be shrunk to a point—it gets caught on the inner ring of the doughnut. Homotopy is a measure of all the different ways a loop can get caught.
On an n-sphere, no matter how convoluted a path the loop takes, it can always be untangled and shrunk to a point. (The loop is allowed to pass through itself during these manipulations.) Poincaré speculated that the only 3-manifold on which every possible loop can be shrunk to a point was the 3-sphere itself, but he could not prove it. In due course this proposal became known as the Poincaré conjecture. Over the decades, many people have announced proofs of the conjecture, only to be proved wrong. (For clarity, here and throughout I ignore two complications: so-called nonorientable manifolds and manifolds with edges. For example, the Möbius band, a ribbon that is twisted and joined in a loop, is nonorientable. A sphere with a disk cut out from it has an edge. The Möbius band also has an edge.)

Geometrization
Perelman's proof is the first to withstand close scrutiny. His approach to analyzing three-dimensional manifolds is related to a procedure called geometrization. Geometry relates to the actual shape of an object or manifold: for geometry, an object is made not of play dough but of ceramic. A cup, for example, has a different geometry than a doughnut; its surface curves in different ways. It is said that the cup and the doughnut are two examples of a topological torus (provided the cup has one handle) to which different geometries have been assigned.
To gain a sense of how geometrization served to help Perelman, consider how geometry can be used to classify 2-manifolds, or surfaces. Each topological surface is assigned a special, unique geometry: the one for which the curvature of the surface is spread completely evenly about the manifold. For the sphere, that unique geometry is the perfectly spherical sphere. An eggshell shape is another possible geometry for a topological sphere, but it does not have curvature evenly spread throughout: the small end of the egg is more curved than the big end.
The 2-manifolds form three geometric types. The sphere has what is called positive curvature, the shape of a hilltop. The geometrized torus is flat; it has zero curvature, like a plain. All the other manifolds, with two or more handles, have negative curvature. Negative curvature is like the shape of a mountain pass or a saddle: going from front to back, a saddle curves up; from left to right, it curves down. Poincaré (who else?), along with Paul Koebe and Felix Klein (after whom the Klein bottle is named), contributed to this geometric classification, or geometrization, of 2-manifolds.
It is natural to try to apply similar methods to 3-manifolds. Is it possible to find unique geometries for each topological 3-manifold, for which curvature is spread evenly throughout the manifold?
It turns out that 3-manifolds are far more complicated than 2-manifolds. Most 3-manifolds cannot be assigned a uniform geometry. Instead they have to be cut up into pieces, each piece having a different canonical geometry. Furthermore, instead of three basic geometries, as with 2-manifolds, the 3-manifold pieces can take any of eight canonical geometries. The cutting up of each 3-manifold is somewhat analogous to the factorization of a number into a unique product of prime factors.


This classification scheme was first conjectured by Thurston in the late 1970s. He and his colleagues proved large swaths of the conjecture, but crucial points that the entire system depended on remained beyond their grasp, including the part that embodied the Poincaré conjecture. Was the 3-sphere unique? An answer to that question and completion of the Thurston program have come only with Perelman’s papers.
How might we try to geometrize a manifold—that is, give it a uniform curvature throughout? One way is to start with some arbitrary geometry, perhaps like an eggshell shape with various lumps and indentations, and then smooth out all the irregularities. Hamilton began such a program of analysis for 3-manifolds in the early 1990s, using an equation called the Ricci flow (named after mathematician Gregorio Ricci-Curbastro), which has some similarities to the equation that governs the flow of heat. In a body with hot and cold spots, heat naturally flows from the warmer regions to the cooler ones, until the temperature is uniform everywhere. The Ricci flow equation has a similar effect on curvature, morphing a manifold to even out all the bumps and hollows. If you began with an egg, it would gradually become perfectly spherical.
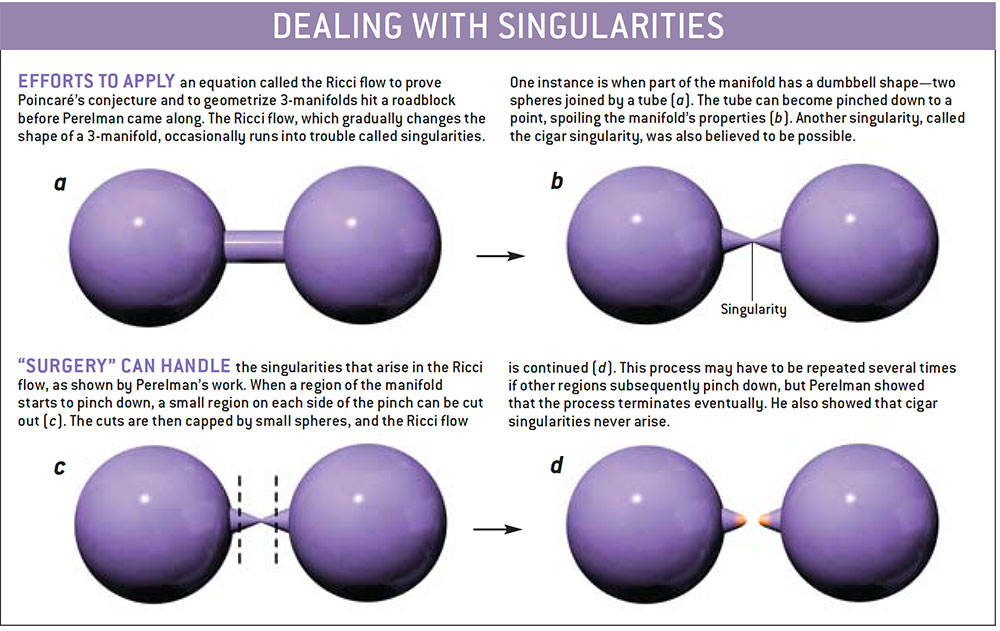
Hamilton’s analysis ran into a stumbling block: in certain situations the Ricci flow would cause a manifold to pinch down to a point. (This is one way that the Ricci flow differs from heat flow. The places that are pinched are like points that manage to acquire infinite temperature.) One example was when the manifold had a dumbbell shape, like two spheres connected by a thin neck. The spheres would grow, in effect drawing material from the neck, which would taper to a point in the middle. Another possible example arose when a thin rod stuck out from the manifold; the Ricci flow might produce a trouble called a cigar singularity. When a manifold is pinched in this way, it is called singular—it is no longer a true three-dimensional manifold. In a true three-dimensional manifold, a small region around any point looks like a small region of ordinary three-dimensional space, but this property fails at pinched points. A way around this stumbling block had to wait for Perelman.
Perelman came to the U.S. as a postdoctoral student in 1992, spending semesters at New York University and Stony Brook, followed by two years at the University of California at Berkeley. He quickly made a name for himself as a brilliant young star, proving many important and deep results in a particular branch of geometry. He was awarded a prize from the European Mathematical Society (which he declined) and received a prestigious invitation to address the International Congress of Mathematicians (which he accepted). In spring 1995 he was offered positions at a number of outstanding mathematics departments, but he turned them all down to return to his home in St. Petersburg. “Culturally, he is very Russian,” commented one American colleague. “He’s very unmaterialistic.”
Back in St. Petersburg, he essentially disappeared from mathematicians’ radar screens. The only signs of activity, after many years, were rare occasions when he e-mailed former colleagues, for example, to point out errors in papers they had posted on the Internet. E-mails inquiring about his pursuits went unanswered.
Finally, in late 2002 several people received an e-mail from him alerting them to the paper he had posted on the mathematics server—just a characteristically brief note saying they might find it of interest. That understatement heralded the first stage of his attack on the Poincaré conjecture. In the preprint, along with his Steklov Institute affiliation, Perelman acknowledged support in the form of money he had saved from his U.S. postdoctoral positions.
In his paper, Perelman added a new term to the Ricci flow equation. The modified equation did not eliminate the troubles with singularities, but it enabled Perelman to carry the analysis much further. With the dumbbell singularities he showed that “surgery” could be performed: Snip the thin tube on each side of the incipient pinch and seal off the open tube on each dumbbell ball with a spherical cap. Then the Ricci flow could be continued with the surgically altered manifold until the next pinch, for which the same procedure could be applied. He also showed that cigar singularities could not occur. In this way, any 3-manifold could be reduced to a collection of pieces, each having a uniform geometry.
When the Ricci flow and the surgery are applied to all possible 3-manifolds, any manifold that is as “simple” as a 3-sphere (technically, that has the same homotopy as a 3-sphere) necessarily ends up with the same uniform geometry as a 3-sphere. That result means that topologically, the manifold in question is a 3-sphere. Rephrasing that, the 3-sphere is unique.
Beyond proving Poincaré’s conjecture, Perelman’s research is important for the innovative techniques of analysis it has introduced. Already mathematicians are posting papers that build on his work or apply his techniques to other problems. In addition, the mathematics has curious connections to physics. The Ricci flow used by Hamilton and Perelman is related to something called the renormalization group, which specifies how interactions change in strength depending on the energy of a collision. For example, at low energies the electromagnetic interaction has a strength characterized by the number 0.0073 (about 1⁄137). If two electrons collide head-on at nearly the speed of light, however, the strength is closer to 0.0078.
Increasing the collision energy is equivalent to studying the force at a shorter distance scale. The renormalization group is therefore like a microscope with a magnification that can be turned up or down to examine a process at finer or coarser detail. Similarly, the Ricci flow is like a microscope for looking at a manifold at a chosen magnification. Bumps and hollows visible at one magnification disappear at another. Physicists expect that on a scale of about 10–35 meter, or the Planck length, the space in which we live will look very different—like a “foam” with many loops and handles and other topological structures. The mathematics that describes how the physical forces change is very similar to that which describes geometrization of a manifold.
Another connection to physics is that the equations of general relativity, which describe the workings of gravity and the large-scale structure of the universe, are closely related to the Ricci flow equation. Furthermore, the term that Perelman added to the basic flow used by Hamilton arises in string theory, which is a quantum theory of gravity. It remains to be seen if his techniques will reveal interesting new information about general relativity or string theory. If that is the case, Perelman will have taught us not only about the shapes of abstract 3-spaces but also about the shape of the particular space in which we live.
--Originally published: Scientific American 291(1); 94-103 (July 2004).