
A Counting Primer
Pins, forks, and removal of the guard tactics usually occur several times during a game. Counting takes place whenever exchanges are possible – almost every move after the early opening.
Tactics can be considered the science of piece safety, with the goal of winning material or mating. Recognizing an opponent’s tactics is equally important so that one can prevent losing material or mate. Thus, at the start of a game, defense is just as important as offense. One can approximately divide all tactics, in increasing order of average complexity, into five levels:
1. En Prise – an unguarded piece that can be captured.
2. Counting – determining whether any series of captures might lead to losing material.
3. Single Motif – pins, double attacks, back-rank mates, removal of the guard, etc.
4. Non-sacrificial Combinations – combines motifs (including counting).
5. Sacrificial Combinations – Same as #4, but it involves a sacrifice.
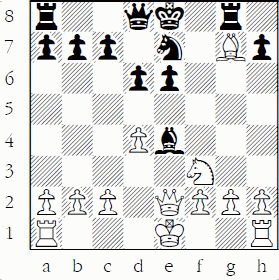
En prise is the easiest to understand. Here is a simple example, after 1.d4 Nf6 2.e4?:
Black to play

The white e-pawn has been placed en prise and Black can – and should – capture it safely with 2...Nxe4.
Counting: The process of determining whether each piece, for both sides, is safe on each move (using only the nonglobal “on its square” definition).
Most beginner’s books bypass counting and immediately delve into single motif tactics: pins, double attacks, removal of the guard, etc. Yet, players rated under 1400 (below the average adult tournament player) are very susceptible to making counting errors that cost them games. These errors may occur because they misunderstand the value of the pieces, but often they just miscalculate. Hence, we begin with this important chapter on safety and counting!
Counting is the process of determining whether any series of captures might lead to losing material, if it doesn’t then the piece can be captured “safely” – at least safe from losing material because of counting. Much more on this below!
The Average Value of the Pieces
Many players learn the following set of average piece values:
Pawn = 1 pawn (not points!)
Knight = 3 pawns
Bishop = 3 pawns
Rook = 5 pawns
Queen = 9 pawns
I call these Reinfeld values because many of the beginner chess books in the 1950’s and 1960’s were written by Fred Reinfeld and included these values. They can be used to solve most of the “play and win” problems in this book, because if you find the correct sequence, then you should finish the problem ahead in material and any reasonable set of values is acceptable. Reinfeld values are very easy to teach beginners, but if you are going to be a good player you are going to have to graduate from them or at least not adhere to them slavishly.
Note that Reinfeld’s numbers cannot be exact, if for no other reason than the average value of every piece cannot be an exact integer multiple of the value of a pawn. That would be like saying every human being is exactly an integer multiple of one foot tall, and has to be exactly 5 or 6 feet in height.
In 1999, Larry Kaufman wrote an award-winning article in Chess Life on piece value, based on a scientific computer study of about 80,000,000 positions! To summarize Larry’s findings, the best average piece values (rounded to quarters) are:
Pawn = 1 pawn
Knight and Bishop = 3¼ pawns
Rook = 5 pawns
Queen = 9¾ pawns
Larry also found that having the advantage of the bishop-pair (when you have both bishops and your opponent does not) is worth a bonus of about a ½ pawn. Additionally, while the king has infinite value, the fighting value of a king – usually seen in the endgame – is about 4 pawns. These are important ideas to remember and use!
An easy way to use Larry’s values is to consider the exchange (winning a rook for a bishop or a knight) as worth about ½ a piece (a “piece” in this context always means a bishop or knight). This is quite a bit different than the Reinfeld value, which places the exchange’s value at about two-thirds of a piece. That is a big difference in percentage!
Another way to evaluate material in terms of a rook is that the exchange is worth about one-third of a rook; a piece is worth about two-thirds of a rook; a queen is worth about two rooks; and, of course, a rook is worth one rook.
These average values are great starting points for players above beginner level and can be extremely helpful in many “normal” situations. The actual value of a piece is determined by how powerful it is in a given position and is a much more complex subject!
Checks, Captures, and Threats
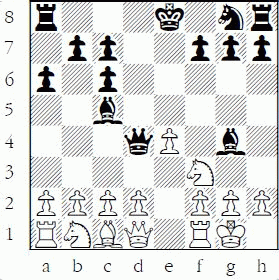
A capture is when a piece moves and takes an opponent’s piece off the board. A threat is a move that can do something positive, if not countered, on your next move, such as win material or checkmate. If you make a move that threatens to capture an opponent’s piece on your next move, that is called an attack. An attack on a king, of course, is called a check.
The list of forcing moves is a mantra I give to my students: look for checks, captures, and threats! It is important to note that not all attacks are threats. For example, in the diagram below, the black queen attacks the knight on a4, but it is not a threat since Black would then lose his queen to Qxa4.

Safety and Counting Definitions
Some players think that counting is simply knowing the value of the pieces and understanding, for example, not to trade a rook for a bishop because a rook is worth more.
Safe: A piece is safe if no possible sequence of exchanges on the square it occupies will lose material, assuming best play by both sides moves.
The definition at right will clarify when a piece is safe with regards to exchanges on its square. Here “piece” includes pawns, but not kings, which are special with regard to safety issues. This definition will subsequently allow me to present one for counting. We need to assume best moves in our definition because you can always lose material on any capture just by playing poorly and refusing to recapture! In that case every attacked piece would be unsafe, which is clearly not true.
As a simple example of safety, suppose you can trade pawns, then both side’s pawns are safe because it is a fair trade and no one loses material. It is very important to note that if we expand our definition to the entire board, and not just a square, then the global definition of safe would involve all tactics, and not just exchanges on a particular square.
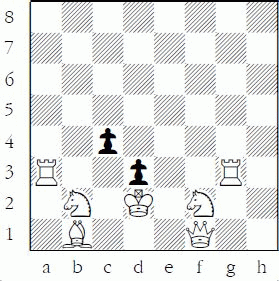
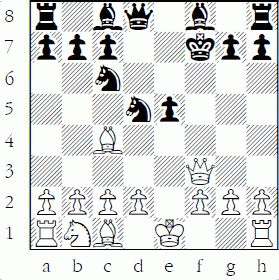
With White to move in the following diagram, the black bishop on b4 is not attacked, so from just a counting standpoint the bishop is safe but, of course, White can play the double-attack 1.Qa4+, and thus the bishop is not safe from a tactic. If it were Black to move in the same diagram, then the knight on c3 is not safe even just by counting since it is defended once, but Black could capture twice and win a pawn.

So, considering the entire board, we must expand our definition of safe, as shown below.
Safe (global): A piece is safe if no tactic by the opponent involving the capture of that piece can forcibly win material (including counting!).
Counting: The process of determining whether eachpiece, for bothsides, is safe on eachmove (using only the non-global “on its square” definition).
However, identifying all the ramifications of this global definition of safe is a very complex topic – and well beyond the scope of this book! So back to counting.
To determine safety, you do not have to count on each square on each move! This is an important practical consideration!
Most advanced players have a subconscious “important squares database” that consists of whether or not all attacked squares are adequately guarded. They update this database on each move: only the squares affected by the move are recalculated. If everything was safe on the previous move, then one need only look at the affected squares of the next move to determine if something has become unsafe. Therefore, stronger players don’t often leave pieces “hanging” from one move to the next. This process becomes routine with adequate practice. Note that if one uses the global definition that includes all tactics, then a more detailed analysis is needed to ensure all your pieces are safe.
There is a fine line between the tactical motif removal of the guard (see Section 2.7) and its simpler cousin, counting. Removal of the guard involves captures on multiple squares so that a defender is captured or has to move and the defended piece is no longer safe. However, the distinction between the two concepts is somewhat tricky because safety has to be determined on all squares each move, so multiple squares are often involved even on purely counting issues. The difference is that, with removal of the guard, the safety on one square is directly dependent on the removal of the defender from another square, while in regular counting the safety of each of the multiple squares is determined independently. Confused? Don’t worry, clear examples lie ahead!
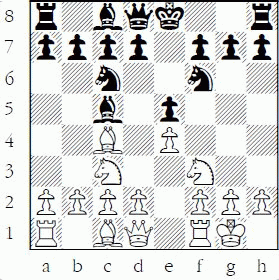
In the diagram below, the rook on e6 is not safe because White can play 1. Bxe6 and win the exchange (rook for bishop) provided Black recaptures. White does not have to continue with 2.Qxe6?? losing material; chess is not checkers – you don’t have to capture!
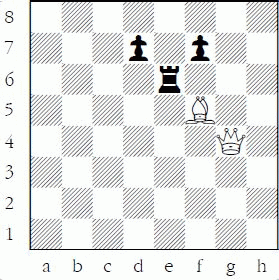
Contrast this diagram to a removal of the guard example in the next diagram. Through simple counting, both knights appear to be safe: 1.Bxe6 dxe6 is a trade of bishop for knight, both roughly worth the same (3¼ pawns), and 1.Rxc6 dxc6 would seem to lose the exchange for White.

However, when we combine these two exchanges, we can easily see that the d7-pawn is overworked. Overworked pieces that guard attacked pieces leads to a removal of the guard tactic. White should play 1.Bxe6
If Black does not recapture, White remains ahead a knight. But if Black plays 1...dxe6 then White plays 2.Rxc6 since the knight on c6 is no longer guarded and White still wins a knight. Thus the safety of each black knight is interrelated, making this a removal of the guard problem, and not just a simple counting issue. Note that the opposite move order, starting with 1.Rxc6, while still winning material, is not as good. After 1...dxc6 2.Bxe6 White has won only two pieces for a rook, which is not nearly as favorable as winning a piece. I calculated that result by counting the traded material, but this is not a counting problem – see the difference? See Chapter 2.7 for more about removal of the guard tactics.
If you use Larry Kaufman’s values (henceforth just “the value” of a piece), then trading a knight and bishop for a rook and a pawn loses about half a pawn worth of material. However, if in doing so you also lose the bishop-pair, you lose a total of about 1 pawn, which is approximately what it takes for one master to beat another!
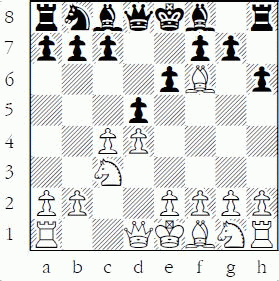
The following common beginner sequence involves counting on f7, and is a terrific example of how to calculate material. If you understand this example, you understand a lot about material value: 1.e4 e5 2.Nf3 Nc6 3.Bc4 Bc5 4.O-O Nf6 5.Ng5?! O-O 6.Nxf7? Rxf7 7.Bxf7+ Kxf7 (D)
A beginner playing white might misevaluate the position: “I have given up a bishop and knight for a rook and pawn – so each side has traded six pawns, but his king is exposed, so I am winning.”
White to play after 7...Kxf7
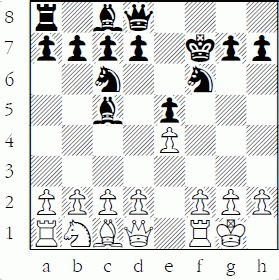
While an experienced player with the black pieces should evaluate: “White has given up a bishop and knight for a rook and pawn, so I am ahead about half a pawn (6½-6), but I also have the bishop pair, so that is worth about an extra half pawn, making it one pawn ahead, and finally I am ahead about 3 tempi, which is worth nearly another pawn, for a total of almost two pawns ahead. My king is also safer than his because I can get my pieces headed for his king quicker than he can get at mine, so I am pretty much winning.”
This situation has resulted entirely because of White’s initial “counting error” that encouraged him to attack and then trade on f7, as well as his misunderstanding of other aspects of the position.
A similar mistake in using the Reinfeld values is believing that winning the exchange is worth two full pawns when, in fact, the exchange is only worth about half a piece, and even less if you lose the bishop-pair. Getting a pawn and the bishop-pair is almost worth the exchange and in many positions is worth more. Weaker players often overrate the exchange.
Moreover, it is amazing how many players think they are losing a rook when they are really only losing the exchange! This is an enormous 3+ pawn counting error that I continually see. Many times I have watched a beginner voluntarily lose a piece (!) instead of the exchange because “he did not want to lose a ‘rook’!” So it is worth repeating: It is much better to lose a rook for a piece (the exchange), than a piece for nothing! As noted above, it is only about half as bad to lose the exchange as to lose a piece.
A student reached the position in the diagram below while playing Black on the Internet. A few moves before Black had been ahead three pawns and was winning easily. He should have heeded my advice on how to play when you are way ahead, such as think defense first (but don’t play defensively) and keep things simple. Instead, he needlessly met an attack with a counterattack, the position got a little complex, and now he had to lose material.
Black to play
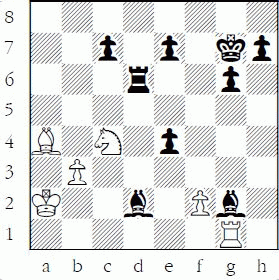
The good news was that if he played carefully he would still likely have an “easy” win. After the “routine” 1...Bf3! 2.Nxd6 exd6 he has the bishop-pair and three pawns for the exchange. Instead he hesitated – you could almost hear him incorrectly thinking “don’t lose the rook!” – and he played 1...Rd3?? saving the exchange instead of the piece! After 2.Rxg2 he had a very bad position and soon lost on time.
The next diagram illustrates a very common beginner counting mistake. Black has just played 1...h6 and attacked the knight. White, as often is the case, should just retreat the knight, but many beginners unnecessarily complicate things by counterattacking the rook with 2.Bh3? or 2.Ba6?.
White to play

If 2.Bh3?, then 2...Rc3 hits the bishop, which is temporarily guarded by the knight, but the knight must move! Thus Black would win a piece by this self-destructive removal of the guard.
If 2.Ba6?, then 2...Ra8 again attacks the bishop. Since the knight cannot move and guard the attacked bishop, White must try 3.Bb7, again attacking the rook, but then 3...Ra7 or 3...Rb8 attacks the bishop once more and, with two pieces attacked, White must again lose a piece!
If we begin, say, with a king at b8 guarding the rook on c8, then the error is even more egregious!
White to play
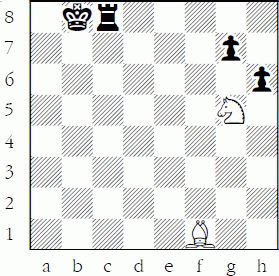
Now 2.Ba6? or 2.Bh3? is even sillier, since White should see that even if Black simply settles for 2...hxg5, winning a piece, then 3.Bxc8 Kxc8 just wins back the exchange – not a rook! – and White remains down two pieces for a rook. But if White does play 2.Ba6 or 2.Bh3, Black should follow the important guideline: when you see a good move, look for a better one, and win an entire piece as in the previous diagram.
The following diagram is an advanced example of an exchange sacrifice that is routinely played by strong players, but usually not even considered by weak players:
Black to play
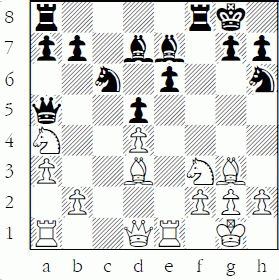
The position is from Keres-Bronstein, Moscow 1956. Bronstein continued 18...Rxf3! 19.gxf3 Nxd4 and Black was a little better, not “down a pawn” as a Reinfeld “rook is worth 5, knight plus pawn is worth 4” evaluation would have you believe.
Five Ways to Save an Unsafe Piece
There are five ways to save an unsafe piece:
1. Move it to a safe square.
2. Capture the attacking piece.
3. Block the attack by putting another piece in the line of attack. This is known as interposition and only works against long-range attacks by bishops, rooks, and queens.
4. Guard the piece.
5. Counterattack (includes pinning the attacking piece,
Each of the five ways to save an unsafe piece has pros and cons and usually only one way is best, and that has to found by analyzing. Let’s look at each method:
Moving to a safe square is often the easiest. Of course, if your piece cannot move at all (as pawns often cannot), then this option is not available.
Capturing the attacking piece is often the best option when it is possible. Occasionally, I see beginners make the following enormous double-blunder:
White to play
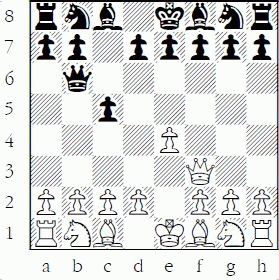
White does not count correctly and plays 1.Qxf7+?? Black, of course, should take the queen with 1...Kxf7, but young beginners often automatically “move their king out of check” instead of looking at the other possibilities of capturing the checking piece or blocking the check. So they play 1...Kd8?? and just lose a pawn! And with the black queen on d8, they often “resign,” since they assume 1.Qxf7+?? is checkmate!
Blocking the attack can create a pin (see Chapter 2.2), but it is often a good way to get out of check early in the game to retain the right to castle.
Guarding the piece is passive and may lead to a removal of the guard tactic (see Chapter 2.7). Also, guarding with something other than a pawn often ties down a piece of greater value that would rather be doing something else!
A counterattack is by far the trickiest method, because if you are way ahead in material, you don’t want complications. If you counterattack an opponent’s piece in response to an attack, then you might be faced with a double attack that you cannot meet:
White to play
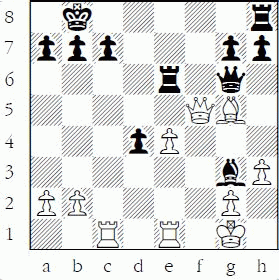
White is already in difficulty and his rook on e1 is attacked. Instead of simply moving his rook, White counterattacked with 1.Qxg6? and this counting error allowed Black to recapture with 1...Rxg6 attacking the bishop, too. White cannot now save both his bishop and rook. My weaker students make this kind of mistake with great frequency; therefore, it is a good one to understand and avoid!
It only takes one bad move to lose a game. So be careful on every move!
Counting Exercises
These exercises can enhance a player’s ability to see whether a trade of pieces is favorable. I suggest that any beginner start with these before attempting more advanced tactical exercises. Adequate counting is a prerequisite for tactical problems such as pins, double attacks, and removal of the guard. These exercises start out very simple, but I think most readers will learn something!
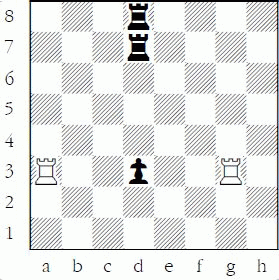
Each of the next nine problems poses the question, “White to move: is the black pawn on d3 safe?” The kings aren’t included so that you don’t try other moves – we are just concentrating on captures on d3, concentrating only on the safety of the pawn on that square.
White to move: is the black pawn safe?
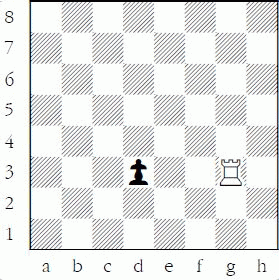
The answer is, of course, no. 1.Rxd3 would win the pawn. Too easy, you say? True, but let’s increase the difficulty one step at a time. Since the pawn is attacked once and is guarded zero times, you can win it. This represents the first level of safety, en prise since the pawn can be freely taken. En prise involves counting in a trivial sense, where the attacker’s count is one or more and the defender’s count is 0!
White to move: is the black pawn safe?

Now the answer is yes, the pawn is safe. After 1.Rxd3? Rxd3 Black would be ahead by about four pawns: (rook=5) – (pawn=1) = 4. Therefore, White, with the freedom to make any move he wants, would almost undoubtedly not take the pawn. We can see from this example that if a piece or pawn is guarded as many times as it is attacked, it is safe from capture as long as all the guarding pieces have the same value as the attacking pieces (which, as we shall see shortly, is not always the case!).
White to move: is the black pawn safe?

Now the answer is again no. After 1.Raxd3 Rxd3 (not recapturing also leaves Black a pawn behind) 2.Rxd3, White wins a pawn, so it is not safe. Notice here the pawn is attacked twice and defended once, all by pieces of the same value, so that is an indication that it is not safe.
White to move: is the black pawn safe?
When the game gets complicated and there are many checks and captures, it is usually correct to make a check or capture, or at least an extremely strong threat, to hold the initiative. To make a quiet move in violent positions usually gives your opponent the opportunity to take the initiative.
Yes, here it is safe. After 1.Raxd3? Rxd3 2.Rxd3 (not recapturing still does not help White) 2...Rxd3, Black is again ahead four pawns.
White to move: is the black pawn safe?
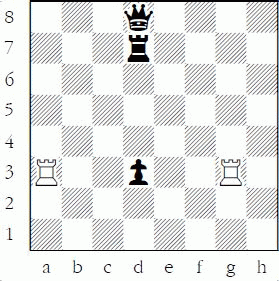
The answer is still yes, the pawn is safe. Substituting a queen for the black rook behind the pawn makes no difference, because the queen can capture last. After 1.Raxd3? Rxd3 2.Rxd3 Qxd3, Black is again ahead four pawns. But with just a simple switch...
White to move: is the black pawn safe?
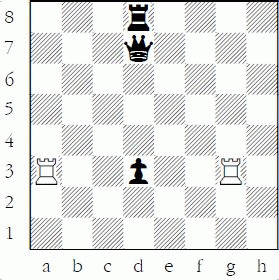
Suddenly the problem isn’t so trivial! With the queen in front of the black rook, any recapture gives up the queen: After 1.Raxd3 Qxd3 2.Rxd3 Rxd3, Black has captured two rooks (2 x 5 = 10), but had to give up a pawn and a queen (9¾ + 1 = 10¾), so the trade is just slightly better for White, although the answer depends to a large extent on where the rest of the pieces are since the “Kaufman” values I used are just averages! In this case the pawn is often considered safe (since the queen value may vary so much by position), but a valuable lesson is learned – it matters what order you can capture (or recapture) when determining whether a piece is safe.
It matters what order you can capture (or re-capture) when determining whether a piece is safe.
White to move: is the black pawn safe?
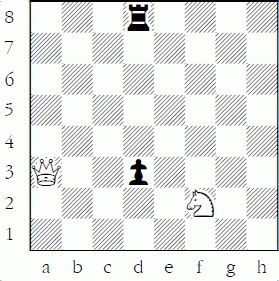
The above example shows that the attacker’s capturing sequence also matters. The pawn is not safe as long as White properly captures with his lowest valued piece: 1.Nxd3 wins the pawn. Notice that Black would be foolish to recapture, as 1...Rxd3 2.Qxd3 wins the pawn and the exchange. In that case White captures 5+1 = 6; Black captures 3¼, so Black loses 2¾ instead of the 1 he would have lost if he had not recaptured. Remember, you are never forced to recapture! Young beginners often make the mistake of making all possible captures on a square once one has been initiated. Of course, if White had captured with the queen first, that would be a huge mistake, as after 1.Qxd3? Rxd3 2.Nxd3, White would lose the equivalent of 3¾ pawns – a queen (9¾) for a rook and pawn (5+1).
In the next diagram, all of White’s pieces are ready to capture Black’s pawn on d3, but it is safe no matter how many times it is attacked by higher valued pieces, because the combined value of the defending piece (the pawn at c4) and the attacked piece (the pawn at d3) is less than the value of any piece that can take it.
White to move: is the black d3-pawn safe?
So any capture on d3, such as 1.Nbxd3? cxd3 2.Nxd3 will cost White the equivalent of 3¼ pawns (a knight) while winning only two, a net loss of 1¼. Of course, White can capture the unguarded pawn on c4 with 1.Nxc4, but that was not the question!
White to move: is the black pawn safe?
This very important example shows that you just cannot count up the value of all the pieces that would be capturing on the square (except one never counts the final piece, which captures last and is not taken off the board). White should play 1.Bxd3, and if Black plays 1...Qxd3?, then White should play 2.Rxd3 Rxd3 and then White should not recapture, but instead move his queen to safety, coming out about 2½ pawns ahead (getting 1+9¾ = 10¾ and giving up 3¼+5 = 8¼). If White continues 3.Qxd3? Rxd3, then White would have given up 3¼+5+9¾ = 18 and only gotten 1+9¾+5 = 15¾, losing 2¼ pawns instead! So the pawn is not safe. This illustrates that you should only do as much exchanging as is favorable to you; any further exchanges that are unfavorable are not forced and should be avoided.
No Fractions!
Although I did the “math” for you in the problems above, good players rarely count up the value of the pieces in a trade – and they rarely think in fractions! That would make chess too hard and less fun. Instead they just compare what was taken off the board or what is left on! For example, if they win a queen and a pawn for a rook and a bishop they know this is a good deal unless something special is happening with the remaining pieces. Or they just see that a certain trade, such as a giving up a bishop and knight for a rook and pawn, is favorable or unfavorable in a particular position. So don’t worry about the fractions!
Just remember what we stated above: the exchange is worth about half of a piece or about one-third of a rook, and a piece is worth about two-thirds of a rook (or, “a little less than two pawns less than a rook”). A queen is usually worth a little less than two rooks, but at least a pawn more than a piece and a rook. Even if you just remember that a knight or bishop, on the average, are worth about the same, and a little more than three pawns, that goes a long way!
If the count is so close that fractions are important, then it is likely that the other factors become important as well and it’s still probably not necessary to calculate the fractions. As noted earlier, using the easier Reinfeld numbers is perfectly acceptable for all but the closest counting problems. The answers in the examples below are based on the Kaufman values.
Queen’s Gambit Counting
Now that we have “counted out” the pawn on d3, let’s consider a more practical example – the safety of the black pawn on d5 in the Queen’s Gambit. After 1.d4 d5 2.c4 White initiates a series of attacks on d5 and Black responds.
Black to play
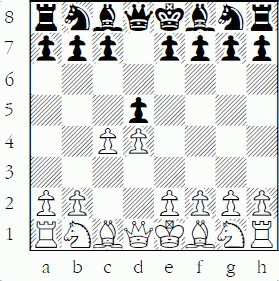
White has the threat of 3.cxd5 Qxd5 4.Nc3 hitting the queen with tempo, so Black’s three main moves are 2...dxc4 (Queen’s Gambit Accepted), 2...c6 (Slav), and 2...e6 (Queen’s Gambit Declined). Assume that Black chooses the latter and then White increases the pressure on d5 with 3.Nc3.
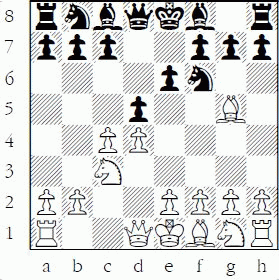
Black to play

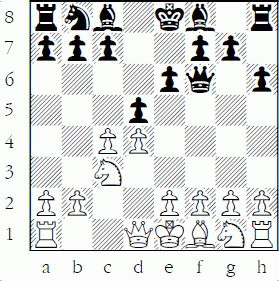
If we count, we can see that White is still not threatening d5, because if Black ignores d5 and plays 3...h6?, White still cannot play 4.cxd5 exd5 5.Nxd5?? as he loses a piece to 5.Qxd5. Nevertheless, Black has a good plan to “overprotect” his d5-square with 3...Nf6. Now the most common move for White is to pin the protector with 4.Bg5.
Black to play
In this position White resumes his threats, as 4...h6? is met by 5.Bxf6. Now further counting reveals Black has some problems:
Black to play
Black must recapture the bishop on f6 (counting tells us if he plays 5...Qd7??, then White retreats the bishop and is ahead a piece), but both ways to recapture have drawbacks. If 5...Qxf6, then counting tells us that d5 is now attacked twice and defended only once:
White to play
So White can play 6.cxd5 exd5 7.Nxd5, when something more than counting tells us that he has to also check for 7...Bb4+?, which would win the queen if it weren’t for 8.Nxb4!. But if Black recaptures on f6 with 5...gxf6, White still exchanges pawns on d5 with 6.cxd5 exd5 and Black’s kingside pawn position is somewhat of a mess:
White to play

Therefore, on move four, Black sidesteps all this with 4...Be7 (instead of 4...h6?) so that the queen can continue to guard d5 even if the knight is captured. And the dance continues!
You should only do as much exchanging as is favorable to you.
This kind of counting “joust” forms the basis of the fight for squares in many openings:
As defenders are added and removed from these squares, beginners often lose track of the counting and either lose a pawn or cede strong central control to their opponents. As you get more experienced and more careful with your counting, you will survive the openings much more!
More Complex Counting Examples
If you have a little bit of experience, you might have read all of the above “d3” and “d5” examples and said to yourself: “I didn’t learn anything. These ‘simple’ counting problems would never happen to me.” Unless you are a very strong player, you are almost undoubtedly wrong – such miscounts happen constantly in the games of my students, even the ones I consider to be at an intermediate level. Consider the following counting error that occurred in a slow game of one of my students, who is by no means a weak player. He, too, would have denied making such mistakes, because he was not aware of this one until I pointed it out to him!
Black to play
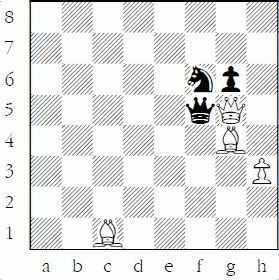
To best illustrate his error I have removed the irrelevant pieces from the position from the above diagram, but material was even in the actual position. White has just played 1.Bg4 attacking the queen:
Black saves the queen by playing 1...Nxg4. What should White do?
White wanted to trade queens and played the “counting error” 2.Qxf5? This zwischenzug allowed Black to recapture 2...gxf5 and then after White captured back with 3.hxg4, Black had an extra attacker on g4 and was able to win a pawn with 3...fxg4. Black, up a pawn, went on to win the endgame. Instead, White should simply have recaptured on g4 with 2.Qxg4 or 2.hxg4, and material would have been even. Even more amazing is my student was unaware that his capturing sequence lost a pawn! Even a good player can lose track during a capturing sequence – so be careful!
Here is another position where an intermediate player had trouble discerning the correct sequence. Black has just played 1...Re2+ and White has to be careful about counting to properly defend.
White to play and not lose material
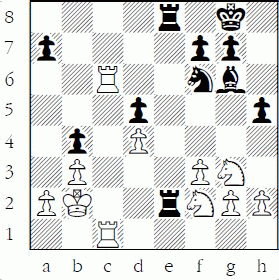
Some of the obvious sequences lose material:
(a) 2.Nxe2 Rxe2 3.Ka1 Rxf2 wins two pieces for a rook.
(b) 2.R1c2 Bxc2 3.Nxe2 Bxb3! wins a pawn.
That leaves only the correct 2.Nxe2 Rxe2+ 3.R1c2 Or 3.R6c2, either way, interposing with a rook is correct, even if it can be taken by the bishop on g6. 3...Bxc2 4.Rxc2 is the correct sequence. Even seemingly simple sequences are easy to miscount!
Counting can be extremely complicated when combined with tactical motifs, especially removal of the guard, since it now becomes part of a multiple-motif calculation. Consider the following example from IM John Watson’s Secrets of Modern Chess Strategy (notes based on Watson’s and the computer program Fritz 9). It is from the game Szabo-van Seters, Hilversum 1947, after Black’s move 16...Rd7:
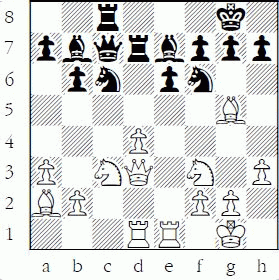
Determining whether White can safely play 17.d5 is difficult. I am not asking whether 17.d5 is a good move – that is even harder! I am “just” asking whether playing 17.d5 forcibly loses material in any line.
The game continued: 17.d5! White activates his central forces. Fritz assesses this as clearly best at 11 ply (half-moves), evaluating White as better by almost a pawn Watson writes: “This pawn-break epitomizes White’s strategy and its payability...” Note his word “payability” – in one sense he means that it is a safe move! 17...Nxd5 Fritz rates this as a mistake, but even after the improvements 17...Qb8 or 17...h6, White is much better. 18.Bxd5! This is superior to the alternative 18.Nxd5. 18...Qd8? Fritz evaluates 18...h6 as the only move that even stands a chance. 19.Qe4 This wins, but Watson doesn’t mention that 19.Bxe7 Nxe7 20.Ng5 is even more advantageous! 19...exd5 Better, but not sufficient to save the game, is 19...Bxg5 20.Bxe6!. 20.Nxd5 It is apparent that White has a massive attack. 20...Bxg5 21.Nxg5 g6 22.Qh4 h5 Now a simple fork with the underrated tactic “removal of the guard” wins the exchange: 23. Nf6+ Qxf6 24.Rxd7 Nd8 25.Re8+ Kg7 26.Rxf7+ 1-0 Fritz does not rate this as one of White’s three best moves, but any move that is sufficient to cause resignation is probably good enough!
It is worthwhile to know how to count correctly and to take care when doing so, because I often see counting errors committed by players of even intermediate tournament strength. Counting is quite an underrated skill and it is difficult to master. All basic chess texts should teach this important task.
A Counting Game
Let’s follow a game where both players had typical and instructive counting difficulties. The time limit for this game was fairly slow, so both players had time to be careful. My student had white.
1.e4 e5 2.Nf3
This attack on e5 introduces our first count of the game; e5 is now attacked once and defended zero times. As defined earlier, the pawn would be considered en prise, but it is Black’s move.
2...Ne7?? (D)
Black neither defends his pawn with the usual 2...Nc6, nor with 2...d6 (Philidor’s Defense), nor counterattacks the white e-pawn with 2...Nf6 (Petroff’s Defense). Therefore, the pawn is truly en prise because now it is White’s move.
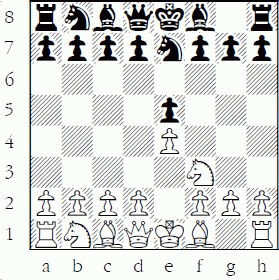
3.d4??
You may chuckle at White missing the “obvious” 3.Nxe5, but I have seen this error dozens of times among beginners. They correctly think, “The main idea of the opening is to mobilize the forces,” but forget that tactics are almost always much more important than activity. Winning material – especially when material is even – is important throughout the game, and not just in one phase. So they erroneously play their intended developing move, without looking to see if there is a tactic. Don’t try to outsmart yourself. If you have a simple move that follows a well-known and important guideline such as, when the position is close to even, win material unless you see a refutation, just follow the guideline and don’t try to make chess harder than it is!
One of the main reasons you mobilize your forces is to be in a better position to win material or to avoid losing it. The two main ways games are won are through mating attacks or by winning material and then eventually mating through attrition (trade pieces when ahead!) – but the latter is more common. So if you can just win material for nothing, it is worth delaying your mobilization for a move!
The most important opening guideline, which is often violated by strong players, is: move every piece (not pawn) once before you move any piece twice – unless there is a tactic for either side. But here the final clause is crucial – you don’t give away material just because you don’t want to move something twice, nor would you forego winning your opponent’s queen just because you have to move a knight twice to capture it. This reasoning is just common sense, but you have to follow it!
A move that looks ridiculously bad at one level just looks normal to an untrained eye at lower levels. I think most players rated 1300 would see 3.d4?? as a terrible move. However, when those same players move a piece to make an easily defendable threat, instead of getting another piece into play, a 1300 player sees that as normal, when any player over 1800 would “see” an easily defendable and otherwise time-wasting threat that was as bad as 3.d4??. The only difference is that, instead of not gaining material, the 1300 player is “just” losing time, but losing anything for nothing is not good!
The general rule is that the “little” things are more important when the game is close to even, and, onversely, the little things are less important the bigger the advantage is. For example, if you were ahead a queen, then stopping to win an ordinary pawn would be unnecessary and likely wasteful because you are already easily far enough ahead to win, and in that case it would be much more important to get all your pieces into the game quickly – then your superior force probably enables you to win all the material you want! Or, when you are ahead a piece, giving yourself an isolated pawn is a very small price to pay if it enables you to trade queens.
But in the above position the game is even, and winning the first pawn is often enough for a strong player to win the game, so in this case it is clearly more important than development. The loss of the pawn after 2...Ne7? is also different than a gambit, where a pawn (or more) is sacrificed to purposely gain development, hopefully enough to compensate for the lost material. In general, at the very start of the game you need to get ahead by two or preferably three tempi for the first pawn you gambit and here, with the knight on e7 blocking Black’s development, Black will probably be lucky to get ahead by one tempo, if at all.
3...exd4 4.Nxd4 d6 5.Be2
5.Bc4 is a more active move. White’s fifth move raises an important question about the weak but still useful guideline “develop knights before bishops.” Does that mean both knights before both bishops, or does it mean the knight on each side before the corresponding bishop? It can mean either, but more often it means the latter, so that you can castle as quickly as possible. So even though 5.Nc3 is a perfectly good move, developing the bishop is not a violation of this principle.
5...Nd7
Black apparently likes cramped positions!
6.Bg5
This does violate the above guideline. While 6.Bg5 is a perfectly good developing move, I would prefer students who are still learning to play 6.O-O or 6.Nc3. After 6.Bg5, it is easy to envision many white players losing the unguarded bishop to a sequence such as 6...c6 7.e3?? Qa5+ because Loose Pieces Drop Off! Note that the attacked knight on e7 is safe since, if Black does nothing, after 7.Bxe7? Bxe7, it is White who loses material, since he just forfeited the advantage of the bishop-pair for nothing!
6...Nc5
An attack on e4; the pawn will be en prise unless White safeguards it.
7.Nd2
This move unnecessarily blocks the queen and subsequently the rooks. The more centralizing 7.Nc3 was better – both moves make the e4-pawn safe. However, when you see a good move, look for a better one.
7...Qd7 8.b4
My criticism of this move is similar to that of 6.Bg5. While it is a relatively advanced idea to use pawns to remove knights from good squares, doing so before you complete your development can be dangerous. The simple 8.O-O was preferable: castle early and often is a humorous aphorism that strikes the point home – castling is such a good move that if you were allowed more moves that get two pieces into play instead of one, you would use them!
The move 8.b4 permanently weakens the squares a3, a4, c3, and c4 since the d-pawn is already gone. It also leads to a trivial example of counting. White is threatening to trade a pawn for a knight on c5, and since the knight is worth more, it is not safe!
8...Ne6
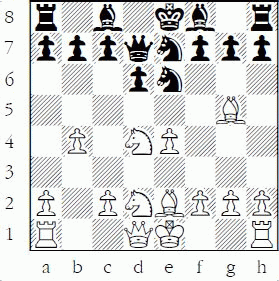
A double attack on d4 and g5, both containing unguarded pieces; White has to be a little careful in meeting both threats.
9.Be3
The simplest way to make everything safe is often just to capture the attacking piece! Here 9.Nxe6 is a good example. In general, defending a piece can lead to passive positions and the possibility of a removal of the guard tactic! Moving the piece to a safe square, blocking, and counterattacking are the other three ways to make an attacked piece safe.
I often hear inexperienced players say that they did not want to trade off a piece because they did not want to “lose” that piece! If you make a fair trade, such as 9.Nxe6, then you are not “losing” that knight – you are trading it for something of equal value. Such an incorrect viewpoint can adversely affect your judgment because you may make a bad move to avoid “losing” something, when you are not losing anything at all. So think “fair trade,” not “lose!”
9...Ng6 10.0–0 (Finally!) 10...d5
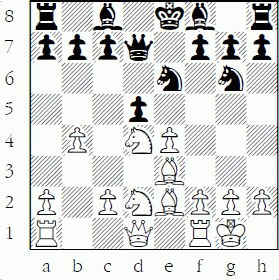
This move commences the first complex sequence of tactics in the game. A combination of basic motifs: a discovered attack on b4 by the bishop on f8, plus potential discovered pressure on d4 after a later ...dxe4; and counting, via the direct attack on e4. White needs to ensure that when he makes the b4-pawn safe, he also keeps the e4-pawn safe and the future discovered attack on d4 covered! That is a lot to ask an inexperienced player to see – and even more to ask him to meet it!
11.Bb5?
This would be a terrific counterattack, winning the queen for a bishop, if the pawn could not move to c6 – but since it can, the move is terrible. Little differences in a position can make a big difference in evaluation! Counterattacks are the most dangerous ways to defend against an attack.
White needed to defend the b4-pawn from the bishop on f8. Instead, he counterattacked the queen on d7 with the bishop. But ...c6 saves the queen and attacks the bishop on b5! So now the bishop and the pawn are both attacked. A very common mistake – I see it all the time! 11.exd5 is best, but even the simple 11.a3 is much better.
11...c6 12.Ba4
Another common mistake! This move is not bad – it is probably not any worse than 12.Be2, but inexperienced players often use bad logic: “My piece just came from e2, so it can’t be correct to return there!” But that would only make sense if 11.Bb5 was a good move. Instead, when you have to retreat after making a bad move, returning to the original square is frequently the best choice – but beginners often reject this. I once observed a player leave his piece en prise rather than make the only retreat back to where it had been!
12...Bxb4 13.Qf3??
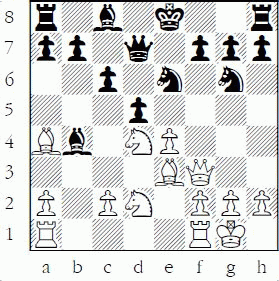
This is a “good” developing move, but a bad tactical error. Can you recognize a pattern similar to one we examined earlier that would win material for Black on the next move?
The problem is that the bishop on e3 is overworked. It cannot successfully guard both the knight at d4 and the knight at d2! When you are counting how many pieces are guarding something, any piece that is “removable” must not be counted! So Black can win material with 13...Nxd4!. This attacks the white queen and leaves White with little choice: 14.Bxd4 Bxd2 and Black wins a piece via removal of the guard! 13...Bxd2 is not as effective, since White can try 14.Nxe6 with some counterplay. (But not the automatic recapture 14.Bxd2? Nxd4.) Remember, when your opponent captures a piece, you usually have to take a piece back, but it does not always have to be on the same square!
13...dxe4?
Now White has two recaptures. Which one should he choose? Count carefully! Too many players play fast in this type of position; thinking which way they recapture does not matter, when it often matters more than most of your decisions in the rest of the game! Be very careful on moves involving checks, captures, and threats: one miscalculation could cause a loss.
14.Nxe4
14.Qxe4 is superior because the discovered attack on d4 has left two attackers on it (queen and knight), while after 14.Nxe4 White has only one defender, the bishop on e3. 14.Qxe4 also allows the queen to guard d4. Counting! Of course, there is more to this than just counting since White can play Nxe6 at some point, but hopefully you get the idea.
14...Nxd4
The queen on f3 is not safe.
15.Qd1?

White is in trouble, but he can greatly minimize the damage. The white queen is best made safe by capturing the attacker, which also lures the black queen into a pawn fork: 15.Bxd4 Qxd4 16.c3 winning back his piece. The immediate fork 15.c3 fails to 15...Nxf3+ winning the white queen.
Now it is White who has the counting threat. The queen’s retreat to d1 has now added an attacker to d4, so the black knight is not safe. 15.Qd1 is not anywhere as good as finding the fork, but at least it is a threat!
15...Qd5??
Throwing away almost all his advantage in one move! Black fails to realize that White is doing more than protecting his queen from being captured. Just because White is saving his queen does not mean the queen cannot also have a threat, and here it is to win the knight on d4.
16.Rb1??
Ouch! White does not capture the en prise knight, but instead attacks the bishop. Why attack a piece when you can get one for free? Another large counting error! On top of all that, 16.Qxd4 not only wins the knight, but also guards the attacked knight on e4.
16...Qc4??
Black should have played the simple 16...Qxe4 or even the unnecessarily tricky 16...Nf4.
17.Nd6+??
This is not only a counting error, but a very simple logic error as well. If this fork truly wins the queen, then likely White will be winning easily. Any time you see a move you think checkmates or wins easily, take some extra time to make sure you are correct! If you are, you won’t need a lot of extra time, but if you are not, you want to know before you make the move!
17...Kd7??
Black is probably in shock and believes that his lower rated opponent has won the queen. If Black stopped to find the best way out of check, he would probably have found 17...Bxd6. Never touch your king before looking to see if there is a better way to get out of check especially when you can capture the checking piece for free!
18.Nxc4
You were expecting that! White went on to win easily. Yes, he did!
More Counting Examples
The following example shows that a pinned piece affects counting: 1.e4 c5 2.Nf3 d6 3.Nc3 Nf6 4.Bc4 Qa5 5.0–0 Ng8 6.d3 Bg4 7.Bf4 Nd7 Now, is 8.e5 safe?
White to play
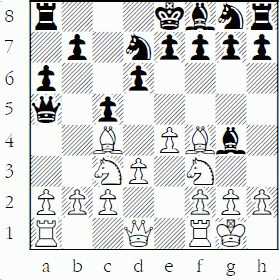
The answer is no: 8.e5? dxe5 9.Bxe5?? Nxe5 and Black wins a piece as the knight is pinned. This shows that pinned pieces often cannot be counted as defenders.
In the next diagram, a relatively pinned piece (not pinned to a king) moves with advantage: 1.e4 d6 2.d4 Nf6 3.Nc3 g6 4.Bg5 Bg7 5.f4 h6 6.e5 hxg5 7.exf6 Bxf6 8.Ne4 e5 9.fxe5 dxe5 10.dxe5 Qxd1+ 11.Rxd1 Bxe5 12.Nf3 Bg4
White to play and win after 12...Bg4
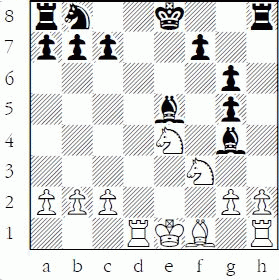
13.Nxe5 Bxd1 14.Kxd1 White wins two bishops for a rook – a relatively large material advantage.
Below, Black incorrectly counterattacks instead of just moving his piece to safety, a common mistake: 1.d4 d5 2.Nf3 Nc6 3.c4 e6 4.Nc3 Nf6 5.Bg5 Be7 6.Ne5 0–0 7.cxd5 exd5 8.Nxc6 bxc6 9.e3 Bg4 10.Be2 h6?:
White to play and win
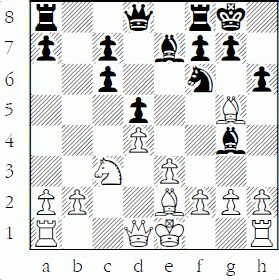
This is a typical counting error. 11.Bxf6 (not 11.Bxg4? hxg5) 11...Bxe2 12.Bxe7 Qxe7 13.Qxe2 and White wins a piece.
Pinned pieces often cannot be counted as defenders.
1-1 Black to play and win
1-2 White to play and win
1-3 Black to play and save a piece
1-4 Black to play; is ...Ne4 safe?

1-5 White to play and win

1-6 Can Black play 1...Nxe4 2.Nxe4 d5 and win back his piece?
1-7 Can White win the d-pawn?

1-8 White to play; is Bxb5 safe?
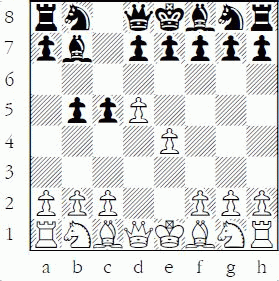
1-9 White to play and win a pawn
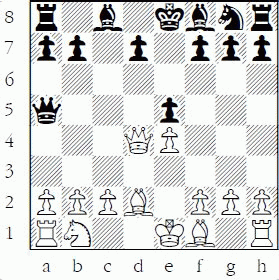
1-10 White to play and win
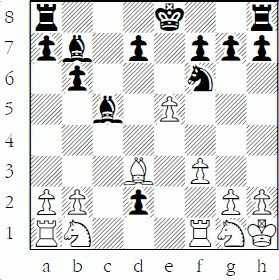
1-11 Black to play; is ...Ng4 good?

1-12 White to play and win a pawn
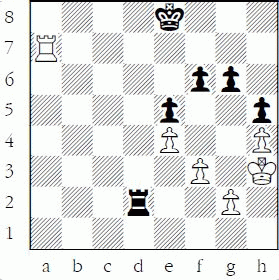
1-13 White to play and win
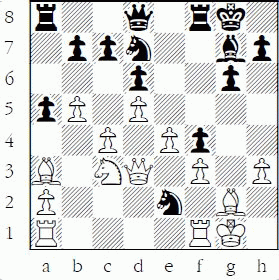
1-14 Black to play and win a pawn
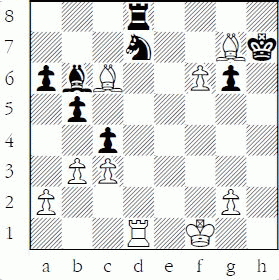
1-15 White to play and win

1-16 White to play and win a pawn
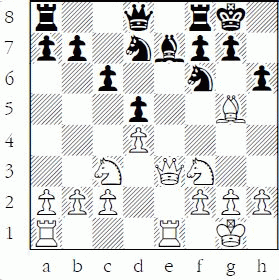
1-17 White to play and stay ahead material
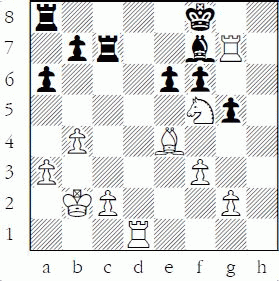
1-18 Black to play and win a pawn

1-19 Black to play and win
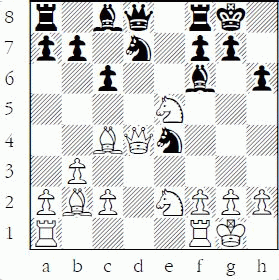
1-20 Black to play and win
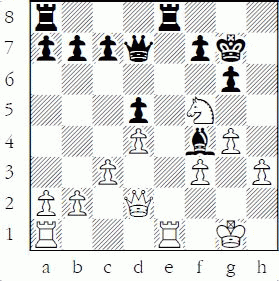
1-21 Black to play and win

1-22 White to play and save a piece
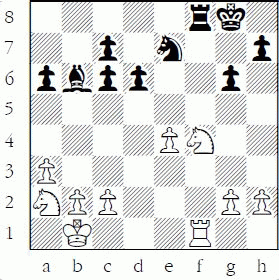
1-23 Can White win a piece?
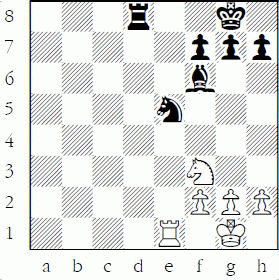
1-24 Black to play and win

1-1: 1...Bxf3 2.Qxf3 Rxg7 A typical easy counting problem. Black trades off his attacked piece before he wins the hanging bishop on g7.
1-2: 1.Nxd4 Bxd1 2.Nb3 Be2 3. Re1 wins a piece.
1-3: 1...Ke6 is necessary to save the knight on d5 and maintain equal chances in this famous “Fried Liver” position. Retreating the king to “safety” and returning the knight is just hopeless, and a common beginner mistake.
1-4: Yes. 2.Bxe7 Qxe7 or 2.Bxe4 Bxg5. And 2.Nxe4? dxe4 3.Bxe7 Qxe7 wins for Black.
1-5: 1.Bxd7 But not the “cute” 1.Rxd4 Nb6!. 1...Qxe5 1...dxe3 2.Qxe4 wins a piece. 2.Bd2 leaves White ahead a piece.
1-6: No. This “center fork trick” does not work with a bishop on c5! 1...Nxe4 2.Nxe4 d5 3.Nxc5.
1-7: No. 1.Nxd4 Bxd4 2.Rxd4 Qxd4 3.Qxd4 Re1#.
1-8: Yes. 1.Bxb5 Qa5+ 2.Nc3 guards the bishop and remains a pawn ahead.
1-9: The desperado queen sacrifice 1.Qxd7+ Bxd7 2.Bxa5 wins a pawn.
1-10: The pawn on d2 is not going anywhere: 1.exf6 wins the knight. In the actual game White panicked and played the hasty 1.Nxd2??, allowing Black to save the piece with 1...Nd5.
1-11: No. White wins two pieces for the rook. 1...Ng4? 2.fxg4 Bxg1 3.Kxg1.
1-12: 1.Rg7 and if Black tries to trap the rook, White escapes: 1...Kf8 2.Rxg6 Kf7 3.Rh6 Kg7 4.Rxh5 Kg6 5.Rh8 Kg7 6.Rb8.
1-13: 1.Nxe2 Not capturing is an unbelievably big counting mistake 1...Bxa12.Rxa1 and White is ahead two pieces for a rook.
1-14: 1...Nxf6 2.Rxd8 Bxd8 and Black holds everything while winning back the pawn he was down.
1-15: 1.Ne7+ Qxe7 2.fxe7 wins the house!
1-16: 1.Bxh6 1.Qxe7 hxg5 2.Qxd8 Raxd8 3.Nxg5 is almost as good, and also counts as correct! But not 1.Bxf6? Bxf6, when White has nothing. 1...gxh6 If 1...Ng4 2.Qxe7 and if 1...Re8 2.Bg5. 2.Qxe7 and White is ahead a pawn.
1-17: 1.Rxf7+ Rxf7 2.Nd6 and White remains ahead two pieces for a rook.
1-18: 1...Ng4 2.Qe2 Qc7 wins the e-pawn.
1-19: 1...Bxe5 (skewer!) 2.Qxe4 Bxb2 wins a piece.
1-20: 1...Qxf5 2.gxf5 Bxd2 and Black ends up a piece ahead.
1-21: 1...Rxc1 Of course not 1...Bxd5? 2.Rxc8. 2.Rxc1 Bxd5 wins a piece for Black.
1-22: 1.Rf3 If instead 1.Rf2?? Bxf2. Other moves allow 1...g5 or 1...Rxf4.
1-23: No. If 1.Nxe5 Bxe5 2.Rxe5?? Rd1+ 3.Re1 Rxe1#.
1-24: 1...Qxb1+ 2.Nxb1 Nxd5 leaves Black a rook ahead. 1...Nxc2+? 2.Kd1 is good for White.