Chapter 10
Mortgage Dollar Roll
The future's uncertain but the end is always near.
Jim Morrison
The mortgage dollar roll is a financing mechanism used in the agency mortgage-backed securities market. This chapter introduces the reader the mechanics of the dollar roll. Break-even and financing analyses, and the risks associated with implementing a dollar roll program are outlined. The dollar roll provides investors, mortgage originators, and dealers with a flexible means to hedge and finance their respective residential mortgage positions:
- For investors, the dollar roll represents 100% collateralized borrowing at advantageous rates.
- Mortgage originators are able to sell their production forward in the -to be announced-, or (TBA), market due to the liquidity of the dollar roll market.
- Dealers are able to hedge or cover their positions efficiently due to the depth and liquidity of the market.
The low cost of funds and flexibility afforded mortgage market participants entails additional risks. Managing these risks is critical to implementing a successful mortgage dollar roll program.
The dollar roll is a specialized type of collateralized borrowing unique to the agency mortgage-backed securities market and allows for a 100% advance rate against a pool of agency MBS. It evolved due to the dealers' need to borrow these securities to cover short positions and mortgage originators' need to hedge their origination pipeline (long positions) by selling forward. The dollar roll is named such because dealers are said to either roll in collateral (borrowing) or roll out collateral (returning).
The mortgage dollar roll is similar in nature to a mortgage repurchase (repo) agreement in that it represents a loan collateralized by mortgage-backed securities and calls for the simultaneous sale and purchase of the MBS at execution. However, it is materially different from a repurchase agreement in two ways:
- The dealer is not required to return the identical securities rolled out by the investor. Instead, the dealer need only return substantially similar securities. Meeting this condition is important from an accounting standpoint as set forth in FAS 140. Failure to meet the FAS 140 standard would result in a dollar roll transaction being accounted for as a sale rather than a financing.1
- Unlike a traditional repurchase agreement, the investor surrenders the right to the bond cash flows. As a result, the forward settlement price is lower than the initial settlement price. The drop in price compensates the investor for the forgone interest and principal, which is another feature that differentiates a dollar roll transaction from a traditional repurchase agreement.
Figure 10.1 illustrates the mechanics of the dollar roll and the interaction between MBS pass-through securities and real estate mortgage investment conduits (REMICs). A dealer may roll in MBS securities to deliver against a short position to a REMIC execution—the dealer is short MBS against a long REMIC execution:
- With respect to a REMIC execution, assume a dealer is settling the REMIC in the next month. If the dealer is unable to purchase the collateral required to settle the REMIC, the dealer may roll in collateral. The roll-in is accomplished by bidding up the front month roll to the point where it is more favorable for the investor to roll out collateral to the dealer rather than hold it.
- In the case of a short position to an MBS investor, a dealer may simultaneously roll in and roll out collateral.

Figure 10.1 Mechanics of the Mortgage Dollar Roll
Through the dollar roll market, dealers are able to obtain the collateral needed to settle REMIC execution while also hedging their MBS pass-through inventory. The MBS investor is able to access favorable advance rates and financing costs.
10.1 Evaluating the Dollar Roll
Recall from above, unlike a repurchase agreement where the right to the security's cash flows remains with the party that repos (rolls) out the collateral, the dealer or counterparty that repos (rolls) in the collateral retains the coupon interest and any principal paid during the term of the dollar roll. Consequently, the computation of the financing cost of the dollar roll is not as straightforward as that of a typical repurchase agreement.
In a dollar roll transaction, the agreed upon repurchase price is lower than the sale price. At first blush, this pricing may seem counterintuitive; however, since the rights to the mortgage security's cash flows, both principal and interest, are transferred to the party rolling in the collateral, the party rolling out the collateral must make up the difference between the carry on the MBS and the short-term financing rate. As a result, the repurchase price is less than the sale price—this difference is commonly referred to as the drop. The following inputs are required to calculate the financing cost:
- Sale or roll-out price and the repurchase or roll-in price
- Coupon payment
- Amounts of both the scheduled and prepaid principal received
- Characteristics of the collateral that is rolled in
- Timing of the settlement dates, i.e., their impact on accrued interest
The dollar roll is a repurchase agreement and reflects an implied cost of funds that is calculated from the drop. Thus, by the law of similarity, for a given cost of funds there is also an implied drop. The implied drop is referred to as the breakeven drop and is based on the investor's alternative financing cost. The upcoming section reviews the framework for analyzing the breakeven drop.
Consider a 5.5% MBS originated with a first payment date of October 1, 2011. Furthermore, suppose on January 13, 2013, an MBS investor is evaluating a long position in this pass-through security.
- The gross WAC (GWac) of the pool is 6.10%.
- The current weighted-average maturity (WAM) is 344 months.
- The recent one-, three-, and six-month prepayment rates (CPR) are: 28, 25, and 21, respectively.
- The current price for January settlement is quoted at
 .
. - The investor's alternative financing cost is 0.31%.
- The assumed prepayment rate is 30% CPR.
- The investor roll-out settlement date is January 14, 2013.
- The investor roll-in settlement date is February 12, 2013.
10.1.1 The Breakeven Drop Rate
Given the previous information, the investor must make a decision. She may either finance the position via the dollar roll market or seek an alternative financing source at 0.31%. Table 10.1 illustrates the investor's computation of the breakeven drop rate, which is the drop price at which she will-break even-between financing her position in the dollar roll versus her alternative financing option. The calculation is as follows:
Table 10.1 Breakven Drop Calculation
| Beginning Market Value | |||
| Principal Proceeds | $ | 1,075,000 | 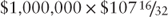 |
| Accrued Interest | $ | 1,986 | 13 days accrued interest @ 5.50% |
| ① Market Value | $ | 1,076,986 | Total proceeds on the roll-out date |
| Future Value—Pmts. Received | |||
| Coupon Income Received | $ | 4,583 | Interest earned @ 5.50% based on 30/360 |
| Scheduled Principal Received | $ | 1,219 | Scheduled principal paid |
| Prepaid Principal Received | $ | 29,250 | Prepaid principal received @ 30 CPR |
| Total Payments Received | $ | 35,052 | Expected payments (remittance date) |
| ② Disc. Value of the Carry | $ | 35,048 | Present value of the payments received assuming the alternate financing rate (0.31%) and using actual day count (13 days)—act/360—on the roll-in date. |
| Remaining Principal Balance | $ | 969,531 | Remaining current balance |
| Principal Proceeds | $ | 1,042,246 | Remaining balance  $ $ |
| Accrued Interest | $ | 1,925 | 13 days of accrued interest |
| Roll-in Proceeds | $ | 1,042,245 | Roll-in proceeds |
| Future Value of Principal and Carry | $ | 1,079,220 | Total amount financed |
| Less Financing Cost | $ | 268 | Actual days between roll-out date and roll-in date based on actual/360 day count |
| ③ Future Value | $ | 1,078,951 | Principal and carry less financing costs |
| Future Value | $ | 1,078,951 | |
| Less Market Value | $ | 1,076,989 | |
| Implied Value of the Drop | $ | 1,962 | |
④ Breakeven Drop ( ) ) |
6.5 | ($1,852 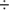 $969,531) $969,531)  32 32 |
|
- ① The investor computes the proceeds on the roll-out date.
- The principal proceeds is the current face amount:
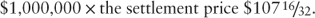
- The accrued interest is calculated on a 30/360 basis:

- The total market value of the the position is $1,076,986.
- The principal proceeds is the current face amount:
- ② The investor computes the discounted value of the carry on the roll-in date.
- Calculate the interest paid on the remittance date based on a 30/360 payment date. The MBS pays principal and interest with a 24-day delay. Thus, remittance is the 25th day of the month.
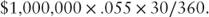
- Calculate the scheduled principal paid by the borrowers.
- After giving credit to the scheduled principal paid, the investor calculates the expected prepaid principal based her prepayment assumption used to value the dollar roll—in this case, 30 CPR.
- Summing the above items, the investor is able to determine the expected total payments received on the remittance date, which is the carry earned by the investor.
- Finally, the roll-in settlement date occurs on the 12th day of the month, 13 days prior to the remittance date. Thus, the investor must discount the carry by the alternative financing rate using the actual/360 day count convention.
- Calculate the interest paid on the remittance date based on a 30/360 payment date. The MBS pays principal and interest with a 24-day delay. Thus, remittance is the 25th day of the month.
- ③ The investor calculates the future value at the roll-in date.
- The principal proceeds at the roll-in date are based on the settlement price.

At first glance, this approach may seem counterintuitive because one might suspect that she should use the roll-out price. She uses the settlement (roll-in) price because she is solving for the breakeven drop, which is the compensation for the forgone principal and interest.
- The accrued interest is calculated on a 30/360 basis:

- The roll-in proceeds is the sum of the principal and accrued interest
- The future value of the carry is equal to the sum of the roll-in proceeds plus the discounted value of the carry
- The financing cost represents the cost to finance the future value of the carry between the roll-out date and the roll-in date. The financing cost is based on the actual/360 day count.
- The principal proceeds at the roll-in date are based on the settlement price.
- ④ Finally, she calculates the implied value of the drop.
- Subtract the future value of the principal and carry at the roll-in date from the market value at roll-out date.
- Divide the above by the remaining balance at the roll-in date $969,531.
- Finally, multiply the quotient by 32—the product is the drop in thirty-seconds. The breakeven drop is
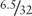 .
.
The breakeven drop is $0– . Given that the quoted ($
. Given that the quoted ($ ) is less than the breakeven drop, the investor would be better off holding her position given alternative financing available (one-month LIBOR) rather than financing her position in the one-month dollar roll market.
) is less than the breakeven drop, the investor would be better off holding her position given alternative financing available (one-month LIBOR) rather than financing her position in the one-month dollar roll market.
10.1.2 The Implied Cost of Funds
Table 10.2 Implied Cost of Funds
| Beginning Market Value | |||
| Principal Proceeds | $ | 1,075,000 |  |
| Accrued Interest | $ | 1,986 | 13 days accrued interest @ 5.50% |
| ① Market Value | $ | 1,076,986 | Total proceeds on the roll-out date |
| Future Value - Pmts. Received | |||
| Coupon Income Received | $ | 4,583 | Interest earned @ 5.50% based on 30/360 |
| Scheduled Principal Received | $ | 1,219 | Scheduled principal paid |
| Prepaid Principal Received | $ | 29,250 | Prepaid Principal Received @ 30 CPR |
| Total Payments Received | $ | 35,052 | Expected payments (remittance date) |
| ② Disc. Value of the Carry | $ | 35,048 | Present value of the payments received assuming the alternate financing rate (0.31%) and using actual day count (13 days)—act/360—on the roll-in date. |
| Remaining Principal Balance | $ | 969,531 | Remaining current balance |
| Principal Proceeds | $ | 1,040,731 | Remaining balance  $ $ |
| Accrued Interest | $ | 1,925 | 13 days of accrued interest |
| Roll-in Proceeds | $ | 1,042,656 | Roll-in proceeds |
| Future Value of Principal and Carry | $ | 1,077,709 | |
| Future Value | $ | 1,077,709 | |
| Less Market Value | $ | 1,076,986 | |
| Implied Cost of Financing | $ | 723 | |
| ④ Implied Cost of Funds | 0.81% | ($726  $1,076,986) $1,076,986)  12 12 |
|
The dollar roll, by market convention, is quoted as a drop. However, in practice most investors do not evaluate the dollar roll via the implied drop. Rather, they prefer to evaluate the dollar with respect to its implied financing cost. This section illustrates the analysis by applying the actual drop ($ ) to compute the implied financing cost. Table 10.2 illustrates that, for the most part, the analysis is the same as that used to calculate the implied drop. The difference is the investor uses the quoted drop, or forward price, to value the remaining principal balance at the roll-in date.
) to compute the implied financing cost. Table 10.2 illustrates that, for the most part, the analysis is the same as that used to calculate the implied drop. The difference is the investor uses the quoted drop, or forward price, to value the remaining principal balance at the roll-in date.
Simply stated, if the implied financing cost is below that of the investor's alternative financing option, in this case 31 basis points, then the dollar roll represents a superior financing choice. In the example presented in Table 10.2, the implied financing cost is 81 basis points.
The implied cost of funds is also referred to as the breakeven financing rate because the investor must invest the borrowed funds for the term of the dollar roll. If her reinvestment rate is equal to the cost of funds, then there is no arbitrage for her and she will break even versus holding the collateral.
10.1.3 Hold-versus-Roll Analysis
The hold-versus-roll analysis presented in Table 10.3 is based on the same inputs as those used in the calculation of the breakeven drop and implied cost of funds. The only additional input to the analysis is the investor's expected reinvestment rate. Building on the previous analysis, the investor's reinvestment rate is 0.31%. For the MBS investor, the hold-versus-roll analysis is straight forward.
- If the reinvestment rate is greater than the dollar roll's implied cost of funds the investor faces a positive economic incentive to roll the collateral in the portfolio.
- If the reinvestment rate is equal to the dollar roll's implied cost of funds the investor is indifferent, economically speaking, to holding versus rolling the collateral.
- If the reinvestment rate is below the implied cost of funds, the investor will choose to hold the collateral.
Table 10.3 Hold-versus-Roll Analysis
| Roll | Hold | ||||
| Beginning Market Value | $ | 1,075,000 | Future Value of Pmts. | $ | 35,052 |
| Accrued Interest | Remaining Principal: | ||||
13 days  5.50% 5.50% |
$ | 1,986 | $969,531  $ $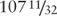 |
$ | 1,040,731 |
| Proceeds: | $ | 1,076,986 | Proceeds: | $ | 1,075,783 |
| Reinvestment Income | $ | Accrued Interest | |||
29 days  0.31% 0.31% |
$ | 269 | 12 days  5.50% 5.50% |
$ | 1,777 |
| Future Value: | $ | 1,077,255 | Future Value: | $ | 1,077,709 |
| Dollar Advantage: | $ | 454 | |||
| Basis Points (Annualized) | 0.50% | ||||
The dollar advantage of the hold-versus-roll analysis is often quoted as an annualized basis point advantage. In this case, the advantage to the investor of holding versus rolling the collateral is 0.50% on an annualized basis. The analysis suggests that by holding the collateral the investor gains 0.50% on an annualized basis over rolling the collateral.
10.2 Risk Associated with the Dollar Roll
The hold-versus-roll analysis above is predicted on the assumption that both the investor and the dealer return exactly the same notional amount and deliver a substantially identical security that would command the same price. However, there are risks associated with the dollar roll that must be factored into the hold-versus-roll analysis:
- Prepayment risk: the risk that the realized prepayment rate will be significantly different than that used to price the dollar roll.
- Delivery risk: the risk that either party may over- or underdeliver the agreed upon notional amount.
- Adverse selection risk: the risk that neither party is required to return the same securities. Instead, each party is obligated to return substantially similar securities.
10.2.1 Prepayment Risk
The prepayment risk of the dollar roll is attributable to its unique nature. Recall, the party rolling out the collateral does not retain the right to its cash flows. As a result, the party rolling in the collateral accepts the prepayment risk of the roll transaction. The investor's cost of funds is determined by the difference between the actual prepayment rate and the prepayment rate agreed on under the terms of the dollar roll agreement.
- In the case of a premium mortgage, a slower prepayment rate than that agreed increases the borrower's cost of funds because a slower prepayment rate favors the party rolling in the collateral. Conversely, a faster prepayment rate than that agreed reduces the borrower's cost of funds because a faster prepayment rate will favor the party rolling out the collateral.
- In the case of a discount mortgage the opposite holds. A faster prepayment rate than that agreed increases the borrower's cost of funds because a faster prepayment rate favors the party rolling in the collateral. Conversely, a slower prepayment rate than that agreed reduces the borrower's cost of funds because a slower prepayment rate favors the party rolling out the collateral.
- Finally, the closer the collateral price to par, the lower the overall sensitivity of the dollar roll's cost of funds to the realized prepayment rate.
10.2.2 Delivery Risk
The dollar roll allows a 1.0% settlement variance, which permits either party to over- or underdeliver the agreed notional amount, creating a delivery option for both parties to the transaction. Essentially, each party owns a put option to the other.
Suppose an investor enters into a roll-in transaction as presented above. The dealer's roll-out price is $107-16/32 to settle on January 14, 2013. Furthermore, assume between the trade date—January 10, 2013—and at the settlement date the price increases $0-5/32 to $107-21/32. The investor will underdeliver to the dealer versus the roll. Conversely, if the price were to decline by a similar amount, the investor would overdeliver to the dealer.
The dealer also owns a delivery option on the roll-out date. The roll-out settlement date is February 12, 2013, and the drop is $0-5/32 for a settlement price of $107-11/32. Assume the price declines to $107-06/32. In this case, the dealer would overdeliver by 1.0% to the investor. Conversely, if the price increases the dealer would underdeliver to the investor.
10.2.3 Adverse Selection Risk
Adverse selection risk arises because neither party to the roll agreement is obligated to return the same securities. Rather, as mentioned above, each party is obligated to return substantially similar securities.
- For example, in the case of a discount pool, desirable characteristics include such things as a shorter weighted average maturity and faster prepayment rates. Thus, one would deliver to the roll a discount pool with a longer average life and slower prepayments.
- For a premium pool, desirable characteristics include a longer weighted average maturity and slower prepayment rates. Thus, one would deliver to the roll a premium pool with a shorter average life and faster prepayments.
- It is in neither party's best interest to deliver pools with better-than-average characteristics. Rather, both parties are motivated to deliver below-average pools into the dollar roll.
Finally, the risk of adverse selection may be managed by the investor via pool stipulations (stips). For example, the investor may stipulate an acceptable range for a weighted-average coupon, weighted average loan age as well as other loan or borrower characteristics. However, stipulations require adjustments to the drop. These stipulations usually result in a lower absolute drop.
This chapter provides a framework for analyzing the mortgage dollar roll. The dollar roll provides a flexible financing mechanism for investors, dealers, and mortgage originator and servicers to manage and finance their positions at a competitive cost of funds. The low cost of funds and flexibility afforded mortgage market participants by the dollar roll comes with additional risks: prepayment, delivery, and adverse selection.